栅格数据结构是以规则栅格阵列来表示空间对象的数据结构。在这个阵列中，每个栅格单元上的数值表示空间对象的属性特征。如空间对象的类型、等级等等。但每个栅格单元只能存在一个值。

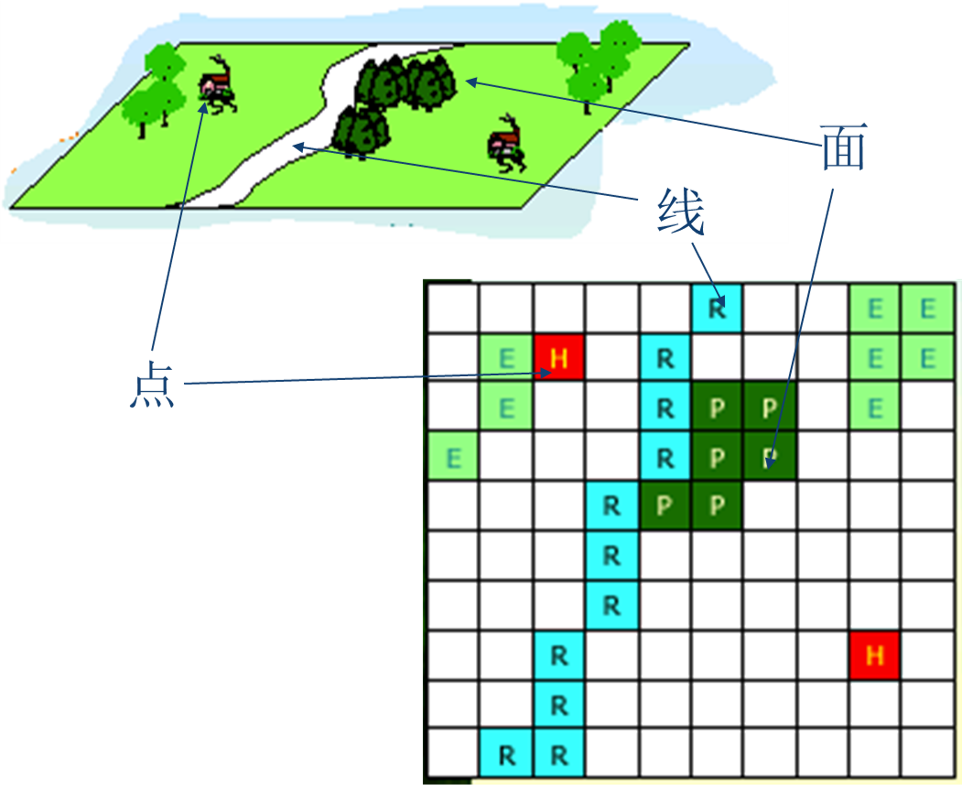
栅格数据结构表示的地表是不连续的，是量化和近似离散的数据。因此，在栅格数据结构中，地理空间被分成相互邻接、规则排列的栅格单元，一个栅格单元对应于小块地理范围。在这种数据结构中，点用一个栅格单元表示；线状地物则用沿线走向的一组相邻栅格单元表示，在线上，每个栅格单元最多只有两个相邻单元；而面或区域用记录区域属性的相邻栅格单元的集合表示，每个栅格单元可有多于两个的相邻单元同属一个区域。

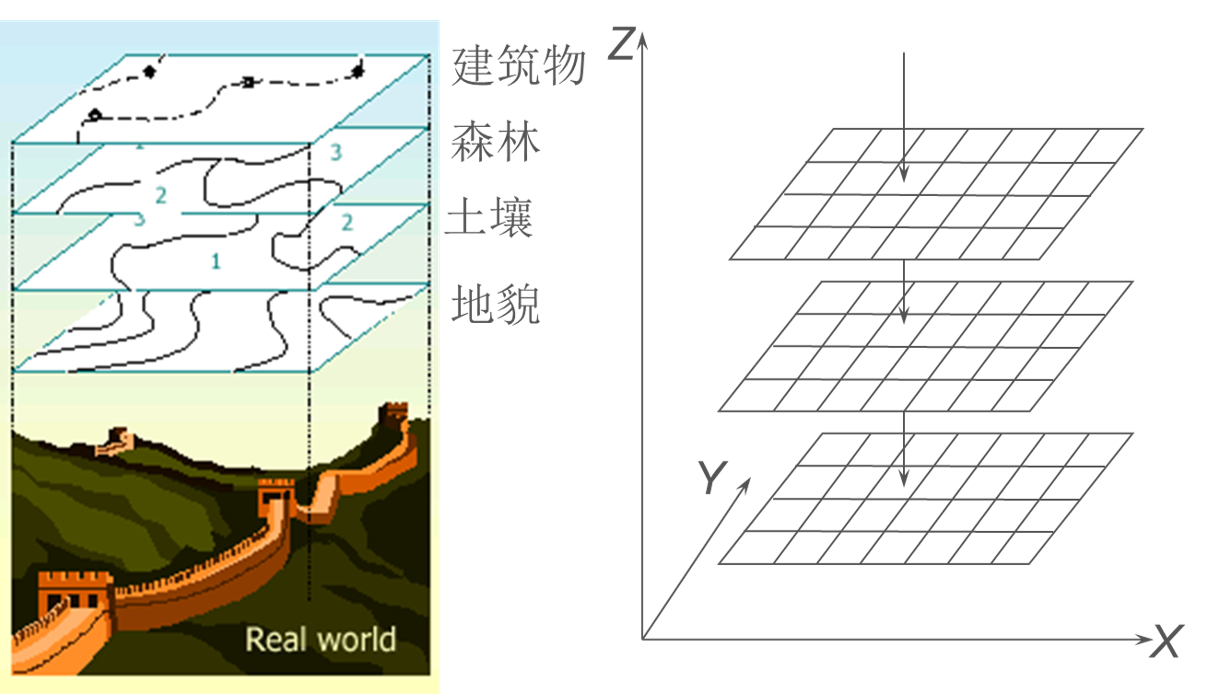
栅格数据结构的显著特点是：属性明显，定位隐含，即数据直接记录属性的指针或属性本身，而所在位置则根据行列号转换为相应的坐标给出，也就是说定位是根据数据在数据集中的位置得到的。

相对于矢量数据，栅格数据有其自身的优缺点：优点是其数据结构简单、数学模拟方便而缺点也很明显，这就是，数据量大、难以建立实体间的拓扑关系，如果通过改变分辨率而减少数据量时，精度和信息量同时受损等。

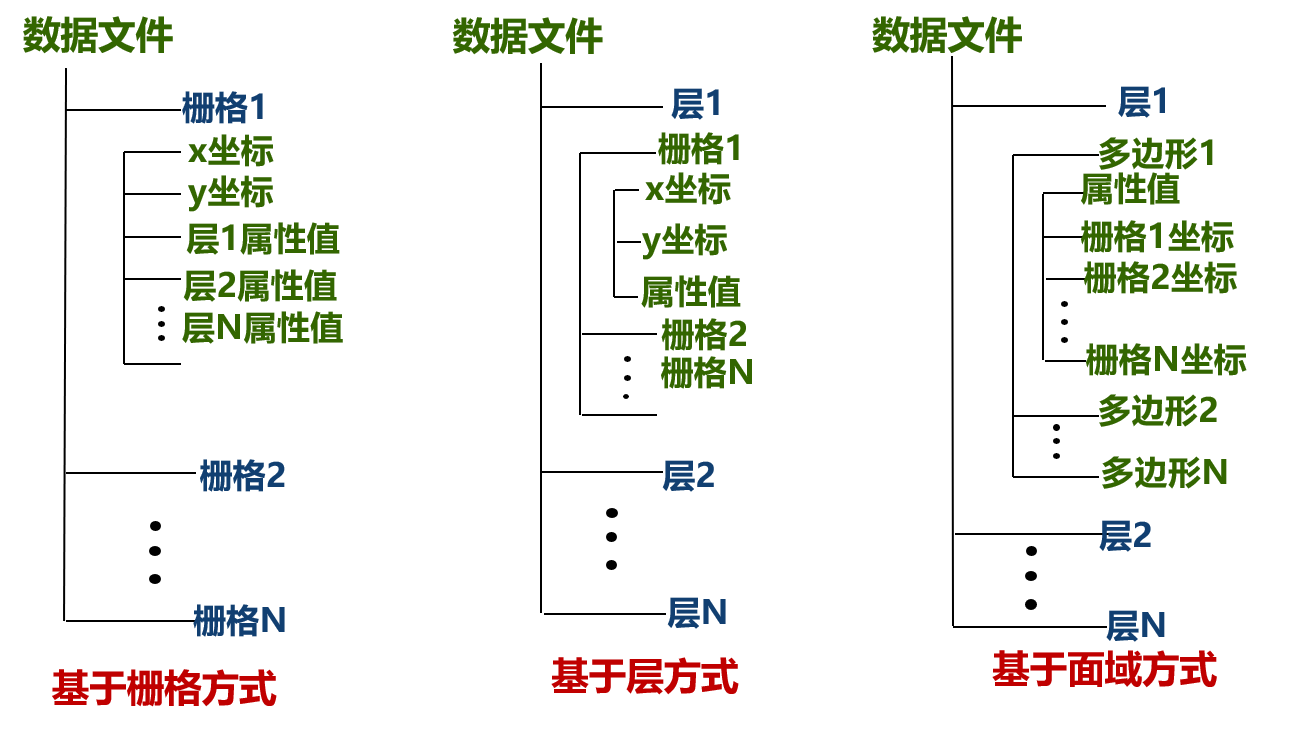
栅格数据单元值确定有中心点法、面积占优法、重要性法以及百分比法。

栅格数据的存储方式较多，有最简单的完全栅格数据结构，也有为了数据压缩的行程编码、四叉树等，更有从单一尺度到多尺度的栅格金字塔。

完全栅格数据结构（也称编码）将栅格看作一个数据矩阵，逐行逐个记录栅格单元的值。可以每行都从左到右，也可奇数行从左到右而偶数行从右到左，或者采用其他特殊的方法。这是最简单最直接的一种栅格编码方法。通常这种编码为栅格文件或格网文件。它不采用任何压缩数据的处理，因此是最直观、最基本的栅格数据组织方式。

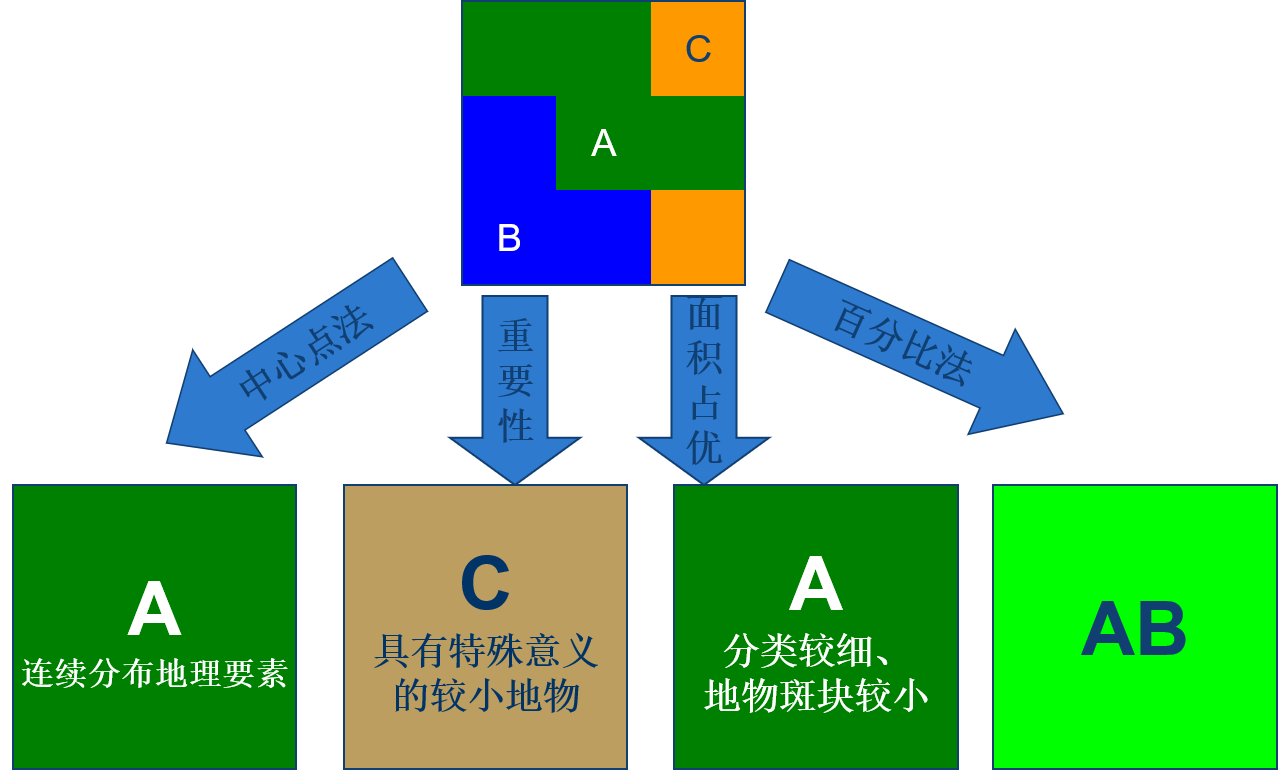
完全栅格数据的组织有三种基本方式：基于象元、基于层和基于面域的方式。

基于像元的方式是以像元为独立存储单元，每一个象元对应一条记录，每条记录中的记录内容包括象元坐标及其各层属性值的编码；由于这种方式对各层对应象元的坐标只需存储一次所以节省了许多存储坐标的空间。同时，这种方式数据组织方式简单明了，便于数据扩充和修改，但在进行属性查询和面域边界提取时速度则较慢；

第二种是基于层的方式，这种方式以层为存储基础，层中又以象元为序记录其坐标和对应该层的属性值。所以便于进行属性查询，但每个象元的坐标均要重复存储，浪费了存储空间；

第三种是基于面域的组织方式。这种方式也以层作为存储基础，在层中再以面域为单元进行记录，记录的内容包括面域编号、面域对应该层的属性值编码和面域中所有栅格单元的坐标；而同一属性的多个相邻象元只需记录一次属性值这种方式虽然便于面域边界提取，但在不同层中象元的坐标还是要多次存储。

完全栅格数据结构最直观最基本的栅格数据组织方式，它所有栅格都存储下来的方式，然而，对于一幅栅格图像，常常有行（或列）方向上相邻的若干点具有相同的属性代码，因而可采取某种方法压缩那些重复的记录内容。

第一种压缩栅格数据结构是游程长度编码，也称行程编码。其编码方案是，只在各行（或列）数据值发生变化时,才依次记录该值以及相同值重复的个数，从而实现数据的压缩，并实现数据的组织。

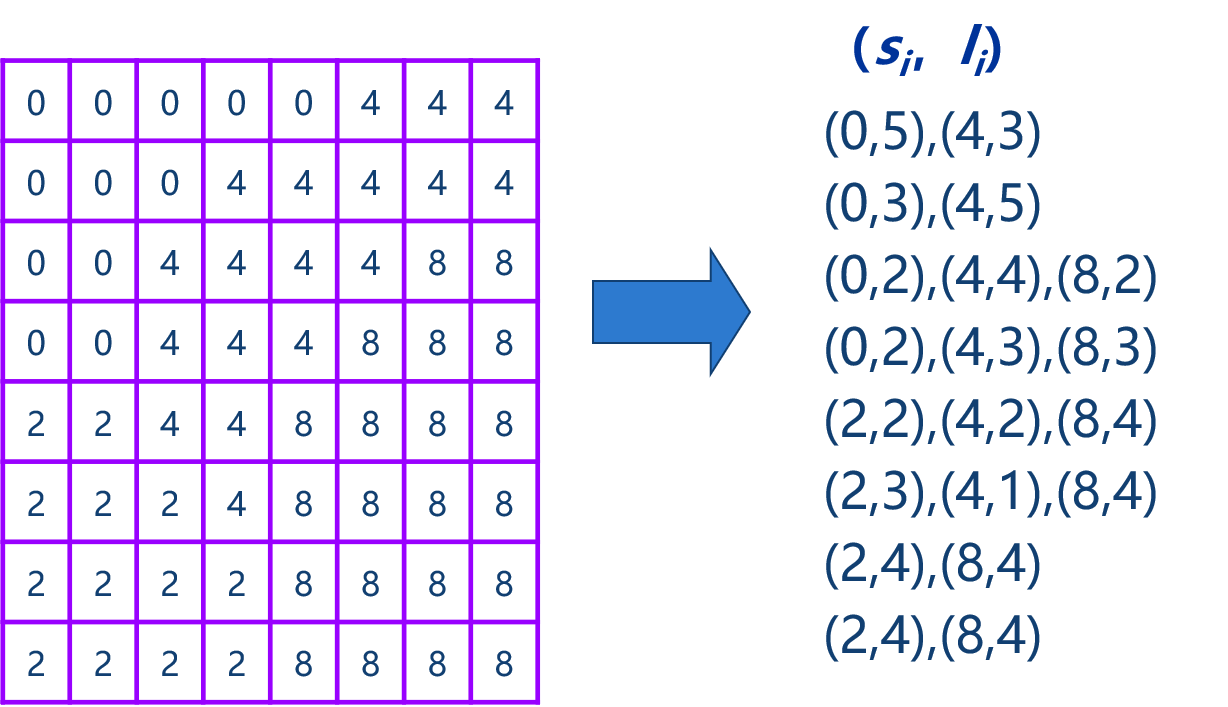
经编码后，原始栅格数据阵列转换为（属性值，行程）数据对，行程即为相同值重复的个数。游程长度编码是一种栅格数据无损压缩的重要方法。其压缩比的大小与图的复杂程度成反比的，在变化多的部分，游程数就多，变化少的部分游程数就少，原始栅格类型越简单，压缩效率就越高。因此这种数据结构最适宜于类型面积较大的专题要素、遥感图像的分类结构，而不适合于类型连续变化或类型分散的分类图。

第二种压缩栅格数据结构是四叉树数据结构。它的思路是将一幅栅格数据层或图像等分为四部分，逐块检查其格网属性值（或灰度）；如果某个子区的所有格网值都具有相同的值，则这个子区就不再继续分割，否则还要把这个子区再分割成四个子区；这样依次地分割，直到每个子块都只含有相同的属性值或灰度为止。这样分割下去就是一棵倒立的四叉树。为了保证四叉树能不断的分解下去，就要求栅格数据的栅格单元数必须满足，n为极限分割次数，n+1 是四叉树的最大高度或最大层数。对于非标准尺寸的图像，则需首先通过增加背景的方法将栅格数据扩充为个单元，对不足的部分以0 补足，在建树时，对于补足部分生成的叶结点不存储，这样存储量并不会增加。

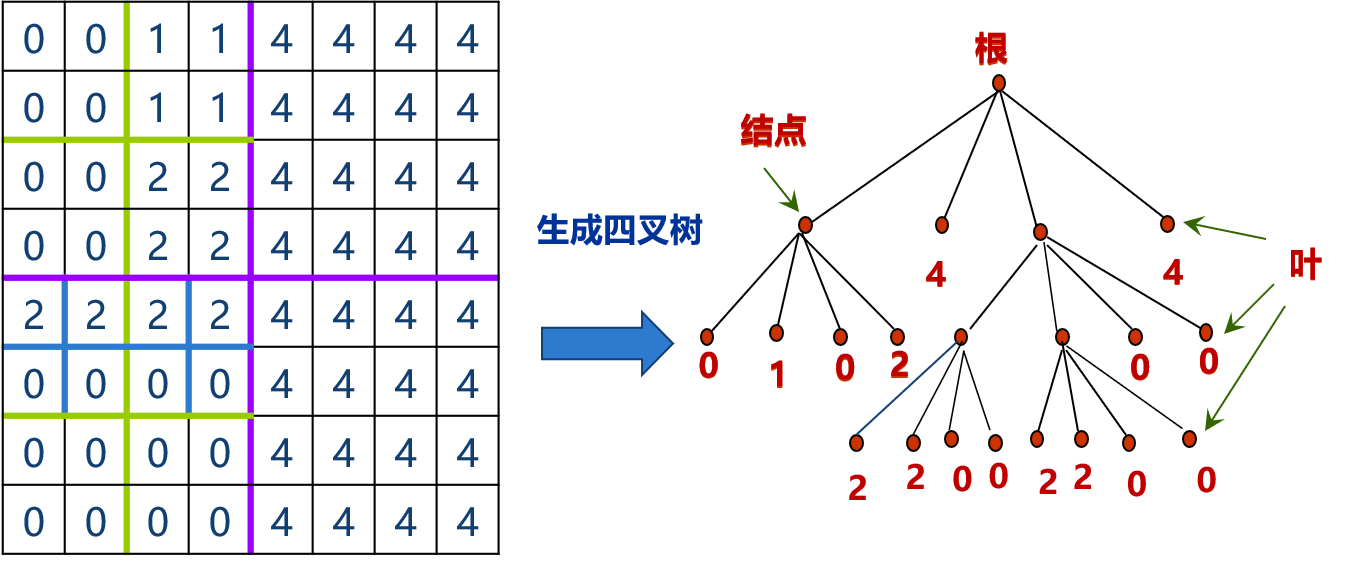
四叉树结构按其编码的方法不同又分为常规四叉树和线性四叉树。常规四叉树除了记录叶结点之外，还要记录中间结点。结点之间借助指针联系，每个结点需要用六个量表达：包括四个叶结点指针，一个父结点指针和一个结点的属性或灰度值。这些指针不仅增加了数据贮存量，而且增加了操作的复杂性。常规四叉树主要在数据索引和图幅索引等方面应用。

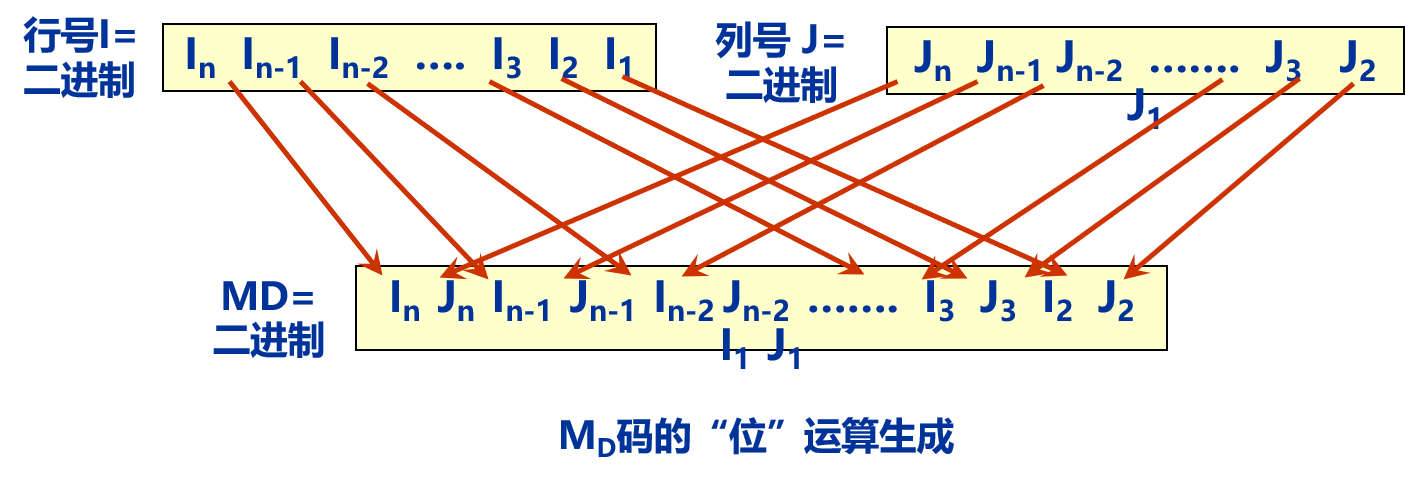
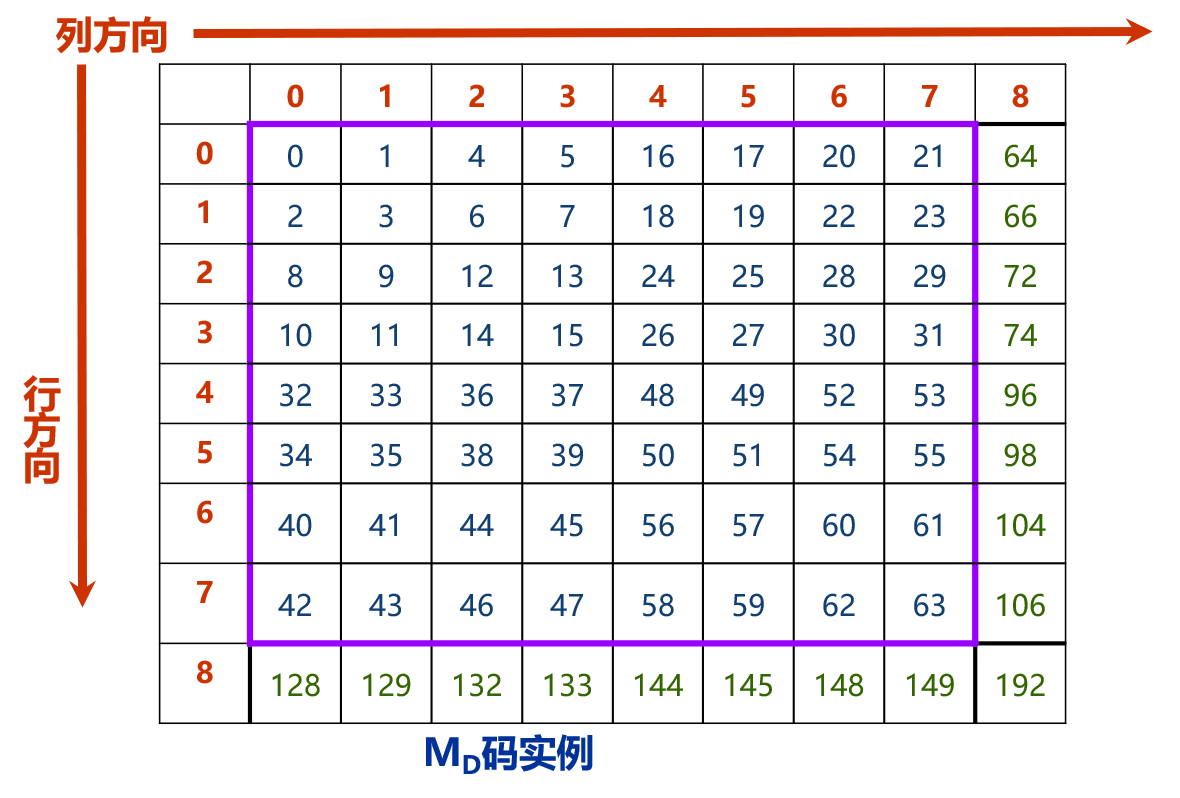
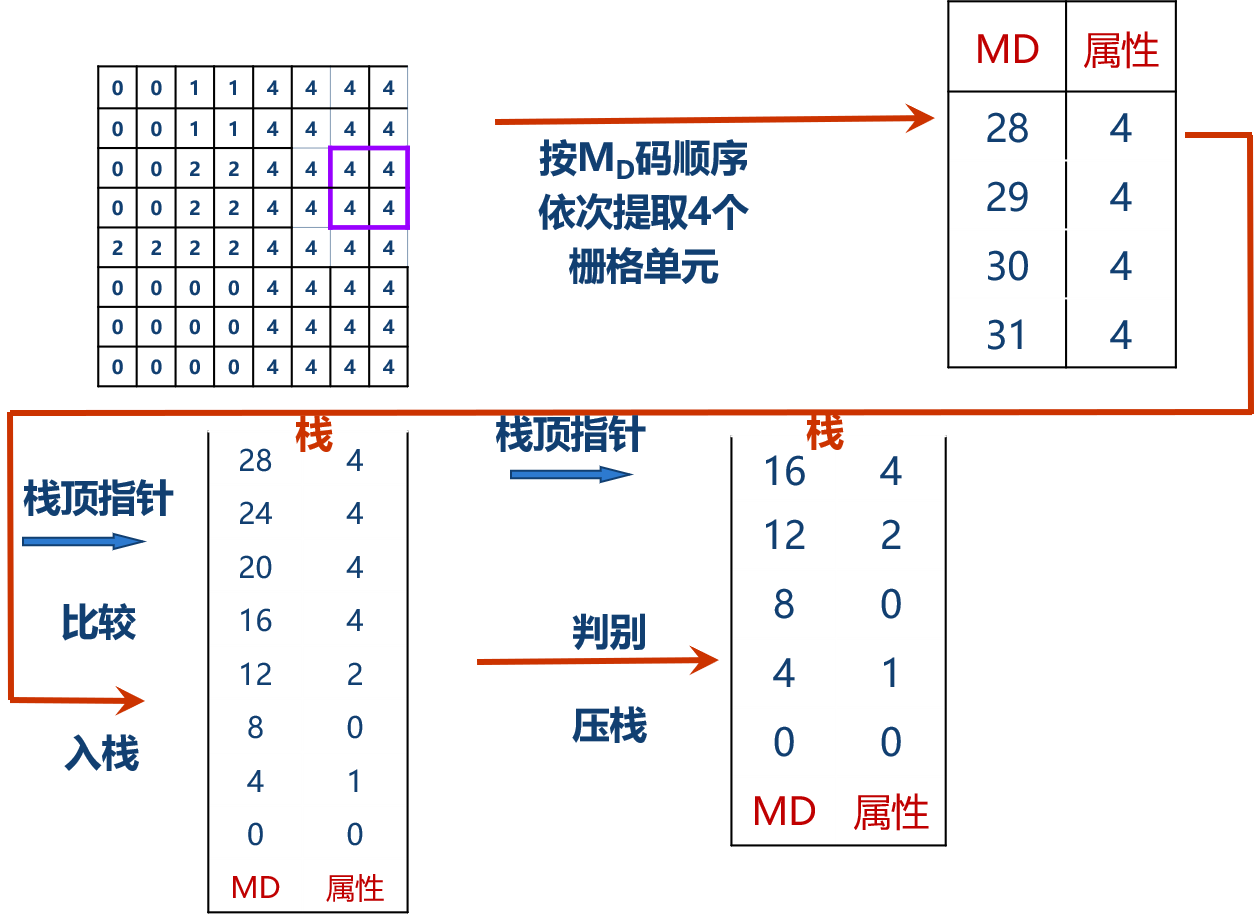
线性四叉树则只存贮最后叶结点的信息，包括叶结点的位置、深度和本结点的属性或灰度值。所谓深度是指处于四叉树的第几层上，由深度可推知子区的大小。线性四叉树叶结点的编号需要遵循一定的规则，这种编号称为地址码，它隐含了叶结点的位置和深度信息。最便于应用的地址码是十进制Morton码（MD码），十进制Morton 码是先将十进制的行列号转换成二进制数，然后将行号和列号的二进制数两两交叉, 得到以二进制数表示的复合MD码，最后，再将其转换为十进制数。用类似的方法，也可以由MD 码反求栅格单元的行列号。将编号码的栅格数据再按线性四叉树进行编码，可得到线性四叉树数据文件，其结构是MD码和属性的数据对。

如果这样的数据对仍然存在前后叶结点的值相同的情况，则可以将前后值相同的叶结点合并，形成一个新的线性表列,进一步压缩数据。这种记录方式类似游程编码，但是所合并的不是栅格单元，而是合并了代表范围大小不一的叶结点，所以称它为二维行程编码。

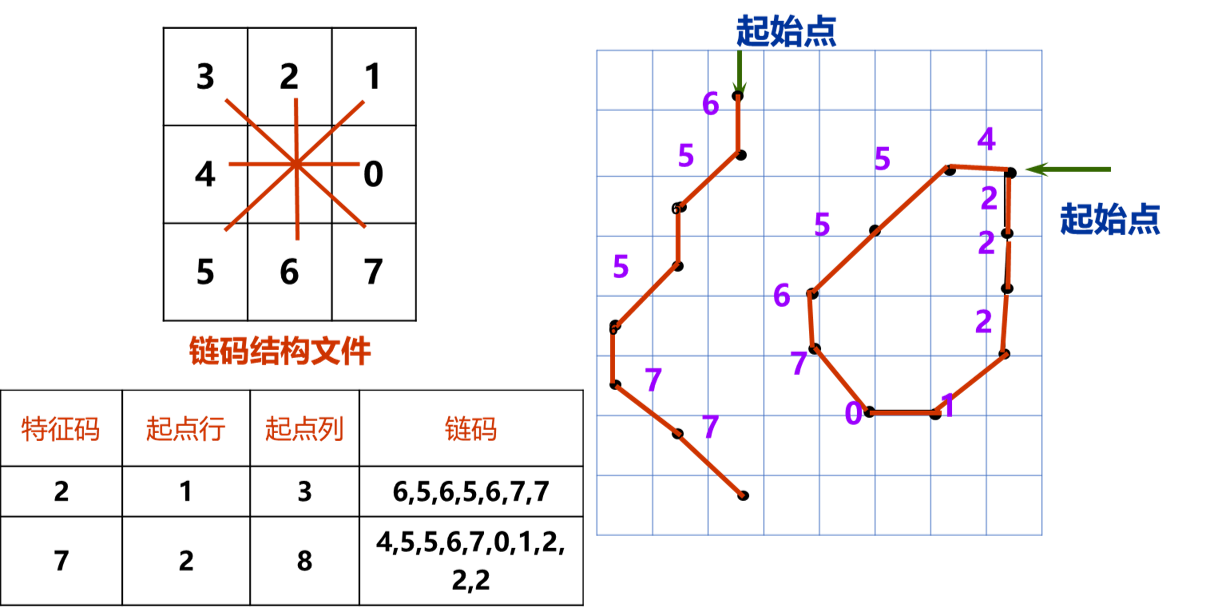
栅格数据结构还有一种叫链码数据结构。链码数据结构首先采用弗里曼码,对栅格中的线或多边形边界进行编码，然后再组织为链码结构的文件。这种结构将线状地物或区域边界表示为：由某一起始点和在某些基本方向上的单位矢量链组成。单位矢量的长度为一个栅格单元，每个后续点可能位于其前继点的8个基本方向之一。链码结构也可以有效地压缩栅格数据，同时，这种结构对计算面积、长度、转折方向和凹凸度等运算十分方便。但其缺点也很明显，就是对边界做合并和插入等编辑比较困难。同时，这种结构有些类似矢量结构，但又不具有区域的性质，因此对区域空间分析运算比较困难。

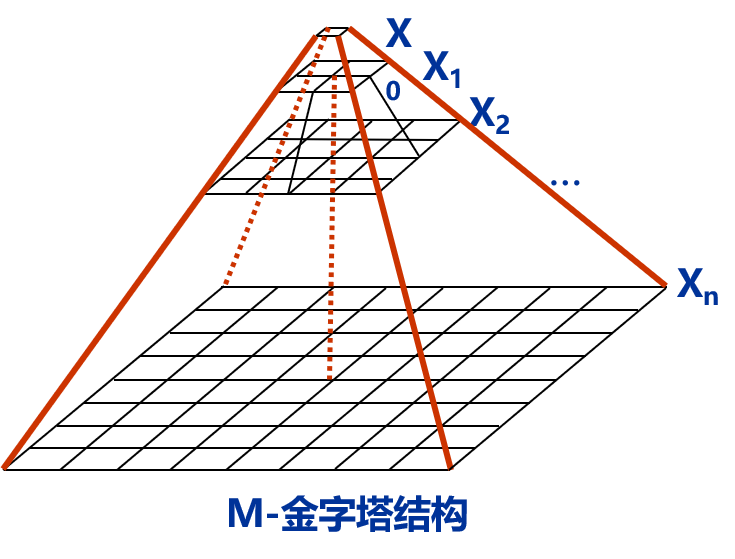
由于栅格数据数据量与分辨率直接相关，因此为满足不同的需要，就需要对栅格数据和影像数据进行多分辨率组织。解决这个问题的一种使用方法就是影像金字塔，影像金字塔是指在统一的空间参照下，根据用户需要以不同分辨率进行存储与显示，形成分辨率由粗到细、数据量由小到大的金字塔结构。

在这种金字塔结构里，图像被分层表示。在金字塔结构的最顶层，存储最低分辨率的数据；随着金字塔层数的增加，数据的分辨率依次降低；在金字塔结构的底层，则存储能满足用户需要的最高分辨率的数据。金字塔数据结构应用广泛，如对原始影像构建金字塔多分辨率结构，从而提升影像数据的显示效率。目前的电子地图中使用的地图服务也是以金字塔结构储存地图切片。