以正方形和矩形单元进行地理空间划分的规则镶嵌数据模型，采用栅格数据结构进行数据的组织；而不规则数据则采用Voronoi多边形和TIN三角网的数据结构进行数据组织。

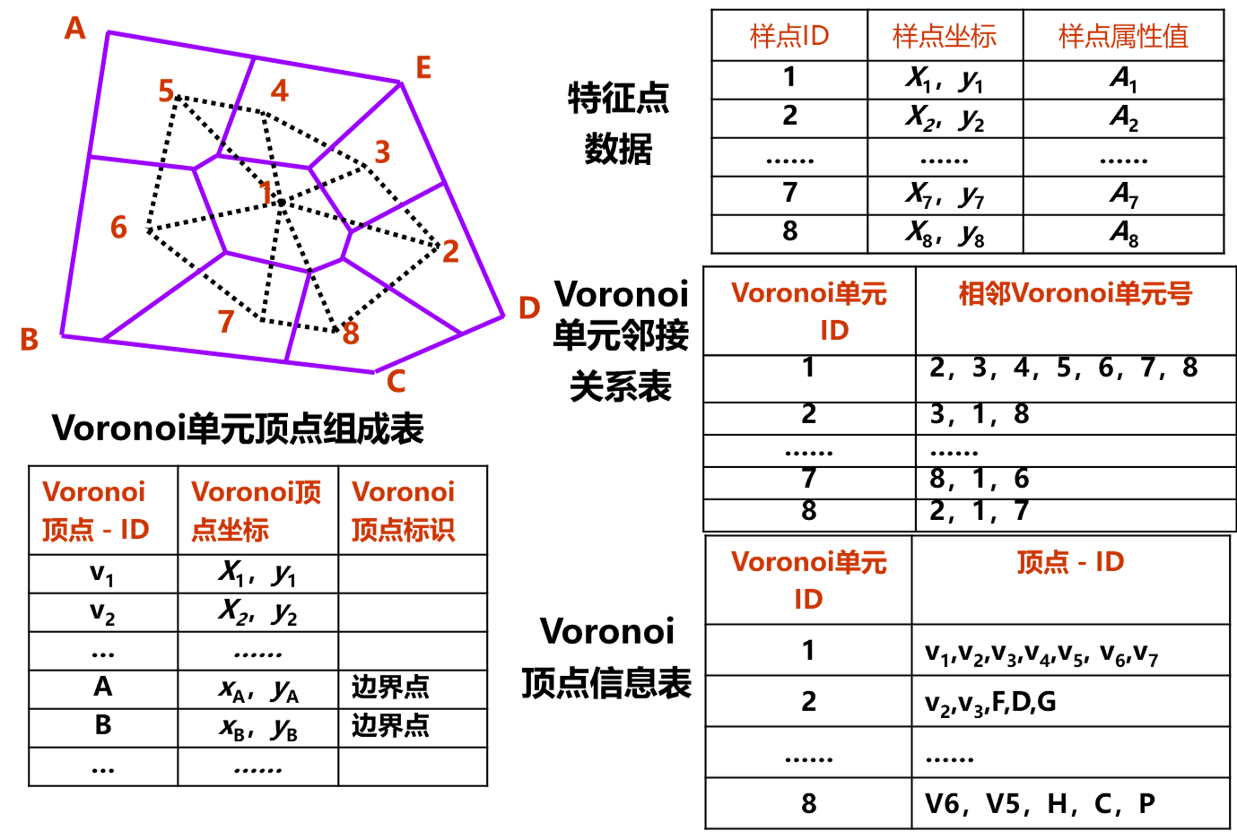
Voronoi数据结构

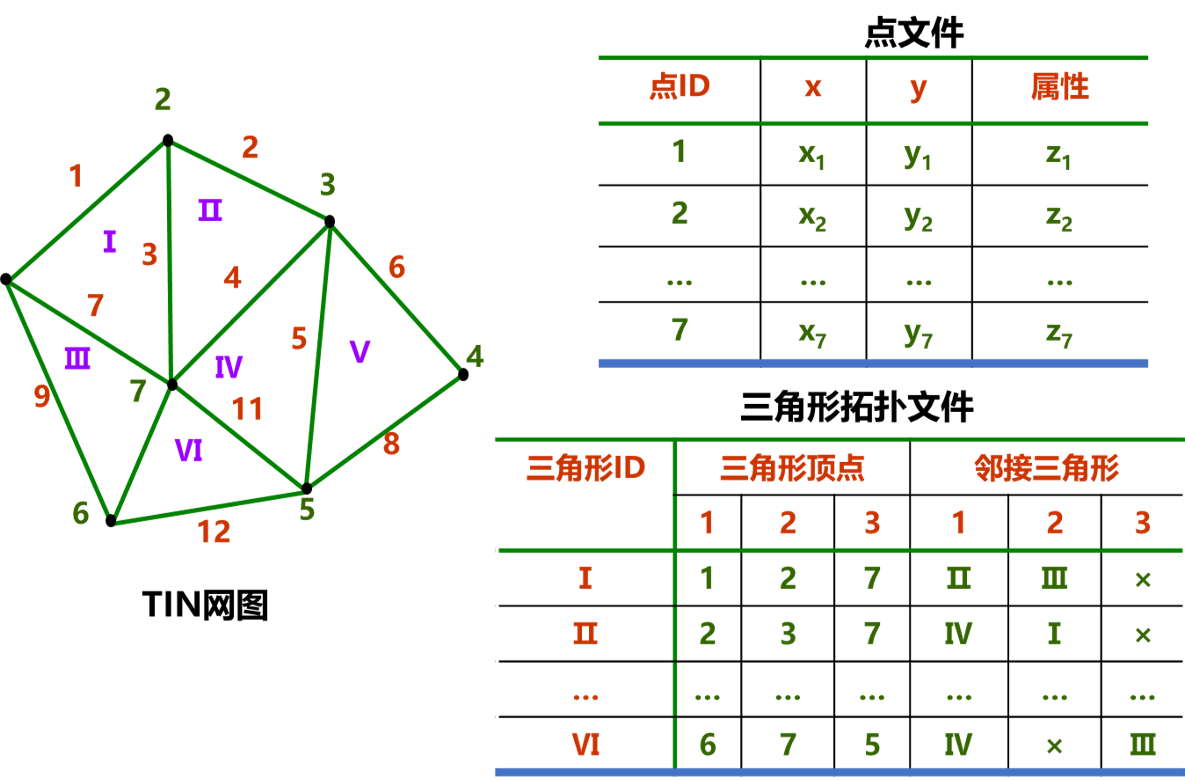
TIN数据结构

以三角形为基本对象

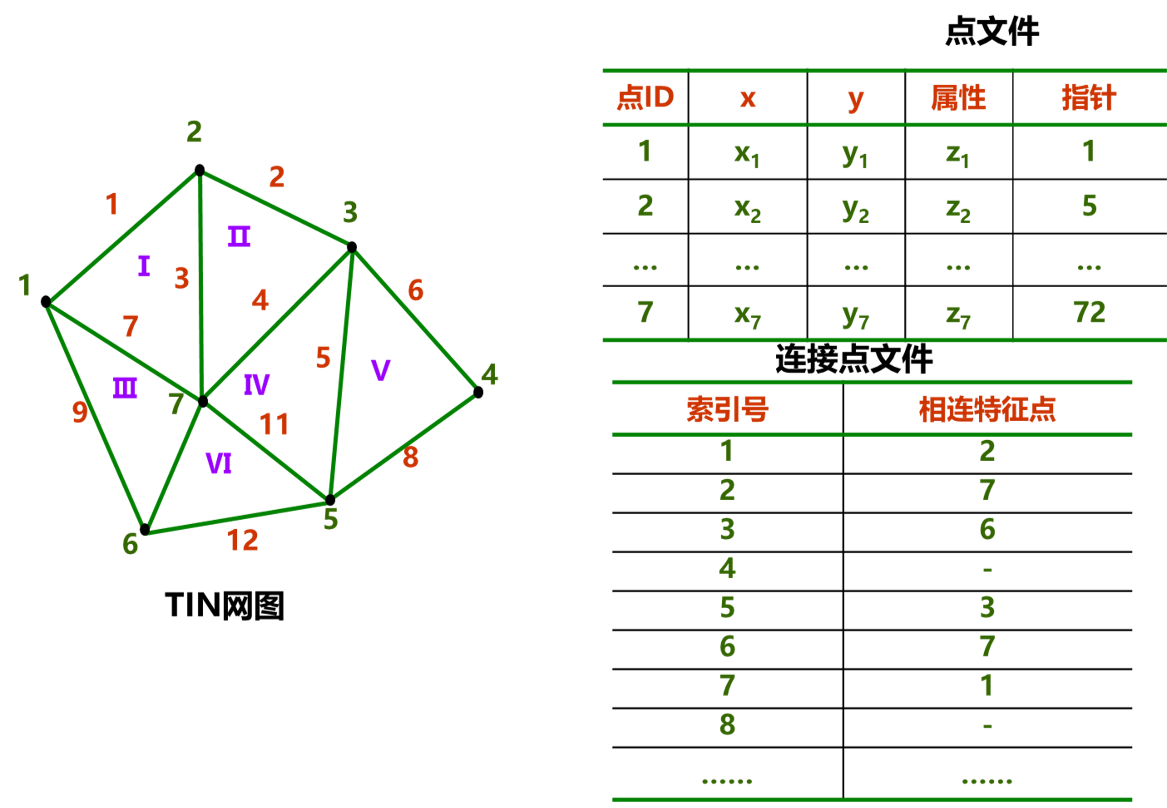
以结点为基本对象

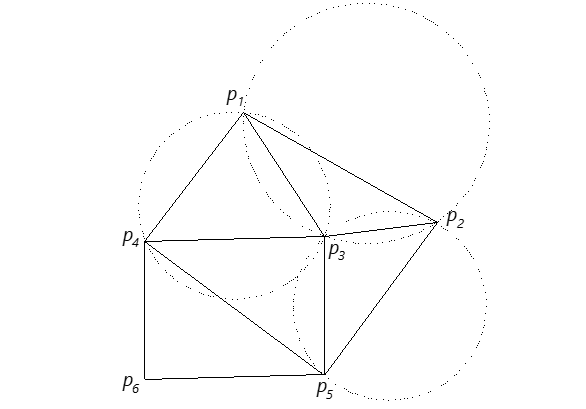
泰森多边形的建立步骤

建立泰森多边形算法的关键是对离散数据点合理地连成三角网，即构建Delaunay三角网。建立泰森多边形的步骤如下：

1、离散点自动构建三角网，即构建Delaunay三角网。对离散点和形成的三角形编号，记录每个三角形是由哪三个离散点构成的。 

2、找出与每个离散点相邻的所有三角形的编号，并记录下来。这只要在已构建的三角网中找出具有一个相同顶点的所有三角形即可。

3、对与每个离散点相邻的三角形按顺时针或逆时针方向排序，以便下一步连接生成泰森多边形。

4、计算每个三角形的外接圆圆心，并记录之。

5、根据每个离散点的相邻三角形，连接这些相邻三角形的外接圆圆心，即得到泰森多边形。对于三角网边缘的泰森多边形，可作垂直平分线与图廓相交，与图廓一起构成泰森多边形。

Delaunay三角网具有以下特征：

1、Delaunay三角网是唯一的；

2、三角网的外边界构成了点集P的凸多边形“外壳”；

3、没有任何点在三角形的外接圆内部，反之，如果一个三角网满足此条件，那么它就是Delaunay三角网。

4、如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大，从这个意义上讲，Delaunay三角网是“最接近于规则化的“的三角网。

（1）、每个Delaunay三角形的外接圆不包含面内其他任何点，即Delaunay三角网的空外接圆性质。这是创建Delaunay三角网的一项判别标准。

（2）、在由点集V中所能形成的三角网中，Delaunay三角网中三角形的最小角度是最大的。

Delaunay三角网优点：结构良好，数据结构简单，数据冗余度小，存储效率高，可适应各种分布密度的数据。