探索性数据分析(Exploratory Spatial Data Analysis, ESDA)是在不知道数据的内在关系的情况下,以空间关联测度为核心，旨在描述空间数据的空间分布特征，发现离群值，揭示空间联系的结构，给出空间异质性的形式，从而引导建模。

探索性数据分析首先分离出数据的模式和特点，再根据数据特点选择合适的模型。

探索性数据分析还可以用来揭示数据对于常见模型的意想不到的偏离。探索性方法既要灵活适应数据的结构，也要对后续分析步骤揭示的模式灵活反应。

基本分析工具

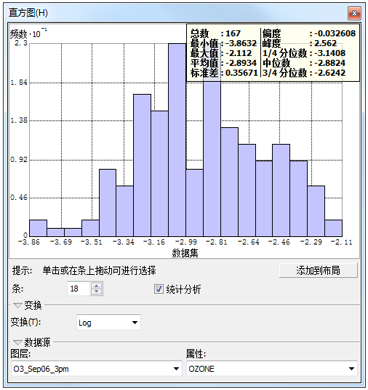
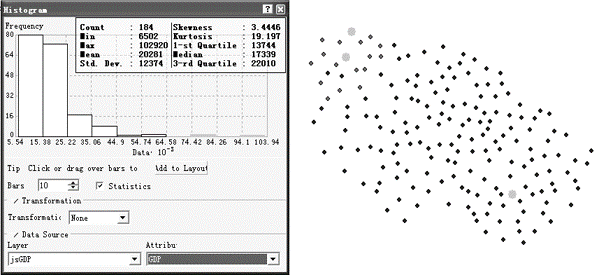
直方图:对样本数据按一定的分级方案（等间隔分级、标准差等）进行分级，统计记录落入各个级别中的个数或占总样本数的百分比，然后用条带图或柱状图表现出来。直方图可以直观反映采样数据分布特征、总体规律，可以用来检验数据分布和寻找数据离群值。

直方图中描述数据分布的重要特征包括中值、展布及对称性。快速检验正态分布的方法：平均值与中值大致相等。

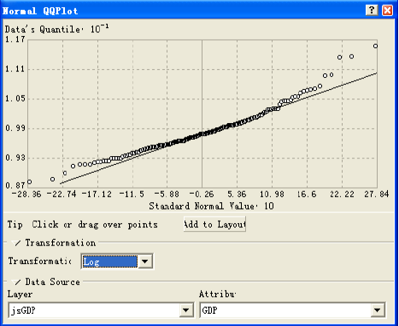
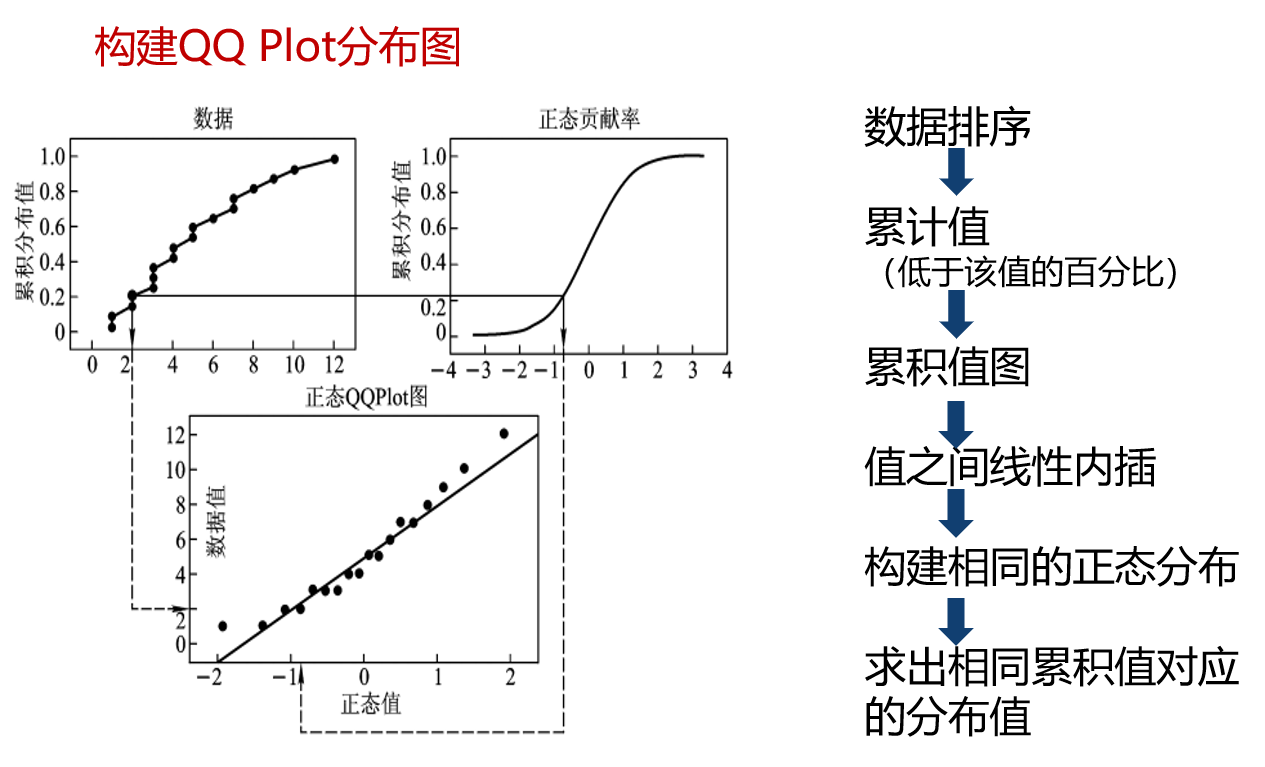
正态QQ Plot分布图：用来辅助判断样本数据是否服从正态分布。将数据的分布与标准正态分布对比，如果数据越接近一条直线，则越接近于服从正态分布。

方差变异分析工具

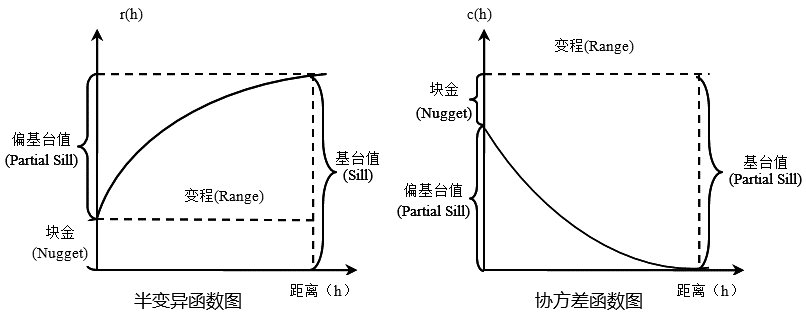
半变异函数和协方差函数把统计相关系数的大小作为一个距离的函数，是地理学相近相似定理的定量化。协方差又称半方差，表示两随机变量之间的差异。半变异值的变化随着距离的加大而增加。协方差随着距离的加大而减小。

Voronoi图：是由在样点周围形成的一系列多边形组成的。某一样点的Voronoi多边形的生成方法是：多边形内任何位置距这一样点的距离都比该多边形到其它样点的距离要近。

相邻点：和当前多边形相连的具有公共边的多边形内的点。

简化（Simple）：分配值为该多边形单元内样点的值

平均（Mean）：分配值为该单元与其相邻单元的平均值

模式（Mode）：所有的多边形单元被分成5级，分配值是此单元与相邻单元中出现频率最高的一级

聚类（Cluster）：所有的多边形单元被分成5级，若当前单元的级别与其相邻单元的级别都不同，则这个单元用灰色表示，以区别于其他单元

熵（Entropy）：所有单元都根据数据值的自然分组分配到这五级中。分配到某个多边形单元的值是根据该单元和其相邻单元计算出来的熵。

中值（Median）：分配值为该多边形单元和其相邻单元的频率分布计算的中值。

标准差（StDev）：分配值为该多边形单元和其相邻单元的计算的标准差。

四分位数间间隔（IQR）：依据该多边形单元和其相邻单元的分布计算第一和第三分位数。分配值是第三分位数和第一分位数之差。

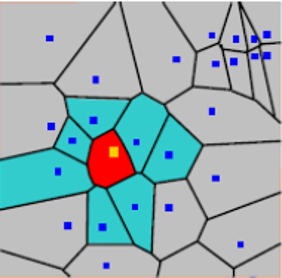
寻找数据的离群值

全局离群值指对于数据集中所有点来讲，具有很高或很低的值的观测样点。局部离群值指对于整个数据集来讲，观测样点的值处于正常范围，但与其相邻测量点比较，它又偏高或偏低。

离群点的出现有可能就是真实异常值，也可能是由于不正确的测量或记录引起的。如果离群值是真实异常值，这个点可能就是研究和理解这个现象的最重要的点。反之，如果它是由于测量或数据输入的明显错误引起的，在生成表面之前，它们就需要改正或剔除。对于预测表面，离群值可能影响半变异建模和邻域分析的取值。

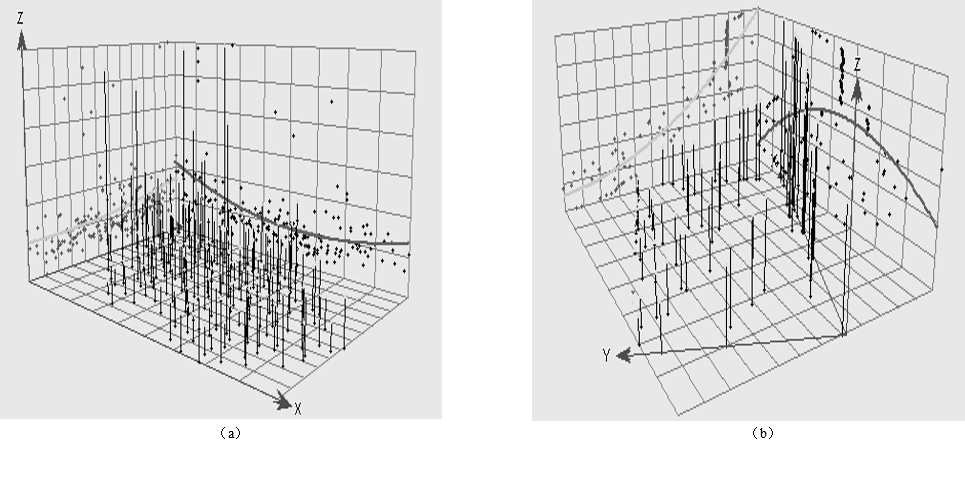
全局趋势分析

空间趋势反映了空间物体在空间区域上变化的主体特征，它主要揭示了空间物体的总体规律，而忽略局部的变异。

趋势面分析是根据空间抽样数据，拟合一个数学曲面，用该数学曲面来反映空间分布的变化情况。它可分为趋势面和偏差两大部分。

趋势面反映了空间数据总体的变化趋势，受全局性、大范围的因素影响。如果能够准确识别和量化全局趋势，在空间分析统计建模中就可以方便地剔除全局趋势，从而能更准确地模拟短程随机变异。

透视分析是探测全局趋势的常用方法，准确的判定趋势特征关键在于选择合适的透视角度。同样的采样数据，透视角度不同，反映的趋势信息也不相同。

空间自相关(spatial autocorrelation)分析包括全局空间自相关分析和局部空间自相关分析，自相关分析的结果可用来解释和寻找存在的空间聚集性或“焦点”。空间自相关分析需要的空间数据类型是点或面数据，分析的对象是具有点(面)分布特征的特定属性。

全局空间自相关用来分析在整个研究范围内指定的属性是否具有自相关性。局部空间自相关用来分析在特定的局部地点指定的属性是否具有自相关性。具有正自相关的属性，其相邻位置值与当前位置的值具有较高的相似性。

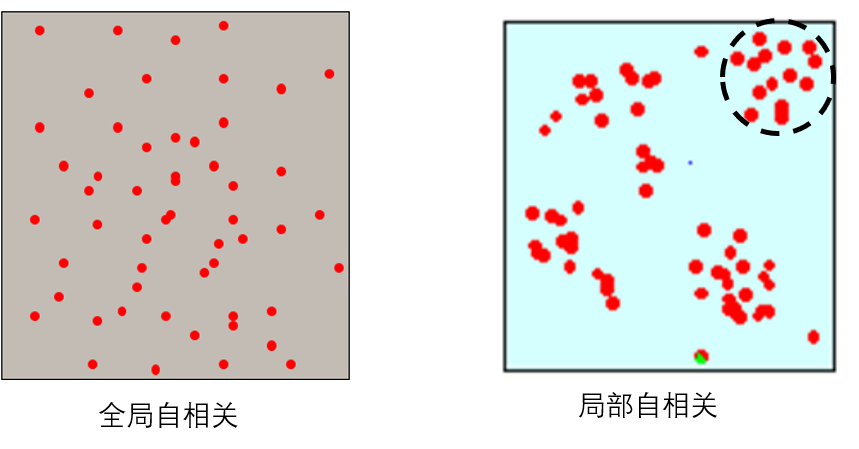
Moran’s I

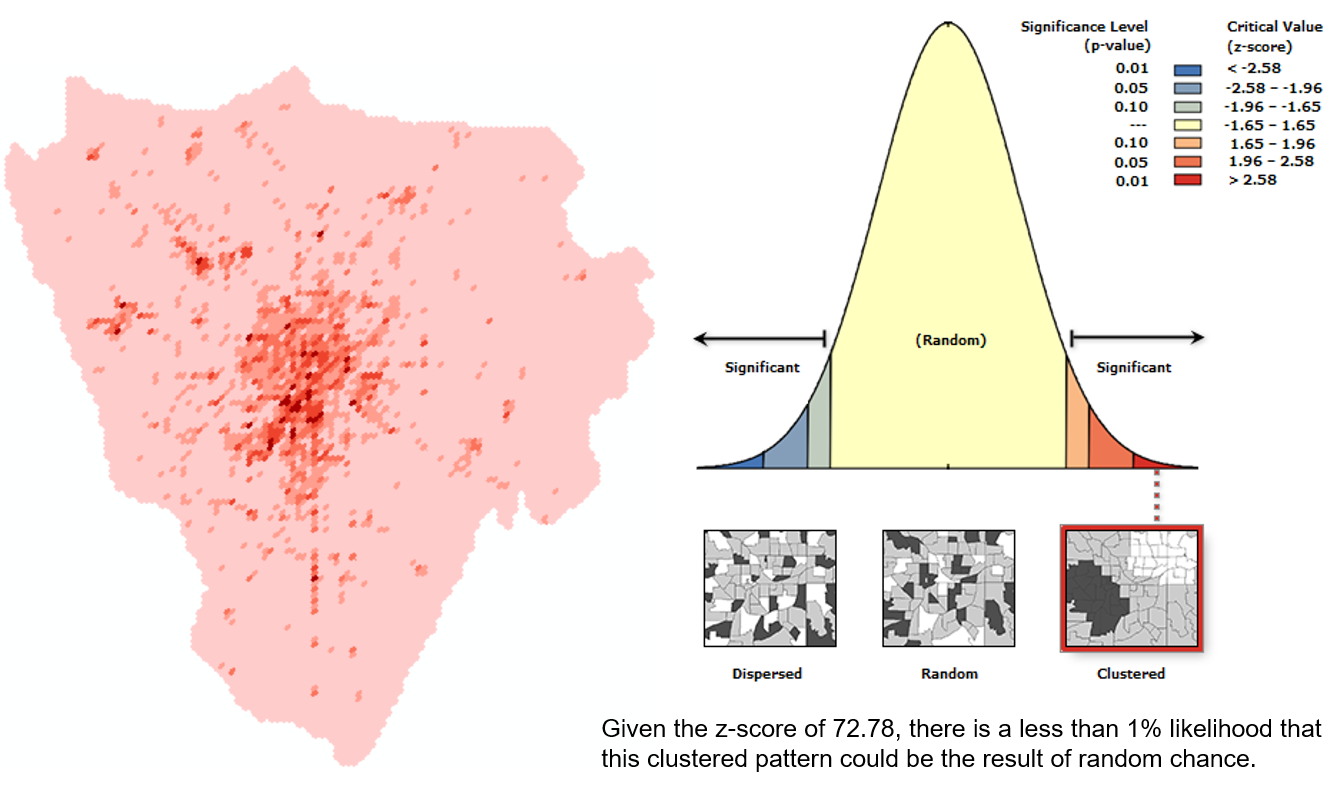
Geray C系数