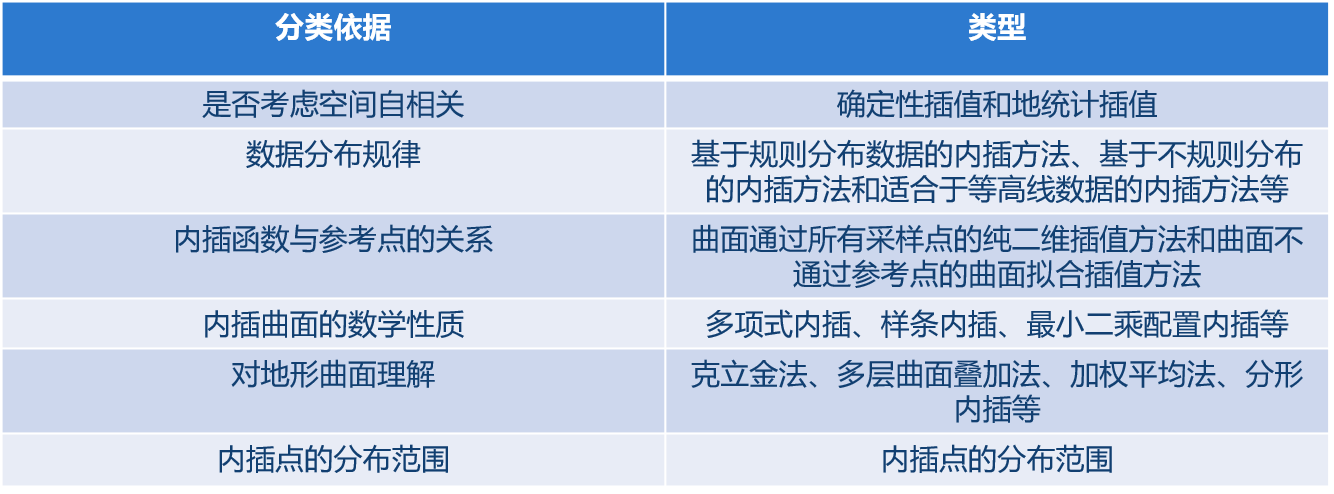
空间数据插值(spatial data interpolation)是进行数据外推的基本方法。空间内插的根本是对空间曲面特征的认识和理解，具体到方法上，即是内插点邻域范围的确定、权值确定方法（自相关程度）、内插函数的选择等3方面的问题。

整体内插：在整个区域用一个数学函数来表达地形曲面。整体内插函数通常是高次多项式，要求地形采样点的个数大于或等于多项式的系数数目。当地形采样点的个数与多项式的系数相等时，这时能得到一个唯一的解，多项式通过所有的地形采样点，属纯二维插值；而当采样点个数多于多项式系数时，没有唯一解，一般采用最小二乘法求解，即要求多项式曲面与地形采样点之间差值的平方和为最小，属曲面拟合插值或趋势面插值。

从数学角度讲，任何复杂的曲面都可用多项式在任意精度上逼近，但由于以下原因，在空间内插中整体内插并不常用：整体内插函数保凸性较差；不容易得到稳定的数值解；多项式系数物理意义不明显；解算速度慢且对计算机容量要求较高；不能提供内插区域的局部地形特征。

空间分块内插：将地形区域按一定的方法进行分块，对每一块根据地形曲面特征单独进行曲面拟合和高程内插。区域分块简化了地形的曲面形态，每一块都可用不同的曲面进行表达，一般的可按地形结构线或规则区域进行分块，而分块大小取决于地形的复杂程度、地形采样点的密度和分布；为保证相邻分块之间的平滑连接，相邻分块之间要有一定宽度的重叠，另外一种分块之间的平滑连接是对内插曲面补充一定的连续性条件。

不同的分块单元可用不同的内插函数，常用的内插数函数有：线性内插；双线性内插；多项式内插；样条函数；多层曲面叠加法等。

线性内插：如H=ax+by+c的多项式，它将分块单元内部的地形曲面视为平面。

双线性内插：在线性多项式中增加了交叉项xy，线性内插则变成双线性内插函数H=ax+by+cxy+d。

线性内插函数中有3个未知数，需要3个采样点才能惟一确定，而双线性内插函数中有4个未知数，需要4个已知点。

样条曲面可假想为将一张具有弹性的薄板压定在各个采样点上，而其他的地方自由弯曲。从数学上讲，就是一个分段的低次多项式，多项式的次数一般不超过三阶。通过样条函数，可以获取在各个采样点上具有最小曲率的拟合曲面。

与整体内插函数相比，样条函数不但保留了局部地形的细部特征，还能获取连续光滑的DEM。具有较好的保凸性和逼真性，同时也有良好的平滑性。

Coons曲面是基于任意四边形的曲面拟合方法。可用于由地形线围成的地貌形态单元。但Coons曲面仅考虑了曲边四边形的边界曲线，而没有考虑曲面内部的信息，对于恰当描述地貌形态有一定缺陷。

Geomap曲面是Bezier曲面在不规则格网划分上的推广形式。本质上，Coons和Geomap属于同一类曲面拟合问题Geomap曲面在地形上应用具有与Coons曲面类似的不足。

多层曲面叠加法认为任何一个规则或不规则的连续曲面都可看成由若干个简单的曲面来叠加逼近。在每个数据点上建立一个曲面，然后在垂直方向上将各个曲面按一定比例进行叠加，形成一张整体连续的曲面，曲面严格通过每一个数据点。多层曲面叠加法的核心是简单曲面的设计，也称为核函数。已经发展了许多种核函数的设计方法，如锥面、双曲面、三次曲面、高斯曲面（以高斯曲线为母线的旋转曲面）、Authur法、吕言法、Wild法等。

最小二乘配置是一种基于统计的内插和测量数据处理方法，它认为一个测量数据一般由 3部分构成，即趋势、信号和误差。包括最小二乘内插、最小二乘滤波和最小二乘推估。核心问题是如何建立数据之间的协方差矩阵，换句话说，就是如何解决信号的相关性规律问题。在连续表面内插中，最小二乘配置认为，数据点之间的相关规律仅与距离有关， 也就是说，距离越近，协方差越大，超过一定的距离，协方差趋于零。

克立金法（Kriging）与最小二乘配置比较类似，也是将变量的空间变化分为趋势、信号与误差3个部分，求解过程也比较相似。不同之处在于所采用的相关性计算方法上，最小二乘采用协方差矩阵，而克立金法采用半方差，或者称为半变异函数。克立金法的内蕴假设条件是区域变量的可变性和稳定性，也就说，一旦趋势确定后，变量在一定范围内的随机变化是同性变化，位置之间的差异仅仅是位置间距离的函数。通过不同数据点之间半方差的计算，可作出半方差随距离的变化的半方差图，从而用来估计未采样点和采样点之间的相关系数，进而取出内差点的高程。

有限元内插是以离散方式处理连续变化量的数学方法，其基本思路是将地形曲面分割成有限个单元的集合，单元形状可为三角形、正方形等。节点：相邻单元边界的端点（顶点、几何中心、边的中心）。自由度：每个插值条件就是一个自由度。有限元通常采用分片光滑的奇次样条函数作为单元的内插函数（也称为基函数），有限元的解是一系列基函数的线性组合。

逐点内插是以内插点为中心，确定一个邻域范围，用落在邻域范围内的采样点计算内插点的高程值。本质上是局部内插，但与局部分块内插有所不同，局部内插中的分块范围一经确定，在整个内插过程中其大小、形状和位置是不变的，凡是落在该块中的内插点，都用该块中的内插函数进行计算，而逐点内插法的邻域范围大小、形状、位置乃至采样点个数随内插点的位置而变动，一套数据只用来进行一个内插点的计算。