基于空间数据的空间统计分析与关系建模是GIS空间统计分析中除地统计分析外的另一重要组成部分。包含了一系列用于分析空间分布、模式、过程和关系的统计工具。
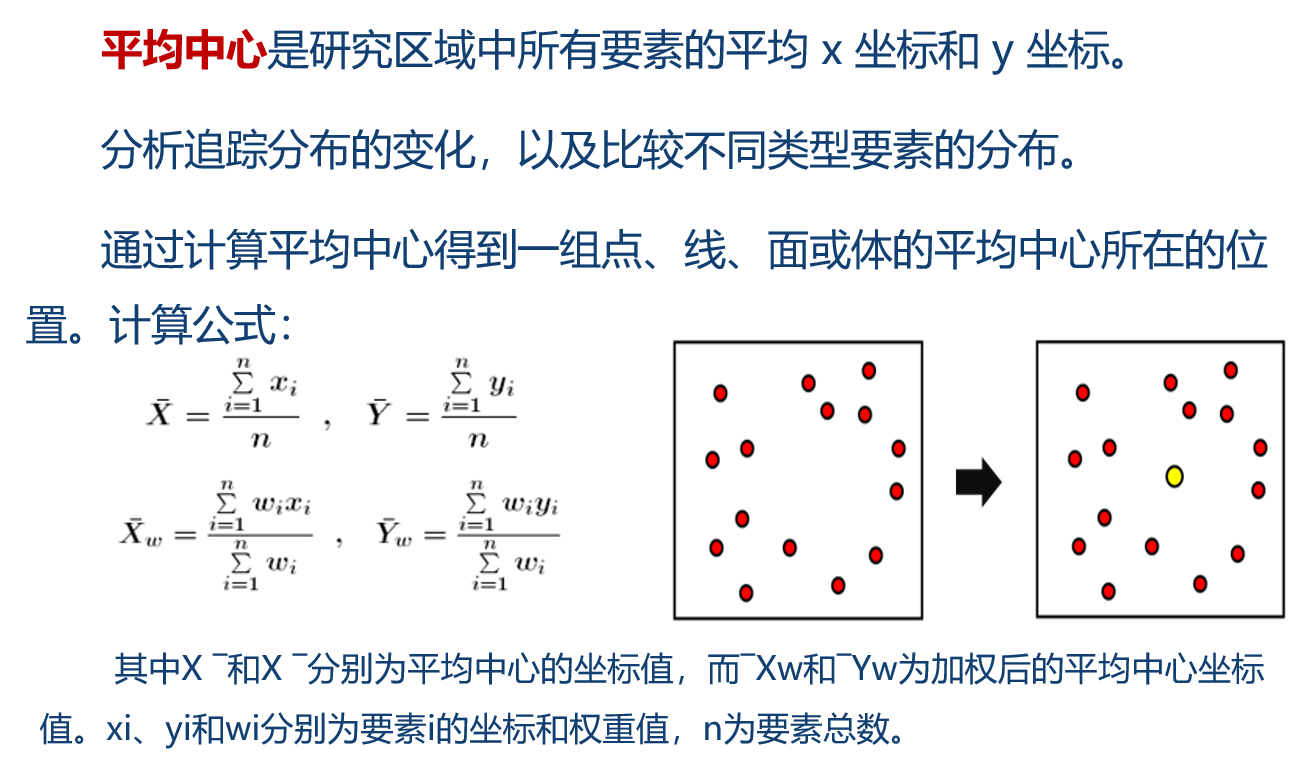
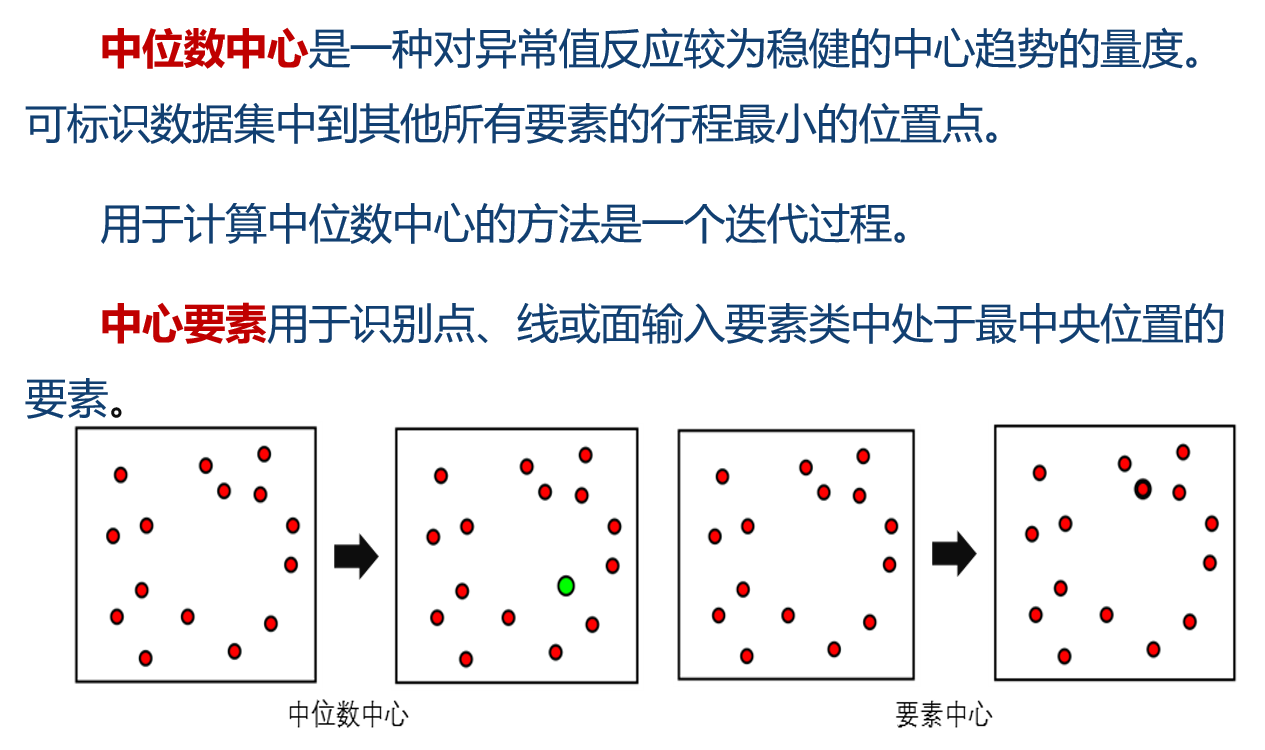
基于空间数据的空间统计,可通过度量一组要素的分布来计算各类用于表现分布特征的值,也可利用此特征值对一段时间内的分布变化进行追踪或对不同要素的分布进行比较。中级分布特征统计能够帮助了解并定量地描述要素的地理分布特征。常见的空间分布特征统计量包括一组地理要素的平均中心、中位数中心、中心要素、线性方向平均值、标准距离和方向分布等。

识别地理模式对于理解地理现象非常重要。尽管可以通过对要素制图来了解它们的总体模式及其关联值,但通过计算统计数据能够将模式量化。这样更便于比较不同分布方式或不同时段的模式。通常会先使用“分析模式”工具集中的工具进行初始分析,然后再进行更深入的分析。分布模式包括全局和局部两个层面的模式挖掘:全局模式统计;局部模式统计。
全局模式统计可提供对宏观空间模式进行量化的统计数据。解答“数据集中的要素或与数据集中要素关联的值是否发生空间聚类?”和“聚类程度是否会随时间变化?”之类的问题。局部模式统计可通过执行聚类分析来识别具有统计显著性的热点、冷点和空间异常值的位置。当根据一个或多个聚类的位置需要执行行动时,其用途特别明显。全局分析中的方法只对“是否存在空间聚类?”这样的问题回答“是”或“否”,与此不同的是,局部分析可以直观呈现聚类位置和范围。这些模型所解答的问题是“聚类(热点/冷点)的出现位置在哪里?”、“空间异常值的出现位置在哪里?”和“哪些要素十分相似?”。
全局模式分析主要包括临近度、Moran’s I莫兰指数、Geary C、G-Statistics和格林系数等统计量,每种统计量能够识别全局模式的能力各不相同。平均最邻近(Average Nearest Neighbor)只度量空间要素本身之间的邻近性,即只根据要素位置来度量空间邻近性。全局莫兰空间自相关(Global Moran's I)指数根据要素位置和要素值来度量空间自相关。G统计量高低聚类(Getis-Ord General G)可针对指定的研究区域测量高值或低值的聚集程度密度。在全局模式统计量中,可以通过空间自相关和高低值聚类对一组要素的全局模式进行分析和描述。
在局部分析统计量中,也包括用与之对应的用于局部统计分析的统计量。基于莫兰指数的聚类和异常值分析可识别具有高值或低值的要素的空间聚类.
除了分析空间模式之外,GIS空间统计分析还可用于挖掘或量化要素间关系。使用空间权重矩阵或利用回归分析可以建立空间关系模型。通常,空间关系模型通过回归模型实现。在GIS中,较为常用的空间回归模型如地理加权回归,近年来,由我国学者开发的地理探测器(GeoDetector)的使用也越来越广泛。
地理加权回归 (spatial weights matrix,GWR) 是若干空间回归技术中的一种。通过局部区域建立使回归方程拟合适合数据集中的每个要素的不同变量之间的关系。有助于对了解/预测的变量或过程提供局部模型。GWR 构建这些独立方程的方法是:将落在每个目标要素的带宽范围内的要素的因变量和解释变量进行合并。
最小二乘法(OLS) 是所有空间回归分析的正确起点。可创建一个回归方程来表示该过程。例如失业率与大专以上学历人数的关系。地理加权回归使用OLS实现。若使用得当,这些方法可提供强大且可靠的统计数据,以对线性关系进行检查和估计。
OLS属于全局空间回归模型。GWR则属于局部空间回归模型。对于空间问题,由于空间变量在局部区域的相似性和全局区域的异质性,很多情况下很难通过一个全局的OLS线性回归拟合出能够表示这些变量之间关系的线性模型,这就需要通过在不同的区域建立不同的线性回归模型对这些变量的关系进行建模,此时GWR便可以解决这类问题。
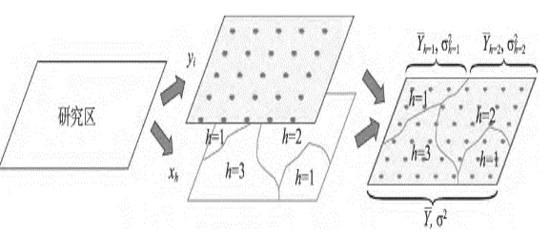
空间分层异质性简称空间分异性或区异性,是指层内方差小于层间方差的地理现象。
地理探测器(Geodetector)是探测空间分异性,以及揭示其背后驱动力的一组统计学方法。其核心思想是基于这样的假设:如果某个自变量对某个因变量有重要影响,那么自变量和因变量的空间分布应该具有相似性。既可以探测数值型数据,也可以探测定性数据,这正是地理探测器的一大优势。另一个独特优势是探测两因子交互作用于因变量。
地理探测器主要包括四个探测器,分别是分异及因子探测、交互作用探测、风险区探测和生态探测。分异及因子探测用于探测要素属性Y的空间分异性;以及探测某因子X多大程度上解释了属性Y的空间分异)。用q值度量,表达式为:
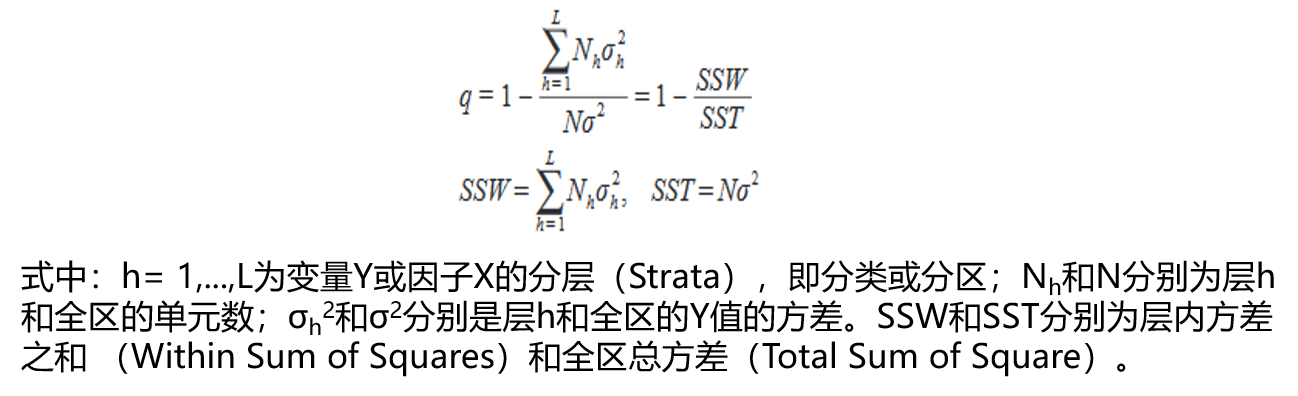
q的值域为[0, 1],值越大说明Y的空间分异性越明显;如果分层是由自变量X生成的,则q值越大表示自变量X对属性Y的解释力越强,反之则越弱。极端情况下,q值为1表明因子X完全控制了Y的空间分布,q值为0则表明因子X与Y没有任何关系,q值表示X解释了100×q%的Y。其原理如下: