2.11 Scheduling in interactive system
1. Round-Robin Scheduling (RR)
Each process is assigned a time interval, called its quantum, which it is allowed to run. It is preemptive.
Setting the quantum too short causes too many process switches and lowers the CPU efficiency, but setting it too long may cause poor response to short interactive requests. A quantum around 20-50 msec is often a reasonable compromise.
· Example: There are three batch jobs A through C, and their arrival time and running time are as follows. If use RR algorithm and the quantum is 2, what is the scheduling order? Please compute the response time of every job and the mean response time.
Job | Arrival Time | Running Time |
A | 0 | 6 |
B | 1 | 3 |
C | 3 | 2 |
Solution:
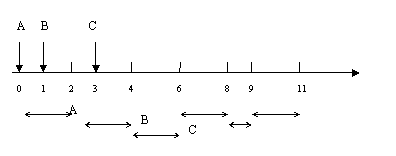
the scheduling order: A(2)→B(2)→C→A(2)→B(1)→A(2)
response time: A: 0;
B: 2-1=1;
C: 4-3=1
mean response time: (0+1+1)/3=2/3
· If the quantum is 3, repeat the example.
Solution:
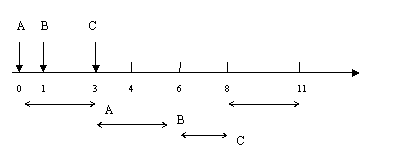
the scheduling order: A(3)→B→C→A(3)
response time: A: 0;
B: 3-1=2;
C: 6-3=3
mean response time: (0+2+3)/3=5/3
2. Priority Scheduling
Each process is assigned a priority, and the runnable process with the highest priority is allowed to run. It may be preemptive or nonpreemptive, and the priority is not changed.
· Example: There are five batch jobs A through E, and their arrival time and running time are as follows, with 1 being the highest priority. If use priority algorithm, what is the scheduling order? Please compute the turnaround time of every job and the mean turnaround time.
Job | Priority | Arrival Time | Running Time |
A | 3 | 0 | 2 |
B | 2 | 0 | 4 |
C | 1 | 3 | 1 |
D | 2 | 3 | 1 |
E | 3 | 3 | 1 |
Solution:
· nonpreemptive:
Scheduling order: B→C→D→A→E
Turnaround time: A: 8
B: 4
C: 2
D: 3
E: 6
Mean turnaround time: (8+4+2+3+6)/5=4.6
· preemptive:
Scheduling order: B(3)→C→B(1)→D→A→E
Turnaround time: A: 8
B: 5
C: 1
D: 3
E: 6
Mean turnaround time: (8+5+1+3+6)/5=4.6
· Repeat the example, with 3 being the highest priority. (omitted)
3. Multiple Queues:
The algorithm is the combination of RR and Priority algorithm, which the quantum and priority are all changed.
Processes in the highest class were run for one quantum. Processes in the next highest class were run for two quanta. Processes in the next class were run for four quanta, and so on. Whenever a process used up all the quanta allocated to it, it was moved down one class.

Question about CPU scheduling.
Compute the turnaround time of each process and the average turnaround time using:
1. Priority scheduling(non-preemptive);
2. Round-robin (quantum=6).
Please draw figures to illustrate their running procedure.
Processes | Arrival time | Run time | Priority |
A | 0 | 16 | 1 |
B | 2 | 10 | 2 |
C | 4 | 6 | 3(high) |
Answer:
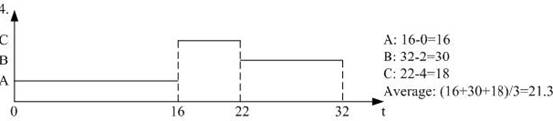
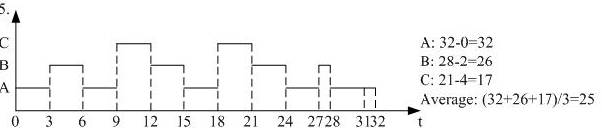
Example 1:
Round-Robin schedulers normally maintain a list of all runnable processes, with each process occurring exactly once in the list. What would happen if a process occurred twice in the list? Can you think of any reason for allowing this?
Solution:
If the process appears in the list many times, it will get more time in each cycle. This method can be used to give important processes more CPU time. But when the process is blocked, the best is to delete all items from the list of running processes.
Example 2:
Measurements of a certain system have shown that the average process runs for a time T before blocking on I/O. A process switch requires a time S, which is effectively wasted (overhead). For round-robin scheduling with quantum Q, give a formula for the CPU efficiency for each of the following:
1. Q=∞
2. Q>T
3. S<Q<T
4. Q=S
5. Q nearly 0
Solution:
1. CPU efficiency= T/(T+S)
2. CPU efficiency= T/(T+S)
3. CPU efficiency= Q/(Q+S)
4. CPU efficiency= 50%
5. CPU efficiency nearly 0
Example 3:
The CDC 6600 computers could handle up to 10 I/O processes simultaneously using an interesting form of round-robin scheduling called processor sharing. A process switch occurred after each instruction, so instruction 1 came from process 1, instruction q came from process 2, etc. the process switching was done by special hardware, and the overhead was zero. If a process needed T sec to complete in the absence of competition, how much time would it need if processor sharing was used with n processes?
Solution:
It needs nT sec







