实验背景

          用牛顿环测量透镜的曲率半径

牛顿环又称“牛顿圈”，是物理学家牛顿在1675年观察到的一种光的干涉现象，“牛顿环”是用分振幅方法实现的等厚干涉现象．它是一些明暗相间的同心圆环。在工业测量中有广泛的应用，如测量光波的波长、检测光学元件表面加工质量、测量液体、气体折射率等。

实验目的：

1、观察等厚干涉现象，加深对光波动性的理解

2、掌握用牛顿环测定透镜曲率半径的方法

3、学会调整和使用读数显微镜

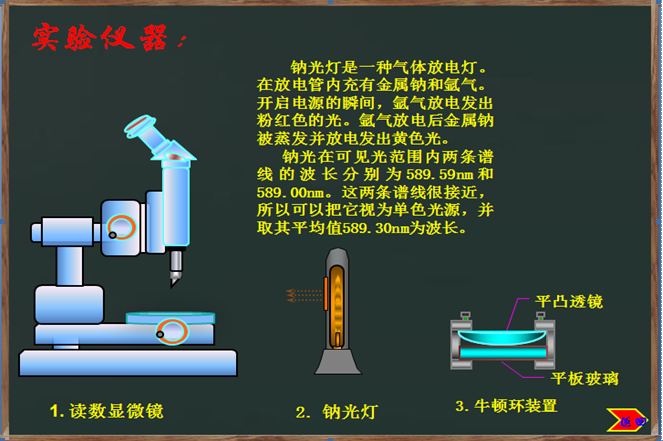
实验仪器：

牛顿环装置（其中透镜的曲率未知）、钠光灯、读数显微镜。

测量牛顿环的直径:

  读数装置：记录的位置坐标，与我们高中时所学的螺旋测微器原理是一样的，

首先我们注意一下，测微鼓轮有100小格，当转动一周时，主尺上恰好移动一个小格，主尺上的一个小格是1mm,所以测微鼓轮每一个小格代表的是0.01mm,位置坐标等于主尺上的整数部分+测微鼓轮上的小数部分（注意要估读一位）。

将一块曲率半径较大的平凸透镜的凸面放在一个光学平板玻璃上，使平凸透镜的凸面与平面玻璃相切于O点，组成牛顿环装置，则在平凸透镜凸面与平板玻璃之间形成一个以接触点O为中心向四周越来越厚的空气膜。

这是实物装置，我们需要对牛顿环装置进行调整，用眼睛在牛顿环装置上方观察，轻轻对牛顿环装置框架螺钉进行调节（切勿用力过大，以免损坏透镜）。使接触点O处于牛顿环装置中心，注意螺钉不可旋转过紧，以免接触压力过大引起透镜弹性形变，甚至损坏透镜。

实验原理：

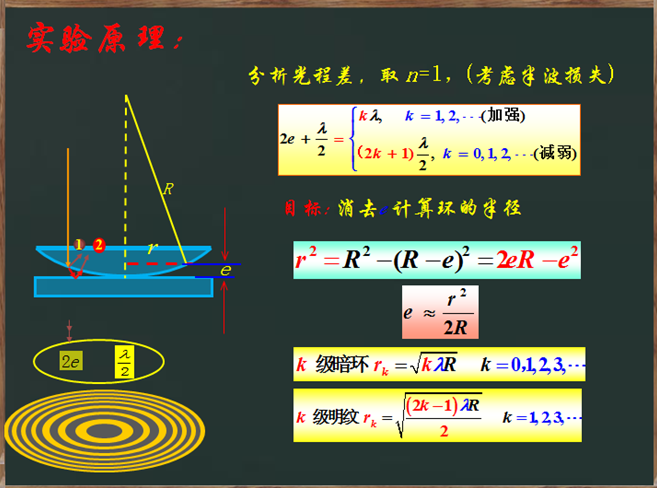
当单色平行光垂直入射时，一部分光束在AOB面上反射，一部分继续前进，到COD面上反射。这两束反射光在AOB面附近相遇，互相干涉，形成明暗相间的条纹。由于AOB面是球面，与O点等距的各点对O点是对称的，因而上述明暗条纹排成如图所示的明暗相间的圆环图样，在中心有一暗点（实际观察是一个圆斑），这些环纹称为牛顿环。

当光在空气膜的下表面反射时，由光疏介质进入光密介质，即在反射点处，则会发生相位突变，反射光的相位与入射光的相位之间相差p，与之对应的光程差为l/2，所以相干的两条光线还具有l/2的附加光程差

实验步骤：

调整读数显微镜

1.启动钠光灯电源。

2.调节目镜,看清目镜筒中的十字叉丝，当分划板上的十字刻线清晰可见时，并转动目镜，使十字叉丝的水平线与显微镜筒的移动方向平行。

3.等钠光灯电源稳定后，让读数显微镜上的45°半反镜对着钠光灯，然后调节反射片的倾斜度，得到黄色明亮的视场。

4.把牛顿环装置放到载物台中间，转动测微鼓轮：使显微镜筒平移至标尺中部，并调节调焦手轮，缓慢扭动调焦手轮，使反光镜接近牛顿环透镜组（不要相碰），缓缓转动调焦手轮，使显微镜自下而上缓慢地上升，直到看到清晰干涉条纹为止。然后再移动牛顿环装置，

5.轻轻地移动牛顿环装置的位置，使目镜中十字刻线交点与牛顿环中心大致重合。且当测微鼓轮转动移动叉丝时，叉丝与圆环相切。如叉丝倾斜可调节显微镜的目镜筒。调节后，在实验过程中不能再动牛顿环装置。

6.转动测微鼓轮,从环心（暗斑）开始，转动测微手轮。一边转动，一边数出暗纹的级数。让十字叉丝从中央缓慢向左（或向右）移至45环，然后反方向自45环向右（或向左）移动，当十字叉丝竖线与40环外侧相切时，记录读数显微镜上的位置读数，然后继续转动测微鼓轮，使竖线依次与35、30、25……5环外侧相切，并记录读数。

继续按原方向转动测微鼓轮，越过干涉圆环中心，记录十字叉丝与右边（或左边）第5--40环内切时的读数。依次填入到下面表格。

注意：测量时只往同一方向转动测微鼓轮，即我们所看到的十字叉丝只能往一个方向移动，从左侧40环到右侧40环(或者从右侧40环到左侧40环)，以消除回程差,中途不可倒转。

操作后思考题

1.如何用此实验测量光的波长？

答：在牛顿环试验中，透镜的曲率半径设为R，则对于第k 级条纹，根据光的干涉条件，它应该满足一个等式，也就是D*D=4*k*R*波长。其中D就是第k 级条纹的直径。只要用牛顿环仪器测出条纹直径，就可以通过这个公式求出波长了。

2.如何用牛顿环来检查光学平板的平整度？

答：先将样板标准面和待检验平板表面擦干净，然后使这两个面紧密接触，并尽量排除两接触面之间的空气，然后从样板上方观察会发现彩色的光圈环带。图纸上应该有要求你做到几个光圈和几道局部光圈，然后就可以知道哪个地方高了哪个地方低了。