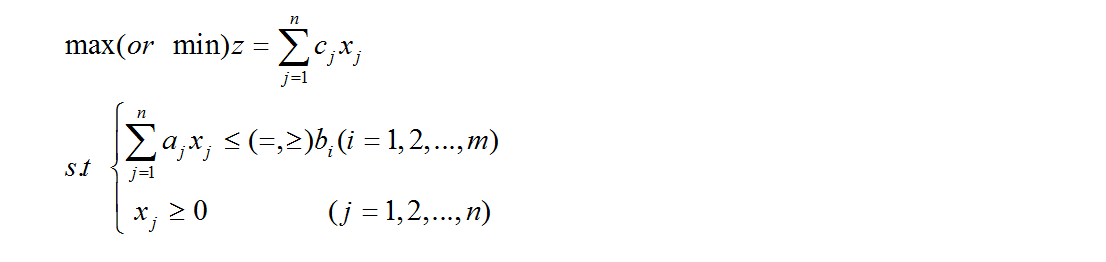决策变量

☆ 决策问题待定的量值

☆ 取值要求非负

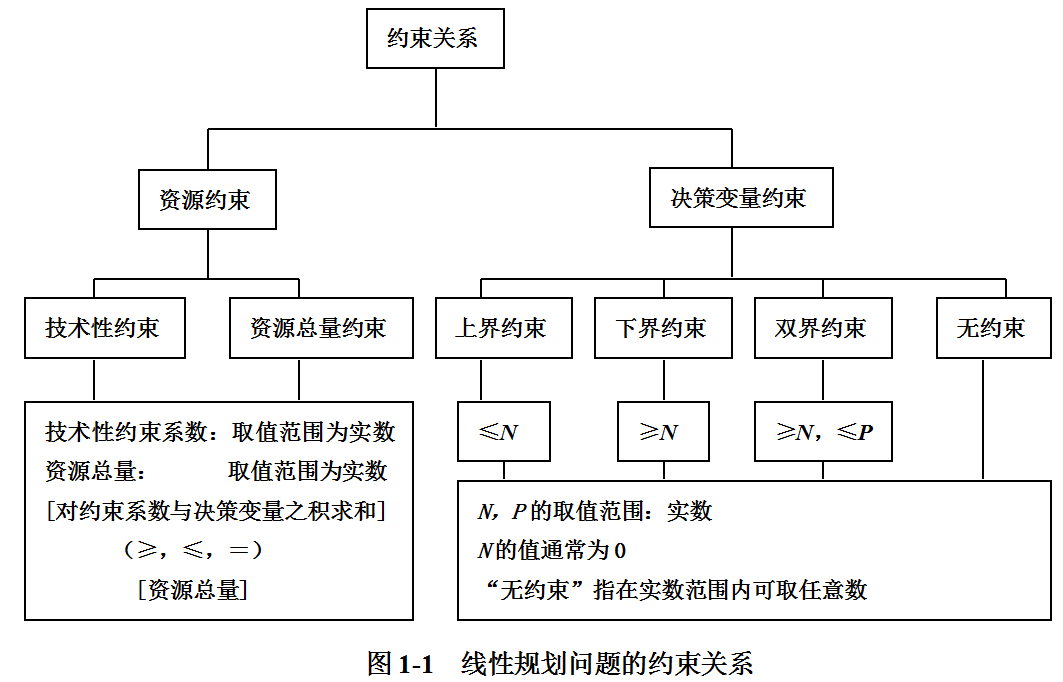
约束条件

☆ 任何管理决策问题都是限定在一定的条件下求解

☆ 把各种限制条件表示为一组等式或不等式称约束条件

☆ 约束条件是决策方案可行的保障

☆ 约束条件是决策变量的线性函数

目标函数

☆ 衡量决策优劣的准则，如时间最省、利润最大、成本最低

☆ 目标函数是决策变量的线性函数

☆ 有的目标要实现极大，有的则要求极小

用一组非负决策变量表示的一个决策方案；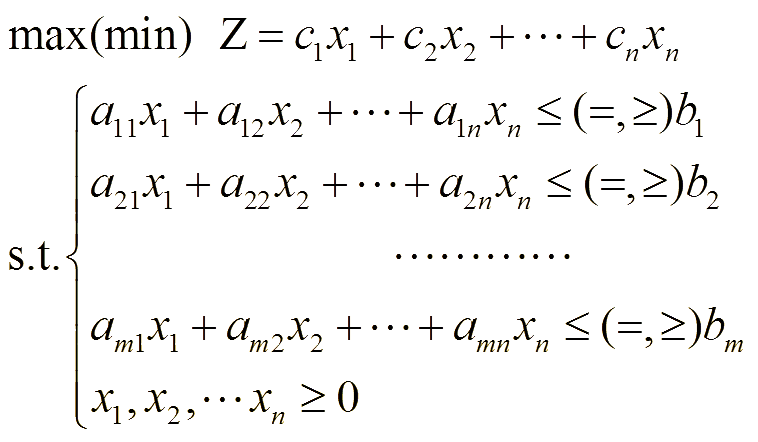

存在一组等式或不等式的线性约束条件；

有一个希望达到的目标，可表示成决策变量的线性函数。

（1）根据决策要求，确定决策变量； 

（2）根据目标要求，确定目标函数；        

（3）根据各种数量限制关系，确定约束条件。

线性规划模型的一般形式为：

线性规划模型的简写形式为：

线性规划模型的矩阵形式为：

线性规划模型的向量形式：

1、比例性假设

2、可加性假设

3、可分性假设

4、确定性假设

1、建模的基本思路和方法

2、由实际问题形成线性规划模型

3、一般线性规划问题的建模方法

4、一般线性规划模型的特点

5、建立运筹学模型的要点

线性规划模型的特征:

2.4 典型的例题分析.docx(下载附件 317.3 KB)