动态规划（Dynamic Programming）

世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。

多阶段决策

给定一个线路网络，两点之间连线上的数字表示两点间的距离(或费用) 。

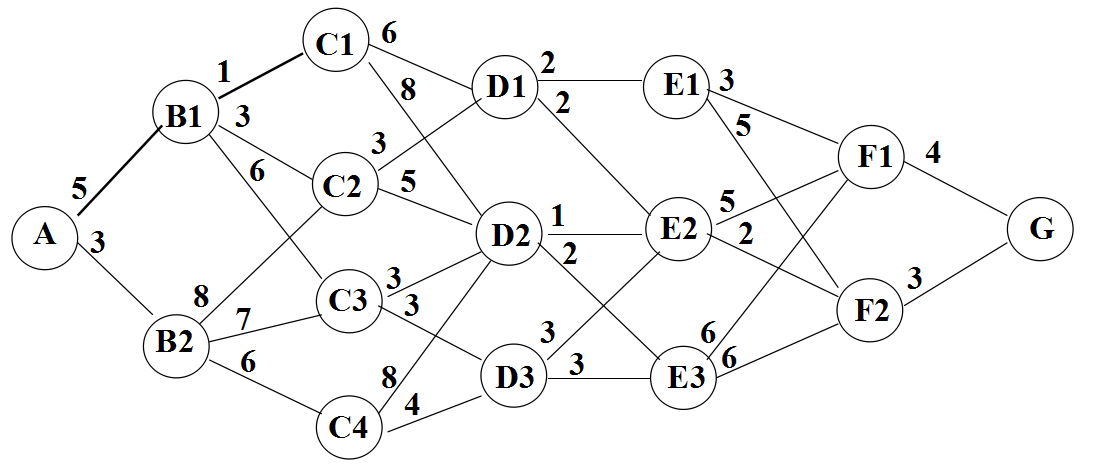
决策问题：求一条由A到G的铺管线路，使总距离为最短（或总费用最小）（最短路径问题）

（1）走一步看一步，选近的

（2）枚举法：把从A到G的每一条线路找出来，比较其长度，从而找出最短路线。

（3）隐枚举法——动态规划求解思想

① 最短路问题的特性

（4）隐枚举法——动态规划求解思想

动态规划寻找最短路线——标号法

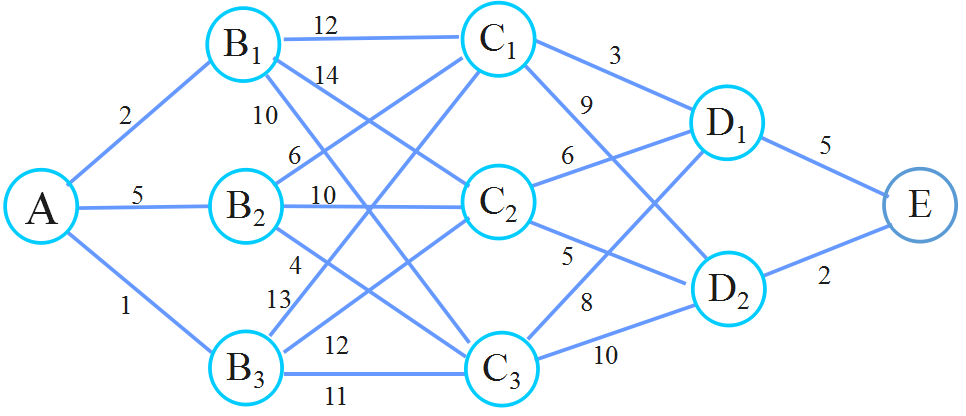
动态规划的最优化原理

动态规划方法基于R·Bellman等人提出的最优化原理：

一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。

一、动态规划的基本概念