-
1 视频
-
2 重点、难点提要
对偶理论
对偶理论是线性规划发展中最重要的成果之一,该理论认为每一个线性规划问题(称为原始问题)都有一个与它对应的对偶线性规划问题(称为对偶问题)。1928年美籍匈牙利数学家J.von.诺伊曼在研究对策论时,发现线性规划与对策论之间存在着密切的联系,并于1947年提出对偶理论。1951年G.B.丹捷格用对偶理论求解线性规划的运输问题,研究出确定检验数的位势法原理。1954年C.莱姆基提出的对偶单纯形法,成为管理决策中进行灵敏度分析的重要工具
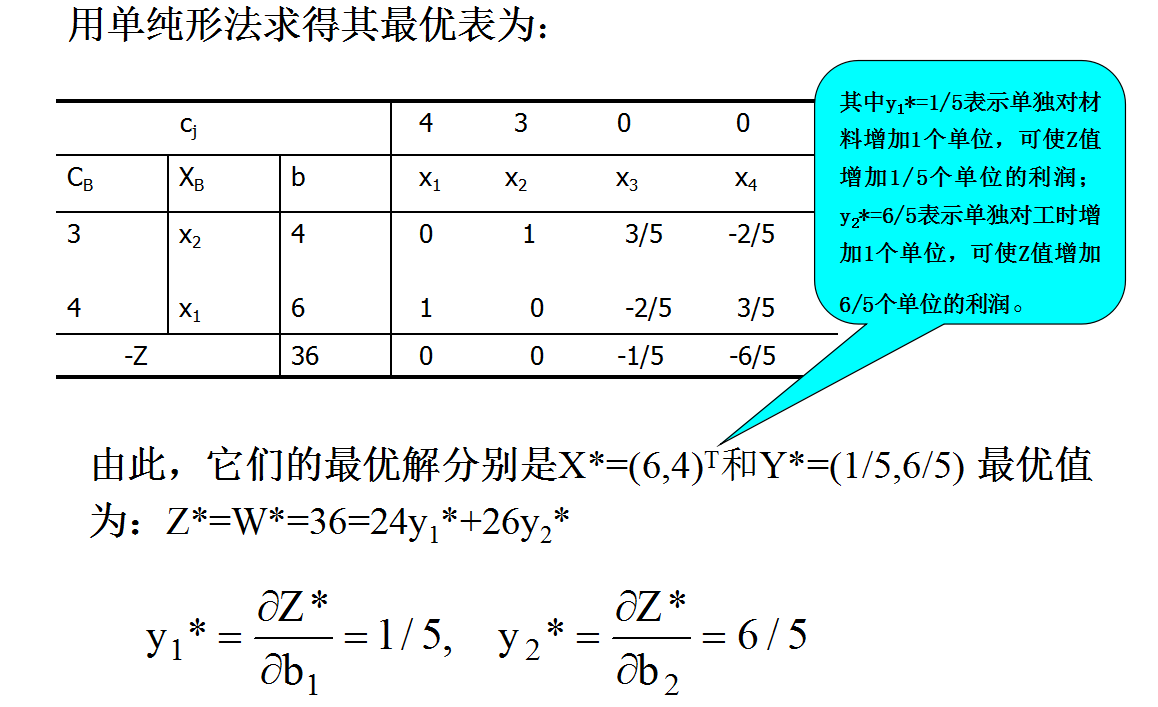
对偶理论研究线性规划的对偶关系与解的特征。根据对偶理论,在求解线性规划问题时,可同时得到其对偶问题的最优解,以及相对于各个约束条件的影子价格等信息。当对偶问题比原始问题有较少约束时,求解对偶规划比求解原始规划要方便得多。而且,对偶规划中的变量就是相应资源的影子价格。应用对偶理论,可以推出求解线性规划问题的对偶单纯形法。对偶理论在实际问题中有着广泛的应用。
对偶问题的基本定理
(1)弱对偶定理 若X(0)是原问题的可行解,Y(0)是对偶问题的可行解
(2)最优性定理 若X(0) 、 Y(0)分别是互为对偶问题LP和DP的可行解,且C X(0) = Y(0) b,则X(0)、 Y(0)分别是它们的最优解
(3)强对偶定理 若互为对偶问题之一有最优解,则另一问题必有最优解,且它们的目标函数值相等
(4)无界性原理 若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解
从上述性质中,可看到原问题与对偶问题的解必然是下列三种情况之一:
①原问题与对偶问题都有最优解,且CX=Yb;
②一个问题具有无界解,则它的对偶问题无可行解;
③两个问题均无可行解。
(5)互补松驰性定理 若X*、Y*分别是原问题和对偶问题的可行解,则X*、Y*是最优解的充要条件是:Y*XS=0,YSX*=0(其中XS,YS分别是原问题和对偶问题的松驰变量向量)。
(6)互补松驰性
X*、Y*分别是原问题和对偶问题最优解的充要条件是:
①若y*i>0,则åaijX*j=bi(资源的影子价格等于0,则该资源为紧约束)
②若åaijX*j<b,则y*i=0(资源为松约束,则其影子价格等于0)
③若X*j>0,则åaijy*i=cj(含义同前,这是把原问题作为对偶问题来看)
④若åaijy*i>cj,则X*j=0

影子价格