求解ILP问题方法的思考：

  “舍入取整”法：即先不考虑整数性约束，而去求解其相应的LP问题（称为松驰问题），然后将得到的非整数最优解用“舍入取整”的方法。这样能否得到整数最优解？否！这是因为“舍入取整”的解一般不是原问题的最优解，甚至是非可行解。

   但在处理个别实际问题时，如果允许目标函数值在某一误差范围内，有时也可采用“舍入取整”得到的整数可行解作为原问题整数最优解的近似。这样可节省求解的人力、物力和财力。

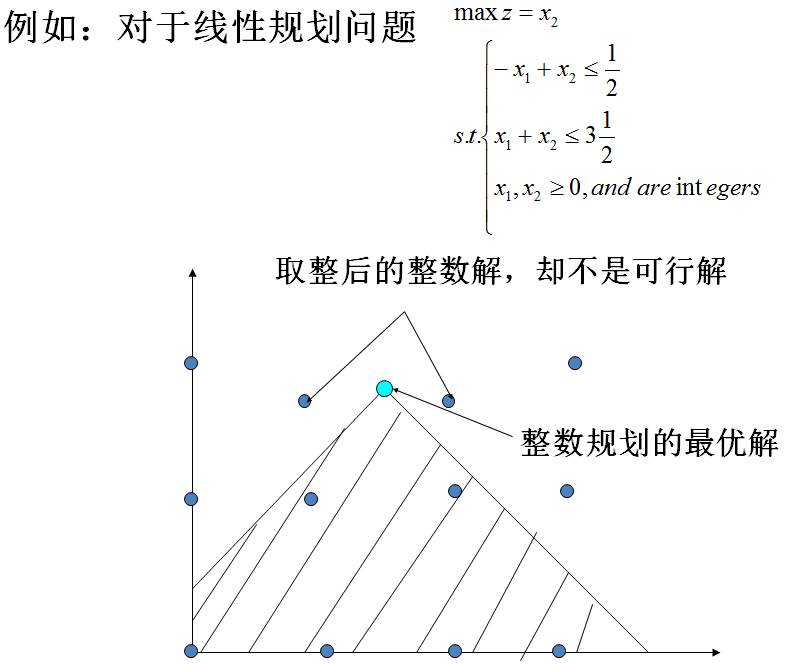
    严格地说，IP是个非线性规划问题。这是因为IP的可行解集是由一些离散的非负整数所组成，不是一个凸集。迄今为止，求解IP问题尚无统一的有效算法。但常用的有求解一般整数规划的分枝定界法、割平面法和求解0-1规划的隐枚举法。在这里我们只介绍分枝定界法和隐枚举法。

1、整数规划的分枝定界法  

分枝定界法可用于解纯整数或混合整数规划问题。在本世纪六十年代初由Land Doig和Dakin等人提出。由于该方法灵活且便于利用计算机求解，所以它是目前求解整数规划的重要方法。 

2、0-1整数规划的特殊求解

对于0-1整数规划，由于决策变量只取0，1两个值，除了能用一般整数规划的求解方法——分枝定界法求解外，还有其特殊的解法。下面介绍求解0-1规划的完全枚举法和隐枚举法。

二、整数规划模型的解法

三、0-1规划的解法