动态规划的基本概念

1.阶段(stage)

 定义：把所给问题分解成若干个相互联系的阶段，以便能按一定的顺序求解。

 变量：描述阶段的变量称为阶段变量，用k表示。

         一般根据问题的时间和空间等自然特征来划分。

2.状态

状态(state)表示每个阶段开始时过程所处的自然状况。它应该能够描述过程的特征并且具有无后向性，即当某阶段的状态给定时，这个阶段以后过程的演变与该阶段以前各阶段的状态无关，即每个状态都是过去历史的一个完整总结。通常还要求状态是直接或间接可以观测的。

状态集合：通常一个阶段有若干个状态。一般：第k阶段的状态就是第k阶段所有起始点的集合。

状态变量：描述过程状态的变量，用Sk表示第k阶段的状态集合，用sk表示第k阶段的某个状态。

状态集合

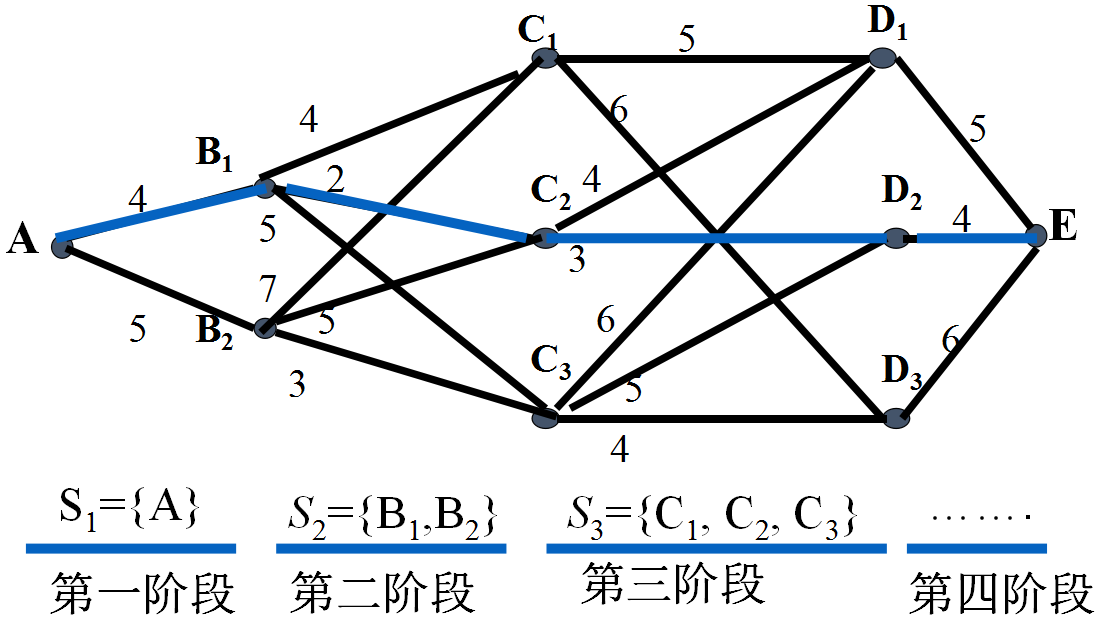
 3.决策(decision)

  定义：过程处于某状态时，可以作出的决定(或选择)。

  变量：描述决策的变量称为决策变量，用uk(sk)表示第k阶段在状态sk下的决策，显然uk是sk的函数。

  允许决策集合： sk下的决策往往有多个，它们构成的集合称为sk的允许决策集合，用Dk(sk) 表示， uk(sk) Dk(sk) 。

 4.策略

按阶段顺序排列的一组决策的集合称为策略(policy)。

由初始状态s1开始的全过程的策略记作p1,n(s1)，即p1,n(s1)={u1(s1),u2(s2),...，un(sn)}。

k子过程：从第k阶段的起始状态sk开始到终止状态sn+1结束的过程，称为问题的后部子过程或k子过程。

5.状态转移方程(state transformation equation)

描述过程演化规律的方程。

      若已知sk，当uk(sk) 确定后，则能确定sk＋1，即状态满足无后效性。

                    sk＋1＝Tr(sk , uk(sk))

6、阶段指标函数和最优指标函数

阶段指标函数：vk(sk , uk)

过程指标函数：用来衡量所实现过程优劣的数量指标，记作V k，n，对应k子过程的一个策略 p k , n(sk)产生的价值。

二、最优化原理和基本方程

三、动态规划模型的建立