一、树及其性质

连通且不含圈的无向图称为树，记为T(V,E)。

设图T=(V,E)，顶点数为n，边数为m，则以下关于树的说法是等价的。

      1.T是一棵树；

      2.T无圈，且m=n－1；

      3.T连通，且m=n－1；

      4.T无圈，但每加一新边即得唯一的一个圈；

      5.T连通，但每舍去一边就不连通；

      6.T中任意两点，有唯一链相连。

二、图的支撑树

若图G的生成子图是一棵树，则称该树为G的支撑树。

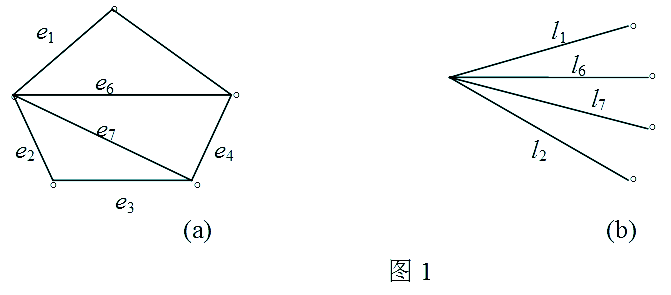
图1中(b)就是(a)的支撑树。

图G=(V,E)有支撑树的充要条件是G为连通图。

三、最小支撑树

在给定连通赋权无向图G=(V,E,W)中，求G的支撑树T=(V,Eˊ)，使E各边权Wij(≥0)的总和最小的问题称为最小支撑树问题。其数学模型为：

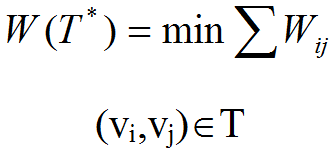
其中T*称为最小支撑树。

     许多网络问题都可归结为最小支撑树问题，如设计长度最小的公路网把若干城市联通；设计用料最省的电话线网把有关单位联系起来。

最短路问题

最短路问题是网络理论中应用最广泛的问题之一，许多优化问题可以使用这个模型，如管道铺设，设备更新，线路安排等。前面我们曾介绍了最短路问题的动态规划解法，但某些最短路的问题构造动态规划基本方程较困难，而图论方法则直观有效。

    给定D=(V,A,W)，其中wij∈W，表示弧(vi,vj)的权（可以是费用、时间、距离等）。设vs和vt是D中任意两顶点，求一条路，使它是从vs到vt的所有路中总权最小的路。其数学模型为：

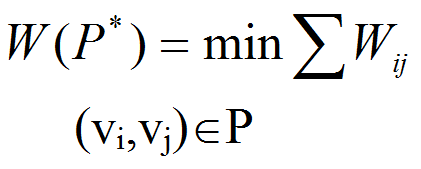
Wij≥0情况下，求最短路的Dijkstra标号法

1. 该法的基本思想是基于以下原理：若序列{vs,vi1,…vik,…vt}是从vs到vt的最短路，则序列{vs,vi1,…vik}必为从vs到vik的最短路。      

2. Dijkstra标号法的基本思想是采用两种标号：T标号与P标号，T标号为临时性标号(Temporary Label)，P标号为永久性标号(Permanent Label)。从vs开始，逐步向外探寻最短路。      

求网络中任意两点最短路的Warshall- Floyd算法

对求网络中任意两点间的最短路，当然可用改变起始点的办法，采用D氏标号法达到目的，但显然较繁。 Warshall- Floyd算法却可直接求出网络中任意两点间的最短路，且wij的正负不受限制。

二、常见的网络优化问题