一、网络与流的基本概念

1、网络流

对于有向图N=(V,A)，如果V中有一发点vs（亦称源），还有一收点（亦称为汇）记为vt，其余均为中间点，且对A中的每条弧均有权r(vi,vj)=rij0（称为弧容量），则称这样的赋权有向图N为容量网络，记为N=(V,A,R)。通过N中弧(vi,vj)的物流量xij，称为弧(vi,vj)的流量。所有弧上流量的集合X={xij}称为该网络N的一个流。

2、可行流

一般地，在容量网络D=(V,A,R)中，满足以下条件的流f，称为可行流：

    （1）弧流量限制条件    0≤xij≤rij     (vi,vj)∈A

    （2）平衡条件

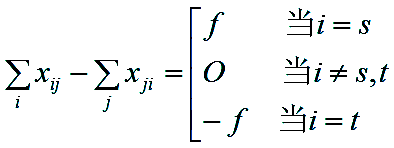
式中f为该可行流的流量，即发点的净输出量，或收点的净输入量。对于网络的流，可行流总是在存在的。如X={0}，称为零流。

3、最大流

在一网络中，流量最大的可行流称为最大流，记为X*={xij*}，其流量记为f*=f(X*)

最大流问题就是在容量网络N中，求一个可行流X={xij}，使其流量f达到最大。

4、链的前向弧与后向弧

设N=(V,A,R)中，有一可行流X={xij}，按每条弧上流量的多少，可将弧分四种类型：

        饱和弧(即xij=rij) 非饱和弧(即xij<rij)

        零流弧(即xij=0) 非零流弧(即xij>0)

5、增广链

对于可行流X, μ是一条从vs到vt的链，若+中的每弧均为非饱和弧，μ-中的每弧均为非零流弧，是称链μ是关于X的增广链。

6、割集

7、割集的截量

割集中所有弧容量之和称为该割集的截量。记为r(S,S) ，不同割集的截量不同。

8、最小割集

在一个网络中，截量最小的割集称为最小割集，记为（S*，S*），其容量（S*，S*）称为最小截量。

二、基本原理

1、流量——截量定理：网络中的任一可行流的流量恒不超过任一割集的截量。

2、最大流的充分必要条件：网络中不存在增广链。

3. 最大流最小截量定理：

    任一网络N中，最大流的流量=最小割集的截量。

三、求最大流的方法(Ford-Fulkerson标号法)

从以上概念及定理可知，要判断可行流f是否最大流有两种途径：

  1）能否找出可行流f的增广链，若能，则f不是最大流，否则f是最大流。

  2）V(f)是否等于最小截量，若等，则f是最大流，否则f不是最大流。

标号法的基本思想：从可行流f出发，由Vs开始，用对D中的每个顶点进行标号的办法找f的增广链。若无，则f为所求的最大流。否则，在增广链上进行调整。