1、教学模型

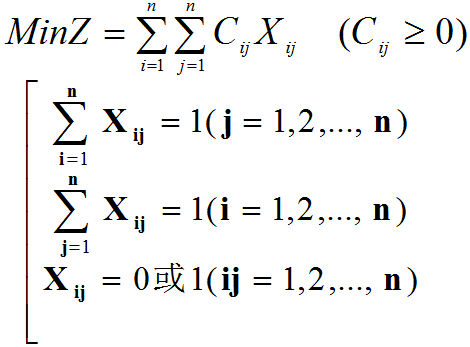
2、特点

1、匈牙利法的基本思想

匈牙利法主要基于指派问题的第（3）个特点。即从效率矩阵的每行或每列减去一个常数，指派问题的最优解不变。由此，我们可以让每行或每列减去一个数后，出现0元素，然后，再给费用为0元素的相应变量指派为1，以使变换后的目标函数为0，从而达到最优。

2、匈牙利法的计算步骤

第一步：变换指派问题的系数矩阵，使在各行各列中都出现0元素。

(1)从系数矩阵的每行元素中减去该行的最小元素；

(2)再从所得系数矩阵的每列元素中减去该列的最小元素，若某行（列）已有0元素，则不需再减了；

第二步：进行试指派，以寻求最优解。按以下步骤进行。

经第一步变换后，系数矩阵中每行每列中都已有0元素，但需要找出n个独立的0元素。如能找出，就以这些独立的0元素对应解矩阵（xij）中的元素为1，其余为0，这就得到最优解。

具体步骤为：

①从只有一个0元素的行（列）开始，给这个0元素加圈，记作◎。然后划去◎所在列（行）的其它0元素，记作ø

②给只有一个0元素列（行）的0元素加圈，记作◎；然后划去◎所在行的0元素，记作ø。

③反复进行①、②步骤，直到所有0元素都被圈出和划掉为止。

④若仍有没有划圈的0元素，且同行（列）的0元素至少有两个（表示对这人可以从两项任务中指派其一），则从剩有0元素最少的行（列）开始，比较这行各0元素所在列中0元素的数目，选择0元素少的那列的这个0元素加圈（表示选择性多的应该先满足选择性少的），然后划掉同行同列的其它0元素。可反复进行，直到所有0元素都已划圈或划掉为止。

⑤若◎元素的数目m等于矩阵的阶数n，那么这指派问题的最优解已得到；若m<n，则转入下一步。 

第三步：作最少的直线覆盖所有0元素，以确定该系数矩阵中能找到最多的独立0元素。为此按以下步骤进行：

①对没有◎的行打√；

②对已打√的行中所有含0元素的列打√；

③再对打有√的列中含有◎元素的行打√；

④重复②、③直到得不出新的打√的行、列为止；

⑤对没有打√的行画一横线，有打√的列画一纵线，这就得到覆盖所有0元素的最少直线数。

3、关于求最大化的指派问题

4、非平衡的指派问题

四、指派问题

7.4 主要解题方法和典型例题分析.docx(下载附件 139.37 KB)