变量的多重分配赋值
可以在同一行上拥有多个赋值。 例如,
a = 2; b = 7; c = a * b
MATLAB执行上述语句并返回以下结果
c = 14

目录
Matlab基本数据类型


变量的赋值:
MATLAB不需要任何类型声明或维度语句。当MATLAB遇到新的变量名称时,它将创建变量并分配适当的内存空间。在MATLAB环境中,每个变量都是数组或矩阵。
如果变量已经存在,则MATLAB将使用新内容替换原始内容,并在必要时分配新的存储空间。
例如,
total = 136;
上述语句创建一个名为total的1x1矩阵,并将值136存储在其中。
可以在同一行上拥有多个赋值。 例如,
a = 2; b = 7; c = a * b
MATLAB执行上述语句并返回以下结果
c = 14
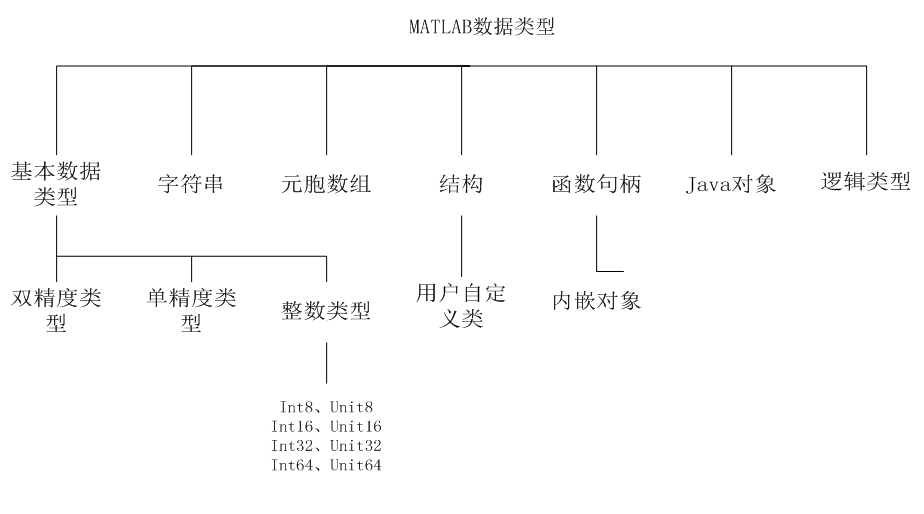
下表显示了MATLAB中最常用的数据类型 :
| 数据类型 | 描述 |
| int8 | 8位有符号整数 |
| uint8 | 8位无符号整数 |
| int16 | 16位有符号整数 |
| uint16 | 16位无符号整数 |
| int32 | 32位有符号整数 |
| uint32 | 32位无符号整数 |
| int64 | 64位有符号整数 |
| uint64 | 64位无符号整数 |
| single | 单精度数值数据 |
| double | 双精度数值数据(也是matlab的默认数值类数据类型) |
| logical | 逻辑值为1或0,分别代表true和false |
| char | 字符数据(字符串作为字符向量存储) |
| 单元格阵列 | 索引单元阵列,每个都能够存储不同维数和数据类型的数组 |
| 结构体 | C型结构,每个结构具有能够存储不同维数和数据类型的数组的命名字段 |
| 函数处理 | 指向一个函数的指针 |
| 用户类 | 用户定义的类构造的对象 |
| Java类 | 从Java类构造的对象 |

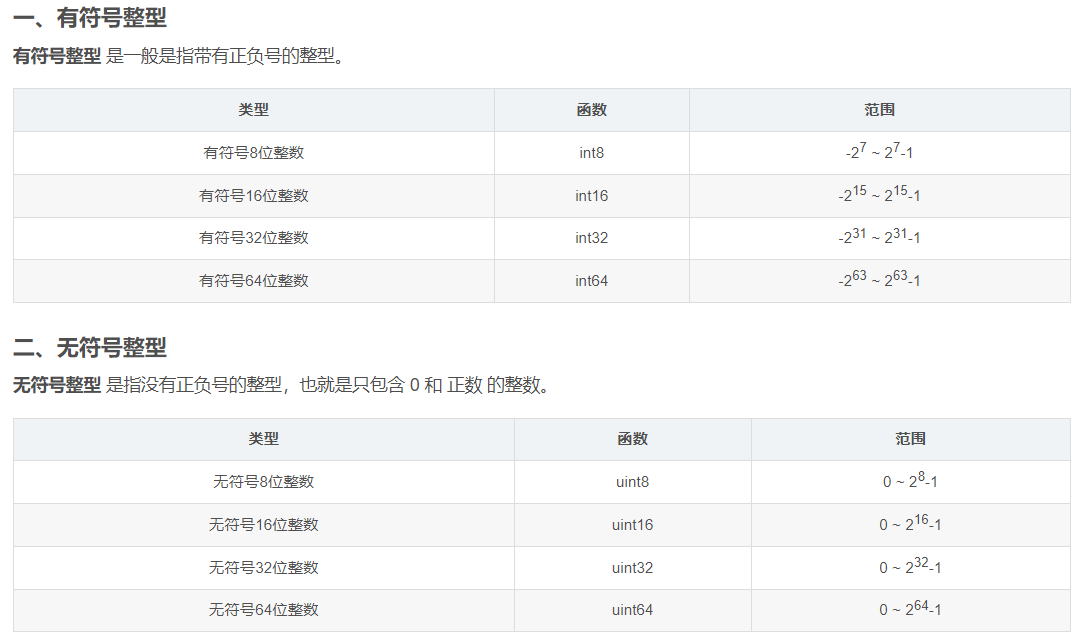
三、整型创建
由于 Matlab 中数值的默认存储类型是 双精度浮点型,因此必须通过上表中的函数将其转换成指定类型的整型。
如果不理解,可以把x=数据类型(数值)当作对其赋值给了相应数据类型的值。举个例子,x=32 和 x=double(32)是相同的,就当 matlab 默认将x变成了 double 类型的值。
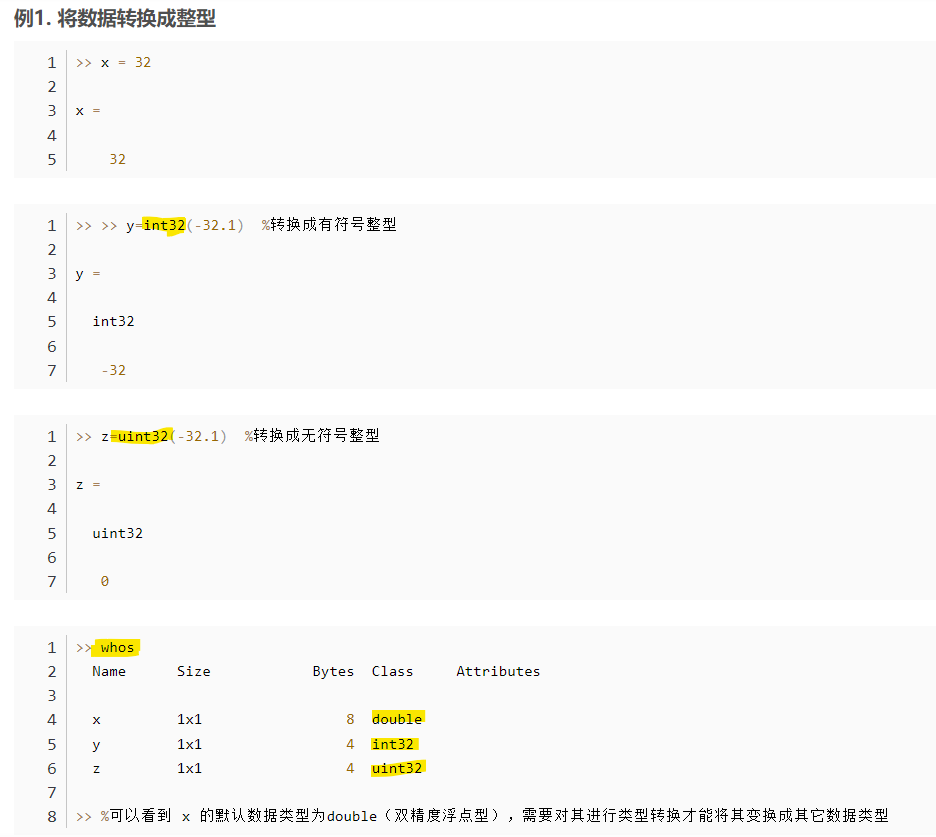
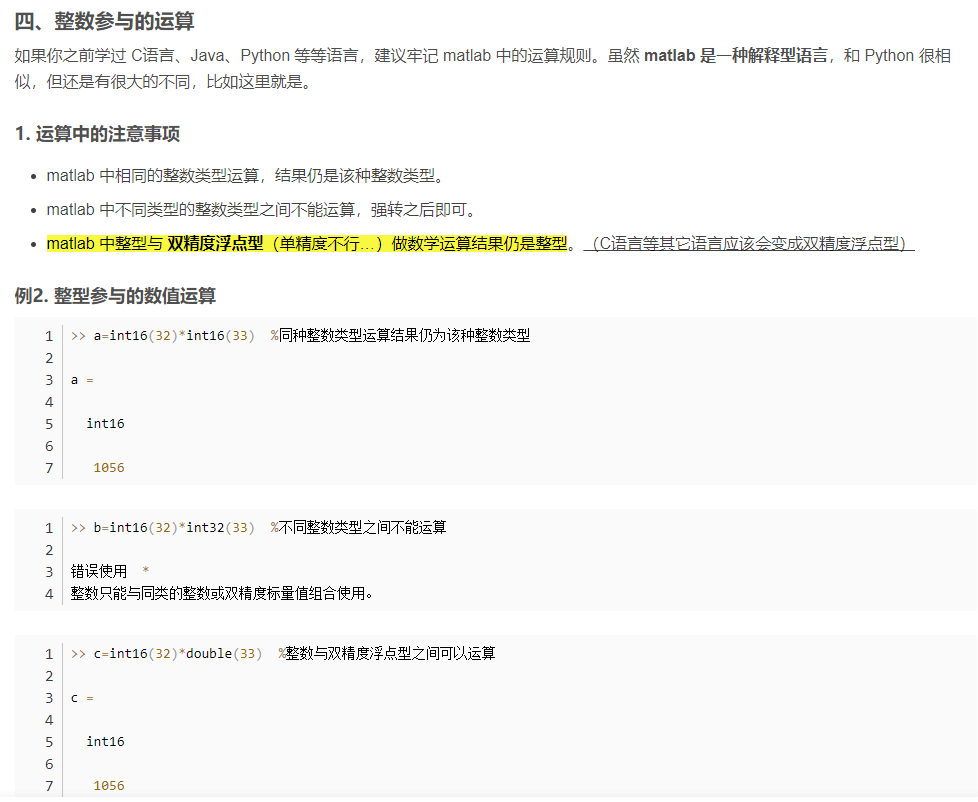
使用以下代码创建脚本文件(datatype1.m)
str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)
当上述代码被编译和执行时,它产生以下结果 -
str =
'Hello World!'
n =
2345
d =
2345
un =
uint32
790
rn =
5.6789e+03
c =
int32
5679
复数由两个单独的部分组成:实部和虚部。基本虚数单位等于 -1的平方根。这在 MATLAB中通过以下两个字母之一表示:i或 j。以下语句显示了一种在 MATLAB 中创建复数值的方法。变量 x被赋予了一个复数值,该复数的实部为 2,虚部为 3
x = 2 + 3i;
创建复数的另一种方法是使用 complex函数。此函数将两个数值输入组合成一个复数输出,并使第一个输入成为实部,使第二个输入成为虚部:
x = rand(3) * 5;
y = rand(3) *(-8);
z = complex(x, y)
z =
4.7842 -1.0921i 0.8648 -1.5931i 1.2616 -2.2753i
2.6130 -0.0941i 4.8987 -2.3898i 4.3787 -3.7538i
4.4007 -7.1512i 1.3572 -5.2915i 3.6865 -0.5182i
您可以使用 real和 imag函数分解复数,捕获其实部和虚部:
zr = real(z)
zr =
4.7842 0.8648 1.2616
2.6130 4.8987 4.3787
4.4007 1.3572 3.6865
zi = imag(z)
zi =
-1.0921 -1.5931 -2.2753
-0.0941 -2.3898 -3.7538
-7.1512 -5.2915 -0.5182
可以使用abs函数来得到复数的绝对值(辐值)
z=3+4i;
z_v=abs(z)
| 函数 | 作用 |
| abs | 绝对值和复数幅值 |
| angle | 相位角 |
| complex | 创建复数数组 |
| conj | 复共轭 |
| cplxpair | 将复数排序为复共轭对组 |
| i , j | 虚数单位 |
| imag | 复数的虚部 |
| isreal | 确定数组是否为实数数组 |
| real | 复数的实部 |
| sign | Sign 函数(符号函数) |
| unwrap | 更正相位角以生成更平滑的相位图 |
默认情况下,MATLAB显示四位小数位数。这称为:短格式。
但是,如果要更精确,则需要使用format命令。
format short | 5位定点表示(默认) |
format long | 15位定点表示 |
format short e | 5位浮点表示(科学计数法) |
format long e | 15位浮点表示(科学计数法) |
format short g | 5位定点和5位浮点中自动选择最好格式表示 |
format long g | 15位定点和15位浮点中自动选择最好格式表示 |
format hex | 16进制格式表示 |
format + | 在矩阵中,用符号+、-和空格表示正号、负号和零 |
format long 命令将数字舍入到小数点后15位
>> format long
x = 7 + 10/3 + 5 ^ 1.2
x =
17.231981640639408
另一个示例如下 :
>> format short
x = 7 + 10/3 + 5 ^ 1.2
x =
17.2320
format bank 命令将数字舍入到小数点后两位。
>> format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6
weekly_wage = 1064.70
format short e命令以指数形式显示四位小数加上指数。
>> format short e
4.678 * 4.9
ans =
2.2922e+01
format long e命令允许以指数形式显示十六位小数加上指数。
>> format long e
x = pi
x =
3.141592653589793e+00format rat命令给出计算结果最接近的合理表达式。
>> format rat
4.678 * 4.9
ans =
2063/90| 运算符 | 使用说明 |
| + | 相加; 加法运算符。 |
| - | 相减; 减法运算符。 |
| * | 标量和矩阵乘法运算符。 |
| .* | 阵列乘法运算符。 |
| ^ | 标量和矩阵求幂运算符。 |
| .^ | 阵列求幂运算符。 |
| \ | 左除法运算符。 |
| / | 右除法运算符。 |
| .\ | 阵列左除法运算符。 |
| ./ | 右除法运算符。 |
| : | 冒号; |
| 生成规则间隔的元素,并表示整个行或列。 | |
| ( ) | 括号; |
| (1)和函数一起使用,用于函数后面,用于包含函数的参数 | |
| (2)用于数组元素的索引; | |
| (3)覆盖优先级。 | |
| [ ] | 括号; |
| 罩住阵列元素,创建数组和矩阵时候使用。 | |
| . | 小数点。 |
| … | 省略号; 行连续运算符 |
| , | 逗号; |
| 分隔一行中的语句和元素 | |
| ; | 分号; |
| (1)用于矩阵内元素的换行; | |
| (2)用于屏幕的抑制输出显示。 | |
| % | 百分号;指定一个注释并指定格式。 |
| _ | 引用符号和转置运算符。 |
| ._ | 非共轭转置运算符。 |
| = | 赋值运算符。 |
运算的优先级规则:
(1)同等优先级下从左向右运算.
(2)优先级顺序(从高到低)
括号 ( )
乘方 ^
乘除法 * , /
加减法 + , -
程序一 :
例:长任务可以通过使用省略号( ... )扩展到另一行
initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity ...
+ acceleration * time
这些函数的对象可以是:数、数组、矩阵
函数分类
|
函数名 |
说明 |
指数函数 |
exp |
以e为底数 |
对数函数 |
log |
自然对数,即以e为底的对数 |
log10 |
常数对数,即以10为底的对数 | |
log2 |
以2为底的对数 | |
| 绝对值函数 | abs | 表示实数的绝对值及复数的模 |
| 三角函数(自变量的单位为弧度) | sin | 正弦函数 |
| cos | 余弦函数 | |
| tan | 正切函数 | |
| cot | 余切函数 | |
| sec | 正割函数 | |
| csc | 余割函数 | |
| ...... | ...... | ...... |
| 最大/最小函数 | max | 求最大数 |
| min | 求最小数 |
附表:MATLAB内置的三角运算函数大全
正弦: sin,sind,sinpi,asin,asind,sinh,asinh
余弦: cos,cosd,cospi,acos,acosd,cosh,acosh
正切: tan,tand,atan,atand,atan2,atan2d,tanh,atanh
余割: csc,cscd,acsc,acscd,csch,acsch
正割: sec,secd,asec,asecd,sech,asech
余切: cot,cotd,acot,acotd,coth,acoth
斜边: hypot
转换: deg2rad,rad2deg,cart2pol,cart2sph,pol2cart,sph2cart
MATLAB内置的指数对数函数:
exp,expm1,log,log10,log1p,log2,nextpow2,nthroot,pow2,reallog,realpow,realsqrt,sqrt
MATLAB内置的复函数: abs,angle,complex,conj,cplxpair,i,imag,isreal,j,real,sign,unwrap
例:
: 2.5^(-1.2)
: 3^0.5 或 sqrt(3)
: exp(2)
: log( exp(1)^0.5+3/sqrt(2) )
作业:上机编程计算下面表达式的值。

======================================
MATLAB常用命令:
clear 清空内存
clear all 清空全部内存
clc 清空屏幕
help max 查看max函数的基本用法(当然,你可以把max换成其他你想查看的函数)
doc max 查看max函数的详细使用文档(当然,你可以把max换成其他你想查看的函数)
whos 查看内存中所有变量的详细情况
whos x,y 查看指定的变量x,y的详情(当然你可以改为其他你想查看的变量名)
class x 查看变量x的属性,也就是属于哪种变量类型。
======================================
拓展知识1:
编译器与自举
1个很有意思的问题:
C语言的编译器,是用C语言写的!
什么?C语言是用C语言写的,这不就是“鸡生蛋,蛋生鸡”的问题吗?
要让C语言编译通过,就需要一个C语言编译器。但是C语言编译器是用C写的。那么世界上第一个能执行的编译器,是如何编译的呢?
这种编译器也用语言本身写的特性,称之为“自举”。
奇怪的是,这么一个让我们纳闷的问题,却很少有人提到。似乎大神们觉得很自然,不屑于说明。
直到后来学到一些编译相关的技术,才慢慢了解到这件事的原委。原因不复杂,我简化一下表述:
首先,简化C语言的设计,只选择最最基本、不得不实现的功能,形成一个C语言的子集。我们可以叫它C0。
用汇编语言实现C0语言的编译器,由于C0功能很少,比较容易直接写一个编译器。
用C0语言去实现更多必要的功能,由于C0语言功能太弱,遇到不好写的地方可以用汇编来打补丁。最终你得到了一个改进版的C0语言,我们称之为C1。
用C1语言去继续实现更多C语言功能,不好写的地方继续用汇编打补丁。可以得到C2语言
用C2语言去继续实现更多C语言功能,不好写的地方继续用汇编打补丁。可以得到C3语言
以此类推……
到Cn语言的时候,你已经得到了一个足够接近C语言的编译器。
继续迭代一两次……
终于,你得到了一份C语言的编译器。而前面的从C0版到Cn-1 版的编译器,都可以扔掉了。
为什么要分N个步骤呢?主要还是为了解释C语言慢慢进化的历史过程。实际上不见得要分很多步,很多中间步骤只是代表了远古大神们迭代改进的过程。
如果大神足够神,可以更简化:
直接用汇编语言写一个C语言编译器。
然后再用C语言写一个C语言编译器的源码,用汇编版的编译器 编译这个C代码
即可得到一个可运行、可正常使用的编译器。
然后,那个用汇编语言写的版本就可以扔掉了。
理解这个问题的关键,是认识到:编译器,只是读取文本文件(源代码),输出某种计算机编码(比如机器语言)的程序。
既然编译器也只是个普通的程序,那么就能用任何语言编写。
所以,理论上来讲,你可以用Python、Java或者Scratch来写个C语言编译器
理论上,编译器只是把文本文件编译成二进制代码,因此,任何语言都可以用来写编译器,比如c语言是1972年诞生的,basic语言比他早,用basic语言写个c语言的编译器也不是不可以。当然,实际情况是c语言的第一个版本是用b语言加汇编写成的,b语言本身是汇编语言写成的,汇编语言是机器语言。现在写编译器大多用c++写。
拓展知识2:浮点数与定点数
首先,计算机的小数并不都叫浮点数。
只是现代桌面处理器大都集成有 FPU (浮点处理器),我们在写程序时,用到小数的地方,用 float 类型表示,可以方便快速地对小数进行运算。
计算机中小数的表示法,其实有定点和浮点两种。
定点表示法因其难以避免的局限性 (表示范围和精度是一对矛盾体),已经被当代桌面处理器(如x86)摒弃不用。但我想只要你愿意,依然可以在你台式机的编译器中用定点开心的玩着小数。
但是,并不是所有的处理器都像 X86 这么豪,在某些恶劣、简陋的嵌入式环境中,哪有 FPU 给你用,小数还是不得不用定点的方式,例如某些 DSP。因为定点运算相对浮点较为简单。
科普到底,以 32 bit 机器为例,说下什么是定点数和浮点数。
定点数
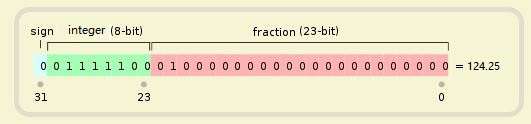
定点的意思是,小数点固定在 32 位中的某个位置,前面的是整数,后面的是小数。
小数点具体固定在哪里,可以自己在程序中指定。
例如上面的例子,小数点在 23 bit 处。
无论你是124.25,是0.5, 还是100, 小数点都在 23 bit 的位置固定不变。
浮点数
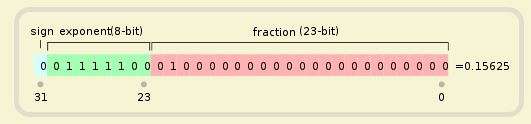
浮点数的存储格式,一般按照标准 IEEE 754。
IEEE 754 规定,浮点数的表示方法为:
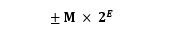
最高的 1 位是符号位 s,接着的 8 位是指数E,剩下的 23 位为有效数字 M。
例如:
5 DEC = 101 BIN = 1.01 x 2^2
9 DEC = 1001 BIN = 1.001 x 2^3
100 DEC = 01100100 BIN = 1.100100 x 2^6
0.125 DEC = 0.001 BIN = 1 x 2^-3
这一下,小数点的位置就是迷之存在,漂浮不定了。
浮点,想必故此得名吧。
浮点数的底层表示
浮点数的精度损失问题
浮点数的表示范围和精度
浮点数的表示借鉴了科学计数法,比如在十进制中 可以表示成
。类似地,浮点型数据的二进制存储结构也可以被划分成:符号位 + 指数位 + 尾数位。按照国际标准IEEE 754,任意一个二进制浮点数可以表示成:
其中:
表示符号位,
表示正数,
表示负数
表示有效数字,
表示指数位
指数部分决定了数的大小范围,有效数字部分决定了数的精度。
举两个简单的例子:
| 十进制 | 二进制 | 二进制科学计数法 | S | E | M |
|---|---|---|---|---|---|
| 3.0 | 11.0 | 1.1 x 2^1 | 0 | 1 | 1.1 |
| -5.0 | -101.0 | -1.01 x 2^2 | 1 | 2 | 1.01 |
double类型和float类型(可能还有long double类型)在计算机的底层存储结构都是一致的,唯一的不同在于float是32位而double是64位的。
无论什么数据,在计算机内存中都是以01存储的,浮点数也不例外。
计算机中小数的表示按照小数点的位置是否固定可以分为浮点数和定点数。为了方便和float32浮点数做对比,我们构造一个32位精度的定点数,其中小数点固定在23bit处:

从定点数的存储上看,它表示的数值范围有限(以小数点在23bit为例,整数部分仅有8位,则整数部分取值范围是0~255),但好在处理定点数计算的硬件比较简单。
以32位浮点数为例,最高一位是符号位s,接着的8位是指数位E,最后的23位是有效数字M。double64最高一位是符号位,有11个指数位和52个有效数字位。下图展示了float32类型的底层表示:
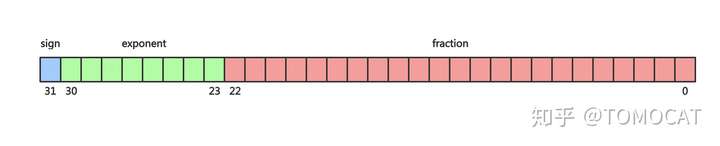
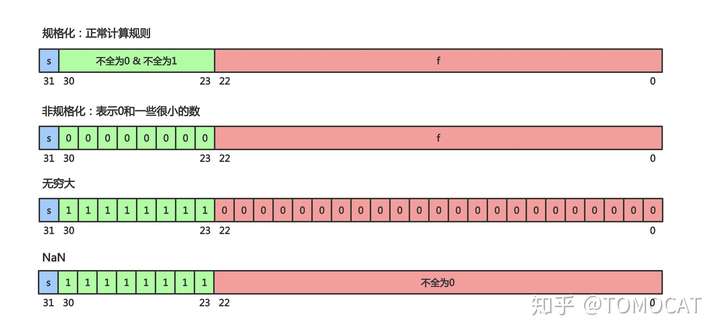
其中IEEE 754的规定为:
因为M的取值一定是1<=M<2,因此规定M在存储时舍弃第一个1,只存储小数点之后的数字,这样可以节省存储空间(以float32为例,可以保存23位小数信息)
指数E是一个无符号整数,因此它的取值范围为0255,但是指数可以是负的,所以规定在存入E时在它原本的值加上127(使用时减去中间数127),这样E的取值范围为-127128
E不全为0,不全为1:正常的计算规则,E的真实值就是E的字面值减去127(中间值),M加回1
E全为0:指数E等于1-127为真实值,M不加回1(此时M为0.xxxxxx),这样是为了表示0和一些很小的数
E全为1:M全为0表示正负无穷大(取决于S符号位);M不全为0时表示不是一个数(NaN)
以78.375为例,它的整数和小数部分可以表示为: 因此二进制的科学计数法为:
一般而言转换过程包括如下几步:
改写整数部分:将整数部分的十进制改写成二进制
改写小数部分:拆成 到
的和
规格化:保证小数点前只有一位是1,改写成二进制的科学计数法表示
填充:指数部分加上127(中间数)填充E;有效数字部分去掉1后填充M
按照前面IEEE 754的要求,它的底层存储为:

十进制中的0.5(代表分数1/2)表示二进制中的0.1(等同于分数1/2),我们可以把十进制中的小数部分乘以2作为二进制的一位,然后继续取小数部分乘以2作为下一位,直到不存在小数为止。
以0.2这个无法精确表示成二进制的浮点数为例:
因此十进制下的0.2无法被精确表示成二进制小数,这也是为什么十进制小数转换成二进制小数时会出现精度损失的情况。
单精度浮点数float占四个字节,表示范围-3.40E+38 ~ +3.40E+38
双精度浮点数double占八个字节,表示范围-1.7E+308 ~ +1.79E+308
以float为例,能表示的最大二进制数据为(小数点后为23个1),而二进制下
,因此能表示的最大十进制数据是:
从二进制小数的科学计数法表示上看,可以知道float的精度为 ,double的精度为
。
[1] https://q.115.com/182920/T1268124.html
[2] https://blog.csdn.net/u014470361/article/details/79820892
[3] https://www.cnblogs.com/wangsiting1997/p/10677805.html
[4] https://blog.csdn.net/u014470361/article/details/79820892
[5] https://www.cnblogs.com/yiyide266/p/7987037.html
拓展知识3:matlab中的eps函数详解
使用matlab在写代码过程中遇到了除数为0的情况,在分母位置加了eps就没有报错了!
首先matlab中eps是一个函数,可以返回某一个数N的最小浮点数精度,形式例如eps(N)。eps(a)是|a|与大于|a|的最小的浮点数之间的距离,距离越小表示精度越高。
默认a=1,即eps = eps(1); 我们在matlab中敲入eps和eps(1)可以发现结果是一样的。eps = eps(1) = 2.2204e-16。
eps为系统运算时计算机允许取到的最小值。例如对于函数y=cosx/x。由于在编程时分母可能出现为0,所以编程时要写成:y=cosx/(x+eps)。
下来解释下eps:
我们知道浮点数其实是离散的,有限的,而且间隔是不均匀的。我们可以说一个数旁边的数是什么,而它们之间的距离就反应了其精度。越靠近0,数和数之间就越密集,精度就越高。
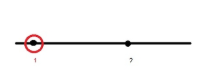
我画了一个简图,黑色实心点代表的是数轴的数,例如1,红圈与1的距离代表的就是eps(1),那么在1+eps(1)/2到1之间的所有数,都被认作1,MATLAB无法识别介于1和1+eps(1)/2之间的数。
例一,eps(1)


可以发现eps=eps(1)=2.2204e-16,由于matlab无法区分1到1+eps(1)/2之间的数,所以就将中间的这些数四舍五入到1或者1+eps(1),比如上图中,1+0.3eps(1)就被舍入到1,然后大于0.5时,1+0.7eps(1)就被近似为1+eps(1)。
例二,eps(0)

我们可以看到eps(0)比eps(1)小很多,别的精度和1一样,在0到eps(0)*0.5之间的所有数都是0,eps(0)*0.5以上到eps(0)之间的所有数都被近似为eps(0)。
例三,eps(2)以及eps(N)

我们可以发现最小精度eps(N)随着数量级增大,eps也在逐渐增大,这在计算的过程中,都要注意。防止大数吃小数。
float与“零值”比较 一般情况我们会定义一个很小的接近于0的值比如0.00001或者更小的,然后浮点数跟这个数作比较。
float与float比较