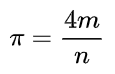运算符是一个符号，它告诉编译器执行特定的数学或逻辑操作。 MATLAB主要用于整个矩阵和阵列的操作。因此，MATLAB中的运算符既可用于标量数据也可用于非标量数据。MATLAB允许以下类型的基本操作
算术运算符
关系运算符
逻辑运算符
按位运算符
集合运算符
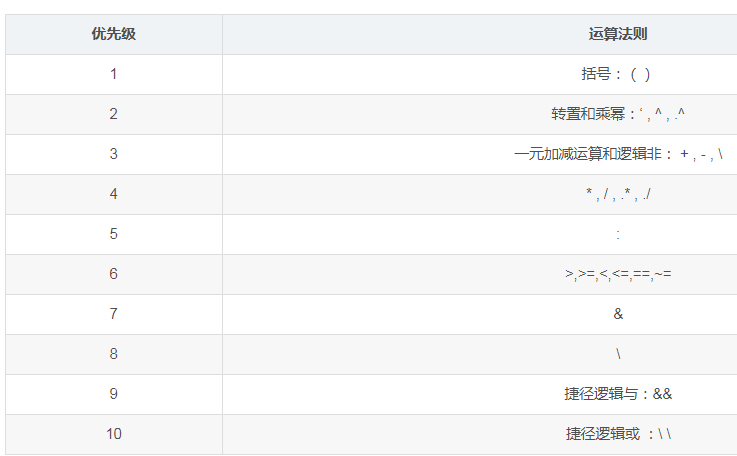
MATLAB中运算优先级排列
1、算术运算
MATLAB允许两种不同类型的算术运算 -
矩阵算术运算
数组算术运算
矩阵算术运算与线性代数中定义的相同。在一维和多维数组中，逐个元素执行数组运算。
矩阵运算符和数组运算符由句点符号(.)区分。 然而，由于对于矩阵和阵列的加减运算是相同的，因此对于这两种情况，运算符相同。
下表为常用的四则运算符详解：
| 运算符 | 描述说明 |
| + | 加法或一元加法运算。A + B表示相加存储在变量A和B中的值。A和B必须具有相同的大小，除非是标量。 标量可以添加到任何大小的矩阵。 |
| - | 减法或一元减法运算。 A-B表示从A中减去B的值。A和B必须具有相同的大小，除非是标量。可以从任何大小的矩阵中减去标量。 |
| * | 矩阵乘法。 C = A * B是矩阵A和B的线性代数乘积。更准确地说，执行公式： |
| |
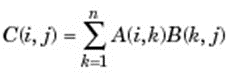
| .* | 阵列乘法。 A .* B是数组A和B的逐个元素乘积。A和B必须具有相同的大小，除非它们之一是标量。 |
| / | 数组乘法。A .* B是数组A和B的逐个元素乘积。A和B必须具有相同的大小，除非它们之一是标量。 |
| ./ | 数组右除。A./B是具有元素A(i，j)/ B(i，j)的矩阵。 A和B必须具有相同的大小，除非它们之一是标量。 |
| \ | 反斜杠或数组左除。如果A是一个方阵，A B与inv(A)* B大致相同，除了以不同的方式计算。如果A是n×n矩阵，B是具有n个分量的列向量或具有若干这样的列的矩阵，则X = A B是方程AX = B的解。如果A是不规则或几乎单数，将显示警告消息。 |
| .\ | 阵列左除。A . B是具有元素B(i，j)/ A(i，j)的矩阵。A和B必须具有相同的大小，除非它们之一是标量。 |
| ^ | 矩阵 X ^ p是X的P次幂，如果p是标量。 如果p是整数，则通过重复平方来计算幂值。 如果整数为负，则X首先倒置。 对于p的其他值，计算涉及特征值和特征向量，使得如果[V，D] = eig(X)，则X ^ p = V * D. ^ p / V。 |
| .^ | 阵列幂值， A ^ B是B(i，j)到A(i，j)的幂矩阵。A和B必须具有相同的大小，除非它们之一是标量。 |
| ' | 矩阵转置。 '是A的线性代数转置。对于复数矩阵，这是复共轭转置。 |
| .' | 数组转置。.'是A的数组转置。对于复数矩阵，这不涉及共轭。 |
1)加减运算
A=[1,2 ; 3,4];
B=[5,6 ; 7,8];
x1=A+B
x2=A-B
x1 =
6 8
10 12
x2 =
-4 -4
-4 -4
2)乘法
A=[ 2 5 7
1 3 6
3 2 5 ];
B=[ 1 3 5
2 4 6
5 6 7 ];
c1=A*B %矩阵相乘必须有A为[m,n],B为[n,p]矩阵,即为A的列数需要和B的行数相等.
c2=B*A
c3=A.*B
c1 =
47 68 89
37 51 65
32 47 62
c2 =
20 24 50
26 34 68
37 57 106
c3 =
2 15 35
2 12 36
15 12 35
3)除法
%矩阵的除法分为左除和右除,
% A\B=inv(A)*B
% B/A = B*inv(A)
a=[ 11 5 3;
78 5 21;
7 15 9 ];
b=[ 20 30 40;
30 40 50 ;
40 50 60 ];
c1=a\b
c2=b/a
c3=b./a
d1=inv(a)*b
d2=b*inv(a)
%比较c1,d1和c2,d2,既可以看到是否相等.
c1 =
0.7692 1.5385 2.3077
3.6923 5.7179 7.7436
-2.3077 -5.1709 -8.0342
c2 =
-9.9786 1.2222 4.9188
-11.3034 1.4444 5.9530
-12.6282 1.6667 6.9872
c3 =
1.8182 6.0000 13.3333
0.3846 8.0000 2.3810
5.7143 3.3333 6.6667
d1 =
0.7692 1.5385 2.3077
3.6923 5.7179 7.7436
-2.3077 -5.1709 -8.0342
d2 =
-9.9786 1.2222 4.9188
-11.3034 1.4444 5.9530
-12.6282 1.6667 6.9872
4)矩阵的乘方
%乘方的要求为:A^x,其中A为方阵,x为标量.
A=[3 0 7; 9 12 8; 1 5 3];
result = A^3 %A为方阵,x为标量.
result =
405 630 518
2268 3123 3022
884 1180 1125
5)点运算
% 点运算分为： .* ， ./ ， . ， .^
%【两个矩阵进行点运算】是指对应元素进行运算。
%A.*B 指的是对应元素相乘.
%A./B 表示对应元素相除
%A.^B表示对应元素做乘方运算.
%【要求】两矩阵具有相同的维数。
A = [1 3 5 ; 2 4 6 ; 3 6 9]
B = [9 10 7 ; 6 9 4 ; 2 5 8]
C=A.*B % A.*B 指的是对应元素相乘.
% A./B == B.A
C1=A./B %A./B 表示对应元素相除
C2=B.A
x=[2 2 2 ]
y=[1 2 3 ]
z=x.^y %x.^y表示对应元素做乘方运算.
A =
1 3 5
2 4 6
3 6 9
B =
9 10 7
6 9 4
2 5 8
C =
9 30 35
12 36 24
6 30 72
C1 =
0.1111 0.3000 0.7143
0.3333 0.4444 1.5000
1.5000 1.2000 1.1250
C2 =
0.1111 0.3000 0.7143
0.3333 0.4444 1.5000
1.5000 1.2000 1.1250
x =
2 2 2
y =
1 2 3
z =
2 4 8
例 ：当x=1,3,5,7,9时,分别求y=x^2*cos(x)的值.
x=1:2:9
y=x.^2.*cos(x)
x =
1 3 5 7 9
y =
0.5403 -8.9099 7.0916 36.9412 -73.8016
2、逻辑运算
真或假（布尔）条件logical数据类型分别使用数字 1和 0代表 true或 false 状态。
某些 MATLAB函数和运算符返回逻辑值以指示是否满足某个条件。可以使用这些逻辑值作为数组索引或执行条件代码。
| & | “与”逻辑 AND |
| ~ | “非”逻辑 NOT |
| | | “或”逻辑 OR |
| xor | “异或”逻辑 xor |
| all | 确定所有的数组元素是为非零还是 true |
| any | 确定任何数组元素是否为非零 |
| FALSE | 逻辑 0（假） |
| find | 查找非零元素的索引和值 |
| islogical | 确定输入是否为逻辑数组 |
| logical | 将数值转换为逻辑值 |
| TRUE | 逻辑值 1（真） |
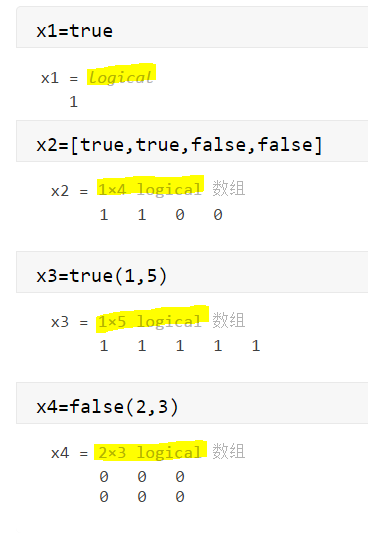
1）逻辑数据的生成
例：true、false来生成逻辑数据
x1=true
x2=[true,true,false,false]
x3=true(1,5)
x4=false(2,3)
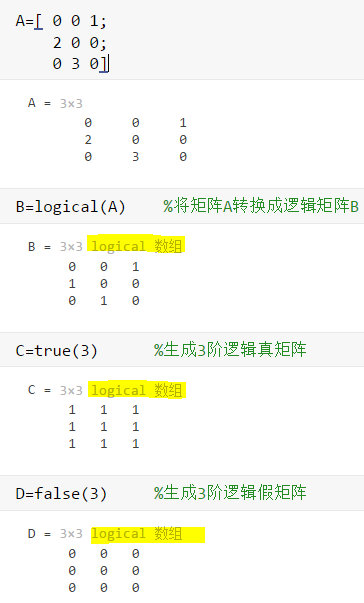
例：使用函数logical( ) 把数值型数据转换为逻辑型数据，
注意：logical( ) 函数的转换规则是 “非零数字转为逻辑1，数字0转换成逻辑0”
A=[ 0 0 1;
2 0 0;
0 3 0];
B=logical(A) %将矩阵A转换成逻辑矩阵B
C=true(3) %生成3阶逻辑真矩阵
D=false(3) %生成3阶逻辑假矩阵
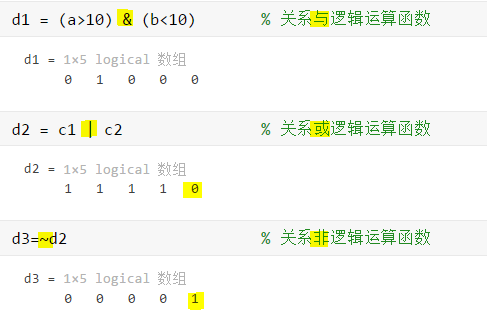
2）基本逻辑运算——与或非（&,|,~）运算
例：
3）异或运算xor
异或的数学符号为“⊕”，其运算法则为：a⊕b = (¬a ∧ b) ∨ (a ∧¬b)，在MATLAB中采用xor来实现。
如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。
>> x=[1 0 0 1 0 1 0];
>> y=[1 0 1 0 1 1 1];
>> z=xor(x,y)
z =
1×7 logical 数组
0 0 1 1 1 0 1
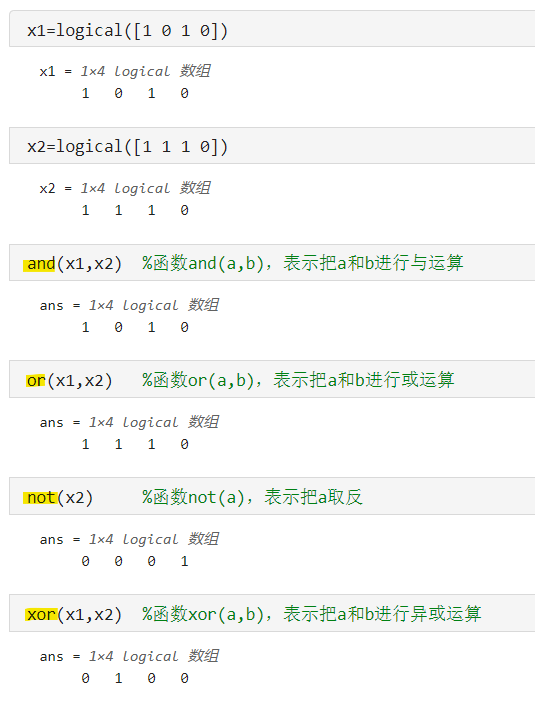
也可以使用函数“and( )、or( )、 not( )、xor( )”进行逻辑与或非等运算，如：
x1=logical([1 0 1 0])
x2=logical([1 1 1 0])
and(x1,x2) %函数and(a,b)，表示把a和b进行与运算
or(x1,x2) %函数or(a,b)，表示把a和b进行或运算
not(x2) %函数not(a)，表示把a取反
xor(x1,x2) %函数xor(a,b)，表示把a和b进行异或运算
运行结果：
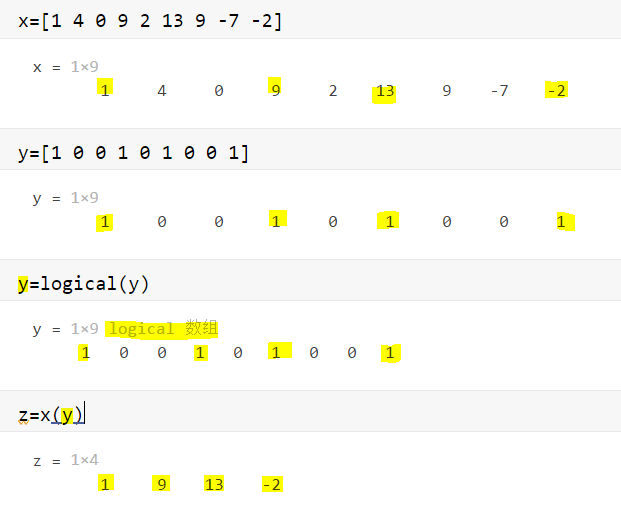
4）逻辑索引
注意：采用逻辑索引时，逻辑数组的size要和被索引的数组的size一致。
例：数组的逻辑索引
例，矩阵的逻辑索引-1：
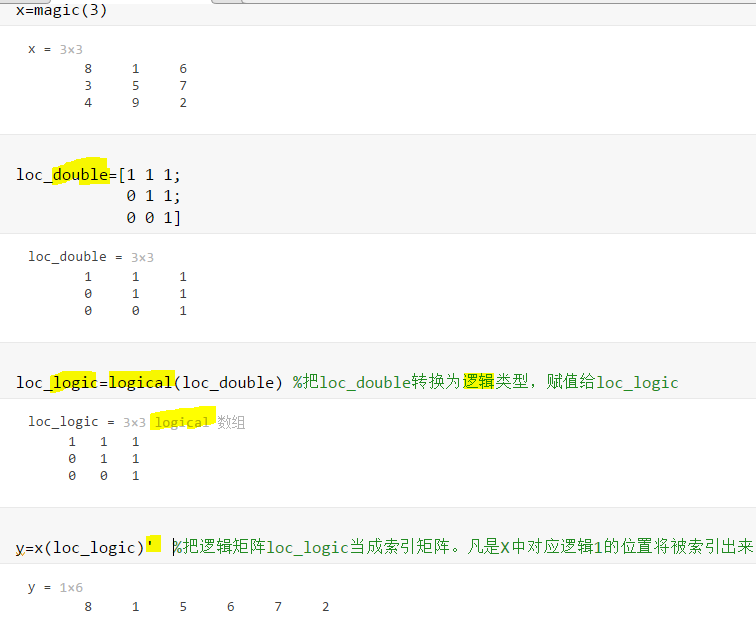
练习：把magic(5)矩阵的十字架上的元素索引出来。
x=magic(5)
y=[ 0 0 1 0 0 ;
0 0 1 0 0;
1 1 1 1 1;
0 0 1 0 0;
0 0 1 0 0];
y=logical(y)
z=x(y)'
例：给定任意一个随机数组，如何把奇数位置的元素索引出来？
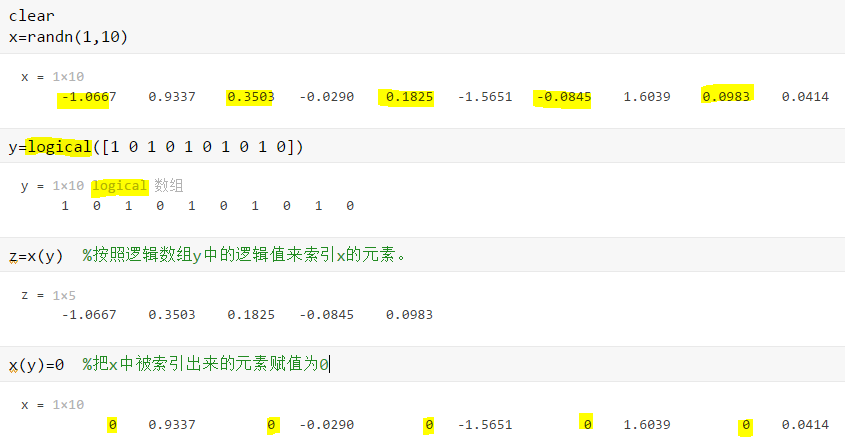
上述代码的改进型：
clear
x=randn(1,100)
y1=[1 0]
y2=repmat(y1,1,50)
y3=logical(y2)
x(y3)
课堂练习：对数组 x=randn(1,100) ，从第1个元素开始往后数，每数6个元素作为一组，索引出第一个，把这些索引出来的元素组成数组z,并求数组z所有元素之和。要求：使用两种方法来做，分别用普通的下标索引法，以及逻辑索引法。
%方法1 下标法
x=randn(1,100)
y=1:6:100
z=x(y)
sum(z)
%方法2 逻辑索引法
x=randn(1,100)
a=[1 0 0 0 0 0];
b=[1 0 0 0];
y1=repmat(a,1,16)
y2=[y1 , b]
y3=logical(y2)
z=x(y3)
sum(z)
3、关系运算
关系运算符比较两个数组中的元素，关系运算符也可以用于标量和非标量数据。数组的关系运算符在两个数组之间执行逐个元素的比较，并返回相同大小的逻辑数组，如果为真，则元素设置为逻辑1(true)，如果为假，则元素设置为逻辑0(false)。
| == | 确定相等性 |
| >= | 确定大于或等于 |
| > | 确定大于 |
| <= | 确定小于等于 |
| < | 确定小于 |
| ~= | 确定不相等性 |
| isequal | 确定数组相等性 |
| isequaln | 测试数组相等性，将 NaN 值视为相等 |
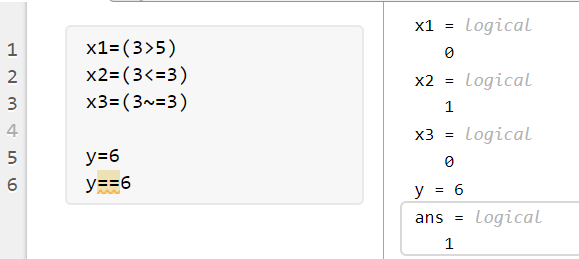
例：两个元素之间的关系运算：
例: 两个矩阵之间的关系运算（运算时，两个矩阵内对应元素之间做运算）
a=[1 2 ; 3 4]
b=[1 3 ; 2 4]
c1 = a>b %矩阵对应元素比较
c2 = a==b
c3 = a~=b
c4 = a<b
c5 = a<=b
c6 = a>=b
d = a(c2) %取出a中和b相等的元素.
例：数组/矩阵 和单个元素的比较
例：
>> str1='aabcdaxa'
str1 =
'aabcdaxa'
>> 'a'==str1 %相当于用字符'a'去和str1中的每一个字符进行比较。
ans =
1×8 logical 数组
1 1 0 0 0 1 0 1
>> str1('a'==str1)='@' %所有逻辑1的位置被选中，然后用字符'@'替换。
str1 =
'@@bcd@x@'
例：：
A = [0 -1 4
9 -14 25
-34 49 64]；
B = A < 0 %返回一个零一矩阵，数组A中元素小于0的对应位置为1
A(B) =0 %将数组B指定位置值置为0
运行上述代码：
B =
3×3 logical 数组
0 1 0
0 1 0
1 0 0
A =
0 0 4
9 0 25
0 49 64
注意：使用==对两个数字进行比较时，如果使用double类型，则当两个数字不同但又非常接近时（如小数点前15位一致，而第16位开始不一样），系统会认为两者相等。如以下代码：
所以，使用“==”运算时，使用int类型可以避免上述错误。x1=1.01
y1=1.0100000000000001
z1=(x1==y1) %返回逻辑1，因为差距过小，认为两者相等。
x2=1.01
y2=1.010000000000001
z2=(x2==y2) %返回逻辑0，认为两者不相等。
课堂练习1：对随机矩阵a=randn(10,10),如何计算矩阵a中处于-1到+1之间的元素总数目？
课堂练习2: 模拟50个同学某门课的期末成绩（随机分布在30-100之间），找出不及格的人数，以及占班级总人数的百分比。再把50-59分的分数置为60。
4、按位运算
按位运算符对位执行，并执行逐位运算。＆，|和^的真值表如下 -
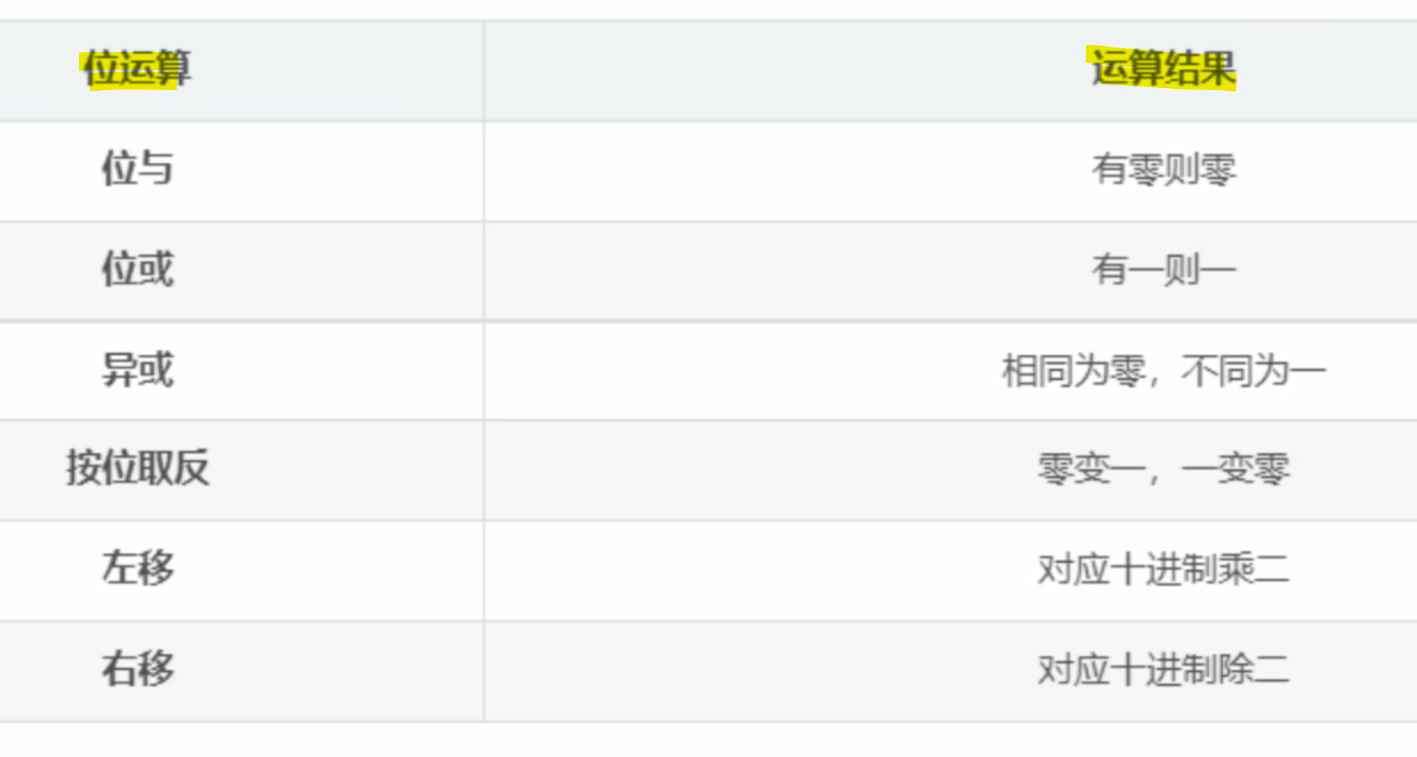
假设 A = 60 和 B = 13 ; 现在以二进制格式，它们将如下所示：
A = 0011 1100
B = 0000 1101
%-------------------
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A = 1100 0011MATLAB提供了诸如“按位与”和“按位或”以及“按位非”操作，移位操作等位操作的各种功能。下表显示了常用的按位操作：
| 方法 | 目的 |
|---|---|
| bitand(a, b) | 整数a和b的位与AND操作 |
| bitcmp(a) | a的比特补码 |
| bitget(a,pos) | 在整数数组a中，获取指定的位置pos位字节 |
| bitor(a, b) | 整数a和b的逐位OR操作 |
| bitset(a, pos) | 设置在指定pos处的位字节 |
| bitshift(a, k) | 返回向左移位k字节，相当于乘以2^k。 k 的负值对应于向右移位或除以` 2^k ` 并舍入到最接近的整数到负无穷大。任何溢出位都被截断。 |
| bitxor(a, b) | 整数a和b的逐字节位XOR操作 |
| swapbytes | 交换字节排序 |
&&和|| 与 &和| 的区别？
单个＆符是逻辑AND运算符。双＆符&&还是一个逻辑AND运算符，采用短路行为。短路仅表示仅当第一个操作数（左侧）未完全确定结果时才评估第二个操作数（右侧）
&是逻辑AND运算符，&&是短路AND运算符。它们在操作数的求值方式以及是否对数组或标量进行操作方面有所不同：&（AND运算符）和|（OR运算符）可以按元素方式对数组进行运算。与其他语言类似，&是逻辑按位运算符，&&而是逻辑运算。
&&和||是短路版本，仅当结果未完全由第一个操作数确定时才评估第二个操作数。它们只能在标量上运行，而不能在数组上运行。
对于&&，仅当左操作数为true时才计算右操作数，并且结果是单个布尔值。如：x = (b ~= 0) && (a/b > 18.5)
5、集合运算
MATLAB为集合操作提供了各种功能，如联合，交集和集合成员的测试等。
| 函数 | 描述 |
|---|---|
| intersect(A,B) | 设置两个阵列的交集; 也就是返回A和B 共同的值。返回的值按排序顺序排列。 |
| intersect(A,B,’rows’) | 将A的每一行和B的每一行视为单个实体，并返回A 和B两者共同的行。返回矩阵的行按排序顺序排列。 |
| ismember(A,B) | 返回与A相同大小的数组，其中包含1(true)，其中A的元素位于B中。其他地方返回0(false)。 |
| ismember(A,B,’rows’) | 将A的每行和B的每一行视为单个实体，并返回一个包含1(true)的向量，其中矩阵A的行也是B 行。其他返回0(false)。 |
| issorted(A) | 如果A的元素按排序顺序返回逻辑1(真)，否则返回逻辑0 (假)。输入A可以是一个向量，也可以是N-by-1 或1-by-N的字符串数组。 如果A和sort(A) 的输出相等，则认为A被排序。 |
| issorted(A, ‘rows’) | 如果二维矩阵A的行按排序顺序返回逻辑1(真)，否则返回逻辑0(假)。 如果A和排序(A)的输出相等，则认为矩阵A被排序。 |
| setdiff(A,B) | 设置两个数组的差异; 返回A中不在B中的值。返回的数组中的值按排序顺序排列。 |
| setdiff(A,B,’rows’) | 将A的每一行和B的每一行视为单个实体，并从不在B中的A返回行。返回的矩阵的行按排序顺序排列。'rows'选项不支持单元格数组。 |
| setxor | 设置两个数组的异或 |
| union | 设置两个数组的并集 |
| unique | 使数组中的值唯一 |
例：
A = [7 1 7 7 4];
B = [7 0 4 4 0];C = intersect(A,B)C = 1×2
4 7
A = [3 6 2 1 5 1 1];
B = [2 4 6 8];
C = setdiff(A,B) %相当于A-B
C = 1×3
1 3 5
A = [5 7 1 7];
B = [3 1 1 5];C = union(A,B)C = 1×4
1 3 5 7
A = [9 2 9 5 2 5];C = unique(A)C = 1×3
2 5 9
6、排列组合运算
C = nchoosek(n,k) 其中n和k是非负整数, 返回 n!/((n–k)! k!).
这是从n种情况中一次取出k种的组合的数量。比如，从全班30个同学里抽出10个同学参加某个活动，有多少种选法？
>> nchoosek(30,10)
ans =
30045015
C = nchoosek(v,k), 其中v是一个长度为n的行向量，创建一个矩阵，该矩阵的行由每次从v中的n个元素取出k个取值的所有可能组合构成。
矩阵 C 包含 n!/((n–k)! k!) 行和 k 列.
输入 n, k, 和 v 支持类型：float double 和 float single.
例子：>> v=[1 3 5 7 9];
>> y=nchoosek(v,3)
y =
1 3 5
1 3 7
1 3 9
1 5 7
1 5 9
1 7 9
3 5 7
3 5 9
3 7 9
5 7 9
>> v2='abcd';
>> y2=nchoosek(v2,3)
y2 =
4×3 char 数组
'abc'
'abd'
'acd'
'bcd'
（2）排列函数: perms()
P = perms(v)返回的矩阵包含了向量 v中元素按字典顺序反序的所有排列。P的每一行包含 v中 n 个元素的一个不同排列。矩阵 P具有与 v相同的数据类型，包含 n! 行和 n 列。
>> v=[1 3 0 -2];
>> y=perms(v)
y =
-2 0 3 1
-2 0 1 3
-2 3 0 1
-2 3 1 0
-2 1 0 3
-2 1 3 0
0 -2 3 1
0 -2 1 3
0 3 -2 1
0 3 1 -2
0 1 -2 3
0 1 3 -2
3 -2 0 1
3 -2 1 0
3 0 -2 1
3 0 1 -2
3 1 -2 0
3 1 0 -2
1 -2 0 3
1 -2 3 0
1 0 -2 3
1 0 3 -2
1 3 -2 0
1 3 0 -2
>> whos y
Name Size Bytes Class Attributes
y 24x4 768 double
其他逻辑操作运算：
1.all ，若向量的所有元素都非零,结果为1，否则为0
resultALL = all( [10 20 30 40 ] ) %均非零,结果为1.
resultALL =
1
2.any ，若向量中有一个以上的元素非零,结果为1；只有所有元素都是0时结果才为0
resultANY = any([1 2 3 4 5 0]) %有元素非零,结果为1.
resultANY =
1
3.exist 判断工作空间是否存在,存在为1,否则非零.
resultEXIST = exist('plot')
resultEXIST =
5
4.find 找出向量或矩阵非零元素的位置
find函数：查询非零元素的位置和值
用法1：B = find(A)，A是一个矩阵，查询（按列）非零元素的位置;
如果A是一个行向量，则返回一个行向量，否则，返回一个列向量。
如果A全是零元素或者空数组，则返回一个空数组。
>> A = [0 1 2 0 4 5]
A =
0 1 2 0 4 5
>> B = find(A)
B =
2 3 5 6
>> A = [0 1 2 ; 0 4 5]
A =
0 1 2
0 4 5
>> B = find(A)
B =
3
4
5
6
(位置的判定：在矩阵中，第一列开始，自上而下，依次为1，2，3...,
然后再从第二列，第三列依次往后数)
用法2：B = find(A>2)，找到A中比2大的元素的位置
>> A = [0 1 2 ; 0 4 5]
A =
0 1 2
0 4 5
>> B = find(A>2)
B =
4
6
用法3：B = find(A，2)，找到A中最先出现的2个不为零的数的位置
>> A = [0 1 2 ; 0 4 5 ; 6 0 8]
A =
0 1 2
0 4 5
6 0 8
>> B = find(A, 2)
B =
3
4
用法4：B = find(A，2, 'first')，找到A中最先出现的2个不为零的数的位置
B = find(A，2, 'last')，找到A中最后出现的2个不为零的数的位置
>> A = [0 1 2 ; 0 4 5 ; 6 0 8]
A =
0 1 2
0 4 5
6 0 8
>> B = find(A, 2, 'first')
B =
3
4
>> C = find(A,2,'last')
C =
8
9
用法5：[x, y] = find(A)，找到A中非零元素所在的行和列，
行存储在矩阵x中，列存储在矩阵y中
用法6：[x, y, v] = find(A)，找到A中非零元素所在的行和列，
行存储在矩阵x中，列存储在矩阵y中，值存储在矩阵v中
（需要知道值的用此用法，其他用法只能确定位置）
5.isempty 判断矩阵是空矩阵 如果为空,则为1,非空0;
resultISEMPTY = isempty([1 2 3 ; 4 5 6 ; 7 8 9 ]) %矩阵显然非空,则为0
resultISEMPTY =
0
6.isglobal 判断是否为全局变量,是为1,非为0
7.isinf 判断是否为无穷小量,是为1,否为0
8.isnan 若元素是nan,则为1,否为0
9.isfinite 若矩阵大小有限,则取1,否则则为0
10. issparse 判断是否为稀疏矩阵,是为1,否为0
11. ischar 判断变量是字符组,是为1,否则取0
12、isequal函数，确定两个数组是否相等。
基本语法：
tf = isequal(A,B)
tf = isequal(A1,A2,...,An)
如果 A 和 B 等效，则 tf = isequal(A,B) 返回逻辑值 1 (true)；否则，返回逻辑值 0 (false)。
有关每种数据类型的等效性的定义，请参阅输入参数部分
13、isa（）函数，确定输入是否具有指定数据类型
语法：tf = isa(A,dataType) ； tf = isa(A,typeCategory)
说明：如果 A 具有 dataType 指定的数据类型，tf = isa(A,dataType) 将返回 1 (true)。
否则，将返回 0 (false)。输入参量 A 可以具有任何数据类型。
如果 A 是对象且 dataType 是 A 的类或 A 的超类，则 isa 返回 1。
示例：
创建数值变量并确定其数据类型是否为 double。
A = 3.1416;
tf = isa(A,'double')
tf = logical
1
创建一个 32 位整数数组，并确定其数据类型是否为 int32。
A = int32([0 2 4 6 8])
A = 1x5 int32 row vector
0 2 4 6 8
tf = isa(A,'int32')
tf = logical
1
确定 A 的数据类型是否为 char。
tf = isa(A,'char')
tf = logical
0
确定变量类型是否属于指定的类别
创建一个其数据类型为 uint8 的数组。确定该数组是否具有属于 integer 类别的数据类型。
A = uint8([0 2 4 6 8])
A = 1x5 uint8 row vector
0 2 4 6 8
tf = isa(A,'integer')
tf = logical
1
课后练习1：查看圆周率前10万位里面，是否包含自己的生日（如3月12日生日，则查看pi中是否有0312这个四个连续数字），如果有，返回自己生日处于小数点后面多少位？
>> s=vpa(pi,50000);
s=char(s);
>> strfind(s,'0312')
课后练习2：异或运算的应用
一个数组包含 n-1 个成员，这些成员是 1 到 n 之间的整数，且没有重复，请找出缺少的那个数字。
最快的解答方法，就是把所有数组成员（A[0] 一直到 A[n-2]）与 1 到 n 的整数全部放在一起，进行异或运算。
A[0] ^ A[1] ^ ... ^ A[n-2] ^ 1 ^ 2 ^ ... ^ n
上面这个式子中，每个数组成员都会出现两次，相同的值进行异或运算就会得到 0。只有缺少的那个数字出现一次，所以最后得到的就是这个值。
你可能想到了，加法也可以解这道题。
1 + 2 + ... + n - A[0] - A[1] - ... - A[n-2]
但是，加法的速度没有异或运算快，而且需要额外的空间。如果数字比较大，还有溢出的可能。
下面是一道类似的题目，大家可以作为练习。
一个数组包含 n+1 个成员，这些成员是 1 到 n 之间的整数。只有一个成员出现了两次，其他成员都只出现一次，请找出重复出现的那个数字。
============================================
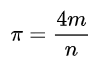
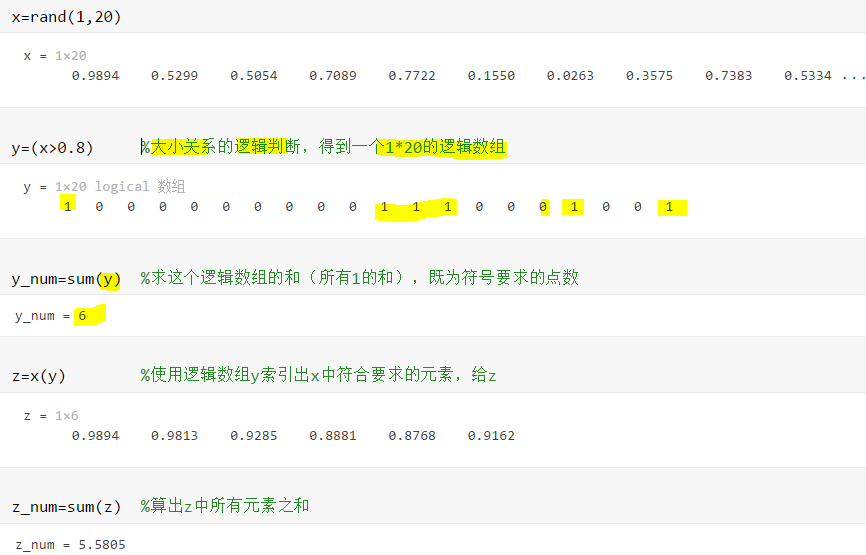
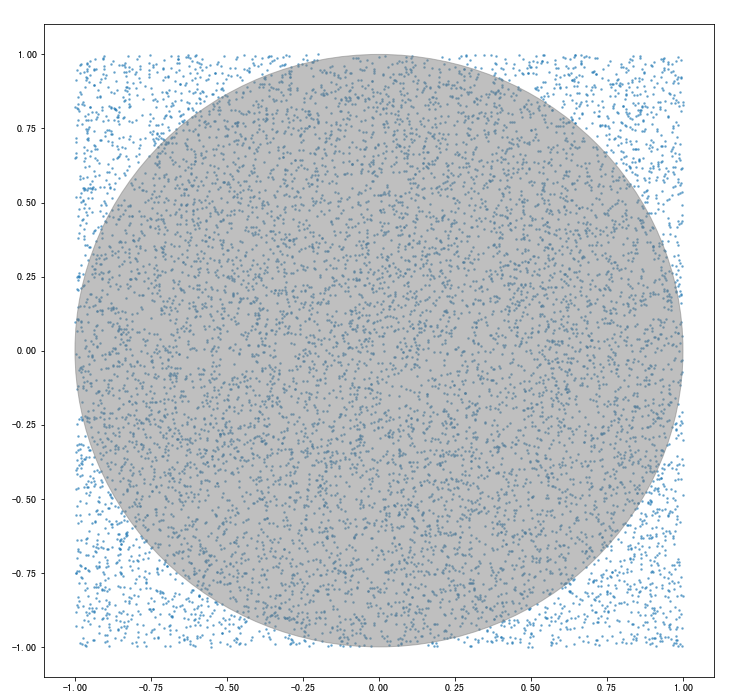
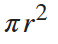
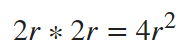
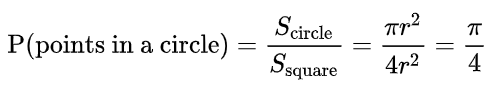
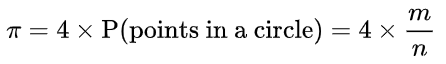
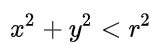来判别。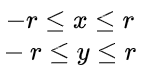
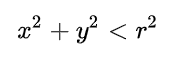则在圆内，否则在圆外。
