简单数学函数图像绘制：

1，欧拉公式的几何意义

欧拉公式（可以用泰勒展开证明），

显然，这表示复平面矢量，并且幅值是1，因为  ，而相角，  。

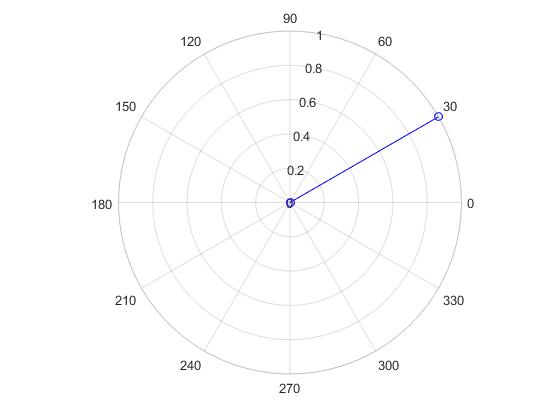
fig = figure(1);
i = sqrt(-1);    %确认i是-1
v1 = polarplot([0,exp(i*pi/6)],'bo-'); % 画上原点的目的是显示矢量

2，i和  的关系

通常意义上，  ，而  。

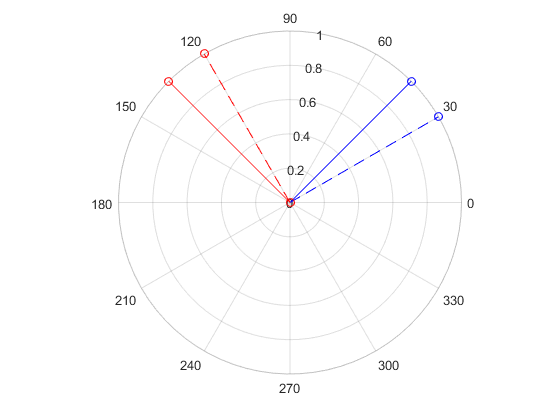
乘以i后，相位超前了  ，也就是90度。

figure(2);
% i 的作用
i = sqrt(-1);
v2 = polarplot([0,exp(i*pi/4)],'bo-');
hold on;
v3 = polarplot([0,i*exp(i*pi/4)],'ro-');

% pi/2的转角
v4 = polarplot([0,exp(i*pi/6)],'bo--');
v5 = polarplot([0,exp(i*(pi/6+pi/2))],'ro--');

3，  的意义

实数部分代表复平面矢量的幅值  ，而虚数部分在1中已经明确，即代表相位。

4， 的意义

通过1来推理，  ，这不显然单位长度旋转矢量？

figure(3)
i = sqrt(-1);
t = [0:0.01:10];
w = 2;
a = exp(i*w*t);
comet3(t,imag(a),real(a));

运行一下。

5，叠加出实信号 

在前一篇中聊到  为单位旋转矢量。这其中有一个隐藏条件就是，这是复平面内单位旋转矢量。那我们常见的信号可都是实信号啊，这需要一个叠加过程。这里可以很容易的推理出

fig = figure(1);
i = sqrt(-1);
w = 1;
t = [0:0.01:pi/6];    % 故意让wt不到2pi来更清晰表达转向。
v1 = exp(i*w*t);      % 正向转向的矢量，ccw
v2 = exp(-i*w*t);     % 逆向转向的矢量，cw

polarplot(v1,'r-');
hold on
polarplot(v2,'b--');    % cw
polarplot([0,v1(end)],'ro-');
polarplot([0,v2(end)],'bo--');
polarplot([real(v1(end)),v1(end)],'ro-');
polarplot([real(v2(end)),v2(end)],'bo--');
polarplot([0,real(v1(end))+real(v2(end))],'ko--');

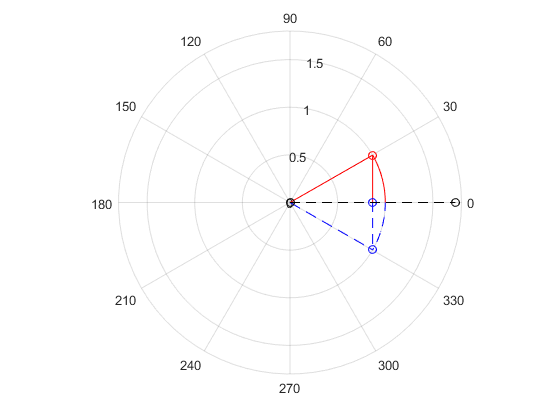
蓝色的线说明  是反向转的。利用奇偶性，易得：

复信号更具有一般性，而实信号只是一个复信号的子集。

在叠加复信号的过程会发现，同一正负频率的信号的幅值一定是相等的，这也是实信号傅立叶变换里为什么会有对称的结果。同时，也应该比较容易理解负频率的几何意义了吧？

6，  的实数部分

因为常见系统里都是实信号，先只研究下其实数部分。

这里需要说明的是，a为常实数。

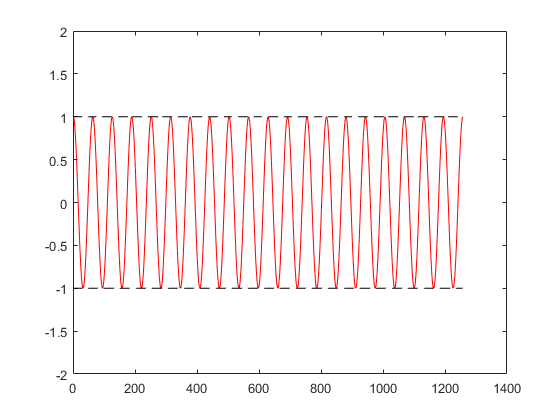
a = 0时，

fig = figure(2);
i = sqrt(-1);
w = 10;
t = [0:0.01:4*pi];   
v3 = exp(i*w*t);      % 正向转向的矢量，ccw
plot(real(v3),'r-');
hold on
plot(exp(0*t),'k--'); % 轮廓线
plot(-exp(0*t),'k--');
ylim([-2,2]);

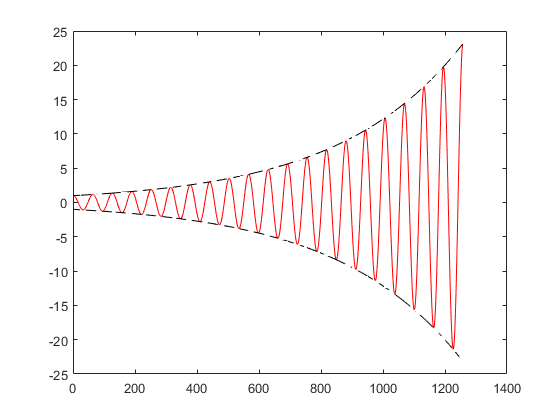
a > 0，取a=0.25，

fig = figure(3);
i = sqrt(-1);
w = 10;
t = [0:0.01:4*pi];
v4 = exp((0.25+i*w)*t);
plot(real(v4),'r-');
hold on
plot(exp(0.25*t),'k--'); % 轮廓线
plot(-exp(0.25*t),'k--');

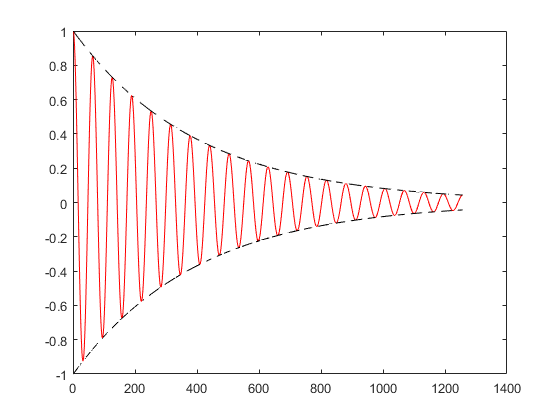
a < 0，取a=-0.25

fig = figure(4);
i = sqrt(-1);
w = 10;
t = [0:0.01:4*pi];
v4 = exp((-0.25+i*w)*t);
plot(real(v4),'r-');
hold on
plot(exp(-0.25*t),'k--'); % 轮廓线
plot(-exp(-0.25*t),'k--');