三维绘图

一．绘制三维曲线的基本函数

最基本的三维图形函数为plot3，它将二维绘图函数plot的有关功能扩展到三维空间，可以用来绘制三维曲线。其调用格式为：

plot3（x1，y1，z1，选项1，x2，y2，z2，选项2，…）

其中每一组x，y，z组成一组曲线的坐标参数，选项的定义和plot的选项一样。当x，y，z是同维向量时，则x，y，z对应元素构成一条三维曲线。当x，y，z是同维矩阵时，则以x，y，z对应列元素绘制三维曲线，曲线条数等于矩阵的列数。

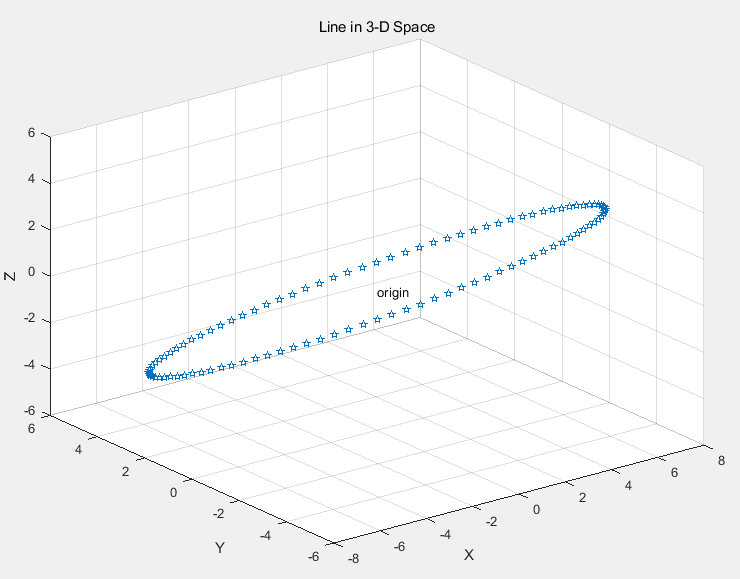
例 绘制空间曲线

该曲线对应的参数方程为

t=0:pi/50:2*pi;
x=8*cos(t);
y=4*sqrt(2)*sin(t);
z=-4*sqrt(2)*sin(t);
plot3(x,y,z,'p');
title('Line in 3-D Space');
text(0,0,0,'origin');
xlabel('X');
ylabel('Y');
zlabel('Z');
grid on;

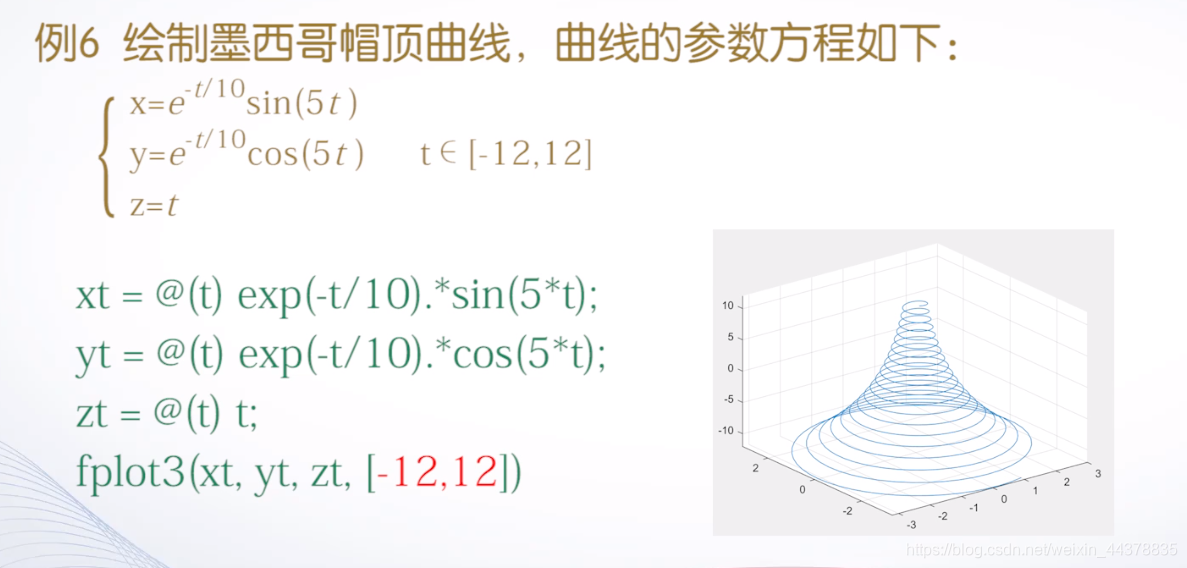
fplot3函数

例子：

二．三维曲面

1．平面网格坐标矩阵的生成

当绘制z=f(x,y)所代表的三维曲面图时，先要在xy平面选定一矩形区域，假定矩形区域为D＝[a,b]×[c,d]，然后将[a,b]在x方向分成m份，将[c,d]在y方向分成n份，由各划分点做平行轴的直线，把区域D分成m×n个小矩形。生成代表每一个小矩形顶点坐标的平面网格坐标矩阵，最后利用有关函数绘图。

产生平面区域内的网格坐标矩阵有两种方法：

方法1：利用矩阵运算生成。

x=a:dx:b;
y=(c:dy:d)’;
X=ones(size(y))*x;
Y=y*ones(size(x));

%或者用repmat函数。
x=0:1:9 ;                         %1行10列
y=[10:0.1:11.9]' ;             %1行20列
X=repmat(x , size(y,1) , 1)   % size(y,1)的到y的行数
Y=repmat(y , 1 , size(x,2))   % size(x,2)的到x的列数

经过上述语句执行后，矩阵X的每一行都是向量x，行数等于向量y的元素个数，矩阵Y的每一列都是向量y，列数等于向量x的元素个数。

方法2：利用meshgrid函数生成；

1. meshgrid
1.1 作用
meshgrid 函数用于生成二维或三维网络坐标。
1.2 语法
[X,Y] = meshgrid(x,y)
[X,Y] = meshgrid(x)
[X,Y,Z] = meshgrid(x,y,z)
[X,Y,Z] = meshgrid(x)

[X,Y] = meshgrid(x,y)
基于 x、y 坐标向量返回二维网络点对应的坐标矩阵。X、Y 为网络点对应维度的坐标矩阵，
其中 X 每一行为 x 的一个副本，Y 每一列为 y 的一个副本。且 size(X) = size(Y) = [length(y),length(x)] 。

[X,Y] = meshgrid(x)
该语法等价于 [X,Y] = meshgrid(x,x)，由上述语法可知，该语法返回网格大小为 length(x)length(x) 的方形网格坐标。

[X,Y,Z] = meshgrid(x,y,z)
基于 x、y、z 坐标向量返回三维网络点对应的坐标矩阵。X、Y、Z 为网络点对应维度的坐标矩阵，
其中 X 沿第二维度（行）均为 x 的副本，Y 沿第一维度（列）均为 y 的副本，Z 沿第三维度均为 z 的副本。
且 size(X) = size(Y) = size(Z) = [length(y),length(x),length(z)] 。

[X,Y,Z] = meshgrid(x)
该语法等价于 [X,Y,Z] = meshgrid(x,x,x)，由上述语法可知，
该语法返回网格大小为 length(x)length(x)length(x) 的三维网格坐标。

链接：https://www.jianshu.com/p/6200693ed339


例：
x=1:4;
y=5:7;
[X,Y]=meshgrid(x,y)

当x=y时，可以写成meshgrid(x)

meshgrid还可以用于替代循环，优化程序效率，如下：

x = 1:5000;
y = 5001:10000;
z = zeros(5000);
ans0 = zeros(5000,5000);

tic
for i = 1:5000
    for j = 1:5000
    ans0(i,j) = x(i)^2 + y(j)^2;
    end
end
toc                                            %0.491108s



tic
[X,Y] = meshgrid(x,y);
ans1 = X.^2 + Y.^2;
toc                                            %0.187623s

2．绘制三维曲面的函数

Matlab提供了mesh函数和surf函数来绘制三维曲面图。mesh函数用来绘制三维网格图，而surf用来绘制三维曲面图，各线条之间的补面用颜色填充。其调用格式为：

mesh（x，y，z，c）

surf（x，y，z ，c）

一般情况下，x，y，z是维数相同的矩阵，x，y是网格坐标矩阵，z是网格点上的高度矩阵，c用于指定在不同高度下的颜色范围。c省略时，Matlab认为c=z，也即颜色的设定是正比于图形的高度的。这样就可以得到层次分明的三维图形。当x，y省略时，把z矩阵的列下标当作x轴的坐标，把z矩阵的行下标当作y轴的坐标，然后绘制三维图形。当x，y是向量时，要求x的长度必须等于z矩阵的列，y的长度必须等于必须等于z的行，x，y向量元素的组合构成网格点的x，y坐标，z坐标则取自z矩阵，然后绘制三维曲线。

例 用三维曲面图表现函数 ：

为了便于分析三维曲面的各种特征，下面画出3种不同形式的曲面。

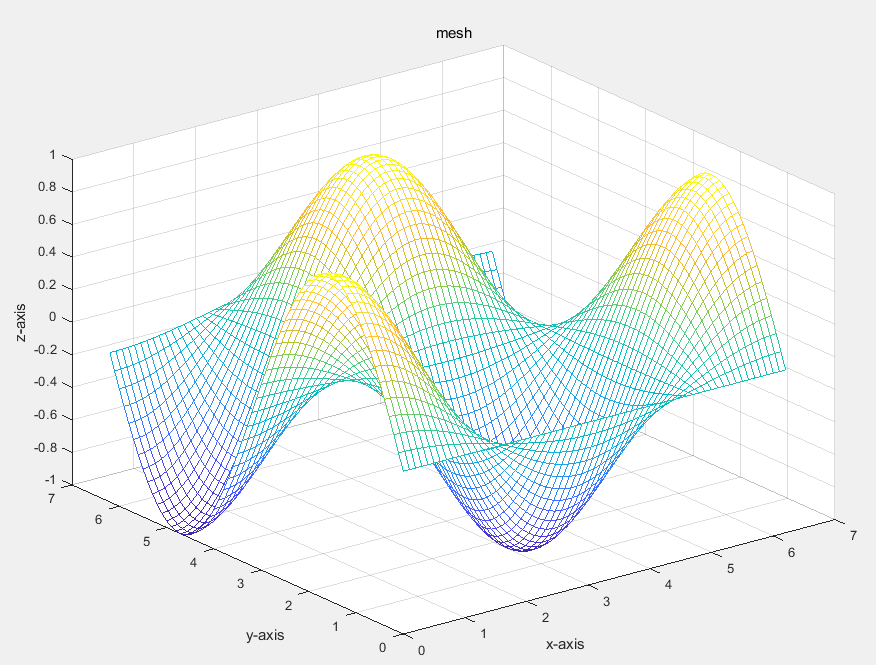
%program 1
x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
mesh(x,y,z);
xlabel('x-axis')；
ylabel('y-axis')；
zlabel('z-axis');
title('mesh');
grid on;

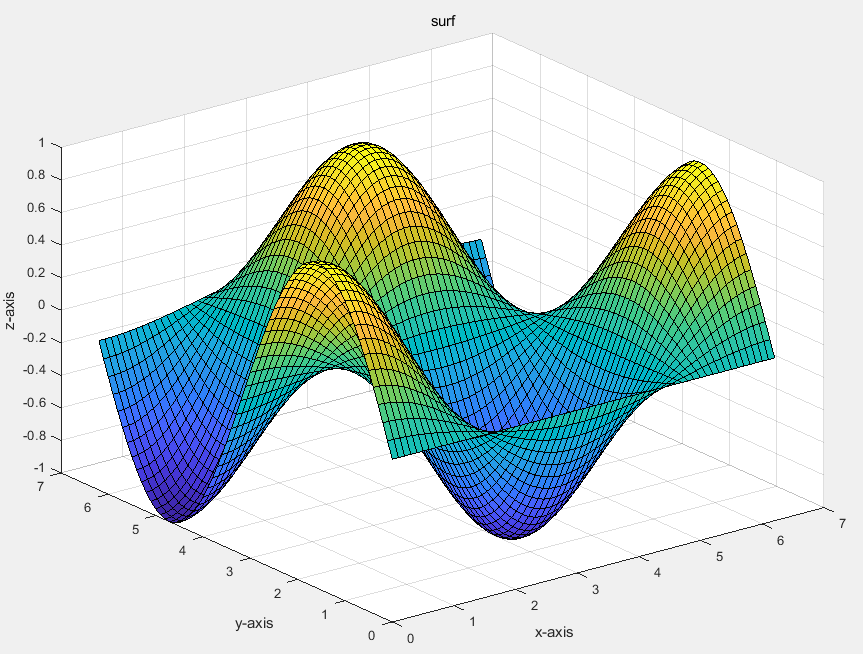
%program 2
x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
surf(x,y,z);
xlabel('x-axis')；
ylabel('y-axis')；
zlabel('z-axis');
title('surf');
grid;



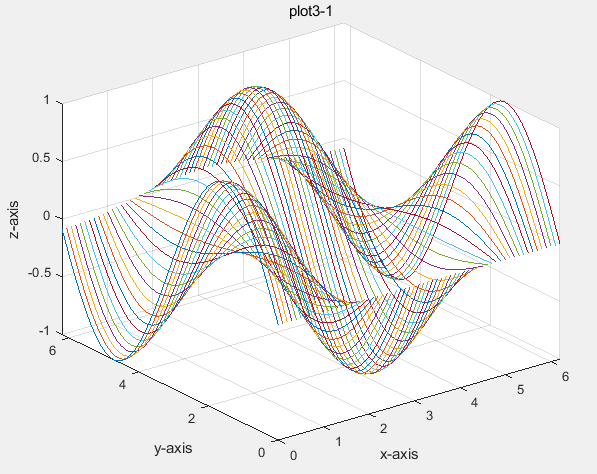
%program 3
x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
plot3(x,y,z);
xlabel('x-axis')；
ylabel('y-axis')；
zlabel('z-axis');
title('plot3-1');
grid;

网格图（mesh）中线条有颜色，线条间补面无颜色。曲面图（surf）的线条都是黑色的，线条间补面有颜色。进一步观察，曲面图补面颜色和网格图线条颜色都是沿z轴变化的。用plot3 绘制的三维曲面实际上由三维曲线组合而成。可以分析plot（x’，y’，z’）所绘制的曲面的特征。

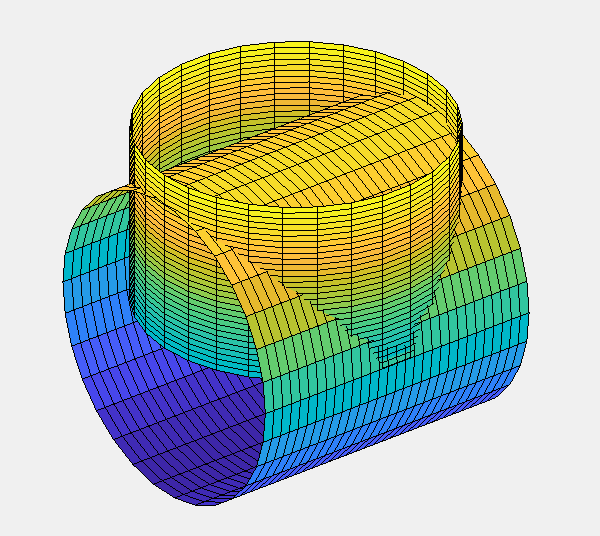
例 绘制两个直径相等的圆管相交的图形。

m=30;
z=1.2*(0:m)/m;
r=ones(size(z));
theta=(0:m)/m*2*pi;
x1=r'*cos(theta);y1=r'*sin(theta);%生成第一个圆管的坐标矩阵
z1=z'*ones(1,m+1);
x=(-m:2:m)/m;
x2=x'*ones(1,m+1);y2=r'*cos(theta);%生成第一个圆管的坐标矩阵
z2=r'*sin(theta);
surf(x1,y1,z1);         
%绘制竖立的圆管
axis equal 
axis off
hold on
surf(x2,y2,z2);         
%绘制平放的圆管
axis equal ,axis
off
title ('两个等直径圆管的交线');
hold off

例 分析由函数 构成的曲面形状与平面z=a的交线。

此外，还有两个和mesh函数相似的函数，即带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz，其用法和mesh类似。不同的是，meshc还在xy平面上绘制曲面在z轴方向的等高线，meshz还在xy平面上绘制曲面的底座。

surf函数也有两个类似的函数，即具有等高线的曲面函数surfc和具有光照效果的曲面函数surfl。

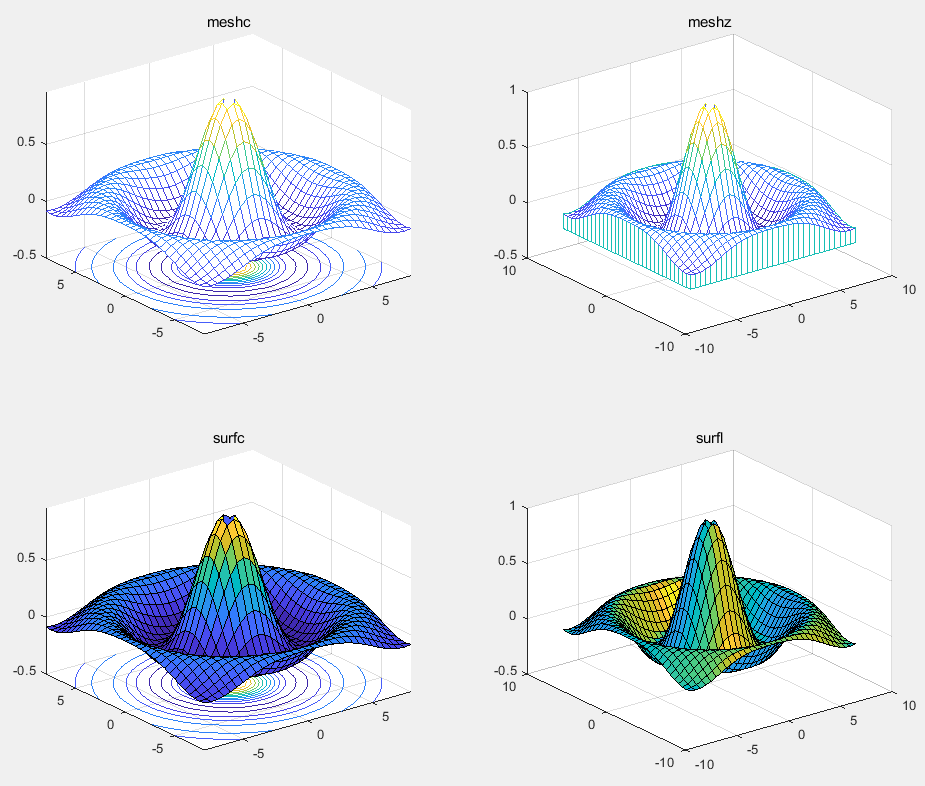
例 在xy平面内选择[-8, 8]×[－8, 8]绘制函数，

[x,y]=meshgrid(-8:0.5:8);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);
subplot(2,2,1);
meshc(x,y,z);
title('meshc');
subplot(2,2,2);
meshz(x,y,z);
title('meshz');
subplot(2,2,3);
surfc(x,y,z);
title('surfc');
subplot(2,2,4);
surfl(x,y,z);
title('surfl');

ezmesh('sin(x^2)+cos(y^2)-1',[-5 ,5] ,300)

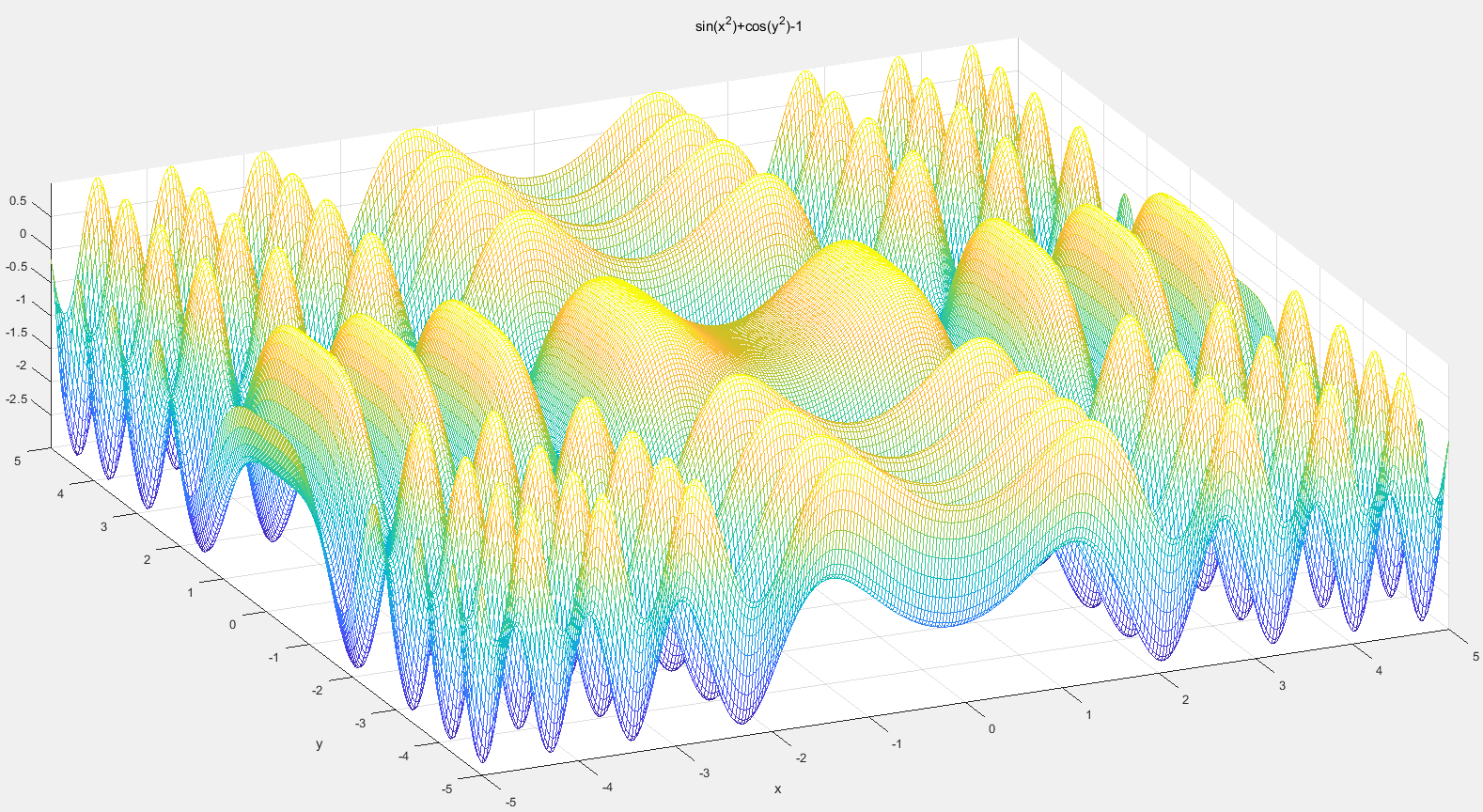
fsurf函数和fmesh函数

3．标准三维曲面

Matlab提供了一些函数用于绘制标准三维曲面，这些函数可以产生相应的绘图数据，常用于三维图形的演示。如，sphere函数和cylinder函数分别用于绘制三维球面和柱面。sphere函数的调用格式为：

[x,y,z]=sphere(n);

该函数将产生（n+1）×（n+1矩阵x，y，z 。采用这三个矩阵可以绘制出圆心位于原点、半径为1的单位球体。若在调用该函数时不带输出参数，则直接绘制所需球面。n决定了球面的圆滑程度，其默认值为20。若n值取的比较小，则绘制出多面体的表面图。

cylinder函数的调用格式为：

[x，y，z]＝cylinder（R，n）

其中R是一个向量，存放柱面各个等间隔高度上的半径，n表示在圆柱圆周上有n个间隔点，默认有20个间隔点。如：cylinder（3）生成一个圆柱，cylinder（[10，1]）生成一个圆锥。而t=0:pi/100:4*pi; R=sin(t); cylinder(R,30);生成一个正弦圆柱面。

另外Matlab还提供了一个peaks函数，称为多峰函数，常用于三维曲面的演示。该函数可以用来生成绘图数据矩阵，矩阵元素由函数：

在矩形区域[－3 3]×[－3 3]的等分网格点上的函数值确定。如：z=peaks（30）

将生成一个30×30矩阵，

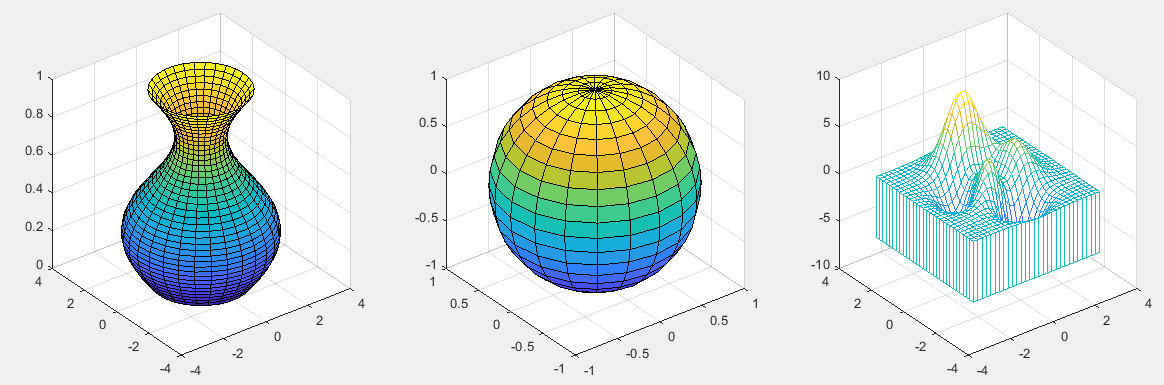
例 绘制标准三维曲面图形

t=0:pi/20:2*pi;
[x,y,z]=cylinder(2+sin(t),30);
subplot(1,3,1);
surf(x,y,z);
subplot(1,3,2);
[x,y,z]=sphere;
surf(x,y,z);
subplot(1,3,3);
[x,y,z]=peaks(30);
meshz(x,y,z);

3．其他三维图形。

在介绍二维图形时，曾经提到条形图、杆图、饼图和填充图等特殊图形，它们还可以以三维形式出现，其函数分别为bar3，stem3，pie3和fill3。

bar3绘制三维条形图，常用格式为：

bar3（y）；

bar3（x，y）

在第一种格式中，y的每个元素对应于一个条形。第二种格式在x指定的位置上绘制y中元素的条形图。

stem3函数绘制离散序列数据的三维杆图，常用格式为：

stem3（z）

stem3（x，y，z）

第一种格式将数据序列z表示为从xy平面向上延伸的杆图，x和y自动生成。第二种格式在x和y指定的位置上绘制数据序列z的杆图，x，y，z的维数要相同。

pie3函数绘制三维饼图，常用格式为：

pie3（x）

x为向量，用x中的数据绘制一个三维饼图。

fill3函数可在三维空间内绘制出填充过的多边形，常用格式为：

fill3（x，y，z，c）

用x，y，z做多边形的顶点，而c指定了填充的颜色。

例 绘制三维图形。

1绘制魔方阵的三维条形图

2以三维杆图形式绘制曲线y=2sinx

3已知x ＝[2347,1827,2043,3025] ，绘制三维饼图

4用随机的顶点坐标值画出5个黄色三角形

subplot(2,2,1);
bar3(magic(4));
subplot(2,2,2);
y=2*sin(0:pi/10:2*pi);
stem3(y);
subplot(2,2,3);
pie3([2347,1827,2043,3025]);
subplot(2,2,4);
fill3(rand(3,5),rand(3,5),rand(3,5),'y');

除了上面讨论的三维图形外，常用的图形还有瀑布图和三维曲面的等高线图。绘制瀑布图用waterfall函数，用法和meshz函数相似，只是它的网格线在x轴方向出现，具有瀑布效果。等高线图分二维和三维两种形式，分别使用函数contour和contour3绘制。

例 绘制多峰函数的瀑布图和等高线图。

subplot(1,2,1);
[X,Y,Z]=peaks(30);
waterfall(X,Y,Z);
xlabel('XX');ylabel('YY');zlabel('ZZ');
subplot(1,2,2);
contour3(X,Y,Z,12,'k');%其中12代表高度的等级数
xlabel('XX');ylabel('YY');zlabel('ZZ');

三．三维图形的精细处理

1．视点处理

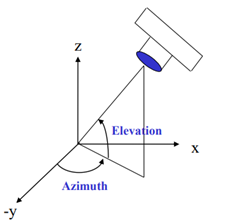
在日常生活中，从不同的角度观察物体，所看到的物体形状是不一样的。同样，从不同视点绘制的三维图形的形状也是不一样的。视点位置可由方位角和仰角表示。

方位角

Matlab提供了设置视点的函数view，其调用格式为：

view（az，el）

其中az为方位角，el为仰角，它们均以度为单位。系统默认的视点定义为方位角为-37.5度，仰角30度。

例 从不同视点绘制多峰函数曲面。

subplot(2,2,1);mesh(peaks);
view(-37.5,30);
title('1');
subplot(2,2,2);mesh(peaks);
view(0,90);
title('2');
subplot(2,2,3);mesh(peaks);
view(90,0);
title('3');
subplot(2,2,4);mesh(peaks);
view(-7,-10);
title('4');

2．色彩处理

3．图形的裁剪处理

Matlab定义的NaN常数可以用于表示那些不可使用的数据，利用这些特性，可以将图形中需要裁剪部分对应的函数值设置成NaN，这样在绘制图形时，函数值为NaN的部分将不显示出来，从而达到对图形进行裁剪的目的。例如，要削掉正弦波顶部或底部大于0.5的部分，可使用下面的程序。

x=0:pi/10:4*pi;
y=sin(x);
i=find(abs(y)>0.5);
x(i)=NaN;
plot(x,y);

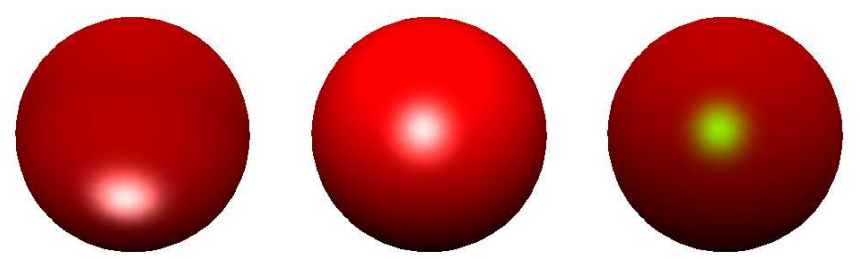
例 绘制两个球面，其中一个在另一个里面，将外面的球裁掉一部分，以便能看到里面的球。

[x,y,z]=sphere(25);
%生成外面的大球
z1=z;
z1(:,1:4)=NaN;%将大球裁去一部分
c1=ones(size(z1));
surf(3*x,3*y,3*z1,c1);
      %生成里面的小球
hold on
z2=z;
c2=2*ones(size(z2));
c2(:,1:4)=3*ones(size(c2(:,1:4)));
surf(1.5*x,1.5*y,1.5*z2,c2);
colormap([0 1
0;0.5 0 0;1 0 0]);
grid on
hold off

色图中使用三种颜色，外面的球是绿色，里面的球采用深浅不同的两种红色。

===================================================

以下为具体实例：

绘制三维螺旋曲线

1 t=0:pi/50:10*pi;
2 x=sin(t),y=cos(t);
3 plot3(x,y,t);
4 title('helix'),text(0,0,0,'origin');
5 xlabel('sin(t)'),ylabel('cos(t)'),zlabel('t');
6 grid on;%加上虚线网格线可以更好的看到对应区间的值

九.绘制三维网格图。函数格式：mesh(x,y,z,c)
其中：x，y控制X和Y轴坐标
       矩阵z是由(x，y)求得Z轴坐标
       (x,y,z)组成三维空间的网格点
       c用于控制网格点颜色

1 %绘制三维网格曲面图
2 x=[0:0.15:2*pi];
3 y=[0:0.15:2*pi];
4 z=sin(y')*cos(x); %矩阵相乘
5 mesh(x,y,z);

1 %画出由函数形成的立体网状图：
2 x=linspace(-2, 2, 25); % 在x轴上取25点 
3 y=linspace(-2, 2, 25); % 在y轴上取25点 
4 [xx,yy]=meshgrid(x,y); % xx和yy都是21x21的矩阵 
5 zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值，zz也是21x21的矩阵 
6 mesh(xx, yy, zz); % 画出立体网状图

十.surf函数

绘制三维曲面图，各线条之间的补面用颜色填充。surf函数和mesh函数的调用格式一致。
函数格式: surf (x,y,z)
其中x，y控制X和Y轴坐标，矩阵z是由x，y求得的曲面上Z轴坐标。

1 % 绘制三维曲面图
2 x=[0:0.15:2*pi];
3 y=[0:0.15:2*pi];
4 z=sin(y')*cos(x); %矩阵相乘
5 surf(x,y,z);

1 %剔透玲珑球
2 [X0,Y0,Z0]=sphere(30);       %产生单位球面的三维坐标
3 X=2*X0;Y=2*Y0;Z=2*Z0;     %产生半径为2的球面的三维坐标,若加上常数则是圆心
4 surf(X0,Y0,Z0);          %画单位球面
5 shading interp               %采用插补明暗处理
6 hold on; mesh(X,Y,Z);hold off       %画外球面
7 hidden off                    %产生透视效果
8 axis off          %不显示坐标轴

 1 %卫星返回地球的运动轨线示意。
 2 R0=1;            %以地球半径为一个单位
 3 a=12*R0;b=9*R0;T0=2*pi;       %T0是轨道周期
 4 T=5*T0;dt=pi/100;t=[0:dt:T]';f=sqrt(a^2-b^2);  %地球与另一焦点的距离
 5 th=12.5*pi/180;    %卫星轨道与x-y平面的倾角
 6 E=exp(-t/20);    %轨道收缩率
 7 x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t));
 8 plot3(x,y,z,'g')    %画全程轨线
 9 [X,Y,Z]=sphere(30);X=R0*X;Y=R0*Y;Z=R0*Z;  %获得单位球坐标
10 grid on,hold on,surf(X,Y,Z),shading interp     %画地球
11 x1=-18*R0;x2=6*R0;y1=-12*R0;y2=12*R0;z1=-6*R0;z2=6*R0;
12 axis([x1 x2 y1 y2 z1 z2])    %确定坐标范围
13 view([117 37]),comet3(x,y,z,0.02),hold off     %设视角、画运动轨线

十一.等高线图

1 %多峰函数peaks的等高线图
2 [x,y,z]=peaks(30);%产生一个凹凸有致的曲面，包含了三个局部极大点及三个局部极小点
3 contour3(x,y,z,16);
4 xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');
5 title('contour3 of peaks')

十二. 动画设计

1 %动画功能函数：getframe、moviein和movie
2 %播放一个不断变化的眼球程序。
3 m=moviein(20); %建立一个20个列向量组成的矩阵
4 for j=1:20
5    plot(fft(eye(j+10))) %绘制出每一幅眼球图并保存到m矩阵中
6    m(:,j)=getframe;
7 end
8 movie(m,10);%以每秒10幅的速度播放画面

三维图的视角与打光

调整视角

使用view()函数可以调整视角,view()函数接受两个浮点型参数,分别表示两个方位角azimuth
和elevation.

sphere(50); shading flat;
material shiny;
axis vis3d off;
view(-45,20);

调整打光

使用light()函数可以对三维图形进行打光,并返回光源的句柄.

[X, Y, Z] = sphere(64); h = surf(X, Y, Z);
axis square vis3d off;
reds = zeros(256, 3); reds(:, 1) = (0:256.-1)/255;
colormap(reds); shading interp; lighting phong;
set(h, 'AmbientStrength', 0.75, 'DiffuseStrength', 0.5);
L1 = light('Position', [-1, -1, -1])

通过对光源的句柄进行操作可以修改光源的属性

set(L1, 'Position', [-1, -1, 1]);
set(L1, 'Color', 'g');

light()用于打光；

patch()用于画多边形；

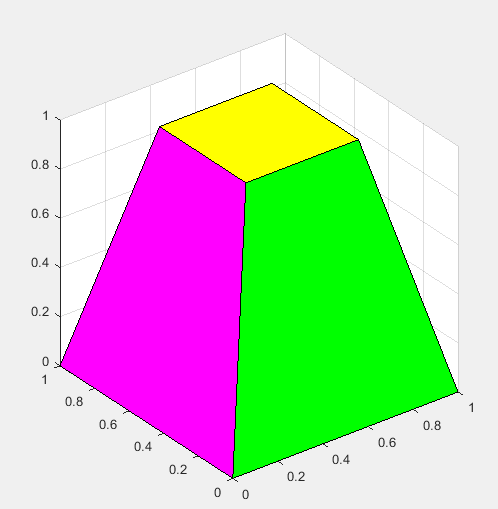
v=[0 0 0;1 0 0;1 1 0;0 1 0;...               %这里分别指的是8个顶点里下面4个顶点的坐标；

    0.25 0.25 1;0.75 0.25 1;0.75 0.75 1;0.25 0.75 1];   %这里分别指的是8个顶点里上面4个顶点的坐标；

f=[1 2 3 4;     %这里指的是面的连接，将第1个顶点与第2个相连，2与3连，3与4连，下面相同

    5 6 7 8;

    1 2 6 5;

    2 3 7 6;

    3 4 8 7;

    4 1 5 8];

subplot(1,2,1);

patch('Vertices',v,...      %顶点坐标

    'Faces',f,...           %定义每个面的顶点连接

    'FaceVertexCData',hsv(6),...    %属性是面和顶点颜色，hsv(m) 是产生包含m 个颜色的颜色图

    'FaceColor','flat');      %面颜色，对于插值颜色，请将此属性指定为 'interp'。对于统一颜色，请将此属性指定为 'flat'。

view(3);    axis square tight; grid on;

=======================================================

matlab中如何将多张图片堆叠起来呢？

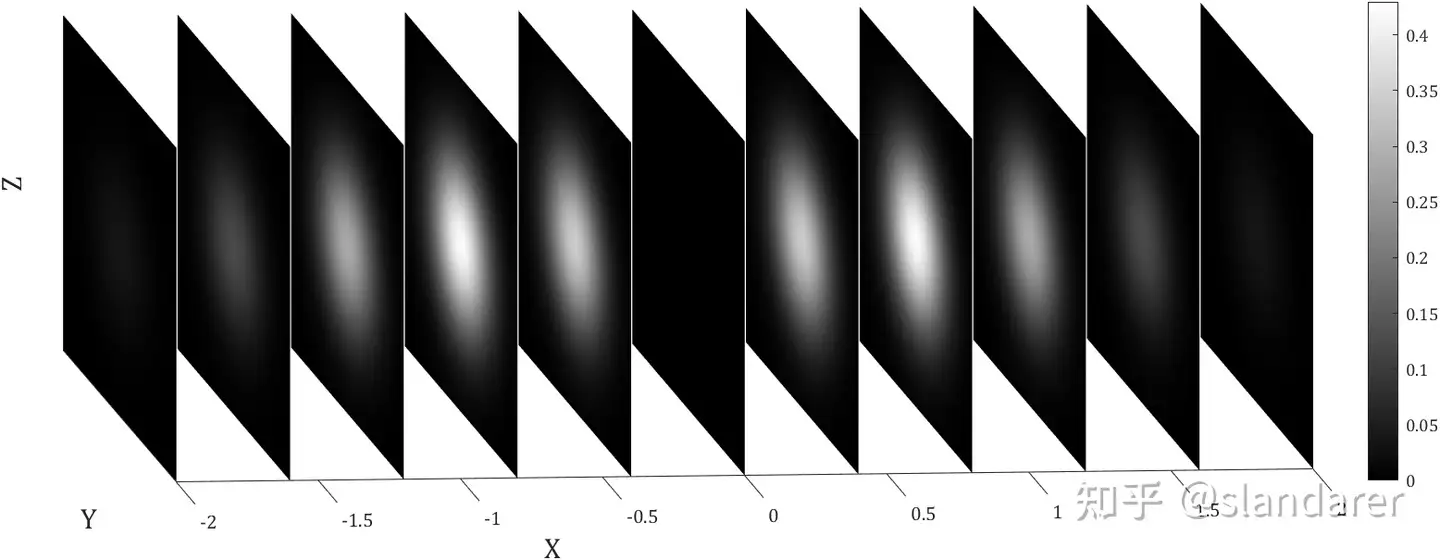
[X,Y,Z]=meshgrid(-2:.02:2);
V=abs(X.*exp(-X.^2-Y.^2-Z.^2));


fig=figure('Position',[100,300,1200,420]);
ax=gca;hold on;view(-5.6541,21.6597)
xslice=-2:.4:2;  
sliceHdl=slice(X,Y,Z,V,xslice,[],[]);
for i=1:length(sliceHdl)
    set(sliceHdl(i),'EdgeColor','none')
end
colormap(gray)
colorbar

% 坐标区域修饰
ax.FontName='Cambria';
ax.XLabel.String='X';
ax.YLabel.String='Y';
ax.ZLabel.String='Z';
ax.XLabel.FontSize=15;
ax.YLabel.FontSize=15;
ax.ZLabel.FontSize=15;
ax.YTick=[];
ax.ZTick=[];

用surf(X,Y,Z,C)来做，多画几次，每次Z为固定值，C为颜色，画完以后旋转坐标系。因为matlab好像不太好按Z轴旋转，所以把Y和Z轴的数据互换了一下。clc,clear

x = [-1:0.05:1]';

y = [-1:0.05:1]';

z = [-10:2:10]';

[X,Y] = meshgrid(x,y);

hold on

for i = 1 : length(z)

    Z = z(i)*ones(size(X));

C = X.^2.*Y.^2*z(i);

surf(X,Z,Y,C)%注意顺序

end

shading flat

xlabel("X");

zlabel("Y");

ylabel("Z");

xlim([-1 1]);

zlim([-1 1]);

ylim([-10 10]);

colorbar;

view(85,20);

set(gcf,'unit','normalized','position',[0.03 0.03 0.8 0.4]);