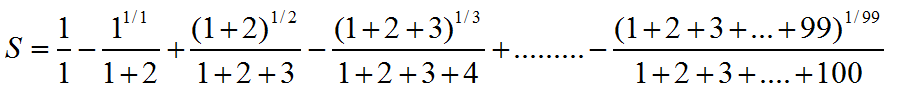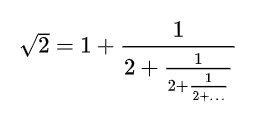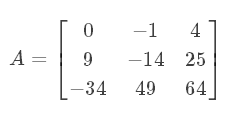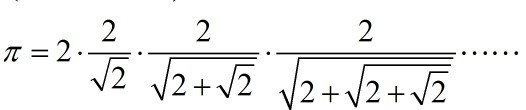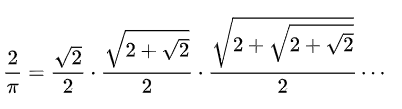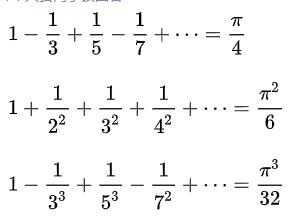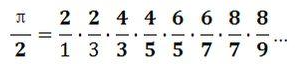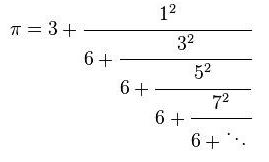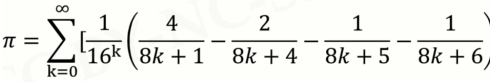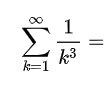for循环
for循环是一种重复控制结构,可以让您有效地编写一个需要执行特定次数的循环。
1. for循环的基本语法
for 循环控制变量=start:step:end %有序数组模式
语句
end
==============================================
或:
for 循环控制变量=数组表达式 %无序数组模式
语句
end
以上两种表达式可以抽象为如下语句:
for index = values
<program statements>
...
end
值(values)具有以下格式 -
| 值格式 | 描述 |
|---|
| initval:endval | index变量从initval到endval每次递增1,并重复程序语句的执行,直到index大于endval。 |
| initval:step:endval | 通过每次迭代值步长(step)增加索引(index)的值,或者当step为负时递减。 |
| valArray | 在每个迭代中从数组valArray的后续列创建列向量索引。 例如,在第一次迭代中,index = valArray(:,1)。 循环最多执行n次,其中n是由numel(valArray,1,:)给出的valArray的列数。valArray可以是任何MATLAB数据类型,包括字符串,单元格数组或结构体。 |
initval:step:endval 模式
例 :
for a = 0:2:10
y= a^2 ;
fprintf(' 循环变量a 的当前值 平方后为: %d \n', y);
end

例 :
for a = 1: -0.1: 0
disp(a)
end
运行示例代码时,会显示以下结果 -
1
0.90000
0.80000
0.70000
0.60000
0.50000
0.40000
0.30000
0.20000
0.10000
0
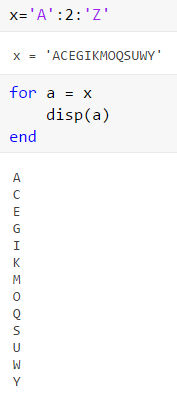
valArray模式 (无序数组模式)
例子:
for a = [24,18,17,-3,28] %循环控制变量=数组表达式
disp(a)
end
运行示例代码时,会显示以下结果 -
24
18
17
-3
28
上述代码可以改为 initval:step:endval 模式,如下
x=[24,18,17,-3,28]
for k= 1:5 %此时循环变量k 充当数组x的下标
disp( x(k) )
end

例:
A = rand(3,4)
%如果A是一个矩阵,for循环会按列的进行循环,并且循环变量每次取A(:,i)
for a = A
a % 相当于A(:,i)
end
运行结果:

for循环课堂练习:
1)求和:s=1+2+3+......+100
s = 0;
for n = 1:100
s = s + n;
end
s
和while循环的对比:
s=0;
k=1;
while k<101
s=s+k;
k=k+1;
end
s
向量化编程:
x=1:100;
s=sum(x)
2)求和:S=1*2*3+2*3*4+………+50*51*52
s = 0;
for k= 1:50
s = s + k*(k+1)*(k+2) ;
end
s
和while循环的对比:
s=0;
k=1;
while k<=50
s=s+k*(k+1)*(k+2);
k=k+1;
end
s
向量化编程:
x1=1:50;
x2=2:51;
x3=3:52;
x=x1.*x2.*x3;
s=sum(x)
3)数组x=randn(1,20),求数组中所有元素平方和。
%方法1
x=randn(1,20);
s=0;
for n=x %无序数组模式
s=s+n^2;
end
s
%方法2
x=randn(1,20);
L=length(x);
for k=1:L %有序数组模式
s=s+x(k)^2;
end
s
%方法3 %向量化思维
x=randn(1,20);
s=sum(x.^2)
如果题目改为,求数组中偶数位置的元素的平方和,以上3种程序该怎么写?
%方法1
x=randn(1,20);
s=0;
L=length(x);
for k=2:2:L %有序数组模式
s=s+x(k)^2;
end
s
%方法2
x=randn(1,20);
s=0;
k=1; %k用来记录当前循环的次数。
for n=x %无序数组模式
if mod(k,2)==0
s=s+n^2;
end
k=k+1;
end
s
%方法3 %向量化思维
x=randn(1,20);
s=sum( x( [2:2:20] ).^2 )
4)利用蒙特卡洛法计算圆周率
n=10000; %n为总点数
m=0; %m为落于半径为1的圆内的点数
for i=1:n
x=rand(1); %生成第i个点的x,y坐标
y=rand(1);
if x^2+y^2<=1 %判断第i个点在不在圆内
m=m+1; %在圆内的话,计数器m加1
end
end
mypai=4*m/n
5)编程生成斐波那契数列前20项
斐波拉契数列是指这样的一组数列 1、1、2、3、5、8、13、21……
这个数列的规律是:从第三项开始每一项值都等于前两项之和: F(n)=F(n-1)+F(n-2)
斐波那契数列又称黄金分割数列,因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)
以兔子繁殖为例子而引入,故又称为“兔子数列”。
在数学上,斐波纳契数列以如下被以递归的方法定义:
F(1)=1 ,
F(2)=1 ,
F(n)=F(n-1)+F(n-2) (n>=3,n∈N*)
% 计算斐波那契数列前M项
M=20;
F = zeros(1, M); % 用数组F来记录前M项,每一项都初始化为0
F(1) = 1; %第1项需要手动赋值为1
F(2) = 1; %第2项需要手动赋值为1
for n = 3:M %从第3项开始,当前项等于前面两项之和。
F(n) = F(n-1) + F(n-2);
end
F
%如果想一行显示5个数,上述程序该怎么改?
M=30;
F = zeros(1, M); % 用数组F来记录前M项,每一项都初始化为0
F(1) = 1; %第1项需要手动赋值为1
F(2) = 1; %第2项需要手动赋值为1
for n = 3:M %从第3项开始,当前项等于前面两项之和。
F(n) = F(n-1) + F(n-2);
end
%下述操作可以实现一行显示5个数后换行。。。
for k = 1:M %用k表示数组F的下标
fprintf('%8d ',F(k))
if rem(k,5)==0 %如果k是5的倍数,则换行
fprintf('\n ')
end
end
练习:验证魔方矩阵的主、副对角线元素之和相等。
x=magic(11);
n=length(x);
sum_L=0;
sum_R=0;
for k=1:n
sum_L=sum_L+x(k,k);
sum_R=sum_R+x(k,n+1-k);
end
sum_L
sum_R
MATLAB允许在一个循环中使用另一个循环,即嵌套循环。
for循环的嵌套:
for i= 1:N
for j = 1:M
<statements>;
end
end
while循环的嵌套:
while <expression1>
while <expression2>
<statements>
end
end
例 - 4 使用嵌套的for循环来制作99乘法表。
for n=1:9
for m=1:9
fprintf( '%d * %d =%d ',n,m,n*m)
end
fprintf('\n ')
end
执行以上示例代码,得到以下结果 -
1 * 1 = 1 1 * 2 = 2 1 * 3 = 3 1 * 4 = 4 1 * 5 = 5 1 * 6 = 6 1 * 7 = 7 1 * 8 = 8 1 * 9 = 9
2 * 1 = 2 2 * 2 = 4 2 * 3 = 6 2 * 4 = 8 2 * 5 =10 2 * 6 =12 2 * 7 =14 2 * 8 =16 2 * 9 =18
3 * 1 = 3 3 * 2 = 6 3 * 3 = 9 3 * 4 =12 3 * 5 =15 3 * 6 =18 3 * 7 =21 3 * 8 =24 3 * 9 =27
4 * 1 = 4 4 * 2 = 8 4 * 3 =12 4 * 4 =16 4 * 5 =20 4 * 6 =24 4 * 7 =28 4 * 8 =32 4 * 9 =36
5 * 1 = 5 5 * 2 =10 5 * 3 =15 5 * 4 =20 5 * 5 =25 5 * 6 =30 5 * 7 =35 5 * 8 =40 5 * 9 =45
6 * 1 = 6 6 * 2 =12 6 * 3 =18 6 * 4 =24 6 * 5 =30 6 * 6 =36 6 * 7 =42 6 * 8 =48 6 * 9 =54
7 * 1 = 7 7 * 2 =14 7 * 3 =21 7 * 4 =28 7 * 5 =35 7 * 6 =42 7 * 7 =49 7 * 8 =56 7 * 9 =63
8 * 1 = 8 8 * 2 =16 8 * 3 =24 8 * 4 =32 8 * 5 =40 8 * 6 =48 8 * 7 =56 8 * 8 =64 8 * 9 =72
9 * 1 = 9 9 * 2 =18 9 * 3 =27 9 * 4 =36 9 * 5 =45 9 * 6 =54 9 * 7 =63 9 * 8 =72 9 * 9 =81
思考:如何制作如下的乘法口诀表
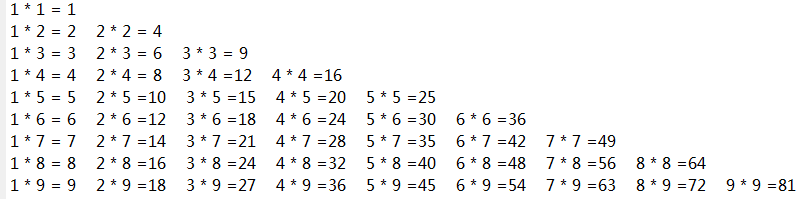
课题练习1:使用嵌套For循环创建一个10*10的希尔伯特矩阵


例 - 5 编程计算矩阵A中下标之和能被3整除的所有元素之和。
A=randi([-10,40],[5,9])
[N M]=size(A); %通过size()函数测量得到矩阵A的行号和列号,分别给N和M
s=0;
for n=1:N %n表示行号
for m=1:M %m表示列号
if mod( (n+m) , 3 )==0 %如果行号与列号之和可以被3整除
s=s+A(n,m);
end
end
end
s
运行上述代码:
A =
-9 21 -1 -2 -7 -6 23 13 -2
27 21 2 39 24 31 16 12 9
15 33 35 26 -8 31 39 32 32
14 31 -9 15 -7 26 23 -6 30
36 19 14 14 16 -3 30 -4 -7
s =
305
拓展练习:如果A是一个三维立体矩阵,如A=randi([-10,40],[5,9,3]),上述代码该如何修改?
例:设数组为x=[1:55],编写程序,使得数组按照第一行输出1个,第二行输出2个....第10行输入10个元素的方式输出该数组。效果如下:
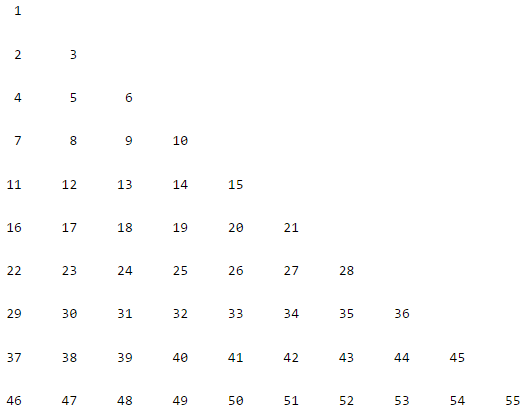
方法1:双重for循环
clear
x=1:55;
k=1; %k表示数组x的元素的索引号,初始化为1
for n=1:10 %表示依次遍历1-10行
for m=1 : n %表示每一行依次从1数到n
fprintf('%4d ',x(k))
k=k+1; %k+1,以便于输出x中的下一个元素
end
fprintf('\n ') %该行到尽头了,所以换行
end
方法2:巧用计数器
clear
k=0; %k表示当前行内输出到第几个元素了,初始值为0
jsq=1; %jsq表示每一行元素所允许的元素总数,初始值为1
for n=1:55
fprintf('%4d ', n )
k=k+1; %每输出一个元素,k加1
if k==jsq %如果这一行数到了尽头
fprintf('\n ') %该行到尽头了,所以换行
jsq=jsq+1; %下一行的元素总数目加1
k=0; %k置0,以便于下一行开始时重新计数
end
end
课堂练习2:(1)采用randi([1,300],[10,20])生成一个10*20的随机整数矩阵A;(2)把A中能被3或5或7整除的所有元素归类到数组x中,剩余的元素归类到数组y中,输出x,y,并统计数组x与y的元素的数目。(3)把x中所有可以被3整除的元素替换成0。
方法1:for循环
%方法1:for循环
clear
A=randi([1,300],[10,20])
[row col]=size(A)
k1=0; %数组x的计数器
k2=0; %数组y的计数器
x=[ ]; %数组x的初始化为空数组
y=[ ]; %数组y的初始化为空数组
for n=1:row %遍历所有行
for m=1:col %遍历所有列
if mod(A(n,m),3)==0|mod(A(n,m),5)==0|mod(A(n,m),7)==0
%如果元素A(n,m)能被3或5或7整除,则x的计数器k1自加1,并把A(n,m)扔进x里
k1=k1+1;
x(k1)=A(n,m); %也可以写作:x=[ x, A(n,m) ];
else
%如果元素A(n,m)不能被3或5或7整除,则y的计数器k2自加1,并把A(n,m)扔进y里
k2=k2+1;
y(k2)=A(n,m); %也可以写作:y=[ y, A(n,m) ];
end
end
end
x
y
num_x=numel(x)
num_y=numel(y)
% % 把x中所有可以被3整除的元素替换成0。
for k=1:num_x
if mod(x(k),3)==0
x(k)=0;
end
end
x
方法2:向量化编程
%方法2:向量化编程
clear
A=randi([1,300],[10,20])
loc=(mod(A,3)==0|mod(A,5)==0|mod(A,7)==0)
x=A(loc)'
y=A(~loc)'
num_x=numel(x)
num_y=numel(y)
x(mod(x,3)==0)=0;
x
========================================
========================================
Tips1:程序运行的耗时记录方法
TIC
operations; %操作
TOC
简单地说,tic和toc是用来记录matlab命令执行的时间
tic用来保存当前时间,而后使用toc来记录程序完成时间。显示时间单位:秒
========================================
Tips2:算法优化——剪枝算法
一:剪枝策略的寻找的方法
1)微观方法:从问题本身出发,发现剪枝条件
2)宏观方法:从整体出发,发现剪枝条件。
3)注意提高效率,这是关键,最重要的。
总之,剪枝策略,属于算法优化范畴;通常应用在DFS 和 BFS 搜索算法中;剪枝策略就是寻找过滤条件,提前减少不必要的搜索路径。
二:剪枝算法(算法优化)
1、简介
在搜索算法中优化中,剪枝,就是通过某种判断,避免一些不必要的遍历过程,形象的说,就是剪去了搜索树中的某些“枝条”,故称剪枝。应用剪枝优化的核心问题是设计剪枝判断方法,即确定哪些枝条应当舍弃,哪些枝条应当保留的方法。
2、剪枝优化三原则: 正确、准确、高效
搜索算法,绝大部分需要用到剪枝.然而,不是所有的枝条都可以剪掉,这就需要通过设计出合理的判断方法,以决定某一分支的取舍. 在设计判断方法的时候,需要遵循一定的原则.
剪枝的原则
1) 正确性
正如上文所述,枝条不是爱剪就能剪的. 如果随便剪枝,把带有最优解的那一分支也剪掉了的话,剪枝也就失去了意义. 所以,剪枝的前提是一定要保证不丢失正确的结果.
2)准确性
在保证了正确性的基础上,我们应该根据具体问题具体分析,采用合适的判断手段,使不包含最优解的枝条尽可能多的被剪去,以达到程序“最优化”的目的. 可以说,剪枝的准确性,是衡量一个优化算法好坏的标准.
3)高效性
设计优化程序的根本目的,是要减少搜索的次数,使程序运行的时间减少. 但为了使搜索次数尽可能的减少,我们又必须花工夫设计出一个准确性较高的优化算法,而当算法的准确性升高,其判断的次数必定增多,从而又导致耗时的增多,这便引出了矛盾. 因此,如何在优化与效率之间寻找一个平衡点,使得程序的时间复杂度尽可能降低,同样是非常重要的. 倘若一个剪枝的判断效果非常好,但是它却需要耗费大量的时间来判断、比较,结果整个程序运行起来也跟没有优化过的没什么区别,这样就太得不偿失了.
3、分类
剪枝算法按照其判断思路可大致分成两类:可行性剪枝及最优性剪枝.
3.1 可行性剪枝 —— 该方法判断继续搜索能否得出答案,如果不能直接回溯。
3.2 最优性剪枝
最优性剪枝,又称为上下界剪枝,是一种重要的搜索剪枝策略。它记录当前得到的最优值,如果当前结点已经无法产生比当前最优解更优的解时,可以提前回溯。
========================================
========================================
例 : 编程找出100之内所有的勾股数。
满足 x^2+y^2=z^2 的一组正整数(x, y , z)称为一组勾股数。
如:3,4,5
未优化:
clear
N=100; %找到N之内的所有勾股数
num=0; %num表示目前已经找到组数
S=[ ]; %数组S用来存放找到的勾股数,每一行存放一组;
tic %开始计时
for z=1:N %z的范围为1:N
for x=1:N %x的范围为1:N
for y=1:N %y的范围为1:N
if x^2+y^2==z^2
if x<y %只保留x<y的情况,如4,3,5和3,4,5都符合,但我们只要后者这组数
num=num+1; %符合条件则计数器加1
S(num,1:3)=[x,y,z]; %把[x,y,z]扔到数组S的第num行,也可写作 S=[S ; x,y,z];
%fprintf('x=%d ,y=%d,z=%d \n',x,y,z) %如果要打印出来,可以用这句
end
end
end
end
end
toc %计时结束
num %显示找到的勾股数的组数
S %显示存放所有找到的勾股数的数组S
初步优化:(剪枝)
clear
N=100; %找到N之内的所有勾股数
num=0; %num表示目前已经找到组数
S=[ ]; %数组S用来存放找到的勾股数,每一行存放一组;
tic %开始计时
for z=5:N %z的范围为5:N
for x=3:z-2 %x的范围为3:z-2
for y=x+1:z-1 %y的范围为x+1:z-2
if x^2+y^2==z^2
num=num+1; %符合条件 则计数器加1
S(num,1:3)=[x,y,z]; %把[x,y,z]扔到数组S的第num行,也可写作S=[S ; x,y,z];
%fprintf('x=%d ,y=%d,z=%d \n',x,y,z) %如果要打印出来,可以用这句
end
end
end
end
toc %计时结束
num %显示找到的勾股数的组数
S %显示存放所有找到的勾股数的数组S
继续优化:(剪枝)
clear
N=100; %找到N之内的所有勾股数
num=0; %num表示目前已经找到组数
S=[ ]; %数组S用来存放找到的勾股数,每一行存放一组;
tic %开始计时
for z=5:N
for x=3:fix(z/sqrt(2))
for y=(x+1) : fix(sqrt(z^2-x^2))
if x^2+y^2==z^2
num=num+1; %符合条件 则计数器加1
S(num,1:3)=[x,y,z]; %把[x,y,z]扔到数组S的第num行,也可写作S=[S ; x,y,z];
%fprintf('x=%d ,y=%d,z=%d \n',x,y,z) %如果要打印出来,可以用这句
end
end
end
end
toc %计时结束
num %显示找到的勾股数的组数
S %显示存放所有找到的勾股数的数组S
% 设N=3000,再比较以上三段代码的运行时间的差异?
编程练习:
编程验证,是否存在n1,n2,n3,n4,n5 这5个大于等于2的自然数(范围均在2--200之间),使得下式成立?

(可假设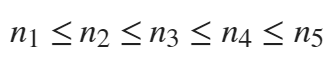 )
)
要求:比比看,谁的程序用时最少?
例: 求s的值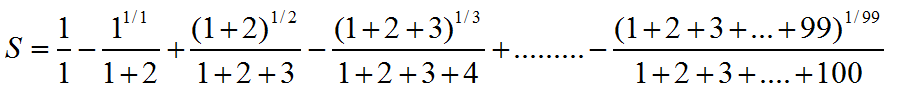
%for循环加sum( ) 函数
clear all
s=1; %s初始值
flag=-1; %正负交替标识,初始化
for k=1:99
s=s+flag*(sum([1:k])^(1/k))/sum([1:k+1]);
flag=-1*flag;
end
s
%方法2:
clear all
s=1;
for k=1:99
s=s+(-1)^k*(sum([1:k])^(1/k)/sum([1:k+1]));
end
s
例:![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B2%7D) 的连分数表示方法如下,编程计算
的连分数表示方法如下,编程计算![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B2%7D) 。
。
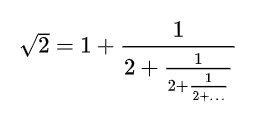
①如果舍弃上述等式右侧分母中的一部分,于是可得:
![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B2%7D%3D1.5)
②如果舍弃上述等式右侧分母右侧一部分,于是:
![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%7D%7D%3D1%2B%5Cfrac%7B2%7D%7B5%7D%3D1.4)
③再舍弃上述等式右侧分母右侧一部分,于是:
![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%7D%7D%7D%3D1%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B2%7D%7B5%7D%7D%3D1%2B%5Cfrac%7B5%7D%7B12%7D%3D1.417)
④接下来再舍弃上述等式右侧分母右侧一部分,于是:
![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%7D%7D%7D%7D%3D1%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B5%7D%7B12%7D%7D%3D1.414)
⑤再舍弃上述等式右侧分母右侧一部分,于是:
![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%7D%7D%7D%7D%7D%3D1%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B1%7D%7B2%2B%5Cfrac%7B5%7D%7B12%7D%7D%7D%3D1.4143)
⑥一直重复的话,精度就会越来越高。
clear
s=1/2; %为等式右边1之后的那个连分式的初始值
for n=1:10 %算10层连分式
s=1/(2+s);
end
two_sqrt=1+s %最终求出根号2
vpa(two_sqrt,20) %本程序算出的根号2,显示小数点后20位
vpa(sqrt(2),20) %sqrt函数算出的根号2,,显示小数点后20位,比较两者精度
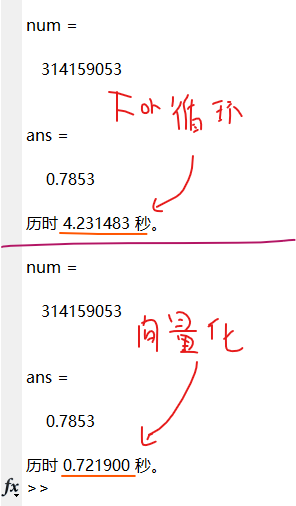
3.加快程序运行的技巧
(1)向量化编程

%蒙特卡洛法计算圆周率
tic
m=0; %m为落于半径为1的圆内的点数
n=1000000; %n为总点数
for i=1:n
x=rand(1); %生成第i个点的x,y坐标
y=rand(1);
if x*x+y*y<=1 %判断第i个点在不在圆内
m=m+1; %在圆内的话,计数器m加1
end
end
pai=4*m/n
toc
时间已过 0.512270 秒。
采用向量化编程:
tic
n=1000000; %n为总点数
x=rand(1,n);
y=rand(1,n);
r=x.^2+y.^2;
z=r(r<=1);
m=numel(z);
pai=4*m/n
toc
时间已过 0.037208 秒。
很明显,采用向量化编程,运行时间节省了十几倍!
(2)如果有多重循环,则注意循环的顺序,应该外层少,内层多。
生成100*100000的希尔伯特矩阵。比较两种循环的效率。
%n表示行,m表示列
%-----------------------------------------------------------------
%外层循环少,内层循环多
clear
tic
for n=1:100 %外层循环少,内层循环多
for m=1:100000
H(n,m)=1/(n+m-1);
end
end
toc
%-----------------------------------------------------------------
%外层循环多,内层循环少
clear
tic
for m=1:100000 %外层循环多,内层循环少
for n=1:100
H(n,m)=1/(n+m-1);
end
end
toc
(3)预先分配数组和矩阵的容量(而不是让系统动态分配)

总结:
(1)使用循环语句应尽量预先分配内存空间。
(2)优先使用向量化思维编程,其次才是采用循环。
例:预分配内存的例子
若一个变量所需要的内存空间是一个可预测的定值,我们应尽量提前为其分配内存空间.


%方法1: 没有预先分配内存
clear
tic
k=3000
for n=1:k
for m=1:k
H(n,m)=1/(n+m-1);
end
end
toc
程序输出: 时间已过14.056814 秒。
%方法2: 预先为变量分配内存空间
clear
tic
k=3000
H=zeros(k);
for n=1:k
for m=1:k
H(n,m)=1/(n+m-1);
end
end
toc
程序输出: 时间已过0.210248秒。
方法3:向量化编程
clear
tic
k=3000
x=[1:k]';
row=repmat(x,1,k);
y=[1:k];
col =repmat(y,k,1);
H=1./(row+col-1);
toc
程序输出: 时间已过 0.060235秒。
=========================================
练习1
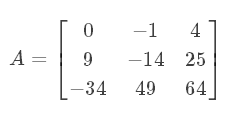
编程把矩阵A中所有小于0的数都改为0
1. 纯for循环
A = [0, -1, 4 ; 9, -14, 25 ; -34, 49, 64]
for n = 1:3
for m = 1:3
if A(n,m) < 0
A(n,m) = 0;
end
end
end
2. 布尔数组引用法
A = [0, -1, 4 ; 9, -14, 25 ; -34, 49, 64]
y= A<0;
A(y) = 0;
A
3.find函数法
A = [0, -1, 4; 9, -14, 25; -34, 49, 64]
[x,y]=find(A<0)
x=x'
y=y'
for n=1:length(x)
A (x(n),y(n))=0;
end
A
==================================
==================================
作业1:编程输出类似如下的乘法口诀表
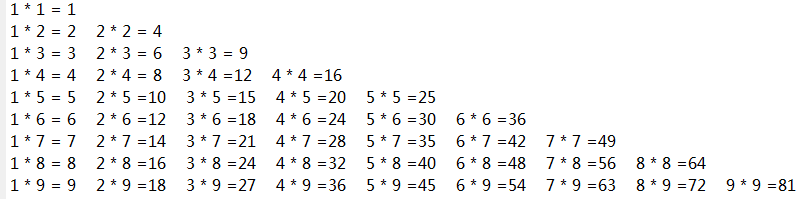
作业2:文字谜:山青与水秀 x 美 = 秀水与青山
其中“山青与水秀美”为1-9中的其中6个不同的数字,把这个6个数字编程找出来。
作业3:求100-999之间的全部水仙花数。
水仙花数是指:一个三位数,其各位数字立方和等于该数本身。例如:370=33+73+03.这就说明370是一个水仙花数。
作业4:信用卡校验
当你输入信用卡号码的时候,有没有担心输错了而造成损失呢?其实可以不必这么担心,因为并不是一个随便的信用卡号码都是合法的,它必须通过Luhn算法来验证通过。
该校验算法的过程:
1、从卡号最后一位数字开始,逆向将奇数位(1、3、5等等)相加,得到s1
2、从卡号最后一位数字开始,逆向将偶数位数字,先乘以2(如果乘积为两位数,则将其减去9),再求和,得s2
3、将奇数位总和加上偶数位总和,既s=s1+s2,得出的s应该可以被10整除!如果S不能被10整除,则卡号是错误的。
例如,卡号:5432123456788881 (其逆向为:1888876543212345)
逆向奇数位为 1 8 8 6 4 2 2 4 ,求和 = 35
逆向偶数位乘以2(有些要减去9)的结果:7 7 5 1 6 2 6 1,求和 = 35。
最后 35 + 35 = 70 可以被10整除,则认定校验通过。
请编写一个程序,从标准输入获得卡号,然后判断是否校验通过。
通过显示:“卡号正确”,否则显示“卡号错误”。
比如,输入:356827027232780
程序输出:卡号正确
提示答案:
x=input('请输入卡号,并以单引号引住这串数字:')
y=x([end:-1:1]) %把字符数组x反向后给y
s_even=0; %偶数位的和的计数器
s_odd=0; %奇数位的和的计数器
for n=1:2:L %处理奇数位
t1=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
??
end
for n=2:2:L %处理偶数位
t2=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
??
end
total=(s_odd+s_even)
if ??
fprintf('卡号正确 \n');
else
fprintf('卡号错误 \n');
end
==================================================================
作业5:计算圆周率
利用下列的公式求圆周率PI的值。至少选择以下公式中的2个编程计算圆周率的值。(注意,如果公式里出现阶乘,不要计算太多项,否则计算时间会过长)
这里给出第一个公式的求解代码:
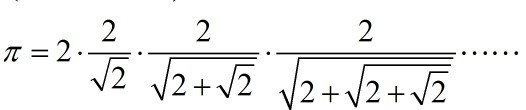
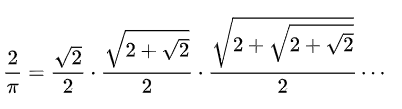
%代码如下:
clear
t=1/2;
x1=sqrt(t);
y1=sqrt(t+t*x1);
for ii=1:20
x1=x1*y1;
y1=sqrt(t+t*y1);
end
p1=2/x1; %p1为我们用公式计算的圆周率
vpa(p1) %vpa显示p1的精确值
vpa(pi,50) %作为对比,用vpa显示真实的π的前50位
计算前20项,已经精确到小数点后12位。

提示:以下公式编程时可能会用到阶乘,MATLAB里阶乘的函数为 factorial( )
factorial(n) 等价于 prod([1:n])
factorial(12) % 12的阶乘已经很大了
ans =
479001600
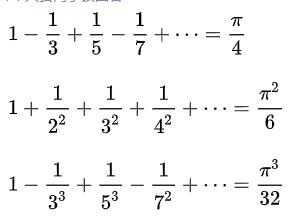
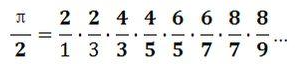
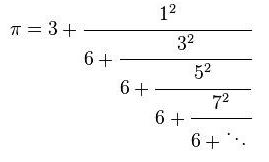
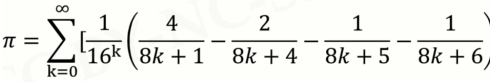
============================================
补充知识:跳出循环的几种方式。

在写脚本的时候用到这些功能并不多,但是偶尔还是需要用到,每次都得重新查……这次整理一下记录几个常见的控制程序走停的函数pause、input、error、warning、break、quit、exit、return。
1、pause
在执行脚本文件过程中可以让脚本暂停;
用法:
①pause:暂停,等待用户按下任意键继续;
②pause(n):暂停n秒,然后继续。
2、input
input()也可以让脚本暂停,等待用户输入后继续执行脚本;
用法:
① y = input(‘请输入:’); 只能输入数字;
② y = input(‘请输入:’, ‘s’); 将输入转化为字符串;
reply = input('Do you want more? Y/N [Y]:','s');
if isempty(reply)
reply = 'Y';
end
3、error/warning
报错并退出当前脚本;
用法:
error(’ 报错提示’);
error('输入不符合要求')
warning('输入不符合要求')
两者用法相似,不过error会终止程序,warning并不会。
4、break
break函数只能在while和for循环里使用,作用是跳出当前循环,直接开始执行循环之后的语句,注意如果有多个嵌套循环,break只能跳出最里边的。
a=0;
for i=1:5
for j=0.1:0.1:0.3
if i>4
break;
end
disp(j);
end
disp(i)
end
5、quit、exit
quit和exit的功能是一样的,都是退出matlab,注意与error的区别,error只是退出执行脚本,而quit和exit直接退出了matlab程序(软件)。
终止Matlab正在运行的程序,一般有三种方法。
快捷键
关闭Matlab程序
在脚本中添加代码
1、快捷键
Ctrl+C
Ctrl+break
Ctrl+Alt+break
如果是在服务bai器上跑的代码的话,按完快捷键之后有时候需要等一小会,程序才会停。
2、关闭Matlab程序
有时候跑Matlab内存占用过高,会有死机的情况,这时候可以关闭Matlab优化程序。关闭Matlab可以点x,也可以Ctlr+Alt+Delete,启动任务管理器强制关闭。
3、添加代码
code 含义
quit 终止 MATLAB程序。quit 函数不会自动保存工作区。
quit cancel 适用于 finish.m 脚本,可取消退出。它在其他地方无效。
quit force 绕过 finish.m 并终止 MATLAB。当 finish 脚本不允许您退出时,可使用此语法覆盖脚本。
quit(code) 返回指定值作为 MATLAB 退出代码。
quit(code,“force”) 绕过 finish.m 并终止 MATLAB,同时返回退出代码。
return 在函数或脚本到达末尾之前以编程方式停止其执行
示例: quit(0,"force") 注意:相当于是退出了Matlab软件,不好用的。
6、return
常用在自定义function里边,通常与if…else…一起用,如果满足if了,可以用return提前返回,不必再执行if…else…后的语句。
function d = det(A)
if isempty(A)
d = 1;
return
else
...
end
...
当然,普通的脚本里(非function)也可以用,如使用多重for循环来搜索某个答案的时候,如果希望搜索到一个答案就跳出所有循环,就可以采用:
for ...
for...
for...
if 符合某某条件
return
end
课外练习1:求全体自然数的立方的倒数之和
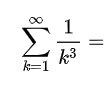
1734年,27岁的欧拉计算出全体自然数的平方的倒数和是 ![[公式]](https://www.zhihu.com/equation?tex=%5Cpi%5E2%2F6) :
:
![[公式]](https://www.zhihu.com/equation?tex=1%2B%5Cfrac%7B1%7D%7B2%5E2%7D%2B%5Cfrac%7B1%7D%7B3%5E2%7D%2B%5Cfrac%7B1%7D%7B4%5E2%7D%2B%5Cfrac%7B1%7D%7B5%5E2%7D%2B...%3D%5Cfrac%7B%5Cpi%5E2%7D%7B6%7D)
这个成就使欧拉一下子名声大噪,成为数学家中的社会名人。以上这个问题后来以欧拉的家乡瑞士巴塞尔命名,称为“巴塞尔问题”。
欧拉自己也很兴奋,他一鼓作气,计算了指数为偶数,直到26次方的自然数幂次倒数和的情况:
![[公式]](https://www.zhihu.com/equation?tex=1%2B%5Cfrac%7B1%7D%7B2%5E4%7D%2B%5Cfrac%7B1%7D%7B3%5E4%7D%2B%5Cfrac%7B1%7D%7B4%5E4%7D%2B%5Cfrac%7B1%7D%7B5%5E4%7D%2B...%3D%5Cfrac%7B%5Cpi%5E4%7D%7B90%7D)
![[公式]](https://www.zhihu.com/equation?tex=1%2B%5Cfrac%7B1%7D%7B2%5E6%7D%2B%5Cfrac%7B1%7D%7B3%5E6%7D%2B%5Cfrac%7B1%7D%7B4%5E6%7D%2B%5Cfrac%7B1%7D%7B5%5E6%7D%2B...%3D%5Cfrac%7B%5Cpi%5E6%7D%7B945%7D)
...
![[公式]](https://www.zhihu.com/equation?tex=1%2B%5Cfrac%7B1%7D%7B2%5E%7B26%7D%7D%2B%5Cfrac%7B1%7D%7B3%5E%7B26%7D%7D%2B%5Cfrac%7B1%7D%7B4%5E%7B26%7D%7D%2B%5Cfrac%7B1%7D%7B5%5E%7B26%7D%7D%2B...%3D%5Cfrac%7B%5Cpi%5E%7B26%7D%5Ccdot+2%5E%7B24%7D%5Ccdot+76977927%7D%7B27%21%7D)
那么问题就来了,指数为3的情况下,结果如何呢?这个问题意外地困难。欧拉一生中曾经多次挑战这个问题,找到了许多相关结果,比如奇数的3次幂的交错级数情况:
![[公式]](https://www.zhihu.com/equation?tex=1-%5Cfrac%7B1%7D%7B3%5E3%7D%2B%5Cfrac%7B1%7D%7B5%5E3%7D-%5Cfrac%7B1%7D%7B7%5E3%7D%2B%5Cfrac%7B1%7D%7B9%5E3%7D-...%3D%5Cfrac%7B%5Cpi%5E3%7D%7B32%7D)
然而欧拉始终不能对自然数立方倒数和问题找出一个“简单”的确切答案。
1785年,在欧拉去世后2年出版的论文中,可以看到欧拉在生命中的最后岁月仍在尝试解决这个问题。欧拉承认:“我用过如此多的方法寻找自然数的立方倒数和,然而所有方法均徒劳无功。以上(积分式)的方法也没有产生任何结果,所以看上去放弃(研究这个问题)是正确选择...”
近200年后,1978年,Roger Apery证明:全体自然数的立方倒数和是一个无理数。他证明的结论并不让人吃惊,让数学家吃惊的是,对这个问题的研究居然还能产生一些进展,因为欧拉都放弃了!现在全体自然数的立方倒数和就被被称为“Apery常数”。
课外练习2:高斯圆问题
高斯圆问题,又叫圆内整点问题。

%For循环法
clear
tic
r=10000;
r2=r^2;
x=-r:r;
y=-r:r;
num=0;
for k1=x
for k2=y
if k1^2+k2^2<=r2
num=num+1;
end
end
end
num
num/(2*r+1)^2
toc
%%
%向量化
clear
tic
r=10000;
r2=r^2;
x=-r:r;
y=-r:r;
num=0;
p1=repmat(x,2*r+1,1);
p2=repmat(y',1,2*r+1);
loc=p1.^2+p2.^2<=r2;
num=sum(loc(:))
num/(2*r+1)^2
toc
例:Generate a vector like 1,2,2,3,3,3,4,4,4,4
So if n = 3, then return
[1 2 2 3 3 3]
And if n = 5, then return
[1 2 2 3 3 3 4 4 4 4 5 5 5 5 5]
n=5;
s =[ ];
for k=1:n
s=[s , k*ones(1,k)];
end
s
课外练习3:自然数平方根的连分数表达:

clear
N=2; %如,计算根号2的连分式表达
syms n a temp n_sqt
n=sym(N)
a=sym(fix(sqrt(N)))
temp=sym(0);
for k=1:15 %嵌套15层连分式
temp=(n-a^2)/(2*a+temp);
end
n_sqt=a+temp %显示根号2的连分时近似表达
vpa(n_sqt,40)
vpa(sqrt(N),40)






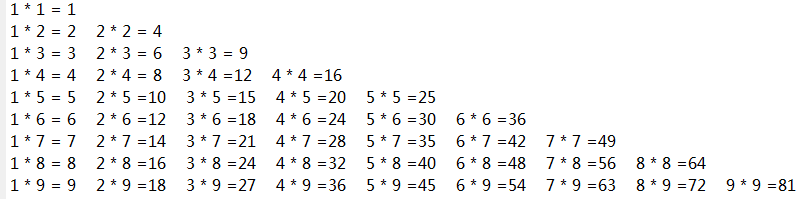




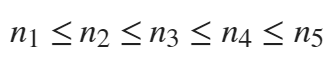 )
)