1.编程，求圆周率Pi中前100万位里，是否出现你的生日（六位生日，如1999年3月12日，则认为生日为 990312），如果出现则具体出现了多少次，分别出现是小数点后的多少位？

clc

str1='990312'         %要找的字符串

n=length(str1);      %测量这个字符串的长度

pi_str=char(vpa(pi,100000));   %把pi显示100000位后，再转换为字符串

M=length(pi_str);                   % 测量这个字符串的长度

count=0;                 %计数器，用来记录找到了多少次符合条件的情况

for i=3:M-n              %从字符串第三位开始寻找，因为前两位为: 3. 

      if  pi_str( i : (i+n-1) )==str1

           count=count+1;       %若if成立，则说明找到了符合要求的。计数器加1

           fprintf('第%d次找到符合条件，其在小数点后%d 位 \n' ,count , (i-2) )  

      end

end

fprintf(' \n 所搜索的字符串在pi里共出现了%d次 \n' ,count )  

=================================

还可以用findstr函数，查找字符串中的子串。

例：

>>str='ancdr'

>>findstr (str,'dr')

ans =

     4

strcat函数的作用：连接两个字符串。

例：

s1='I'     ;s2=', '    ;s3='L'     ;s4='o'    ;s5='v';

s6='e'    ;s7=', '    ;s8='y'     ;s9='o'    ;s10='u';

s=strcat(s1,s2,s3,s4,s5,s6,s7,s8,s9,s10)

练习：将一个大于等于3的数分成三个正整数（大于0）相加有多少种分法？

%完全没有任何优化

M=30

total=0

tic

for k1=1:M

    for k2=k1:M

        for k3=k2:M

            

            if  M==k1+k2+k3               

                 fprintf('%d + %d + %d = %d \n',k1,k2,k3,M)  %注释掉该行，可看出优化与否的差异 

                  total=total+1;          

            end

            

        end

    end

end

toc

fprintf(' 数字%d 的解有%d组  \n',M,total)

==========================================

%优化后的算法

M=30

total=0

tic

for k1=1:fix(M/3)                %K1最多分三分之一

    for k2=k1:fix((M-k1)/2)   %K2下限是k1,上限最多分剩余的2分之一

        

         k3=M-k1-k2;           

         fprintf('%d + %d + %d = %d \n',k1,k2,k3,M)  %注释掉该行，可看出优化与否的差异    

         total=total+1;

 

    end

end

toc

fprintf(' 数字%d 的解有%d组  \n',M,total)

===================================================

%函数化

function [A,total] = M_3(M)

A=[];         %用矩阵A来装发现的解，每一行存一组解

total=0;

for k1=1:fix(M/3)

    for k2=k1:fix((M-k1)/2)

        

        k3=M-k1-k2;

        total=total+1;            %计数器total，可以代表矩阵A的行数

        A(total,:)=[k1,k2,k3];   %把k1,k2,k3水平方向拼接成一个数组给A的第total行

    end

end

end

2.图像的中间值滤波。

 所谓中央值滤波器，就是将滤波器范围内的像素的灰度值，进行排序，选出中央值作为这个像素的灰度值。同理可解释最大值滤波器与最小值滤波器。

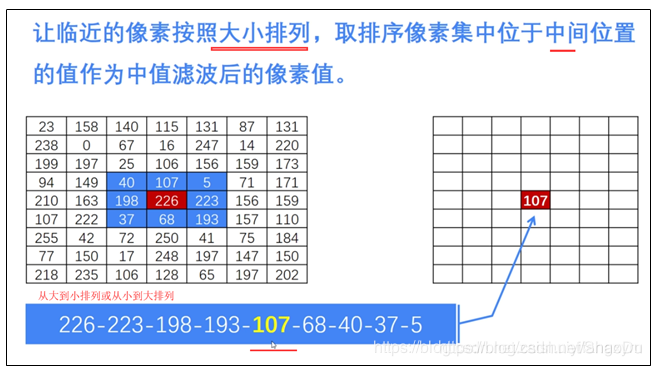
再举个例子，下面是一副图像中的一个点及其邻域上的点，上面的值代表其灰度值。首先将这9个像素值从小到大排列，依次是：90,110,120,150,165,200,210,230,255，中值为165，最大值是255，最小值是90。原本该点的灰度值应该是150，如果采用中值滤波器的话，则会用165来取代150，即该点的灰度值变成了165；如果是最小值滤波器的话，则该点的灰度值变成90；如果是最大值滤波器的话，则该点的灰度值变成255。

我们将一幅图像添加椒盐噪声，然后尝试着用中央值滤波器去除。

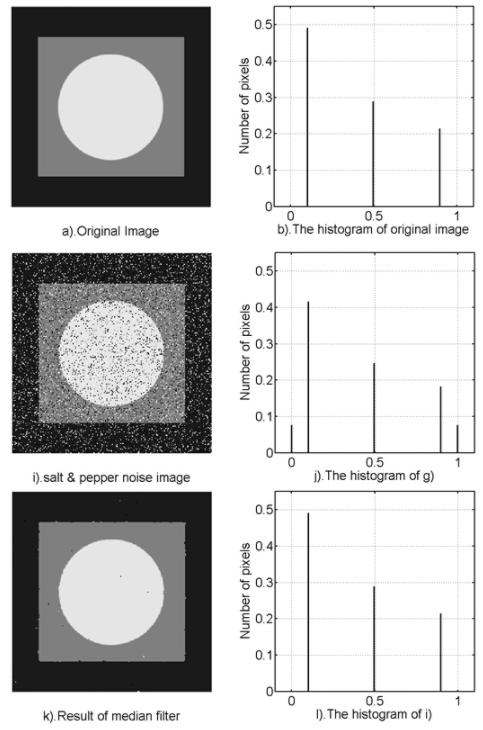
从直方图中，可以看出，中央值滤波器对于椒盐噪声，有很好的去噪作用。

%给图像加噪声

>> i=imread('E:\科研\数字图像处理\bird1.jpg');

>> j1=imnoise(i,'salt & pepper',0.02);

>> imshow(j1)

>> imwrite(j1,'E:\科研\数字图像处理\bird1_saltpepper.png')

2.某个数的三次方是4位数，四次方是6位数，且其三次方和四次方这两个数正好把0-9这10个数字用完，不多不少，求这个数是多少？

分析：

（1）4位数区间为：1000-9999，开3次方为：10-21.5436，取10-21

（2）6位数区间为：100000-999999，开4次方为：17.7828-31.6228，取18-31

 由上可知：这个数位于18-21之间

clc

 for i=18:21

      x=num2str(i^3)    %把数字转为字符串

      y=num2str(i^4)    %把数字转为字符串

      z=strcat(x,y)          %通过strcat函数合并两个字符串

      z=sort(z)                %对这个字符串从小到大排序

      if  z=='0123456789' 

          fprintf('找到符合条件的I=%d, 其3次方为%d,4次方为%d \n' , i , i^3 ,i^4 )

          break

      end

 end

3：求两个整数X1,X2的最大公约数：

x1=input('x1=')

x2=input('x2=')

if  x1<=x2

    smaller=x1;

else

    smaller=x2;

end

for  i=1:smaller

      if  (rem(x1,i)==0)&(rem(x2,i)==0)

           gys=i;

      end

end

fprintf('%d  和 %d 的最大公约数为%d \n' , x1 , x2 ,gys )

作业1：百钱买白鸡问题

1，问题描述：

公鸡每只5元，母鸡每只3元，三只小鸡1元，用100元买100只鸡，问公鸡、母鸡、小鸡各多少只？

2，算法分析：

利用枚举法解决该问题，以三种鸡的个数为枚举对象,分别设为mj,gj和xj，用三种鸡的总数 （mj+gj+xj=100）和买鸡钱的总数（1/3*xj+mj*3+gj*5=100）作为判定条件，穷举各种鸡的个数。

%原始代码：

for  m=0:20

     for  n=0:33

         for  k=0:3:300

             if  (m*5+3*n+(k/3)==100)&(m+n+k==100)

                  fprintf('公鸡%d个，母鸡%d个，小鸡%d个\n',m,n,k)

             end

         end

     end

end

%改进后：

for m=0:20

        for k=0:3:99

            n=100-m-k;

            if  (m*5+3*n+(k/3)==100)&(n>=0)

                 fprintf('公鸡%d个，母鸡%d个，小鸡%d个\n',m,n,k)

            end

        end 

end

作业2：给一个无限长的自然数构成的字符串

S: 12345678910 111213141516171819 202122232425….....，

它是由所有自然数从小到大依次排列起来的，任意给一个数字串STR1(如751)，编程求出它第一次出现在S中的位置。

clc

str1='751'             %要找的字符串

n=length(str1);      %测量这个字符串的长度

S=[];                     %S用来存储即将生成的S序列

K=1;                    %设k为数组S的位置索引变量，如k=11时，S（11）=0

S=char(S);            %把S字符化

for i=1:1000         %生成这个字符串,相当于从1写到1000

      L=length(num2str(i));  %测量I是几位数，如i=231时，L=3;

........补齐代码，完成数组S的建立

end

M=length(S)      %测量数组s的长度

for i=1:M-n+1    %开始匹配要找的字符串str1位于S中的第几位？

       if      

........补齐代码，如果符合条件，则打印输出，说明在第几位找到了

       end

 end

效果：

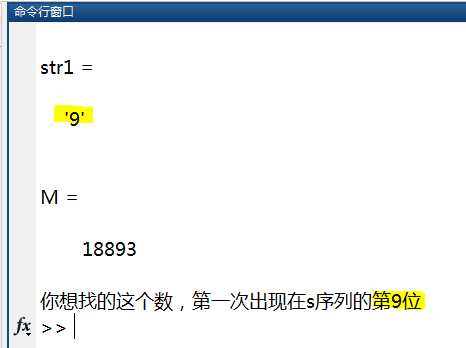
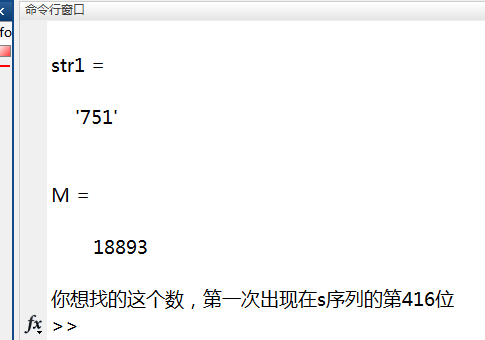
作业3：反转字符串 

给定一个字符串句子，反转句子中每一个单词的所有字母，同时保持空格和最初的单词顺序。字符串中，每一个单词都是由空格隔开，字符串中不会有多余的空格。

样例

输入: "Let's take LeetCode contest"
输出: "s'teL ekat edoCteeL tsetnoc"

作业4：最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],

输出: 6

解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

很多人对这道题最开始都会有一个误区，就是 只要将连续的正数相加就肯定是最大的，这种思想当然是有问题的 最简单的例子 1, 2, 3, -99, 100000 如果用刚才那样想法求出的最大和是6，但是答案肯定是不对的,应该是最后一项数

所以这就引出了一种思想：

如果当前和大于0，则加上下一个数（当前和是正的 对后面的求和“有益处”）

如果当前和小于或等于0，则将下一个数赋给当前和

最后比较当前和与存储最大值的变量 取最大值

% str=[-2,1,-3,4,-1,2,1,-5,4,3,-1,2,-5,2,-3,4];

str=randi([-30,30],[1,100])

s_temp=0;

s_all=0;

for  k=str

      if   s_temp>0  

%如果过去为正资产，则保留过去，同时拥抱未来。哪怕未来是负的，只要这个负不是很严重到可以把过去的正全部抵消，则一直保留过去，拥抱未来。

           s_temp=s_temp+k;

      else   

%如果之前的s_temp位负资产，则舍弃过去，拥抱未来（哪怕未来也是负的，未来一个负总比过去的负加上未来的负强，如果未来是正的，更要拥抱）

           s_temp=k;

     end

     s_all=max(s_all,s_temp); 

       %不断在当前的最大值s_temp和历史上的最大值s_all中选择其中最大的，作为新的史上最大的值。

end

s_all

==================================

课外小知识：

但现在我把数字换成  会如何？找一个方程，它有一个解  ，但是方程本身不能出现  ？你是不是一下子傻了？你不能说  这种方程，因为我规定方程里不能有  。这里面你就能看出，一个  与  的本质区别，  不能用若干根号的加减乘除组合表示出来的，所以它不能成为我们 课堂上所学的那种代数方程的根。

代数方程就是我们在学校里学的一元二次方程的扩展为一元n次方程。这里面n是自然数，且方程的系数都是有理数。

而显然  和  都不能用若干根号表示出来，否则我们很可能就不用引入  和  这两个符号了对不对？因此数学家定义了，那种可以是代数方程根的数为“代数数”，这其中包括了所有有理数和那种可以用若干根号组合表示出来的无理数。而不可以的成为代数方程根的数，就叫做“超越数”。

那你可能又有问题了，区分代数数和超越数有意义吗？没有意义的话，就不应该引入对不对？你这个思路非常对，那么数学家既然定义了超越数，那必然有用。

首先数学家发现，“几乎”所有的实数都是超越数。哇，这是不是很吃惊？首先，这里的“几乎”这次词是数学用语，如果你不知道“几乎”的含义，那你可以搜索我之前的一期题为“我几乎懂了”的节目。

“几乎”所有的实数都是超越数这句话告诉我们：实数里超越数是占主要部分的，代数数与超越数相比是可以忽略不计的。对这个结论，了解一点无穷基数理论的听众可以这样理解：我们知道有理数是可数集，也就是我们有一个方法可以把所有有理数一个一个写下来，写成一个序列，这个序列包含所有有理数。这样感觉它们就可以数数一样，所以称为“可数”集。

然后数学家还发现如果把有理数扩展到代数数，仍然是可数的，代数数仍然是可以排队排出来的。那我们已经知道实数是不可数，那么结论就只有超越数是真正不可数的，所以说“几乎所有实数都是超越数”。这是很反直觉的对不对？所以定义超越数就太有必要了，原来我们一直讨论的实数，其实基本都是超越数啊。

但是，虽然我们知道“几乎所有实数都是超越数”，证明一个数字是超越数却非常难。比如你要证明  不能用若干根号表示出来，你怎么证明呢？其实到1768年，才第一次证明  是无理数，而证明  是超越数又过了100多年，要迟到1882年。也正因为证明了  是超越数，人类才彻底解决了古希腊三大几何难题中最难的一个“化圆为方”问题。

其原因在于我们已经证明尺规作图只能作出特定形状的一些代数数长度的线段，超越数长度的线段是不可能作出来的。所以证明pi为超越数，就证明“化圆为方”问题无解。

除了  ，数学家也证明了比如  ,  ，  ，这些数都是超越数。但是目前已经被被证明是超越数的数非常少，倒是很多感觉上必须是超越数的数，我们都还不能证明：比如  ，  ，  ,  ，  ,  等等，这些数是否是超越数，都未能证明。再比如以前节目中提到过的欧拉-马斯刻若尼常数，虽然猜想是超越数，但现在都没能证明这个数字是无理数。

由此可见，超越数虽然多，但是却很神秘。

以上我们说明了无理数跟无理数还不一样，那有没有办法更精细的对无理数分类的，比一比无理数中谁的“无理”程度“更高”呢？还真有人真么做了。1932年，荷兰数学家库尔特·马勒就提出了一个实数的“无理性”度量，就是度量一个实数到底“无理”到什么程度，取值范围从0到无穷大的整数。对有理数来说，这个度量值就是0，因为它有理，一点不无理。对根号2来说就是1，这就是无理数里面“无理”程度最小的。而超越数的无理数度量最小是2，比如现在知道  的无理性度量上限是2.5等等。

好了，以上就是简单介绍了一下超越数概念。

总结：不能满足整系数方程a1+a2x+a3x^2+……+a(n+1)x^n=0的数都是超越数。超越数远远比代数数多，代数数只有阿列夫零个，超越数有阿列夫一个。我们乱写一个无理数，100%都是超越数。超越数有a^b(a为非0，1代数数，b为无理代数数),π,e等。对数算不出的都是超越数。还有像0.1010010001……和0.12345678910……等有规律但不循环的数都是超越数。还有刘维尔数。

===================================