什么是算法的时间复杂度?
算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,比如排序就有前面的十大经典排序和几种奇葩排序,虽然结果相同,但在过程中消耗的资源和时间却会有很大的区别,比如快速排序与猴子排序:)。
那么我们应该如何去衡量不同算法之间的优劣呢?
主要还是从算法所占用的「时间」和「空间」两个维度去考量。
时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述。
空间维度:是指执行当前算法需要占用多少内存空间,我们通常用「空间复杂度」来描述。
本小节将从「时间」的维度进行分析。
什么是大O
当看「时间」二字,我们肯定可以想到将该算法程序运行一篇,通过运行的时间很容易就知道复杂度了。
这种方式可以吗?当然可以,不过它也有很多弊端。
比如程序员小吴的老式电脑处理10w数据使用冒泡排序要几秒,但读者的iMac Pro 可能只需要0.1s,这样的结果误差就很大了。更何况,有的算法运行时间要很久,根本没办法没时间去完整的运行,还是比如猴子排序:)。
那有什么方法可以严谨的进行算法的时间复杂度分析呢?
有的!
「 远古 」的程序员大佬们提出了通用的方法:「 大O符号表示法 」,即 T(n) = O(f(n))。
其中 n 表示数据规模 ,O(f(n))表示运行算法所需要执行的指令数,和f(n)成正比。
上面公式中用到的 Landau符号是由德国数论学家保罗·巴赫曼(Paul Bachmann)在其1892年的著作《解析数论》首先引入,由另一位德国数论学家艾德蒙·朗道(Edmund Landau)推广。Landau符号的作用在于用简单的函数来描述复杂函数行为,给出一个上或下(确)界。在计算算法复杂度时一般只用到大O符号,Landau符号体系中的小o符号、Θ符号等等比较不常用。这里的O,最初是用大写希腊字母,但现在都用大写英语字母O;小o符号也是用小写英语字母o,Θ符号则维持大写希腊字母Θ。
注:本文用到的算法中的界限指的是最低的上界。
常见的时间复杂度量级
我们先从常见的时间复杂度量级进行大O的理解:
常数阶O(1)
线性阶O(n)
平方阶O(n²)
对数阶O(logn)
线性对数阶O(nlogn)
-----------------------------------------------------------------------------------------------------
O(1)
无论代码执行了多少行,其他区域不会影响到操作,这个代码的时间复杂度都是O(1)
1void swapTwoInts(int &a, int &b){
2 int temp = a;
3 a = b;
4 b = temp;
5}
O(n)
在下面这段代码,for循环里面的代码会执行 n 遍,因此它消耗的时间是随着 n 的变化而变化的,因此可以用O(n)来表示它的时间复杂度。
1int sum ( int n ){
2 int ret = 0;
3 for ( int i = 0 ; i <= n ; i ++){
4 ret += i;
5 }
6 return ret;
7}
特别一提的是 c * O(n) 中的 c 可能小于 1 ,比如下面这段代码:
1void reverse ( string &s ) {
2 int n = s.size();
3 for (int i = 0 ; i < n/2 ; i++){
4 swap ( s[i] , s[n-1-i]);
5 }
6}
O(n²)
当存在双重循环的时候,即把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²) 了。
1void selectionSort(int arr[],int n){
2 for(int i = 0; i < n ; i++){
3 int minIndex = i;
4 for (int j = i + 1; j < n ; j++ )
5 if (arr[j] < arr[minIndex])
6 minIndex = j;
7
8 swap ( arr[i], arr[minIndex]);
9 }
10}
这里简单的推导一下
当 i = 0 时,第二重循环需要运行 (n - 1) 次
当 i = 1 时,第二重循环需要运行 (n - 2) 次
。。。。。。
不难得到公式:
1(n - 1) + (n - 2) + (n - 3) + ... + 0
2= (0 + n - 1) * n / 2
3= O (n ^2)
当然并不是所有的双重循环都是 O(n²),比如下面这段输出 30n 次 Hello,五分钟学算法:)的代码。
1void printInformation (int n ){
2 for (int i = 1 ; i <= n ; i++)
3 for (int j = 1 ; j <= 30 ; j ++)
4 cout<< "Hello,五分钟学算法:)"<< endl;
5}
O(logn)
1int binarySearch( int arr[], int n , int target){
2 int l = 0, r = n - 1;
3 while ( l <= r) {
4 int mid = l + (r - l) / 2;
5 if (arr[mid] == target) return mid;
6 if (arr[mid] > target ) r = mid - 1;
7 else l = mid + 1;
8 }
9 return -1;
10}
在二分查找法的代码中,通过while循环,成 2 倍数的缩减搜索范围,也就是说需要经过 log2^n 次即可跳出循环。
同样的还有下面两段代码也是 O(logn) 级别的时间复杂度。
1 // 整形转成字符串
2 string intToString ( int num ){
3 string s = "";
4 // n 经过几次“除以10”的操作后,等于0
5 while (num ){
6 s += '0' + num%10;
7 num /= 10;
8 }
9 reverse(s)
10 return s;
11 }
1void hello (int n ) {
2 // n 除以几次 2 到 1
3 for ( int sz = 1; sz < n ; sz += sz)
4 for (int i = 1; i < n; i++)
5 cout<< "Hello,五分钟学算法:)"<< endl;
6}
O(nlogn)
将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logn),也就是了O(nlogn)。
1void hello (){
2 for( m = 1 ; m < n ; m++){
3 i = 1;
4 while( i < n ){
5 i = i * 2;
6 }
7 }
8}
时间复杂度比较
O(1) < O(log2n) < O(n) < O(nlog2n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
快速掌握算法时间复杂度与空间复杂度
前言
一个算法的优劣好坏,会决定一个程序运行的时间、空间。也许当小数据量的时候,这种影响并不明显,但是当有巨量数据的时候,算法的好坏带来的性能差异就会出天差地别。可以说直接影响了一个产品的高度和广度。每个程序员都想用最优的算法解决问题,我们期待自己写出的代码是简洁、高效的。但是如何评判一个算法的好坏呢?时间复杂度和空间复杂度就是一个很好的标准。
1. 时间复杂度
1.1 概念
执行算法所需要的计算工作量就是我们常说的时间复杂度。该值不一定等于接下来要介绍的基本执行次数。是一个大约的数值,具有统计意义。
1.2 基本执行次数T(n)
根据计算,得出的该算法在输入数据量为n时的,实际执行次数。该值为准确的,具体的数值,有数学意义。
1.3 时间复杂度
根据基本执行次数,去除系数、常数项等得到的渐进时间复杂度。用大O表示法。也就是说,随着数据量的剧增,不同常数项和系数,已经大致不能够影响该算法的基本执行次数。常数项和系数对于计算时间复杂度无意义
1.4 举例说明
T(n) = 2: 该函数总共执行两条语句,所以基本执行次数为2;时间复杂度为O(1): 该函数的基本执行次数只有常数项,所以时间复杂度为O(1)
void test(int n)
{
int a;
a = 10;
}T(n) = 2n: 该函数共循环n次,每次执行2条语句,所以基本执行次数为2n。时间复杂度舍弃系数,为O(n)
void test(int n)
{
int cnt;
for (cnt = 0; cnt < n; cnt++) {
int a;
a= 10;
}
}T(n) = 2 * (1 + 2 + 3 + 4 + ... + n) + 1 = 2 * (1 + n) * n / 2 + 1 = n^2 + n + 1。因为共执行(1 + 2 + 3 + 4 + ... + n) 次循环,每次循环执行2条语句,所有循环结束后,最后又执行了1条语句,所以执行次数如上;时间复杂度为O(n^2),因为n和常数项1忽略,它们在数据量剧增的时候,对于执行次数曲线几乎没有影响了
void test(int n)
{
int cnt1, cnt2;
for (cnt1 = 0; cnt1 < n; cnt1++) {
for (cnt2 = cnt1; cnt2 < n; cnt2++) {
int a;
a = 10;
}
}
a = 11;
}T(n) = 2 * logn 因为每次循环执行2条语句,共执行logn次循环;时间复杂度为O(logn),忽略掉系数2
void test(int n)
{
int cnt;
for (cnt = 1; cnt < n; cnt *= 2) {
int a;
a = 10;
}
}T(n) = n * logn * 2 因为每次循环2条语句,共执行n * logn次循环;时间复杂度为O(nlogn),忽略掉系数2
void test(int n)
{
int cnt1, cnt2;
for (cnt1 = 0; cnt1 < n; cnt1++) {
for (cnt2 = 1; cnt2 < n; cnt2 *= 2) {
int a;
a = 10;
}
}
}T(n) = 2 * n^3 因为每次循环2条语句,共执行n^3 次循环;时间复杂度为O(n^3),忽略掉系数2
void test(int n)
{
int cnt1, cnt2, cnt3;
for (cnt1 = 0; cnt1 < n; cnt1++) {
for (cnt2 = 0; cnt2 < n; cnt2++) {
for (cnt3 = 0; cnt3 < n; cnt3++) {
int a;
a = 10;
}
}
}
}斐波那契数列的递归实现,每次调用该函数都会分解,然后要再调用2次该函数。所以时间复杂度为O(2^n)
int test(int n)
{
if (n == 0 || n == 1) {
return 1;
}
return (test(n-1) + test(n-2));
}1.5 时间复杂度比较
O(1) < O(log2n) < O(n) < O(nlog2n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
2. 空间复杂度
2.1 概念
一个算法所占用的存储空间主要包括:
程序本身所占用的空间
输入输出变量所占用的空间
动态分配的临时空间,通常指辅助变量
输入数据所占空间只取决于问题本身,和算法无关。我们所说的空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度,即第三项。通常来说,只要算法不涉及到动态分配的空间以及递归、栈所需的空间,空间复杂度通常为0(1)。
2.2 举例说明
S(n) = O(1).空间复杂度为O(1),因为只有a, b, c, cnt四个临时变量。且临时变量个数和输入数据规模无关。
int test(int n)
{
int a, b, c;
int cnt;
for (cnt = 0; cnt < n; cnt++) {
a += cnt;
b += a;
c += b;
}
}S(n) = O(n).空间复杂度为O(n),因为每次递归都会创建一个新的临时变量a。且共递归n次。
int test(int n)
{
int a = 1;
if (n == 0) {
return 1;
}
n -= a;
return test(n);
}3. 函数的渐进增长与渐进时间复杂度
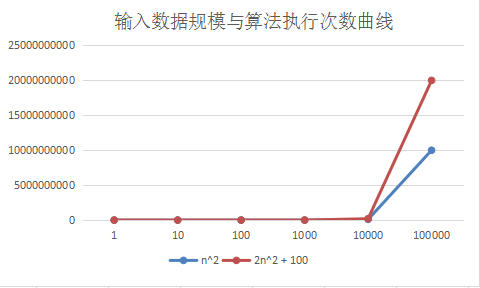
在上面的例子中,我们通常都会舍弃掉系数和常数项。这是因为当输入量剧增,接近正无穷时,系数和常数项已经不能够影响执行次数曲线。不同的系数和常数项曲线会完全重合。我做了一个折线图用来比较当输入值n激增时,n^2 曲线和 2n^2 + 100 曲线。可以看到,当数据量剧增时,系数和常数项对于统计时间复杂度都不再有意义,两条曲线几乎完全重合。
4. 不同算法的时间复杂度 & 空间复杂度
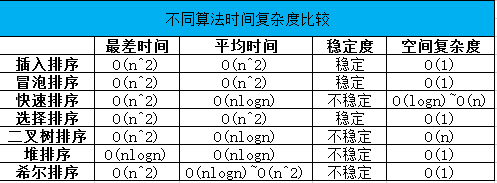
下图是我做的一个表格,整理了不同的排序算法的时间复杂度和空间复杂度供大家参考:
感谢大家的阅读,大家喜欢的请帮忙点下推荐。后面会继续出精彩的内容,敬请期待!
如果说数学是皇冠上的一颗明珠,那么算法就是这颗明珠上的光芒。算法让这颗明珠更加熠熠生辉,为科技进步和社会发展照亮前进的路。数学是美学,算法是艺术。走进算法的人,才能体会它的魅力。
打开算法之门
瑞士著名的科学家N.Wirth教授曾提出:数据结构+算法=程序。
数据结构是程序的骨架,算法是程序的灵魂。
其实在我们的生活中,算法无处不在。我们每天早上起来,刷牙、洗脸、吃早餐,都在算着时间,以免上班或上课迟到;去超市购物,在资金有限的情况下,考虑先买什么、后买什么,算算是否超额;在家中做饭,用什么食材、调料,做法、步骤,还要品尝一下咸淡,看看是否做熟。所以,不要说你不懂算法,其实你每天都在用。
妙不可言——算法复杂性
我们首先看一道某公司的招聘试题。
写一个算法,求下面序列之和:

当你看到这个题目时,你会怎么想?for语句?while循环?
先看算法1-1:
//算法1-1
sum=0;
for(i=1;i<=n;i++)
{
sum=sum+pow(-1,i) //pow(-1,i)表示-1的i次幂
}这段代码可以实现求和运算,但是为什么不这样算呢?
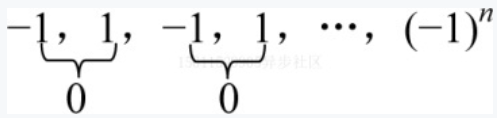
再看算法1-2:
//算法1-2 if(n%2==0) //判断n是不是偶数,%表示求余数 sum=0; else sum=-1;
有的人看到这个代码后恍然大悟,原来可以这样啊!这不就是数学家高斯使用的算法吗?
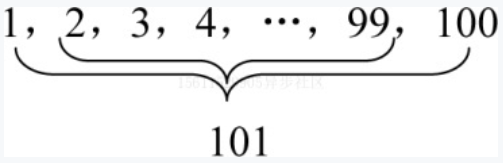
一共50对数,每对之和均为101,那么总和为:
(1+100)*50=5050
1787年,10岁的高斯用了很短的时间算出了结果,而其他孩子却要算很长时间。
可以看出,算法1-1需要运行n+1次,如果n=10000,就要运行10001次,而算法1-2仅仅需要运行1次!是不是有差别很大?!
问:高斯的方法我也知道,但遇到类似的题还是……我用的笨办法是算法吗?
答:是算法。
【算法】是指对特定问题求解步骤的一种描述。
算法只是对问题求解方法的一种描述,它不依赖于任何一种语言,既可以用自然语言、程序设计语言(C、C++、Java、Python等)描述,也可以用流程图、框图来表示。一般为了更清楚地说明算法的本质,我们去除了计算机语言的语法规则和细节,采用“伪代码”来描述算法。
“伪代码”介于自然语言和程序设计语言之间,它更符合人们的表达方式,容易理解,但不是严格的程序设计语言,如果要上机调试,需要转换成标准的计算机程序设计语言才能运行。
算法有哪些特性呢?
(1)有穷性:算法是由若干条指令组成的有穷序列,总是在执行若干次后结束,不可能永不停止。
(2)确定性:每条语句有确定的含义,无歧义。
(3)可行性:算法在当前环境条件下可以通过有限次运算实现。
(4)输入输出:有零个或多个输入,一个或多个输出。
问:算法1-2的确算得挺快的,但如何知道我写的算法好不好呢?
"好"算法的标准
(1)正确性:正确性是指算法能够满足具体问题的需求,程序运行正常,无语法错误,能够通过典型的软件测试,达到预期的需求。
(2)易读性:算法遵循标识符命名规则,简洁易懂,注释语句恰当适量,方便自己和他人阅读,便于后期调试和修改。
(3)健壮性:算法对非法数据及操作有较好的反应和处理。例如,在学生信息管理系统中登记学生年龄时,若将21岁误输入为210岁,系统应该提示出错。
(4)高效性:高效性是指算法运行效率高,即算法运行所消耗的时间短。算法时间复杂度就是算法运行需要的时间。现代计算机一秒钟能计算数亿次,因此不能用秒来具体计算算法消耗的时间,由于相同配置的计算机进行一次基本运算的时间是一定的,我们可以用算法基本运算的执行次数来衡量算法的效率。因此,将算法基本运算的执行次数作为时间复杂度的衡量标准。
(5)低存储性:低存储性是指算法所需要的存储空间低。对于像手机、平板电脑这样的嵌入式设备,算法如果占用空间过大,则无法运行。算法占用的空间大小称为空间的复杂度。
除了(1)~(3)中的基本标准外,我们对好的算法的评判标准就是高效率、低存储。
问:(1)~(3)中的标准都好办,但时间复杂度怎么算呢?
【时间复杂度】:算法运行需要的时间,一般将算法的执行次数作为时间复杂度的度量标准。
看算法1-3,并分析算法的时间复杂度。
//算法1-3
sum=0; //运行1次
total=0; //运行1次
for(i=1;i<=n;i++) //运行n+1次
{
sum=sum+i; //运行n次
for(j=1;j<=n;j++) //运行n*(n+1)次
total=total+i*j; //运行n*n次
}把算法的所有语句的运行次数加起来:1+1+n+1+n+n*(n+1)+n*n,可以用一个函数T(n)表达:
当n足够大时,我们可以看到算法运行时间主要取决于第一项,后面的甚至可以忽略不计。
用极限表示为:
,C为不等于0的常数
如果用时间复杂度的渐近上界表示,如图1-1所示。
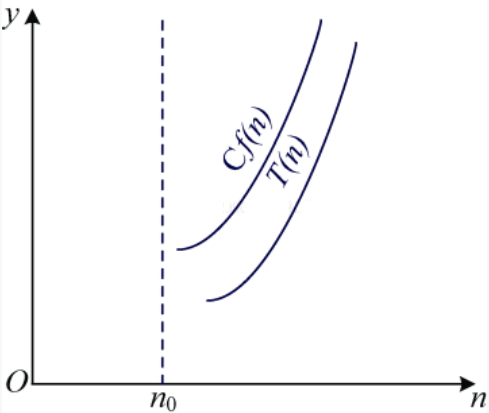
从图1-1中可以看出,当 时,
,当n足够大时,T(n)和f(n)近似相等。因此,我们用
来表示时间复杂度渐近上界,通常用这种表示法衡量算法时间复杂度。算法1-3的时间复杂度渐近上界为
,用极限表示为:
还有渐近下界符号 ,如图1-2所示。
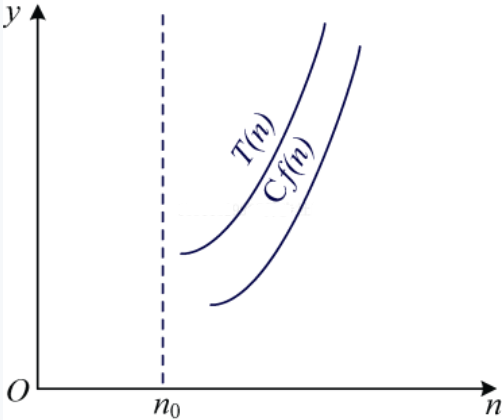
从图1-2可以看出,当 时,
,当n足够大时,T(n)和f(n)近似相等,因此,我们用
来表示时间复杂度接近下界。
渐近精确界符号 ,如图1-3所示。

从图1-3中可以看出,当 时,
,当n足够大时,T(n)和f(n)近似相等。这种两边逼近的方式,更加精确近似,因此,用
来表示时间复杂度渐近精确界。
不过,我们通常使用时间复杂度接近上界 来表示时间复杂度。
在算法分析中,渐近复杂度是对算法运行次数的粗略估计,大致反映问题规模增长趋势,而不必精确计算算法的运行时间。
在计算渐近时间复杂度时,可以只考虑对算法运行时间贡献大的语句,而忽略那些运算次数少的语句,循环语句中处在循环内层的语句往往运行次数最多,即为对运行时间贡献最大的语句。例如在算法1-3中,total=total+i*j是对算法贡献最大的语句,只计算该语句的运行次数即可。
注意:不是每个算法都能直接计算运行次数。
例如算法1-5中,在a[n]数组中顺序查找x,返回其下标i,如果没找到,则返回-1。

我们很难计算算法1-5中的程序到底执行了多少次,因为运行次数依赖于x在数组中的位置,如果第一个元素就是x,则执行1次(最好情况);如果最后一个元素是x,则执行n次(最坏情况);如果分布概率均等,则平均执行次数为(n+1)/2。
有些算法,如排序、查找、插入等算法,可以分为最好、最坏和平均情况分别求算法渐近复杂度,但我们考察一个算法通常考察最坏的情况,而不是考察最好的情况,最坏情况对衡量算法的好坏具有实际的意义。
【空间复杂度】是算法占用的空间大小。一般将算法的辅助空间作为衡量空间复杂度的标准。
空间复杂度的本意是指算法在运行过程中占用了多少存储空间。算法占用的存储空间包括:
输入/输出数据;
算法本身;
额外需要的辅助空间。
输入/输出数据占用的空间是必需的,算法本身占用的空间可以通过精简算法来缩减,但这个压缩的量是很小的,可以忽略不计。而在运行时使用的辅助变量所占用的空间,即辅助空间是衡量空间复杂度的关键因素。
=======================================
=======================================


