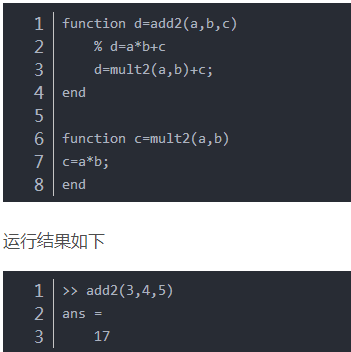
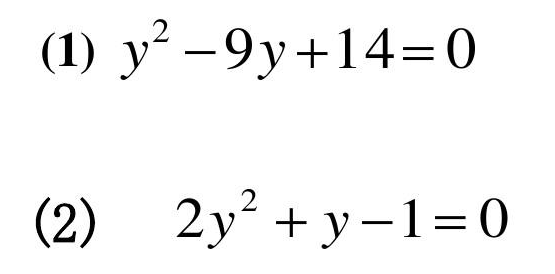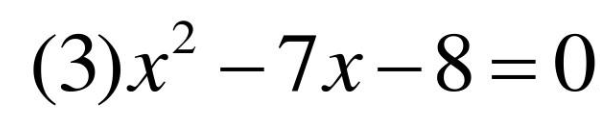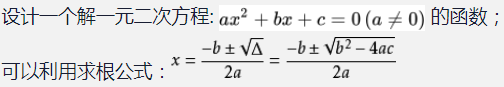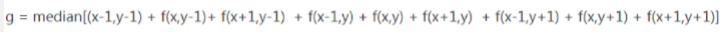MATLAB函数
MATLAB 程序,大致分为两类:M 脚本文件 (M-Script) 和 M 函数 (M-function) , 它们均是普通的 ASCII 码构成的文件。
脚本和函数都允许您通过将命令序列存储在程序文件中来重用它们。函数提供的灵活性更大,主要因为您可以传递输入值并返回输出值。此外,函数能够避免在基础工作区中存储临时变量,并且运行速度比脚本更快。
脚本与函数区别: 例:脚本 在名为 triarea.m 的文件中创建一个脚本以计算三角形的面积:
b = 5; 保存文件后,您可以从命令行中调用该脚本:
triarea a =
例:函数
function a = triarea (b,h) 保存该文件后,您可以从命令行调用具有不同的基值和高度值的函数,不用修改脚本:
a1 = triarea(1,5) a1 =
1.M 函数
一个函数是一组在一起执行任务的语句。 在MATLAB中,函数在单独的文件中定义。文件的名称和函数的名称应该是一样的。函数在自己的工作空间内的变量上运行,这个变量也称为本地工作空间,与在MATLAB命令提示符下访问的工作区(称为基本工作区)不同。
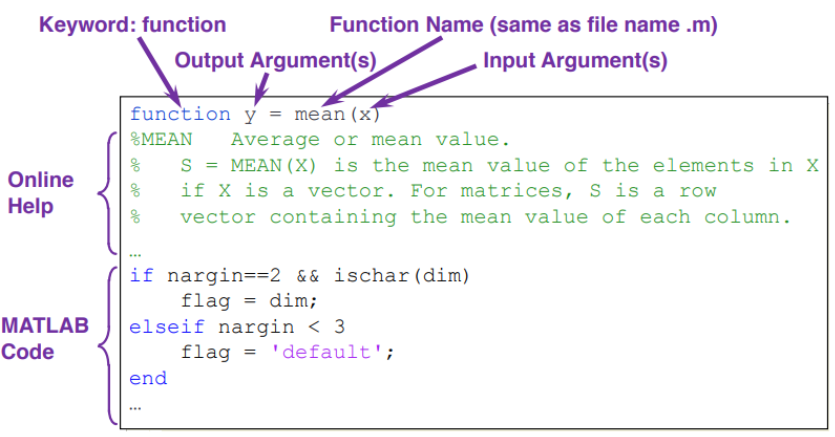
MATLAB 的 M 函数是由 function 语句引导的,函数可以接受多个输入参数,并可能 也可以不返回输出参数) 。
其基本格式:function [返回变量列表] = 函数名 (输入变量列表)
function out1,out2 ..., outN ] = myfun (in1,in2,in3, ...,inN )%函数使用说明 end 可以将
保存在以下位置:
(1)只包含函数定义的函数文件中。文件的名称须与文件中第一个函数的名称一致。
(2)包含命令和函数定义的脚本文件中。函数必须位于该文件的末尾。脚本文件不能与文件中的
函数具有相同的名称。R2016b 或更高版本的脚本中支持函数。
关于
为提高可读性,可使用 end 关键字来表示文件中每个函数的末尾,以下情况下需要 end 关键字:
文件中有任意函数包含嵌套函数。
该函数是函数文件中的局部函数,并且文件中有局部函数使用end关键字。
该函数是脚本文件内的局部函数。
示例: 建立一个函数计算圆的周长和面积
第1步:建立函数
第2步:函数的调用
练习1: 建立一个名为sjxjs的函数,计算三角形的周长和面积.
调用方法为: [S,L]=sjxjs(inputArg1,inputArg2,inputArg3)
其中 inputArg1,inputArg2,inputArg3为三角形的三个边长,返回的参数S,L为三角形的面积和周长。
function [S,L] = sjxjs(a,b,c)
% sjxjs()函数的作用是计算三角形面积与周长,
% 输入参数inputArg1,inputArg2,inputArg3分别是三个边长
% 输出参数S和L为三角形的面积和周长
if (a+b)>c&(a+c)>b&(b+c)>a
fprintf('这是一个合理的三角形\n')
p=(a+b+c)/2;
L=(a+b+c);
S=sqrt(p*(p-a)*(p-b)*(p-c));
fprintf('这个三角形周长为:%.3f , 面积为:%.3f \n',L,S)
else
fprintf('输入的三个边长构不成三角形,请重新输入 \n')
end
end
练习2 设计一个专门用于生成n*m的希尔伯特矩阵的函数:myxebt() 创建名为myxebt.m的函数文件,从左上角菜单中点击新建->函数,
并在其中键入以下代码
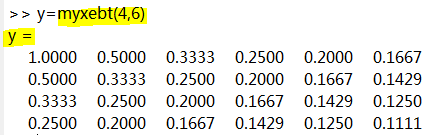
function H= myxebt(x1,x2) %本函数用于创建n行m列的希尔伯特矩阵。 for n=1:x1 end 函数语句之后的注释行提供了帮助文本(函数的说明书 )。
当键入 help myxebt 时,这些信息被打印
现在,我们来使用这个函数 -
练习3: 制作一个名为 yyecfc()的函数,用来解一元二次方程的两个根 x1,x2,其调用格式为: [x1,x2] = yyecfc(a,b,c)
并调用这个函数来解以下几个方程。
function [x1,x2] = yyecfc(a,b,c)
%这个函数用来计算一元二次方程的根
% a,b,c为一元二次方程的系数,x1,x2为根
x1 = (-b+sqrt(b^2-4*a*c))/(2*a);
x2 = (-b-sqrt(b^2-4*a*c))/(2*a);
end
练习4
如,设计一个清屏、关闭各种窗口的小函数,命名为ccc.m然后保存在工作路径下,之后在matlab命令行窗口之间输入:ccc,然后回车,就可以执行清屏...
function ccc() clc
问:Matlab的function写完后,最后加不加end?
答: 加不加都可以。最好加就统一加,不加就都不加。
如果你的函数内还嵌套有子函数,或者顺序的写了别的调用的子函数,此时最后要加end
https://www.ilovematlab.cn/thread-60628-1-1.html
主函数和子函数 每个函数文件包含主要出现的必需的主函数,以及主函数之后的任意数量的可选子函数。
在Matlab中,可以把多个函数的定义放在一个函数文件中,这些函数中, 第一个出现的为主函数,其他的函数均为子函数,需要注意的是,子函数只能被同一个函数文件中的函数调用。在保存函数文件的时候,函数文件名一般保持和主函数名相同,且外部程序只能对主函数进行调用。
可以从命令行或其他函数的文件外部调用主函数,但不能从命令行或函数文件外的其他函数调用子函数。
子函数仅对函数文件中的主函数和其他子函数可见。
例1:采用子函数方式,制作一个成绩查询程序
function chengji(x1,x2) %主函数相当于工程总负责人
%chengji(x1,x2) 中,第一个参数x1为平时成绩,第二个参数x2为期末成绩
%用三个子函数,分别实现:分数检测、总分的计算、输出
[X_ps,X_qm]= jiance (x1,x2);
S_zf= jisuanzf (X_ps,X_qm);
shuchu (X_ps , X_qm , S_zf);
end
function [X_ps,X_qm]= jiance (x1,x2) %各个子函数就是职能不同的分包商
%子函数1,专业负责检查输入是否有错
X_ps=x1;
X_qm=x2;
while X_ps>100 | X_ps<0 | X_qm>100 | X_qm<0
fprintf('输入有误,输入的分数应该在0-100之间 \n');
X_ps=input('请重新输入你的 , 平时分:');
X_qm=input('请重新输入你的 , 期末考试分:');
end
end
function S_zf= jisuanzf (x1,x2)
%子函数2,专业负责计算总分
X_ps=x1;
X_qm=x2;
S_zf=0.4*X_ps+0.6*100*(X_qm/100)^0.5;
end
function shuchu (x1,x2,x3)
%子函数3,专业负责打印输出
X_ps=x1;
X_qm=x2;
S_zf=x3;
if S_zf>=90
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩优秀. \n' ,X_ps ,X_qm , S_zf);
elseif S_zf>=70&S_zf<90
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩良好. \n',X_ps ,X_qm , S_zf);
elseif S_zf>=60&S_zf<70
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩及格. \n',X_ps ,X_qm , S_zf);
elseif S_zf<60
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 等着补考吧.. \n',X_ps ,X_qm , S_zf);
end
end
例2 下面编写一个名为quadratic的函数来计算二次方程的根。该函数需要三个输入参数:二次系数,线性系数和常数项,计算并会返回根。
函数文件 quadratic包含主函数quadratic和次函数和子函数disc(它用于计算判别式)。
function [x1,x2] = quadratic (a,b,c) %主函数 %this function returns the roots of a quadratic equation. d disc end dis disc (a,b,c) %子函数 ,用于计算判别式。 %sub-function : calculates the discriminant - 4*a*c);
可以从命令提示符调用上述函数
>> quadratic(2,4,-4)
练习: 设计一个名为mymax( )的函数,调用格式为 y=mymax(A ),输出y为输入矩阵A的最大值。
function m=mymax(A)
[row,col]=size(A); %测量矩阵A的行数和列数
m=-Inf; %初始化最大值m, 也可以写为 m=A(1,1);
for k1=1:row %遍历行
for k2=1:col %遍历列
if A(k1,k2)>=m %如果当前元素大于m
m=A(k1,k2); %则把m更新为当前元素
end
end
end
end
%如果要求不但返回最大值,而且还要返回最大值所在的行数和列数
function [m,x,y]=mymax(A)
[row,col]=size(A); %测量矩阵A的行数和列数
m=A(1,1); %初始化最大值m为A中的第1行第1列的元素;
x=1; %初始化最大值m对应的行x的值为第1行
y=1; %初始化最大值m对应的列y的值为第1列
for k1=1:row %遍历行
for k2=1:col %遍历列
if A(k1,k2)>=m %如果当前元素大于m
m=A(k1,k2); %则把m更新为当前元素
x=k1; %则把x更新为当前元素对应的行数k1
y=k2; %则把y更新为当前元素对应的列数k2
end
end
end
end
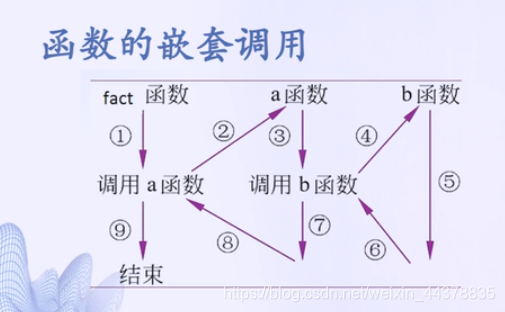
3.嵌套函数
嵌套函数 可以在一个函数的主体内定义另一个函数。这样的函数被称为嵌套函数。嵌套函数包含任何其他函数的部分或全部组件。
function chengji(x1,x2)
%chengji(x1,x2) 中,第一个参数x1为平时成绩,第二个参数x2为期末成绩
[X_ps,X_qm]=jiance(x1,x2);
S_zf=jisuanzf(X_ps,X_qm);
shuchu(X_ps , X_qm , S_zf);
function [X_ps,X_qm]=jiance(x1,x2) %各个子函数就是职能不同的分包商
%内部子函数1,专业负责检查输入是否有错
X_ps=x1;
X_qm=x2;
while X_ps>100 | X_ps<0 | X_qm>100 | X_qm<0
fprintf( '输入有误,输入的分数应该在0-100之间 \n' );
X_ps=input( '请重新输入你的 , 平时分:' );
X_qm=input( '请重新输入你的 , 期末考试分:' );
end
end
function S_zf=jisuanzf(x1,x2)
%内部子函数2,专业负责计算总分
X_ps=x1;
X_qm=x2;
S_zf=0.4*X_ps+0.6*100*(X_qm/100)^0.5;
end
function shuchu(x1,x2,x3)
%内部子函数3,专业负责打印输出
X_ps=x1;
X_qm=x2;
S_zf=x3;
if S_zf>=90
fprintf( '您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩优秀. \n' ,X_ps ,X_qm , S_zf);
elseif S_zf>=70&S_zf<90
fprintf( '您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩良好. \n' ,X_ps ,X_qm , S_zf);
elseif S_zf>=60&S_zf<70
fprintf( '您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩及格. \n' ,X_ps ,X_qm , S_zf);
elseif S_zf<60
fprintf( '您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 等着补考吧.. \n' ,X_ps ,X_qm , S_zf);
end
end
end
4、matlab函数中的形参与实参 学过其他编程语言的同学在对待函数时,往往需要急切地弄清楚什么时候函数传递形参,什么时候传递实参呢?
先上结论:MATLAB函数永远传递形参!
没有理解的同学可以通过下面的例子感受一下。
假设我现在有一个1*5的矩阵,我现在想让这个矩阵的第一个元素加1,那么有什么办法呢?最直观的想法是这样的:
%%% 文件add_one.m %%% 表面上看来,这个函数对于任何传递进来的矩阵mat,都将第一个元素进行了加1操作。我们对其进行一下测试:
%%% 文件Script5_3.m %%% 我们惊讶地发现,mat的值并没有发生任何变化!事实上,无论我们在函数内对传入参数进行什么操作,都不会影响到参数在主程序中的原本值,这是因为MATLAB使用的是“形参传递”。在这个过程中,实际上在MATLAB内部发生了如下的事情:
1 主程序调用函数,此时需要传递参数mat=[1,2,3,4,5] 因此,无论我们怎么做,主程序中的值都无法在函数中进行修改。那我们怎样实现上述需求呢?一种方式是可以将mat_copy的值直接返回给主程序,主程序再将mat的值替换为函数返回值。如下:
%%% 文件add_one.m %%% 这样做或许显得不美观,但也不失为一种好方法。
还有一种方法则是利用 全局变量 的方法。
5. 全局变量
全局变量
在介绍全局变量之前,我们需要先了解一下变量空间。变量空间是指MATLAB计算过程中当前状态可以使用的所有变量。 function) 运行过程中就无法使用主程序定义的变量,因此我们说它们属于不同的变量空间。
一般而言,MATLAB的变量空间可以有多个 ,其中所有的脚本m文件共享一个变量空间,例如先执行Script2_1.m,再执行Script2_2.m时仍然可以访问在之前的脚本中已经定义的函数;而不同的函数 (function) 文件属于不同的变量空间,且不同于脚本m文件的变量空间,
因此任何函数都不能调用在其他函数中或者主程序中定义的变量。
之所以传递到函数中的参数不能修改,是因为主程序中传进去的参数是属于主程序的变量空间,当函数开始执行时,主程序的变量就被暂存起来无法改动了。那我们自然想到,能不能利用什么方法,使得一个变量不只是属于主程序呢?答案就是全局变量。
全局变量不属于任何一个程序模块,在任何时候都可以被修改。
我们使用如下的方式定义或使用一个全局变量:
global GLOBAL_VAR; %建议全局变量的名称使用大写字母,以区别于其他变量。
注意:使用全局变量前,要先进行声明,以告知编译器:这是一个全局变量,请不要在局部变量里面寻找。
例1:
x=1:10;
global exponential %先 声明全局变量exponential(指数)
exponential =2; %再 设置全局变量的值,后边function里面的这个变量会跟着同步取值
y=Exponentiation(x) %调用Exponentiation函数
function y = Exponentiation(x) %定义一个名为Exponentiation(幂运算)的函数
global exponential %声明全局变量exponential(指数)
y = x.^ exponential ; %对输入的x进行操作,幂指数由全局变量给定。
end
使用全局变量非常方便,但是需要注意的是,使用全局变量与函数化、模块化的概念完全相悖,大量使用全局变量将使得程序的逻辑控制变得复杂,可读性变差。因此建议大家尽量不要使用全局变量,以免生出“一个月前写的程序自己都看不懂”的悲剧。
如,上例完全可以不用全局变量,改为:
6 .return语句
return 强制 MATLAB在到达调用脚本或函数的末尾前将控制权交还给调用程序。
return
注意:在条件块(例如 if 或 switch)或循环控制语句(例如 for 或 while)使用 return 时需要小心。当 MATLAB 到达 return 语句时,它并不仅是退出循环,还退出脚本或函数,并将控制权交还给调用程序或命令提示符。
function d = det(A)return
当然, 普通的脚本里(非 function )也可以用,如使用多重for循环来搜索某个答案的时候,如果希望搜索到 一个 答案就跳出 所有循环 ,就可以采用:
for ...
for...
for...
if 符合某某条件
return
end
7.1 匿名函数
提起函数式编程,就不得不提到大名鼎鼎的Lambda函数
首先回想我们使用函数的流程。我们需要确定函数的输入与输出、函数名,新建函数m文件,编写函数体,然后在主程序中对函数进行调用。但很多时候,我们编写的函数可能往往只有一行或更少,这种情况下单独编写一个函数m文件就显得非常麻烦。甚至有些时候,这个函数我们只需要用一次,能不能不取名呢?匿名函数(Lambda函数)就很好地解决了这个问题。
匿名函数的声明如下:
fhandle=@(arglist) expression 其中 fhandle 就是调用该函数的函数句柄(function handle), 函数指针 , arglist是参数列表 ,多个参数使用逗号 Expression则是该函数的表达式
匿名函数的形式十分简洁,将整个函数的定义缩减到一行内。
例: % 定义add函数的Lambda形式
lambda_add = @(a, b)a + b 例:
在这个例子中,编写一个名为power的匿名函数,它将使用两个数字作为输入,并将第一个数字返回到第二个数字的幂值。
创建脚本文件并在其中键入以下代码
power = @(x, n) x.^n; result1 = power (7, 3) power (49, 0.5) power (10, -10) power (4.5, 1.5)
当运行该文件,得到以下结果
result1 = 343
匿名函数可以使用工作空间的变量,例如创建函数f(x,y)=x^2+y^3:
>> p=2;
>> q=3;
>> f =@(x,y) x^p+y^q
f =
@(x,y)x^p+y^q
计算f(2,3):
>> f (2,3)
ans =
31
如果修改p或者q的值,例如将q改为2:
q =
2
>> f(2,3)
ans =
31
计算结果并没有改变,这是因为,该函数句柄保存的是函数在创建时的快照,而不是动态的访问其中的变量,如果希望获取新值,需要重新创建一次该函数,完整的方法应该是这样的:
>> q=2;
>> f =@(x,y) x^p+y^q
f =
@(x,y)x^p+y^q
>> f (2,3)
ans =
13
匿名函数应用实例:
%例1
fun1= @(x) x.^2;
fun2= @(x) [x.^0.5 , x.^2 , sin(x) ]; %可以同时写多个函数,水平排列
fun3= @(x) [x.^0.5 ; x.^2 ; sin(x) ]; %可以同时写多个函数,垂直排列
a1=fun1(2) %调用函数
a2=fun2(2)
a3=fun3(2)
q1=fun1( [2:4] ) %用数组作为参数调用函数
q2=fun2( [2:4] )
q3=fun3( [2:4] )
%例2
x=[0:0.001:6];
f1 = @(x) sin(80*x).*exp(-x);
y= f1 (x);
plot(x,y)
练习:使用 Lambda函数来解一元二次方程。
yyec=@(a,b,c)[(-b+sqrt(b^2-4*a*c))/(2*a),(-b-sqrt(b^2-4*a*c))/(2*a)];
ans1=yyec(1,2,-7)
ans2=yyec(3,-12,8)
ans3=yyec(-2,0,9)
匿名函数的表达式中也可以有参数的传递,比如:
>> a=1:5;
>> b=5:-1:1;
>> c=0.1:0.1:0.5;
>> f=@(x,y)x.^2+y.^2+c;
>> f(a,b)
ans = 26.1000 20.2000 18.3000 20.4000 26.5000
c作为表达式中的参数,进行了数据传递。
上面都是单重匿名函数,也可以构造 多重匿名函数 ,如:
>> f=@(x,y)@(a) x^2+y^+a;
>> f1=f(2,3)
f1 = @(a)x^2+y^+a
>> f2=f1(4)
f2 = 85
每个@后的参数从它后面开始起作用,一直到表达式的最后。
1、A handle is a pointer to function(句柄是指向函数的指针 )
2、Can be used to pass functions to other functions(句柄是指向函数的指针,可用于将函数传递给其他函数)
示例代码:
function [y] = xy_plot %xy_plot receives the handle of a function and plots that xy_plot @sin
内联函数
内联(inline)函数是MATLAB 7以前经常使用的一种构造函数对象的方法。在命令窗口、程序或函数中创建局部函数时,通过使用inline构造函数,而不用将其储存为一个M文件,同时又可以像使用一般函数那样调用它。
MATLAB中的内联函数借鉴了C语言中的内联函数,在C语言中,内联函数是通过编译器控制来实现的,它只在需要用到的时候,内联函数像宏一样的展开,所以取消了函数的参数压栈,减少了调用的时间和空间开销。在MATLAB中也有类似的性质。由于内联函数是储存于内存中而不是在M文件中,省去了文件访问的时间,加快了程序的运行效率。
虽然内联函数有M文件不具备的一些优势,但是由于内联函数的使用,也会受到一些制约。首先,不能在内联函数中调用另一个inline函数;另外,只能由一个MATLAB表达式组成,并且只能返回一个变量。是要注意 内联函数这种函数比较多的时候会占用比较多的内存空间。
创建一个内联函数非常简单,就是使用inline方法,例如:
>> f=inline('t^2-3*t-4')
f =
Inline function:
f(t) = t^2-3*t-4
MATLAB会通过检查字符串来推断自变量,例如上面的函数中t就是自变量,如果没有找到,将会使用x作为缺省的自变量,例如常数函数:
>> g=inline('3')
g =
Inline function:
g(x) = 3
另外,对于inline也支持多元函数:
>> h=inline('x+y')
总结:匿名函数的作用(好处) :匿名函数的作用:主要实现自己定义matlab中的函数,从而扩大函数的使用功能。
函数简介:匿名函数不以文件形式驻留在文件夹上
和内联函数(inline)相比,匿名函数的优越性在于可以直接使用workspace中的变量,不必申明,非常适合嵌入到M文件中 。
匿名函数的补充知识: (1)函数句柄的概念 https://ww2.mathworks.cn/help/matlab/function-handles.html 可用于间接调用函数的变量
函数句柄是一种表示函数的 MATLAB 数据类型。函数句柄的典型用法是将一个函数传递给另一个函数。例如,您可以将函数句柄用作基于某个值范围计算数学表达式的函数的输入参数。
函数句柄可以表示命名函数或匿名函数。要创建函数句柄,请使用 @ 运算符。例如,创建用于计算表达式 x2 – y2 的匿名函数的句柄:
f = @(x,y) (x.^2 - y.^2); 有关详细信息,请参阅创建函数句柄 。
函数
(2)Matlab中函数句柄@的作用及介绍
问:f=@(x)acos(x)表示什么意思?其中@代表什么?
答:表示f为函数句柄,@是定义句柄的运算符。f=@(x)acos(x) 相当于建立了一个函数文件:
% f.m
function y=f(x)
y=acos(x);
若有下列语句:xsqual=@(x)1/2.*(x==-1/2)+1.*(x>-1/28&x<1/2)+1.2.*(x==-1/2);
则相当于建立了一个函数文件:
% xsqual.m
function y=xsqual(x)
y=1/2.*(x==-1/2)+1.*(x>-1/28&x<1/2)+1.2.*(x==-1/2);
详细说明:
1、函数句柄/function_handle(@):是一种间接调用函数的方式。
2、语法:handle=@functionname or handle=@(arglist)anonymous_function
3、描述:函数句柄(function handle)是一种能够提供函数间接调用的matlab value。你可以通过传递句柄来调用各种其他功能。你也可以将句柄存储到数据结构中备用(例如Handle Graphic 回调)。句柄是matlab的标准数据类型之一。
当创建句柄时,你所指定的函数必须在matlab搜索路径之中,并且必须在创建语句的scope之中。例如,只要在定义子函数的文件之中,你句可以为这个子函数创建句柄。这些条件不适用于evaluate函数句柄。例如,你可以在一个单独(out-scope)通过句柄执行一个子函数,这要求句柄是在in-scope创建的。
handle=@(arglist)anonymous_function用来创建匿名函数(anonymous function)并返回该匿名函数的句柄。括号右边的函数体是单个的matlab语句(statement)或者matlab命令。arglist是一个用逗号“,”分隔的输入变量列表。该函数通过句柄handle执行。
备注:函数句柄是标准的matlab数据类型。因此,你可以像matlab其他数据类型一样进行操作。
4、函数句柄的好处
①提高运行速度。因为matlab对函数的调用每次都是要搜索所有的路径,从set path中我们可以看到,路径是非常的多的,所以如果一个函数在你的程序中需要经常用到的话,使用函数句柄,对你的速度会有提高的。
②使用可以与变量一样方便。比如说,我再这个目录运行后,创建了本目录的一个函数句柄,当我转到其他的目录下的时候,创建的函数句柄还是可以直接调用的,而不需要把那个函数文件拷贝过来。因为你创建的function handles中,已经包含了路径,
1、Lambda 表达式是面向对象平台中 函数式编程原则的实现 。 直接在代码中表达函数 ,而无需面向对象的包装器来支持它们(从语言语法的角度来看)。在方法上,可以看作是匿名方法。 函数式编程语言 中一样, 因此它们获得了可以从不可变的、一致的函数中获得的所有并行性和并发性优势。 可以在任何需要函数式接口的代码中使用 ,这实际上意味着,在内部,lambda 表达式是函数式接口的实现,因此是语言中的一等公民。它们可以被分配/存储,作为参数传递等。
链接:https://www.zhihu.com/question/20125256/answer/2327384711
函数句柄通过 @ 符号创建,语法为:
fhandle = @functionname
其中,functionname 为函数名,fhandle 就是为该函数创建的句柄。 函数句柄也可以通过创建匿名函数的方式创建,语法为:
fhandle = @(arglist)expr
其中,expr 为函数体,arglist 为逗号分隔开的输入变量列表。比如,expr = @(x) x.^2 创建了用于计算输入变量平方的匿名函数。 如果输入变量为空,则 arglist 为空。t = @()datestr(now) 匿名函数的输入变量为空。 可以通过函数句柄实现对函数的间接调用,其调用语法为:
fhandle(arg1, arg2, …, argN) %其中fhandle为函数句柄
可以使用单元数组同时为多个函数创建各自的句柄,
例如,trigFun = {@sin, @cos, @tan},定义了元胞数组 trigFun ,它包含 3 个函数的句柄。 执行 plot(trigFun{2}(-pi:0.01:pi)) ,就是利用句柄调用了第二个函数,即 cos 函数。
————————————————
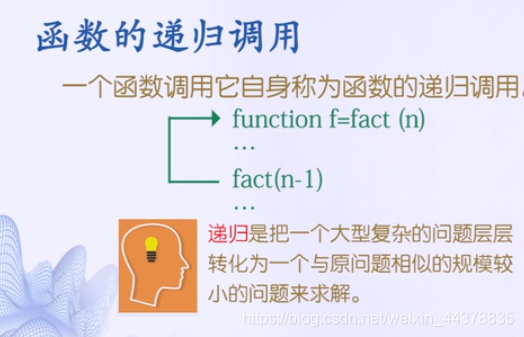
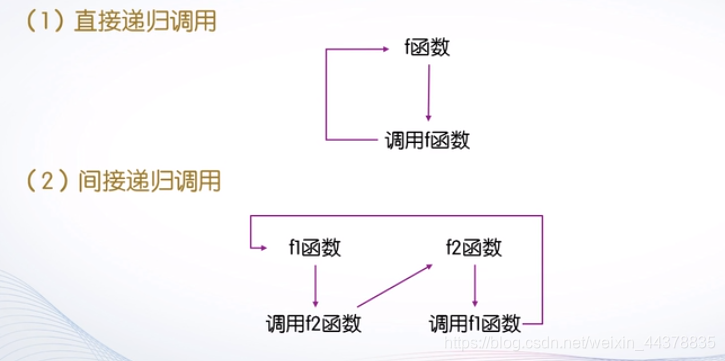
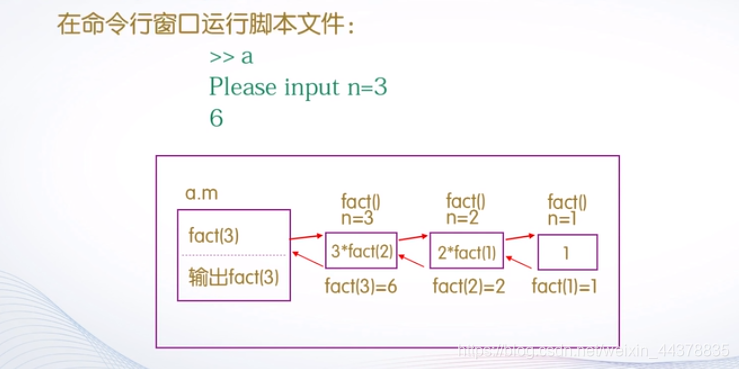
9.函数的递归调用
练习1:利用函数递归调用,解决斐波那契 数列问题
斐波那契数列(Fibonacci sequence),又称 黄金分割 数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“ 兔子数列 ”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、55,89……
斐波那契数列递推定义: F (1)=1, F (2)=1, F (n)= F (n - 1)+ F (n - 2)( n ≥ 3, n ∈ N*)
function F= Fibo (n)
if n==1
F=1;
end
if n==2
F=1;
end
if n>=3
F=Fibo (n-1)+Fibo (n-2);
end
end
%用for循环来实现
n=20;
F=zeros(1,n);
F(1)=1;
F(2)=1;
for k=3:n
F(k)=F(k-1)+F(k-2);
end
F
练习2:汉诺塔问题
汉诺塔(Hanoi Tower),是一种经典的数学问题和递归算法示例。
这个问题最初是由法国数学家爱德华·卢卡斯(Édouard Lucas)在1883年提出的,而“汉诺塔”这个名称则是来源于越南河内的一个传说。
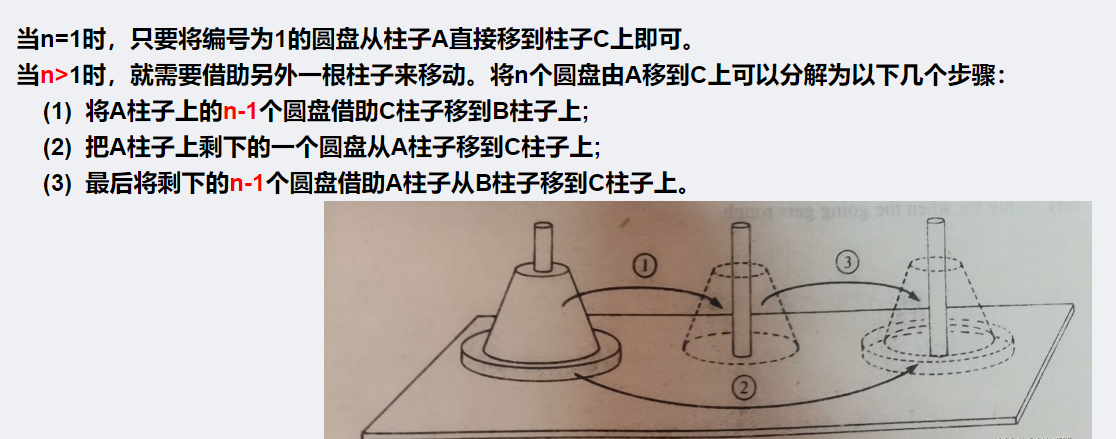
汉诺塔的问题描述如下:有三根柱子,标记为A、B和C,A柱上穿有n个大小 不同 的圆盘,最上面的圆盘最小,依次往下递增。 初始状态下,所有圆盘都按照大小从小到大的顺序堆叠在A柱上。目标是将所有圆盘移动到C柱上,并保持原有的大小顺序,同时遵守以下规则:一次只能移动一个圆盘。移动过程中,任何时刻大圆盘都不能放在小圆盘的上面。
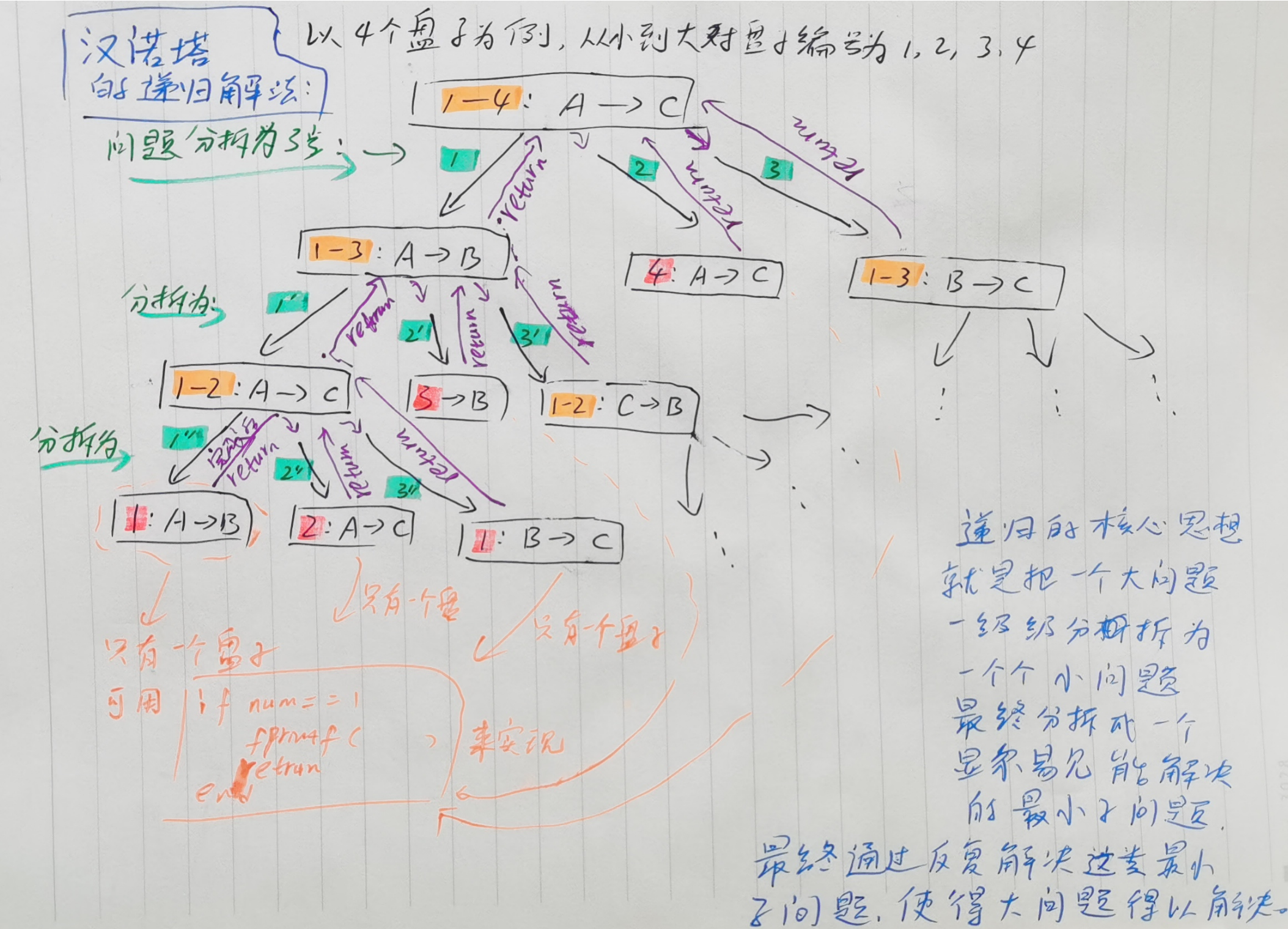
这个问题的经典解法是使用递归算法 。基本思路 是将问题划分为三个子问题:将n-1个圆盘从A移动到B,将最大的圆盘从A移动到C,最后将n-1个圆盘从B移动到C。这一过程可以递归地应用于子问题,直到圆盘数量为1时,可以直接移动。递归的结束条件是当只有一个圆盘时,直接将它从起始柱移动到目标柱。n阶汉诺塔问题最少共需要2的n次方减1步
汉诺塔问题不仅是一个有趣的数学谜题,而且它还展示了递归算法在解决问题时的简洁性和高效性。这个问题也经常被用作计算机科学和算法设计的教学案例。
参考:https://www.zhihu.com/question/421523155/answer/2314542265
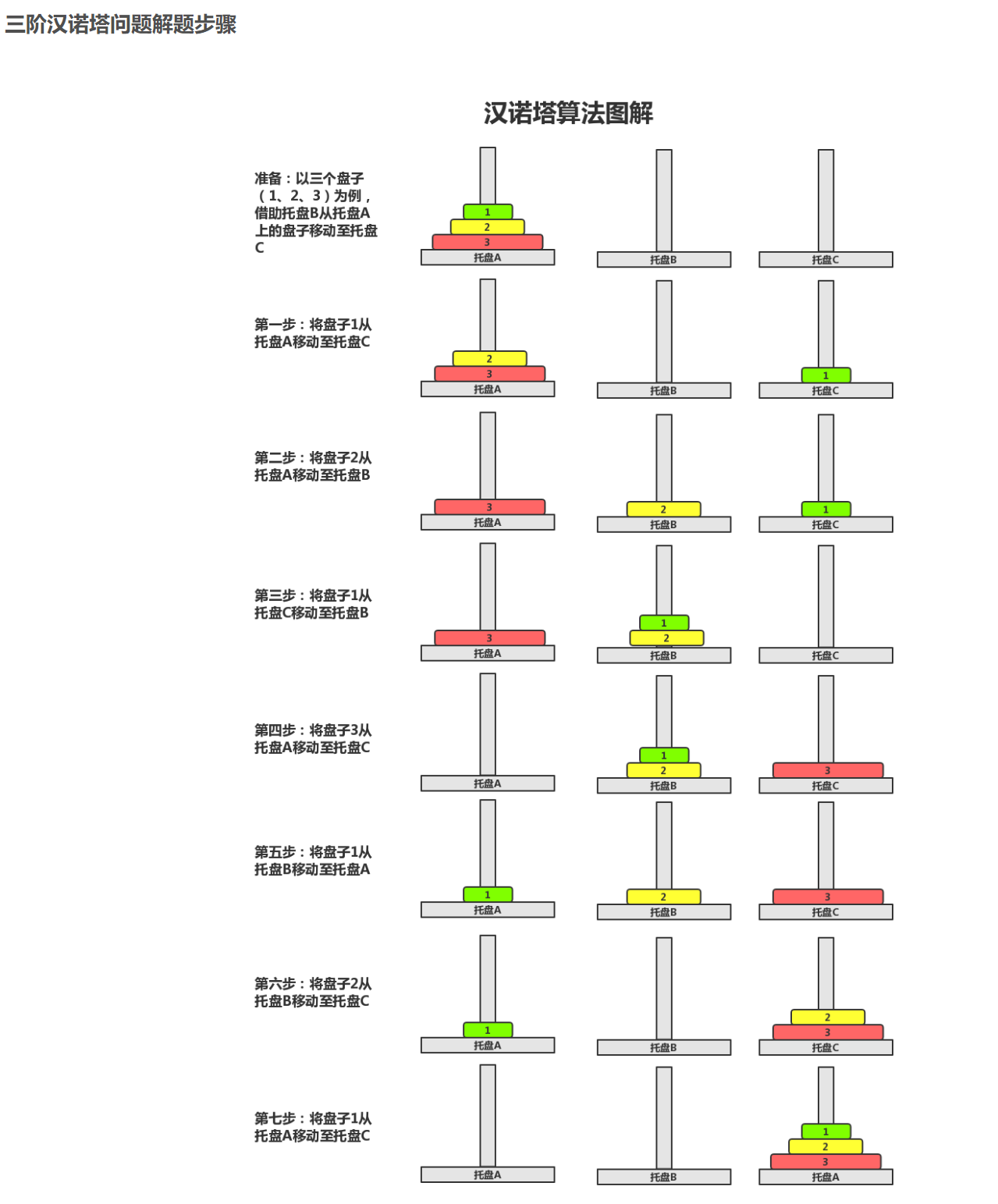
请编写一个名为 hanno 的函数,给出初始num个盘子在A柱,最终移动到C柱的全部流程。
hanno(3, 'A' , 'B' , 'C' )
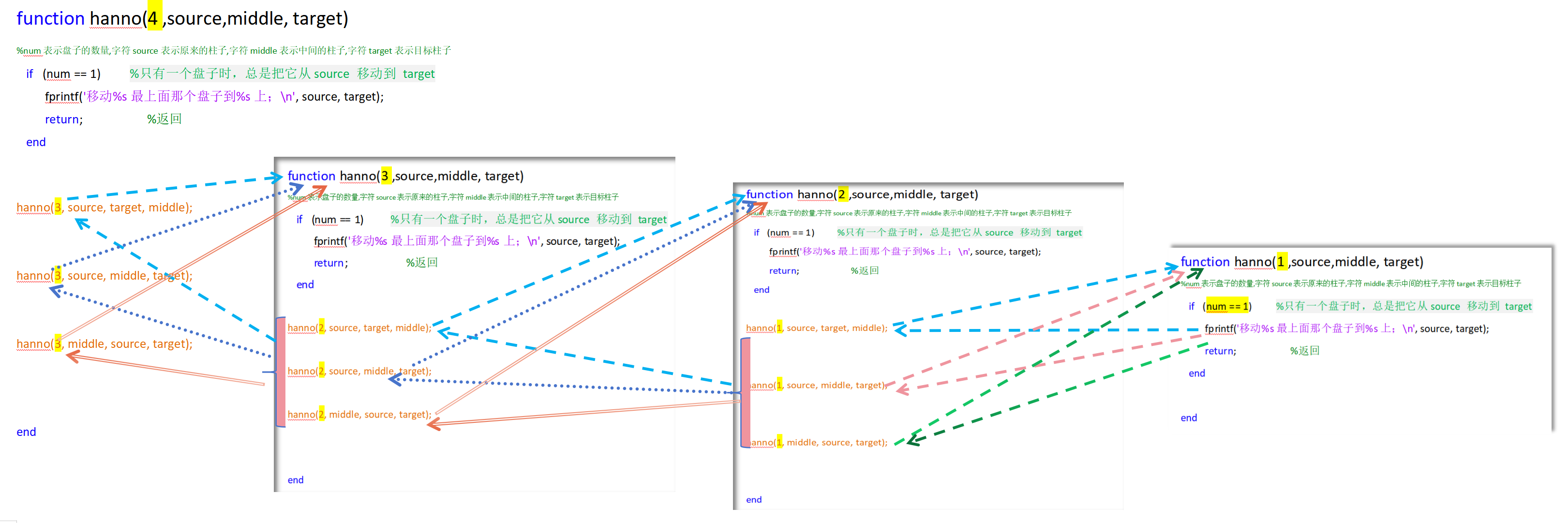
function hanno(num,source,middle, target)
%num表示盘子的数量,字符source表示原来的柱子,字符middle表示中间的柱子,字符target表示目标柱子
if (num == 1) %只有一个盘子时,总是把它从source 移动到 target
fprintf( '移动%s最上面那个盘子到%s上;\n' , source, target);
return ; %返回
end
hanno(num - 1, source, target, middle); %例:只有2个盘子时,就让 hanno帮忙先把1号 盘从A移到B
hanno(num - 1, source, middle, target); %再让 hanno帮忙先把2号 盘从A移到C
hanno(num - 1, middle, source, target); %再让 hanno帮忙先把1号 盘从B移到C
end
练习3:把上节课绘制彩色随机图的代码改造成函数,并调用这个函数。
function randcolor(k1,k2,n,m)
% randcolor的作用是生产随机彩图
% 调用方式为randcolor(k1,k2,n,m),其中k1彩图的行数,k2彩图的列数,n每个单元格的像素值,m彩图的刷新次数
rgb=zeros(k1*n,k2*n,3); %rgb的初始化
for t=1:m %刷新m次,每次都重新生成新的随即彩图
for ii=1:k1 %ii代表行
for jj=1:k2 %JJ代表列
rgb((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = ones(n ,n ,3).*rand(1,1,3);
end
end
imshow(rgb) %显示彩图rgb
hold on %保持彩图窗口不动
pause(2) %持续2秒
end
end
=====================
作业:
作业1:设计一个 函数,调用此函数可以返回 矩阵(或者数组)中最大值以及最小值元素和平均值等。
输入参数A为输入的一个矩阵或者数组。
返回参数ma,mi为找到的矩阵A中的最大值与最小值。
返回参数ma,mi,ma_R,ma_C,mi_R,mi_C为最大值与最小值所对应的行号和列号。
返回参数pjz为矩阵A中的平均值。
要求: 不能用matlab自带的max/min等现成的函数 ,要自己用for循环、if判断、>=,等方式寻找最大与最小值。
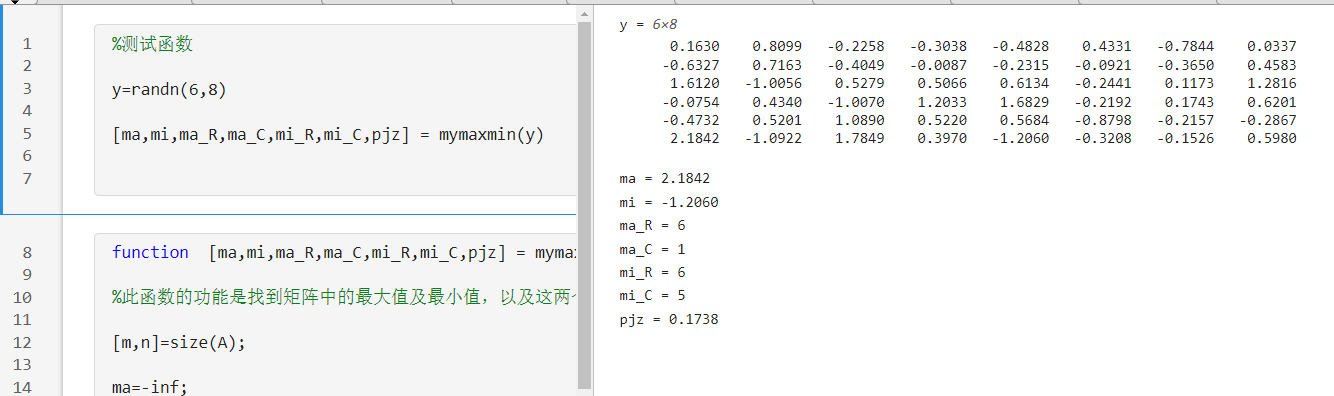
function [ma,mi,ma_R,ma_C,mi_R,mi_C,pjz ] = mymaxmin (A )
%此函数的功能是找到矩阵中的最大值及最小值,以及这两个最值对应的坐标。
[n,m]=size(A)
........
end
测试效果如下:
用正态分布的随机矩阵测试:
答案提示:
function [ma,mi,ma_R,ma_C,mi_R,mi_C,pjz] = mymaxmin(A)
%此函数的功能是找到矩阵中的最大值及最小值,以及这两个最值对应的坐标。
[m,n]=size(A);
ma=-inf;
mi=inf;
total=0;
for i=1:m
for j=1:n
???
end
end
pjz=total/(m*n);
end
作业2: 试着看看能否自己设计一个函数,比如命名为 myfind.m, 实现matlab自带的find函数的类似功能?
function [ A_k , A_k _R , A_k _C myfind A , k , w
%此函数的功能是找到矩阵 A 中的大于 k(当W=1时),或者小于 k(当W=0时)的元素 。
.......
end
输入参数 A 为输入的一个矩阵或者数组。
输入参数W 只能为1或者0;W W
返回参数 A_k , A_k_R , A_k_C 为 3个数组 ,分别记录按照要求找到的元素,以及这些元素对应的行号和列号 。
要求:
(1)不能用matlab自带的find等现成的函数,要自己用for循环、if判断、>=,等方式寻找最大与最小值。
(2)如果对方输入的参数w 不是0或者1,则输出报警,并返回空数组。
(3)如果没有找人任何符合要求的元素,则打印输出一句话“很抱歉,没有找到符合条件的元素。”
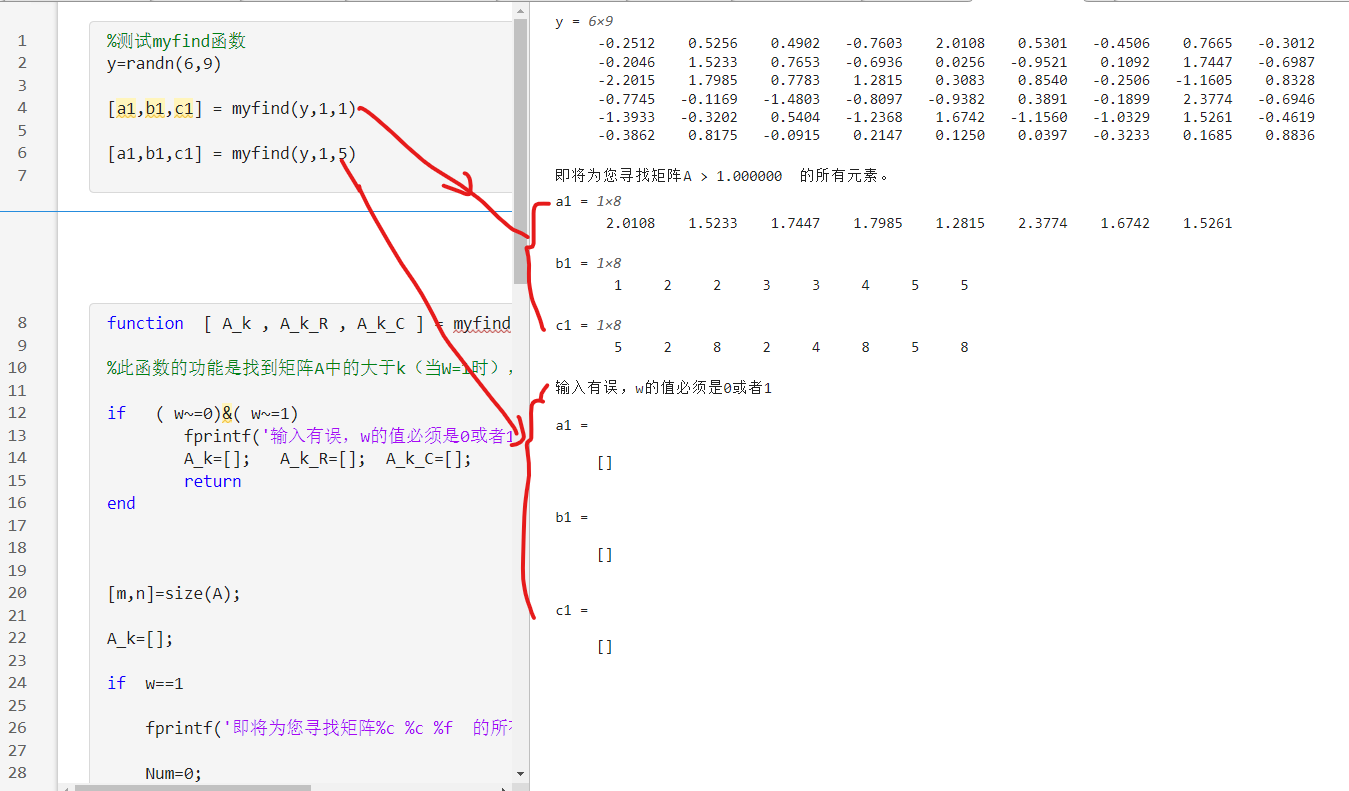
函数测试效果如下:
答案提示:
function [ A_k , A_k_R , A_k_C ] = myfind(A , k , w )
%此函数的功能是找到矩阵A中的大于k(当W=1时),或者小于k(当W=0时)的元素。
if ??
fprintf( '输入有误,w的值必须是0或者1 \n' );
A_k=[]; A_k_R=[]; A_k_C=[];
return
end
[m,n]=size(A);
A_k=[ ];
if w==1
fprintf('即将为您寻找矩阵%c %c %f 的所有元素。 \n' ,'A' ,'>',k);
Num=0;
for ii=1:m
for jj=1:n
??
end
end
end
if w==0
fprintf('即将为您寻找矩阵%c %c %f 的所有元素。 \n' ,'A' ,'<',k);
Num=0;
for ii=1:m
for jj=1:n
??
end
end
end
end
作业3:编写一个名为is_prim()的函数。此函数可以实现的功能为: 对输入的一个大于1的整数进行判断其是否是素数,如果是素数则返回1,否则返回0; 如果输入N是小于2的正整数,或者N是非整数,则返回y=[ ]
函数调用的效果如下图:
作业4:编写一个名为函数zxgbs(X1,X2)的函数,如下:
function y = zxgbs(X1,X2)
....
....
end
实现求最小公倍数的功能,即调用该函数,输入两个正整数x1,x2,则返回这两个正整数的最小公倍数。如:zxgbs(10,15),则返回y=30;
提示:两个正整数的最小公倍数,等于,这两个正整数的乘积,除以这两个正整数的最大公约数。 最大公约数可以使用for循环来寻找。
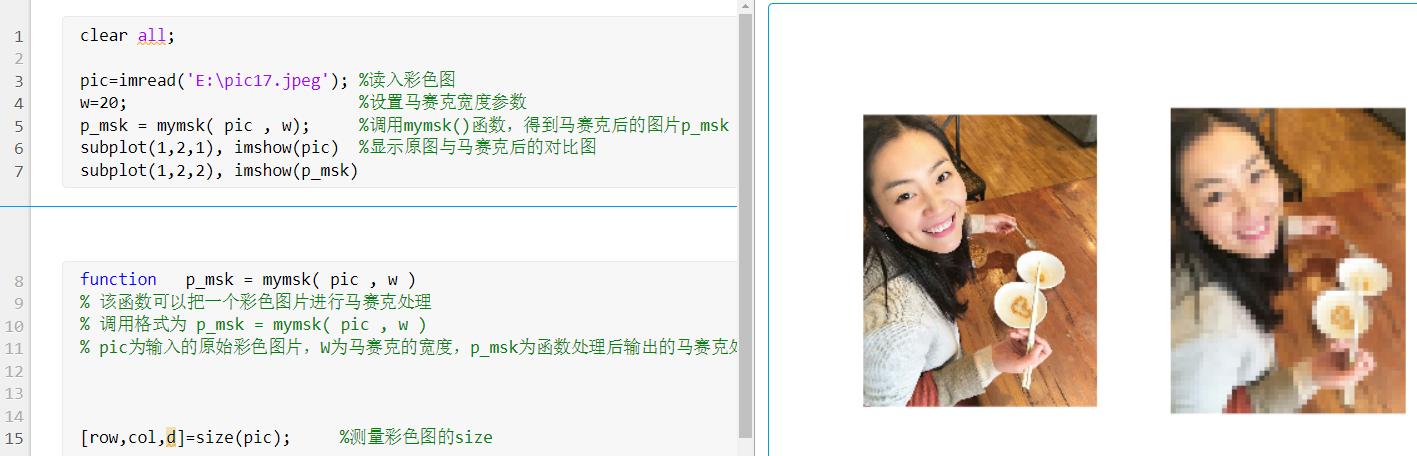
作业5:编写一个彩色图像的马赛克处理函数
调用格式为 p_msk = mymsk( pic , w ) pic为 输入的原始彩色图片, W为 马赛克的宽度, p_msk为函数处理后 输出的马赛克处理后的图片 。
mymsk
步骤1: 把图片的行数和列数截取为100的整数倍,得到pic_new,比如:如果原始图片大小为630*540,则pic_new 为600*500。
步骤2: pic_new 的r,g,b三个通道抽出,分别给pic_new _r, pic_new _g, pic_new _b, 。
步骤3: pic_new_r, pic_new_g, pic_new_b这三个灰度图, 按照w w ;
步骤4: 再把步骤3 利用cat()函数重新拼接成一个彩色图p_msk
在主程序中调用后的效果如下图:
作业6:素数问题综合练习
(1)编写函数求解给定整数N之内的所有素数;
要求:采用主函数与子函数的模式,子函数is_prime(K)用来判断k是否是素数,如果是,则返回1,否则返回0;主函数则用来遍历2-N之间的每一个整数,如果该数是素数则记录到数组中,并且计数器加1,最终函数返回记录了N之内的所有素数的数组,以及素数的个数。
以下为(1)的提示性代码,供参考;
function [prime,num] = prime_N (N) %主函数 prime_N()
%此函数用于找出给定的N之内的所有素数
% 函数 [prime,num] = prime_N(N) 中,返回的数组prime记录了N之内的所有素数,
%num记录了N之内的素数的总数。
num=0; %Num记录发现的素数的个数,初始值为0
%采用for循环,挨个判断2-N之间的每一个数是否为素数。
% 判断某个数是否为素数的任务通过调用子函数is_prime 完成。
end
function y = is_prime %子函数is_prime
%子函数 is_prime(N) 用于判断给定的数N是否是素数
%如果给定的N是素数,则返回1,否则返回0
flag=0; %用flag来记录N的因子的个数,初始值为0
m=fix(sqrt(N)); %寻找N的因子时,只需要试到fix(sqrt(N))
%for循环来历遍2-m之间的所有数,如果N能被2-m之间的某个数整除,说明找到了一个因子,则因子记录器flag加1,并跳出循环
% 如果flag==0 ,说明前面没有找到 N的因子,既N是素数,返回1,否则返回0
end
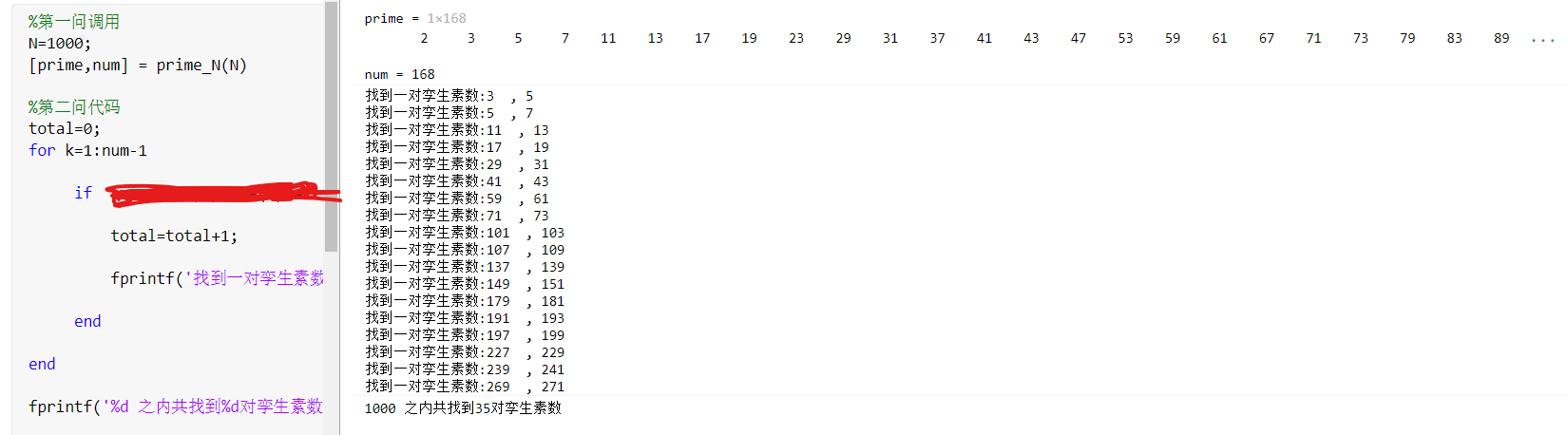
(2)编写一段代码,通过调用prime_N()函数,找出1000之内的所有孪生素数 对,并输出这些孪生素数对。 该问的提示性代码:
N=1000;
[prime,num] = prime_N(N)
total=0;
for k=1:num-1
if ??
total=total+1;
fprintf('找到一对孪生素数:%d , %d \n' ,prime(k), prime(k+1) );
end
end
fprintf('%d 之内共找到%d对孪生素数 \n' ,N, total );
最终调用效果如下(参考 ):
作业7: 编写程序,输入一个大于2的正整数,则输出该正整数的3x+1序列。
方法1:采用普通脚本程序形式。
用input函数得到一个正整数,然后求出该数的3x+1序列,然后按照每行10个数的形式输出屏幕,再输出该3x+1序列的长度、最大值、最大值与初始值的比值。
效果如下:
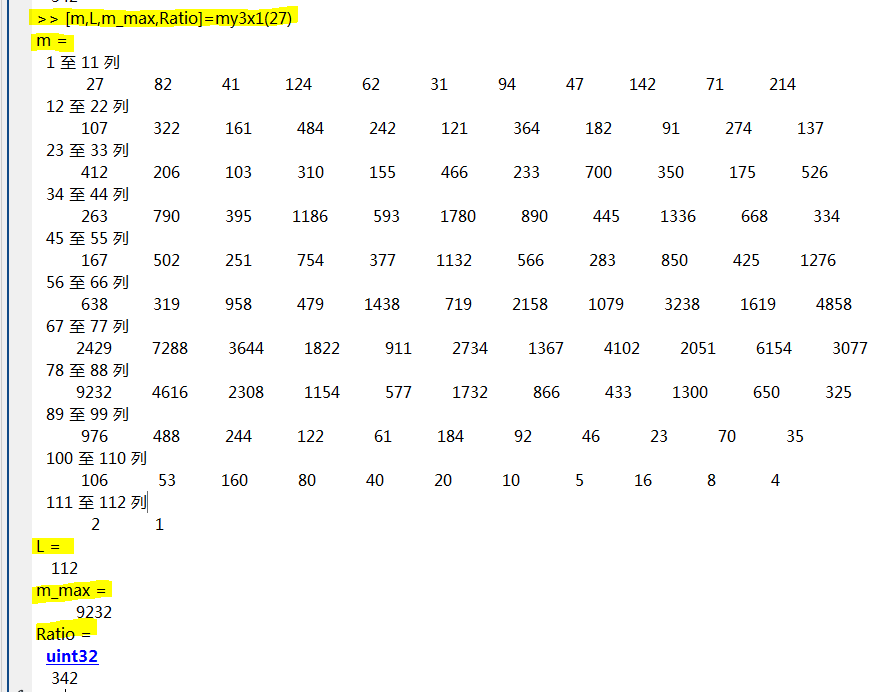
方法2:采用函数形式。 编写一个名为 my3x1( ) 的函数,输入正整数N,输出该数的3x+1序列的数组x,序列的长度L(既数组m的长度),序列中的最大值m_max,序列中最大值与初始值的比值。
function [m,L,m_max,Ratio]=my3x1(N)
........
........
end
调用该函数,效果如下:
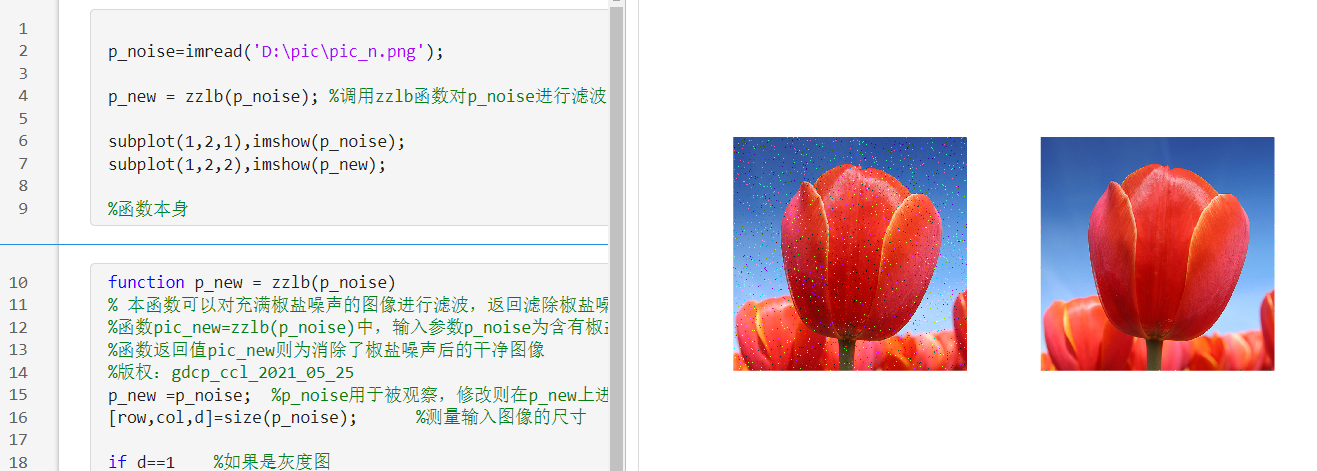
作业8:编写一个中值滤波函数:zzlb() , 用于滤除图像的椒盐噪声
%以下代码为提示性代码:
function pic_new= zzlb (pic_old)
% 本函数可以对充满椒盐噪声的图像进行滤波,返回滤除椒盐噪声后的干净图像
%函数 pic_new= zzlb(pic_old)中,输入参数pic_old为含有椒盐噪声的原始图像(uint8格式)
% 函数返回值pic_new则为消除了椒盐噪声后的干净图像
[n,m,d]=size(pic_old) %获取图像 pic_old的维度
%判断d等1还是等于3?如果等于1,则 pic_old 为灰度图,执行以下操作
%采用双层for循环,对 pic-old进行中值滤波,得到滤波后的干净图像pic_new
..........
..........
for i=2:n-1 %在p_noise的2到row-1行,2到col-1列的区域遍 历
for j=2:m-1
..........
..........
..........
%如果d=3,则表示pic_old为彩色图,这时,需要对RBG每一个通道都进行上述类似的中值滤波,
%得到3个滤波后的2维数组,再合并成一个3维数组,即彩色的pic_new
..........
..........
..........
end
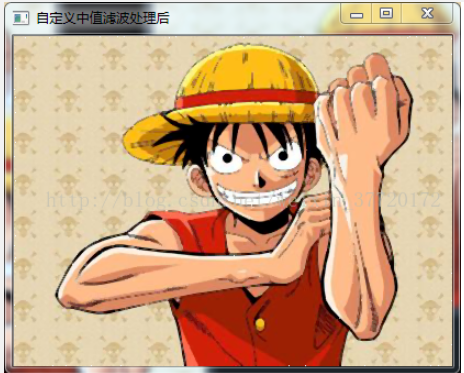
调用和使用zzlb 函数效果如下图 :
作业所用含椒盐噪声图像如下:
中值滤波与椒盐噪声基础知识
(1) 椒盐噪声 (salt-and-pepper noise) : 椒盐噪声 是由图像传感器,传输信道,解码处理等产生的黑白相间的亮暗点噪声。 所谓椒盐,椒就是黑,盐就是白,椒盐噪声就是在图像上随机出现黑色(0)与白色(255)的像素。椒盐噪声是一种因为信号脉冲强度引起的噪声,产生该噪声的算法也比较简单。
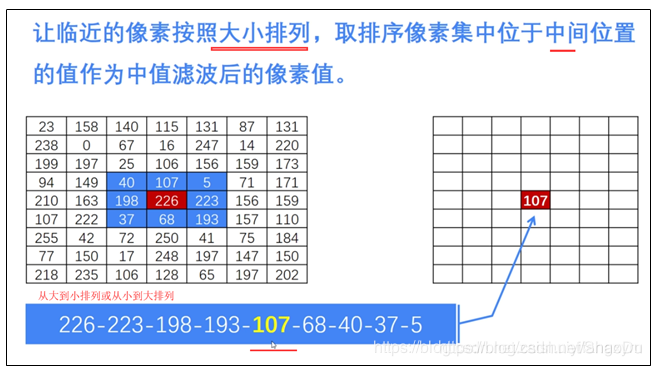
(2)中值滤波 什么是中值?在一连串数字{9,6,7,1,4}中,数字6就是这串数字的中值(中位数)。由此我们可以应用到图像处理中。
中值滤波: 简单来说,假如怀疑某点被椒盐噪声破坏了(灰度值变成了0或255),那么就是用这个点的周边的像素的中位值来代替当前像素点的值;即,将滤波器范围内的像素的灰度值,进行排序,选出中央值作为这个像素的灰度值
具体过程: 一般采用3*3的区域(这样恰好当前点位于九宫格的中心)在图像上按照从左到右从上到下的方式扫过(历遍)整个图像;扫描时,中心点 每次停到一个位置就检测一下该点是否是潜在的噪声点?如果是就做以下操作: 把当前点作为中心点,构建一个3*3的临时小矩阵,对矩阵里面的9个像素的灰度值进行排序, 找出中位数,最后将这个 3*3区域的 中心点的灰度值用刚才找到的中位数来更新。
其中3*3区域(九宫格)内的中位数g的产生过程如下:
(3)椒盐噪声的中值滤波: 对于椒盐噪声,因为噪点的值往往很极端,要么值为255的白点,要么是值为0的黑点,所以执行中位数滤波时,并不是对每一个像素点都要进行中位数滤波,只有满足当前点为255或0时,才执行前述的中位数滤波。这样可以在滤波的同时,减小因为滤波引起的图像模糊。
效果图:
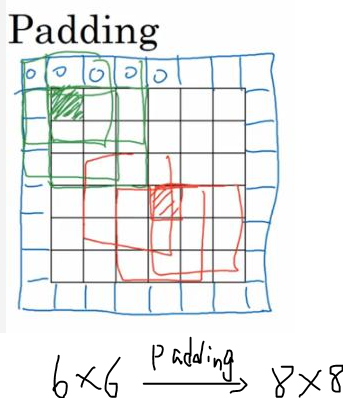
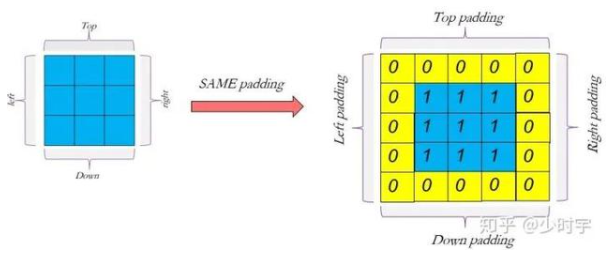
(4)图像处理时的边缘的填充问题: 在对图像应用滤波器进行过滤时,边界填充问题是一个需要处理的问题。
一般来说,有3种处理的方法。
1. 不做边界处理 不对图像的边界作任何处理,在对图像进行滤波时,滤波器没有作用到图像的四周,因此图像的四周没有发生改变。
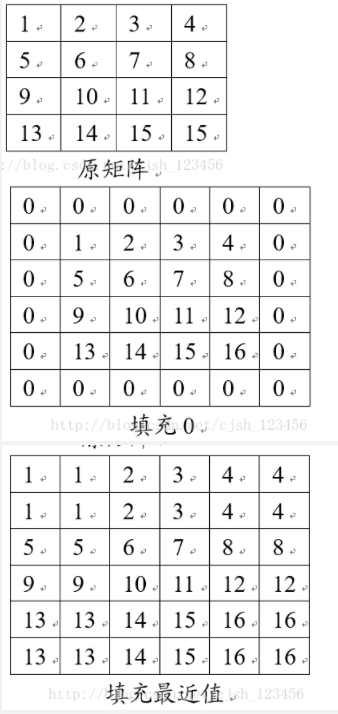
2. 填充0 对图像的边界做扩展,在扩展边界中填充0,对于边长为2k+1的方形滤波器,扩展的边界大小为k,若原来的图像为[m, n],则扩展后图像变为[m+2k, n+2k]。进行滤波之后,图像会出现一条黑色的边框。
3. 填充最近像素值 扩展与 填充0 的扩展类似,只不过填充0的扩展是在扩展部分填充0,而这个方法是填充距离最近的像素的值。
================================
================================
课外补充:
思考:如何设置函数的参数为可变数目的参数?
MATLAB中的nargin与varargin (1)nargin的用法:
nargin:number of function input arguments,指的是一个函数的输入变量的个数。
用法:nargin或着nargin(fx), 其中fx指的是一个函数名或着函数句柄。
当一个函数的参数中含有varargin变量时,这时候返回值为负。
下面举例说明:
用于nargin:
function c = addme(a, b)
返回的结果为 a + b。
用到nargin(fx):
fx = 'addme'; 当含有 varargin参数时,
function mynewplot(x, y, varargin) (2)varargin的用法:
varargin:Variable-length input arguments list. 即指的是变输入参数列表;
varargin 就是一个输入 变量,它可以是任意个不定个数的输入参数。要求:第一,指明它用小写的字母表示;第二,在函数的参数列表中,varargin放在最后面。 当函数执行时,varargin就是一个1*n的cell数组。下面我们举例说明:
第一个例子:
function varlist( vargarin)
第二个例子:
function varlist2(x, y, varargin)
例1:利用nargin、varargin函数来改进冒泡排序算法,使得输入参数可变。
function B = mysort(A , varargin)
%这是一个冒泡排序算法,对输入的数组A进行排序
%order=1,表示按照从小到大进行排序,如果order=0,则从大到小排序
n=length(A); %测量输入数组A的长度
if nargin==1 %当输入参数数量为1时,order=1 order=1;%否则,order的值为输入的第二个参数(可变参数varargin)的内容 order=varargin{1}; if order==1
for ii=1:n-1 % ii表示趟数
for jj=1:n-ii % 开始两两比较,n-ii表示每一趟内部需要进行的两两比较的总数目
if A(jj)>=A(jj+1) %如果左边元素大于右边元素,则交换两者位置。
p=A(jj);
A(jj)=A(jj+1);
A(jj+1)=p;
end
end
end
end
if order==0
for ii=1:n-1 % ii表示趟数
for jj=n:-1:ii+1 % 开始两两比较,n-ii表示每一趟内部需要进行的两两比较的总数目
if A(jj)>=A(jj-1) %如果左边元素大于右边元素,则交换两者位置。
p=A(jj);
A(jj)=A(jj-1);
A(jj-1)=p;
end
end
end
end
B = A;
end
例2: 假设我们想生成一个 nxm 阶的 Hilbert 矩阵, 它的第 i 行第 j 列的元素值为 1/(i+j-1)。我们想在编写的函数中实现下面几点:
如果只给出一个输入参数,则会自动生成一个方阵,即令 m=n
在函数中给出合适的帮助信息,包括基本功能、调用方式和参数说明
检测输入和返回变量的个数,如果有错误则给出错误信息
如果调用时不要求返回变量,则将显示结果矩阵。其实在编写程序时养成一个好的习惯,无论对程序设计者还是对程序的维护者、使用者都是大有裨益的。
function A=myhilb(n, m)
%MYHILB a demonstrative M-function. %A=MYHILB(N, M) generates an N by M Hilbert matrix A. %A=MYHILB(N) generates an N by N square Hilbert matrix. %MYHILB(N,M) displays ONLY the Hilbert matrix, but do not return any %matrix back to the calling function.
if nargout>1,
error('Too many output arguments.');
end
if nargin==1,
m=n;
elseif nargin==0 | nargin>2
error('Wrong number of iutput arguments.');
end
A1=zeros(n,m);
for i=1: n
for j=1:m
A1(i,j)=1/(i+j-1);
end
end
这样规范编写的函数用 help 命令可以显示出其帮助信息:
>> help myhilb MYHILB a demonstrative M-function.
有了函数之后,可以采用下面的各种方法来调用它,并产生出所需的结果。
>> A=myhilb(3,4)
数组的全排列实现:
全排列是将一组数按一定顺序进行排列,如果这组数有n个,那么全排列数为n!个。现以{1, 2, 3, 4, 5}为例说明如何编写全排列的递归算法。
1、首先看最后两个数4, 5。 它们的全排列为4 5和5 4, 即以4开头的5的全排列和以5开头的4的全排列。
由于一个数的全排列就是其本身,从而得到以上结果。
2、再看后三个数3, 4, 5。它们的全排列为3 4 5、3 5 4、 4 3 5、 4 5 3、 5 3 4、 5 4 3 六组数。
即以3开头的和4,5的全排列的组合、以4开头的和3,5的全排列的组合和以5开头的和3,4的全排列的组合.
从而可以推断,设一组数p = {r1, r2, r3, ... ,rn}, 全排列为perm(p),pn = p - {rn}。
因此perm(p) = r1perm(p1), r2perm(p2), r3perm(p3), ... , rnperm(pn)。当n = 1时perm(p} = r1。
为了更容易理解,将整组数中的所有的数分别与第一个数交换,这样就总是在处理后n-1个数的全排列。
%全排列
clear
x=[1 2 3 4];
N=length(x);
myperm(x,1,N)
function myperm(s,n1,n2)
if n1==n2
fprintf( 'str is -------:%s\n' ,num2str(s))
else
for k=n1:n2
temp=s(n1);
s(n1)=s(k);
s(k)=temp;
myperm(s,n1+1,n2);
end
end
end
function qpl= quanpailie(nums)
%UNTITLED2 此处显示有关此函数的摘要
% 此处显示详细说明
global temp;
global qpl;
if length(temp)==length(nums)
qpl=[qpl;temp]
temp=[];
else
for i=1:length(nums)
if sum(temp==nums(i))==1
continue
else
temp=[temp,nums(i)]
end
temp=quanpailie(nums);
end
end
end
对递归的理解的要点主要在于放弃!
放弃你对于理解和跟踪递归全程的企图,只理解递归 两层之间的交接,以及递归终结的条件。
想象你来到某个热带丛林,意外发现了十层之高的汉诺塔 。正当你苦苦思索如何搬动它时,林中出来一个土著,毛遂自荐要帮你搬塔。他名叫二傻,戴着一个草帽,草帽上有一个2字,号称会把一到二号盘搬到任意柱。
你灵机一动,问道:“你该不会有个兄弟叫三傻吧?”
你说:”三傻,你帮我把头三个盘子移到c柱吧。“
由于天气炎热你开始打瞌睡。朦胧中你没看见二傻是怎么工作的,二傻干完以后,走入林中 大叫一声:“老三,我干完了!”
三傻 出来,把三号盘从A搬到B,然后又去叫二傻:“老二,帮我把头两个盘子搬回A!”
余下的我就不多说了,总之三傻其实只搬三号盘,其他叫二傻出来干。最后一步是三傻把三号盘搬到C,然后呼叫二傻来把头两个盘子搬回C
事情完了之后你把三傻叫来,对他说:“其实你不知道怎么具体一步一步把三个盘子搬到C,是吧?”
三傻不解地说:“我不是把任务干完了?”
你说:“可你其实叫你兄弟二傻干了大部分工作呀?”
三傻说:“我外包给他和你屁相干?”
你问到:“二傻是不是也外包给了谁?“
三傻笑了:“这跟我有屁相干?”
你苦苦思索了一夜,第二天,你走入林中大叫:“十傻,你在哪?”
一个头上带着10号草帽的人,十傻,应声而出:“老爷,你有什么事?”
“我要你帮把1到10号盘子搬到C柱“
“好的,老爷。“十傻转身就向林内 走。
“慢着,你该不是回去叫你兄弟九傻吧“
“老爷你怎么知道的?“
“所以你使唤他把头九个盘子搬过来搬过去,你只要搬几次十号盘 就好了,对吗?“
“对呀!“
“你知不知道他是怎么干的?“
“这和我有屁相干?“
你叹了一口气,决定放弃。十傻开始干活。树林里充满了此起彼伏的叫声:“九傻,来一下!“ “老八,到你了!““五傻!。。。“”三傻!。。。“”大傻!“
你注意到大傻从不叫人,但是大傻的工作也最简单,他只是把一号盘搬来搬去。
若干年后,工作结束了。十傻来到你面前。你问十傻:“是谁教给你们这么干活的?“
十傻说:“我爸爸。他给我留了这张纸条。”
他从口袋里掏出一张小纸条,上面写着:“照你帽子的号码搬盘子到目标柱。如果有盘子压住你,叫你上面一位哥哥把他搬走。如果有盘子占住你要去的柱子,叫你哥哥把它搬到不碍事的地方。等你的盘子搬到了目标,叫你哥哥把该压在你上面的盘子搬回到你上头。“
你不解地问:“那大傻没有哥哥怎么办?“
十傻笑了:“他只管一号盘,所以永远不会碰到那两个‘如果’,也没有盘子该压在一号上啊。”
但这时他忽然变了颜色,好像泄漏了巨大的机密。他惊慌地看了你一眼,飞快地逃入树林。
第二天,你到树林里去搜寻这十兄弟。他们已经不知去向。你找到了一个小屋,只容一个人居住,但是屋里有十顶草帽,写着一到十号的号码。