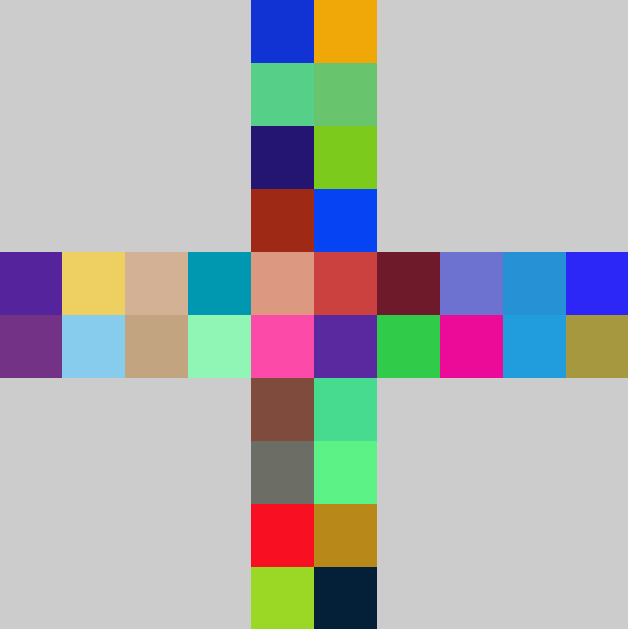1. 数学运算中的模除法和舍入

   mod	除后的余数（取模运算）
   rem	除后的余数
   idivide	带有舍入选项的整除
   ceil	朝正无穷大四舍五入
   fix	朝零四舍五入
   floor	朝负无穷大四舍五入
   round	四舍五入为最近的小数或整数

(1) ceil( )与floor( ) 

ceil( ):    朝正无穷舍入到最近的整数(天花板方向)

floor( ):   朝负无穷舍入到最近的整数(地板方向)

Y = ceil(X)将 X的每个元素四舍五入到大于或等于该元素的最接近整数。

Y = ceil(t)将 duration数组 t的每个元素四舍五入到大于或等于此元素的最接近的秒数。

Y = floor(X) 将 X 的每个元素四舍五入到小于或等于该元素的最接近整数。

Y = floor(t) 将 duration 数组 t 的每个元素四舍五入到小于或等于此元素的最接近的秒数。

>> X = [-1.9 -2.3 -0.47 -0.7; 5.6 4.2 0.35 0.8]
X =
   -1.9000   -2.3000   -0.4700   -0.7000
    5.6000    4.2000    0.3500    0.8000
    
>> Y1 = ceil(X)
Y1 =
    -1    -2     0     0
     6     5     1     1
     
>>  Y2= floor(X)
Y2 =
    -2    -3    -1    -1
     5     4     0     0

(2) fix 朝零四舍五入到最近的整数（只保留整数部分）

语法： Y = fix(X)    

!→|0|←!   向零方向舍入.

Y = fix(X)将X的每个元素朝零方向四舍五入为最近的整数。此操作实际上是通过删除 X中每个数的小数部分，将它们截断为整数：对于正数，fix的行为与 floor相同。对于负数，fix 的行为与 ceil相同。

将矩阵元素向零取整

X = [-1.9 -3.4; 1.6 2.5; -4.5 4.5]

X =
   -1.9000   -3.4000
    1.6000    2.5000
   -4.5000    4.5000

Y = fix(X)

Y = 
    -1    -3
     1     2
    -4     4

(3) 舎入函数 round(a)（四舍五入）

round:四舍五入为最近的小数或整数

Y = round(X)将 X的每个元素四舍五入为最近的整数。在对等情况下，即有元素的小数部分恰为 0.5时，round函数会偏离零四舍五入到具有更大幅值的整数。Y = round(X,N) 四舍五入到 N位数：N > 0：舍入到小数点右侧的第 N位数。

N = 0：四舍五入到最接近的整数。

N < 0：舍入到小数点左侧的第 N位数。

例：

x=[ 1.3   4.8  0.7  0.1;
     -1.3 -4.8 -0.7 -0.1]
y1=ceil(x)
y2=floor(x)
y3=round(x)
y4=fix(x)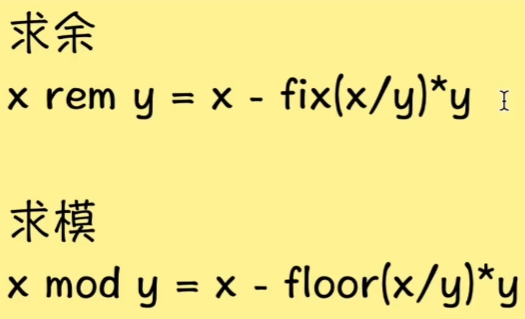

4)模除求余数函数: mod(x,y) , rem(x,y)

取模运算:mod

语法:b = mod(a,m)

b = mod(a,m) 返回 a 除以 m 后的余数，其中 a 是被除数，m 是除数。此函数通常称为取模运算，表达式为 b = a - m.*floor(a./m)。mod 函数遵从 mod(a,0) 返回 a 的约定。

b = mod(23,5)

b = 3

除后的余数:rem

语法:r = rem(a,b)

r = rem(a,b) 返回 a 除以 b 后的余数，其中 a 是被除数，b 是除数。此函数通常称为求余运算，表达式为 r = a - b.*fix(a./b)。rem 函数遵从 rem(a,0) 是 NaN 的约定。

例1：计算 23 除以 5 后的余数。

a = 23;

b = 5;

r = rem(a,b)

r = 3

例2： 计算一个含正负值的整数集被除后的余数。请注意，非零结果的符号与被除数相同。

>>  a = [-4.5  -1   7  9.3];
b = 3;
r = rem(a,b)
r =
      -1.5000   -1.0000   1.0000   0.3000

其实取模和取余在目标上是一致的，但是因为语言对取余和取模上定义的不同，导致得到的结果不同。

对取余和取模定义不同的语言中，两者的不同点只有一个

取余运算在计算商值向0方向舍弃小数位
      取模运算在计算商值向负无穷方向舍弃小数位
同时，也可以这样理解：

• 取余，遵循尽可能让商大的原则

• 取模，遵循尽可能让商小的原则

从上面的区别可以总结出，取余（rem）和取模（mod）在被除数、除数同号时，结果是等同的，异号时会有区别，所以要特别注意异号的情况。

下面来看一些例子：

取模

       5 mod 3 = 2
      -5 mod 3 =   1
       5 mod -3 = -1
      -5 mod -3 = -2

取余

      5 rem 3 = 2     

    -5 rem 3 = -2
      5 rem -3 = 2
     -5 rem -3 = -2

%rem与mod对比

>> a = [-4  -1  7  9];

>> b = 3;

>> r = rem(a,b)

r =

      -1    -1     1     0

>> m=mod(a,b)

m =

       2     2     1     0

%rem与mod对比——用负除数除后的余数

>> a = [-4 -1 7 9];

>>b = -3;

>>r = rem(a,b)

>>m=mod(a,b)

r =

    -1    -1     1     0

m =

    -1    -1    -2     0

练习：找出数组X=1:100 中所有不能被3或5或7整除的整数的个数。

x=1:100

y1= mod(x,3)==0

y2= mod(x,5)==0

y3= mod(x,7)==0

y=~(y1|y2|y3)

n=sum(y)

5)绝对值函数abs(a)

x = [0 -1 -2 4 -4 9]
abs_x = abs(x)

x =
     0    -1    -2     4    -4     9    
abs_x =
     0     1     2     4     4     9

6)数组指数exp(a) 将矩阵元素作为e的幂exp(a)=e.^a

a = [1  -3  3 ; 2  -1  6]
result_a = exp(a)

a =
     1    -3     3
     2    -1     6
result_a =
    2.7183    0.0498   20.0855
    7.3891    0.3679  403.4288

7)平方根函数的使用 sqrt(a)

a=[2 5 8 9]
result_sqrt = sqrt(a)

a =
     2     5     8     9
result_sqrt =
    1.4142    2.2361    2.8284    3.0000

8)对数函数 自然对数 log(a), log2(a), log10(a)

a = [12 3 7;-1 4 -2; 21 17 -5]
result_log     = log(a)
result_log2   = log2(a)
result_log10 = log10(a)

a =
    12     3     7
    -1     4    -2
    21    17    -5

result_log =
   2.4849             1.0986             1.9459          
    0 + 3.1416i     1.3863             0.6931 + 3.1416i
   3.0445             2.8332             1.6094 + 3.1416i

result_log2 =
   3.5850             1.5850             2.8074          
   0 + 4.5324i      2.0000             1.0000 + 4.5324i
   4.3923             4.0875             2.3219 + 4.5324i

result_log10 =
   1.0792             0.4771             0.8451          
    0 + 1.3644i     0.6021             0.3010 + 1.3644i
   1.3222             1.2304             0.6990 + 1.3644i

9)数制之间的转换
a=bin2dec('1011001')      %将二进制数转换成十进制数
b=dec2bin(18)                %将十进制数转换成二进制数
c=hex2dec('9A2B')          %将十六进制数转换成十进制数
d=dec2hex(97)                %将十进制数转换成十六进制数
e=base2dec('212',3)        %将任意进制数转换成十进制数


输出：
a =
    89
b =
    '10010'
c =
     39467
d =
    '61'
e =
     23

10)相位角函数angle(a) 以弧度表示.

a=[3+4i,5+5i;5+12i 3]
angle_a=angle(a)*(180/pi)    %将弧度转换为度数.

a =
   3.0000 + 4.0000i   5.0000 + 5.0000i
   5.0000 +12.0000i   3.0000          
   
angle_a =
   53.1301            45.0000
   67.3801            0

11)求复数的实部和虚部real(a),imag(a)

a=[7-8i  10+i ; 3  7+2i ; 12-6i  3]
realOFa = real(a)
imagOFa = imag(a)
realANDimag = real(a) + imag(a)*i

a =
   7.0000 - 8.0000i    10.0000 + 1.0000i
   3.0000                     7.0000 + 2.0000i
  12.0000 - 6.0000i     3.0000          

realOFa =
     7    10
     3     7
    12     3

imagOFa =
    -8     1
     0     2
    -6     0

realANDimag =
   7.0000 - 8.0000i  10.0000 + 1.0000i
   3.0000                   7.0000 + 2.0000i
  12.0000 - 6.0000i   3.0000

12)求复数共轭conj(a)

a=[7-8i 10+i;3 7+2i;12-6i 3]
conjOFa = conj(a)
realANDimag = real(a) - imag(a)*j

a =
   7.0000 - 8.0000i  10.0000 + 1.0000i
   3.0000                 7.0000 + 2.0000i
  12.0000 - 6.0000i   3.0000          

conjOFa =
   7.0000 + 8.0000i  10.0000 - 1.0000i
   3.0000                    7.0000 - 2.0000i
  12.0000 + 6.0000i   3.0000          

realANDimag =
   7.0000 + 8.0000i  10.0000 - 1.0000i
   3.0000                    7.0000 - 2.0000i
  12.0000 + 6.0000i   3.0000

13）.累加与累乘

>> x=1:10

x =

     1     2     3     4      5      6      7      8     9    10

>> y1=cumsum(x)

y1 =

     1     3     6    10    15    21    28    36    45    55

>>  y2=cumprod(x)

y2 =

      1      2      6    24      120   720   5040    40320    362880   3628800

14).matlab中sind、cosd、tand以角度为单位，sin、cos、tan函数等都是以弧度为单位.

对于三角函数计算，在系统默认函数前后面加"d"是直接进行角度计算，这里"d"代表"degree",例如sind(30) = 0.5,效果与sin(30*pi/180)一样，其他的有cosd、tand等。

附表：MATLAB内置的三角运算函数大全

正弦: sin,sind,sinpi,asin,asind,sinh,asinh

余弦: cos,cosd,cospi,acos,acosd,cosh,acosh

正切: tan,tand,atan,atand,atan2,atan2d,tanh,atanh

余割: csc,cscd,acsc,acscd,csch,acsch

正割: sec,secd,asec,asecd,sech,asech

余切: cot,cotd,acot,acotd,coth,acoth

斜边: hypot

转换: deg2rad,rad2deg,cart2pol,cart2sph,pol2cart,sph2cart

MATLAB内置的指数对数函数:

 exp,expm1,log,log10,log1p,log2,nextpow2,nthroot,pow2,reallog,realpow,realsqrt,sqrt

MATLAB内置的复函数: abs,angle,complex,conj,cplxpair,i,imag,isreal,j,real,sign,unwrap

===============================================

练习：

1. 验证魔方矩阵。

>>a=magic(10)

a =

    92    99     1     8    15    67    74    51    58    40

    98    80     7    14    16    73    55    57    64    41

     4    81    88    20    22    54    56    63    70    47

    85    87    19    21     3    60    62    69    71    28

    86    93    25     2     9    61    68    75    52    34

    17    24    76    83    90    42    49    26    33    65

    23     5    82    89    91    48    30    32    39    66

    79     6    13    95    97    29    31    38    45    72

    10    12    94    96    78    35    37    44    46    53

    11    18   100    77    84    36    43    50    27    59

>> sum( a(2 ,:) )

ans =

   505

>> sum( a(: ,5) )

ans =

   505

>> sum( diag(a) )

ans =

   505

>> sum( diag(rot90(a)) )

ans =

   505

2. 简单绘图

先生成维度相同的两个数组x,y，相当于确定了一组点的x-y坐标，然后用plot（X,Y）命令，把这些点连接起来并显示。就是函数y的图像了。

x=1:0.01:10;

y=sin(x).*cos(50*x);

plot(x,y,'r')                   % 参数‘r’表示用红色绘图

x=rand(1,50);

y=rand(1,50);

plot(x,y,'r*') 

==================================

         综合项目练习：生成随机彩色网格图

教学目标：通过本项目综合掌握随机函数、图形显示与绘图原理、矩阵的赋值等知识点。

1）repmat 复制矩阵

B = repmat(A,m,n)
       B = repmat(A,[m n])
       B = repmat(A,[m n p...])

%repmat 复制矩阵

A=randi([0,9],2,2)

B=zeros(10,10);

B(1 : 4 , 1 : 6)=repmat(A , 2 , 3);

B

%如果矩阵的一大片需要赋相同的值，则可以直接把某个值赋给矩阵的这个切片。

A=randi([0,9],2,2)

B=zeros(10,10) ;

B(1 : 4 ,1 : 6)=repmat(A , 2 , 3) ;

B(5 : 10 , 1 : 6)=1 ;

B(5 : 10 , 7 : 10)=2 ;

B

这是一个处理大矩阵且内容有重复时使用，其功能是以A的内容堆叠在（MxN）的矩阵B中，B矩阵的大小由MxN及A矩阵的内容决定，如果A是一个3x4x5的矩阵，有B = repmat(A,2,3)则最后的矩阵是6x12x5

2）imshow函数

通过下面代码，理解图像的存储格式，以及显示方式imshow

 imshow函数：

（1）作用： imshow函数可以把一个二维矩阵（灰度图）或者三维矩阵（彩图）以图片形式显示出来。

（2）处理的数据类型： imshow函数处理的矩阵的数据类型可以是uint8类型（数值范围0-255），和double类型（数值范围0-1）。

% imshow用法 

pic1=imread( ' F:\bird_gray.jpg ' ); %imread读取一个图片，并以矩阵方式存给变量pic

size(pic1)                          %显示矩阵pic的尺寸

class(pic1)                         %显示矩阵pic的数据类型，默认为uint8类型

pic2=double(pic1)/255;    %思考:为啥要除以255？可替换为im2double(I)

class(pic2)

imshow(pic1);   %把矩阵pic1(uint8类型)当成图片来显示

imshow(pic2);   %把矩阵pic2（double类型）当成图片来显示

imtool(pic1);      %把矩阵pic当成图片，并用imtool 工具来探索图片信息。

Matlab图像处理中mat2gray、im2double和double的区别:

（1）double(I):直接将图像I的灰度数据转换为double类型；是对矩阵I进行双精度化处理，double的范围是-4.1143~476.1737；就是简单地把一个变量类型转换成double类型，数值大小不变；
比如 a=6 是个unit8类型的话，double（a）的结果还是6，不过现在这个6是double类型的。

（2）im2double(I):将灰度图像I转换成double类型，必要时将数据rescaling（归一化）。 如果输入是unit8、unit16或者二值的logical类型，则函数im2double将其值归一化0～1之间，当然就是double型的了。如果输入本身就是double类型，输出还是double类型，并不进行归一化。相当于I=double(I)/255.

（3）在图像处理中，double函数只是将读入图像的uint8数据转换为double类型，一般不使用，常用的是im2double函数，将uint8图像转为double类型，范围为0-1，如果是255的图像，那么255转为1，0还是0，中间的做相应改变。

im2double：如果输入类型是uint8、unit16 、logical，则按照0-->>0，255-->>1，将其值按比例处理成0～1之间的double数值；如果输入类型是double，输出没有处理；

mat2gray：对输入进行归一化处理，最小值-->>0;最大值-->>1，输出类型为double。

****************假设某图像数据A（uint8格式）**********************

A =235 200 89 20

>> double(A) %返回与原矩阵数值相同但类型为double的矩阵；

ans =235 200 89 20

>> im2double(A)
%返回矩阵类型：double；数值范围[0 1] ,0对应uint8中的0；1对应uint8中的255；

ans =0.9216   0.7843   0.3490   0.0784

>> mat2gray(A) %对原矩阵归一化

ans =1.0000   0.8372   0.3209    0

****************假设矩阵A为一般二维数组，非图像数据（double格式）**********************

A =   235   200   89    20

>> double(A)

ans =235   200   89   20

>> im2double(A)

ans =235   200   89   20

>> mat2gray(A)

ans =1.0000   0.8372   0.3209   0

%灰度图与彩色图的关系。

=============================================

clc

level=ones(300,300);

%显示红绿蓝三种纯色的方法。

r=cat( 3 , level*1 , level*0 , level*0 );   %纯红

g=cat( 3 , level*0 , level*1 , level*0 );  %纯绿

b=cat( 3 , level*0 , level*0 , level*1 );   %纯蓝

subplot(2,3,1) , imshow(r);

subplot(2,3,2) , imshow(g);

subplot(2,3,3) , imshow(b);

%红绿蓝三种成分随意组合会如何？

color1=cat( 3 , level*0 , level*0 , level*0 );  %纯黑

subplot(2,3,4) , imshow(color1);

color2=cat( 3 , level*1 , level*1 , level*1 );  %纯白

subplot(2,3,5) , imshow(color2);

color3=cat( 3 , level*1 , level*1 , level*0 );  %黄色

subplot(2,3,6) , imshow(color3);

更加随意组合后：

%灰度图：当RGB三通道的数值相同时，显示效果为灰度图。

A1=ones(100,100);

subplot(1 , 3 , 1)   ,  imshow(A1)

A2=ones(100 , 100)*0;

subplot(1 , 3 , 2)   , imshow(A2)

A3=ones(100 , 100)*0.5;

subplot(1 , 3 , 3)  ,  imshow(A3)

更加随意组合后：

3）用什么方法才能生成如下的3*3网格的随机彩色图？

提示：如果能把一个3*3像素的小彩图，每个像素点都膨胀n倍，不就可以达到要求了？

%%%%%%%%%%%%

clear all

k=3;             %设置网格为k*k

n=100;         %设置膨胀倍数n

rgb1=rand( k , k , 3 );

imshow(rgb1)        

%下面开始膨胀操作。

rgb=zeros( k*n , k*n , 3 );     %初始化rgb三维数组，初始值都设为0

%膨胀小图中的第一个像素...

把rgb1(1,1,3)复制100*100，放到rgb的左上角。

其他像素的操作类似..

%补齐以上代码，然后运行imshow，显示随机彩色网格图。

imshow(rgb)

%如果想查看每个通道的灰度图，则采用 imshow(rgb2(:,:,1)) imshow(rgb2(:,:,2)) imshow(rgb2(:,:,3))命令

==================================

作业1：通过学习本节的知识，编程生成一个4*4网格的随机彩色图，既共16个单元格（每个单元格子大小为100*100像素）。每次运行代码，都能得到不同颜色分布的随机图案。

作业2：（1）采用randi([1,300],[10,10])生成一个10*10的随机整数矩阵A；（2）采用逻辑索引的方法，索引出矩阵A中所有可以被3整除的元素；（3）并计算出上一步索引出的元素的总数；(4)找出A中所有不能被3整除也不能被7整除的元素的总数；（5）把A中所有可以被3整除的元素替换成0。

方法1，采用num2str函数以及字符数组的方法。

方法2，采用fix（）等函数方法。

 作业4:(1)利用randn()函数生成一个5*10的矩阵A，用ceil处理A得到矩阵x，用 floor处理A得到矩阵y，用round处理A得到矩阵z，用fix处理A得到矩阵t;

(2)计算x+y-(z+t);

拓展作业：

思考：如何改造随机彩图程序，生产类似如下的图像。下图为10*10的网格图，其中十字架形状是彩色的，其他部分是灰度图。

如果反之该如何设计？即。十字架是灰度图，其他部分是彩色的。

大家可以自己设计图案形状（如圆形、三角形、甚至阿拉伯数字）。网格的规模自己来定。