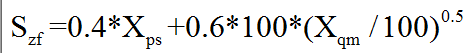%% 蒙特卡洛计算圆周率
n=1000000;
x=rand(1,n)*2-1;
y=rand(1,n)*2-1;
plot(x,y,'r*')
r=sqrt(x.^2+y.^2);
num=(r<=1);
sum(num)
mypi=sum(num)*4/n
课题练习:对数组x=randi([1,99],5,20),按行查找,把每一行第一个能被7整除的数找出来,输出该数后换行,然后停止查找该行,进入下一行继续查找。
x=randi([1,99],5,20)
[row,col]=size(x)
taget=7;
n=1;
m=1;
while n<=row
while m<=col
if rem(x(n,m),taget)==0
fprintf('In row %d ,col %d ,find the number your wanted is %d \n',n,m,x(n,m))
break
end
m=m+1;
end
m=1;
n=n+1;
end
1.11作业代码:
方法1:
clear all
k=3; %设置网格为k*k
n=100; %设置膨胀倍数n
rgb1=rand(k,k,3); %原始的k*k像素的3通道小彩图
imshow(rgb1)
%下面开始膨胀操作。
rgb=zeros( k*n , k*n , 3 ); %初始化rgb三维数组,初始值都设为0
rgb(1:100,1:100,:) =repmat(rgb1(1,1,:),100,100) ;
rgb(1:100,101:200,:)=repmat(rgb1(1,2,:),100,100) ;
rgb(1:100,201:300,:)=repmat(rgb1(1,3,:),100,100);
rgb(101:200,1:100,:) =repmat(rgb1(2,1,:),100,100);
rgb(101:200,101:200,:)=repmat(rgb1(2,2,:),100,100);
rgb(101:200,201:300,:)=repmat(rgb1(2,3,:),100,100);
rgb(201:300,1:100,:) =repmat(rgb1(3,1,:),100,100);
rgb(201:300,101:200,:)=repmat(rgb1(3,2,:),100,100);
rgb(201:300,201:300,:)=repmat(rgb1(3,3,:),100,100);
imshow(rgb)
方法2:
clear all
k=3; %设置网格为k*k
n=100; %设置膨胀倍数n
rgb1=rand(k,k,3); %原始的k*k像素的小彩图
imshow(rgb1);
%下面开始膨胀操作。
o=ones( n , n , 3 ); %初始化rgb三维数组,初始值都设为0
rgb11=o.*rgb1(1,1,:);
rgb12=o.*rgb1(1,2,:);
rgb13=o.*rgb1(1,3,:);
rgb21=o.*rgb1(2,1,:);
rgb22=o.*rgb1(2,2,:);
rgb23=o.*rgb1(2,3,:);
rgb31=o.*rgb1(3,1,:);
rgb32=o.*rgb1(3,2,:);
rgb33=o.*rgb1(3,3,:);
rgb=[rgb11,rgb12,rgb13;rgb21,rgb22,rgb23;rgb31,rgb32,rgb33];
imshow(rgb)
2.4作业水仙花问题代码:
x=100;
while x<1000
y=num2str(x);
z=str2num(y(1))^3+str2num(y(2))^3+str2num(y(3))^3;
if x==z
fprintf('%3d 是一个水仙花数字 \n',x)
end
x=x+1;
end
作业1:制作一个成绩计算程序。
(1)第1步,用input函数,让对方依次输入任意两个0-100之间的数,分别赋给变量X_ps和 X_qm。 其中变量X_ps, X_qm分别表示平时分和期末卷面分,S_zf表示总分。并判断输入的X_ps和 X_qm是否在0-100之间,如果不在,则输出警告,并要求对方重新输入正确的数值.....直到满足两个数都在0-100之间这一条件。
(2)第2步,计算总分S_zf,公式如下:
(3)第3步,采用if或者 switch语句执行以下动作:
当总分S_zf在90-100这个区间时,输出:您的平时分为:*** 卷面分为:*** 总分为:*** 成绩优秀。
当总分S_zf在70-89.9这个区间时,输出:您的平时分为:*** 卷面分为:*** 总分为:*** 成绩良好。
当总分S_zf在60-69.9这个区间时,输出:您的平时分为:*** 卷面分为:*** 总分为:*** 成绩及格。
当总分S_zf在0-59.9这个区间时,输出: 您的平时分为:*** 卷面分为:*** 总分为:*** 等着补考吧。
(提示:需要用到while循环、 if或者 switch分支,fprintf格式输出,数值的大于、小于、与或非等逻辑判断语句。)
% 采用if或者 switch语句制作一个成绩计算程序
X_ps=input('请输入你的平时分:');
X_qm=input('请输入你的期末考试分:');
while X_ps>100 | X_ps<0 | X_qm>100 | X_qm<0
fprintf('输入有误,输入的分数应该在0-100之间 \n');
X_ps=input('请输入你的平时分:');
X_qm=input('请输入你的期末考试分:');
end
S_zf=0.4*X_ps+0.6*100*(X_qm/100)^0.5;
if S_zf>=90
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩优秀. \n' ,X_ps,X_qm, S_zf);
elseif S_zf>=70&S_zf<90
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩良好. \n',X_ps,X_qm, S_zf);
elseif S_zf>=60&S_zf<70
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩及格. \n',X_ps,X_qm, S_zf);
elseif S_zf<60
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 等着补考吧. \n',X_ps,X_qm, S_zf);
end
%%%=======================================================
作业2:用while循环求解e的值。
把x=1带入上式,就可以得到e的值,计算的项数越多,则精度越高。
任务1:编程计算e的值,要求当最后一项的值1^n/n!<0.000001时结束计算,并输出此时算出的e值。
任务2 : 已知e^2的精确值为 exp(2)=7.3890560989306504069418224389,编程求解n多大的时候,才能让所计算出来的近似的e^2值精确到小数点后10位,也就是小数点之后的前10位都是正确的?提示:如果要求计算出的e^2的值精确到小数点后10位,则其和真实的exp(2)之间的差要小于0.0000000001.
提示,编程时可能会用到阶乘,MATLAB里阶乘的函数为 factorial( )
如12的阶乘:
factorial(12) % 12的阶乘已经很大了
ans =
479001600
====================================
%任务1
e=1;
n_v=1;
n=1;
while n_v>0.000001
n_v=1/factorial(n);
e=e+n_v;
n=n+1;
end
e
%任务2
e2=1;
n_v=0;
n=1;
while abs(e2-7.38905609893)>0.00000000001
n_v=(2^n)/factorial(n);
e2=e2+n_v;
n=n+1;
end
e2
n-1
作业3:求100-999之间的全部水仙花数。
水仙花数是指:一个三位数,其各位数字立方和等于该数本身。例如:370=33+73+03.这就说明370是一个水仙花数。
%水仙花数,向量化编程
x=100:999;
x=x'
y=num2str(x)
x1=str2num(y(:,3))
x10=str2num(y(:,2))
x100=str2num(y(:,1))
v=find(x==(x1.^3+x10.^3+x100.^3))
v=v+100-1
当你输入信用卡号码的时候,有没有担心输错了而造成损失呢?其实可以不必这么担心,因为并不是一个随便的信用卡号码都是合法的,它必须通过Luhn算法来验证通过。
该校验的过程:
1、从卡号最后一位数字开始,逆向将奇数位(1、3、5等等)相加。
2、从卡号最后一位数字开始,逆向将偶数位数字,先乘以2(如果乘积为两位数,则将其减去9),再求和。
3、将奇数位总和加上偶数位总和,结果应该可以被10整除。
例如,卡号是:5432123456788881
逆向奇数位为 4 2 2 4 6 8 8 1 和 = 35
逆向偶数位乘以2(有些要减去9)的结果:1 6 2 6 1 5 7 7,求和 = 35。
最后 35 + 35 = 70 可以被10整除,认定校验通过。
请编写一个程序,从标准输入获得卡号,然后判断是否校验通过。通过显示:“成功”,否则显示“失败”。
比如,输入:356827027232780 程序输出:成功
x=input('请输入卡号,并以单引号引住这串数字:')
L=length(x)
y=x([L:-1:1])
s_even=0;
s_odd=0;
for n=1:2:L
t1=str2num(y(n));
s_odd=s_odd+t1;
end
for n=2:2:L
t2=str2num(y(n));
if t2*2>9
k=t2*2-9;
else
k=t2*2;
end
s_even=s_even+k;
end
total=(s_odd+s_even)
if mod(total,10)==0
fprintf('卡号正确 \n');
else
fprintf('卡号错误 \n');
end
===========================================================
作业1:设计一个函数mymaxmin(A),调用此函数可以返回矩阵(或者数组)中最大值以及最小值元素和平均值等。
输入参数A为输入的一个矩阵或者数组。
返回参数ma,mi为找到的矩阵A中的最大值与最小值。
返回参数ma,mi,ma_R,ma_C,mi_R,mi_C为最大值与最小值所对应的行号和列号。
返回参数pjz为矩阵A中的平均值。
要求:不能用matlab自带的max/min等现成的函数,要自己用for循环、if判断、>=,等方式寻找最大与最小值。
function [ma,mi,ma_R,ma_C,mi_R,mi_C,pjz] = mymaxmin(A)
%此函数的功能是找到矩阵中的最大值及最小值,以及这两个最值对应的坐标。
[m,n]=size(A);
ma=-inf;
mi=inf;
pjz=0;
for k=1:m
for t=1:n
if A(k,t)>ma
ma=A(k,t);
ma_R=k;
ma_C=t;
end
if A(k,t)<mi
mi=A(k,t);
mi_R=k;
mi_C=t;
end
pjz=pjz+A(k,t);
end
end
pjz=pjz/(m*n);
end
==========================================================
作业2:试着看看能否自己设计一个函数,比如命名为myfind.m, 实现matlab自带的find函数的类似功能?
输入参数A为输入的一个矩阵或者数组。
输入参数W只能为1或者0;k=1时找到矩阵A中的大于等于k的所有元素,k=0时找到矩阵A中的小于等于k的所有元素。
返回参数 A_k , A_k_R , A_k_C为3个数组,分别记录按照要求找到的元素,以及这些元素对应的行号和列号 。
要求:
(1)不能用matlab自带的find等现成的函数,要自己用for循环、if判断、>=,等方式寻找最大与最小值。
(2)如果对方输入的参数w 不是0或者1,则要求对方重新输入正确的值。
(3)如果没有找人任何符合要求的元素,则打印输出一句话“很抱歉,没有找到符合条件的元素。”
function [ A_k , A_k_R , A_k_C ] = myfind(A , k , w )
%此函数的功能是找到矩阵A中的大于k(当W=1时),或者小于k(当W=0时)的元素。
while ( w~=0)&( w~=1)
fprintf('输入有误,w的值必须是0或者1 \n');
w =input('请重新输入 w =');
end
[m,n]=size(A);
A_k=[];
if w==1
fprintf('即将为您寻找矩阵%c %c %f 的所有元素。 \n' ,'A' ,'>',k);
Num=0;
for ii=1:m
for jj=1:n
if A(ii,jj)>=k
Num=Num+1;
A_k(Num)=A(ii,jj);
A_k_R(Num)=ii;
A_k_C(Num)=jj;
end
end
end
end
if w==0
fprintf('即将为您寻找矩阵%c %c %f 的所有元素。 \n' ,'A' ,'<',k);
Num=0;
for ii=1:m
for jj=1:n
if A(ii,jj)<=k
Num=Num+1;
A_k(Num)=A(ii,jj);
A_k_R(Num)=ii;
A_k_C(Num)=jj;
end
end
end
end
end
===============================================================
采用子函数方式,制作一个成绩查询程序
function chengji(x1,x2)
% 采用if或者 switch语句制作一个成绩计算程序,输入平时成绩和期末卷面成绩,将计算总成绩,并输出。
%
%chengji(x1,x2) 中,第一个参数x1为平时成绩,第二个参数x2为期末成绩
%
%用三个子函数,分别实现:分数检测、总分的计算、输出
[X_ps,X_qm]=jiance(x1,x2);
S_zf=jisuanzf(X_ps,X_qm);
shuchu(X_ps , X_qm , S_zf);
end
function [X_ps,X_qm]=jiance(x1,x2)
%子程序,负责检查输入是否有错
X_ps=x1;
X_qm=x2;
while X_ps>100 | X_ps<0 | X_qm>100 | X_qm<0
fprintf('输入有误,输入的分数应该在0-100之间 \n');
X_ps=input('请重新输入你的 , 平时分:');
X_qm=input('请重新输入你的 , 期末考试分:');
end
end
function S_zf=jisuanzf(x1,x2)
%子程序,负责计算总分
X_ps=x1;
X_qm=x2;
S_zf=0.4*X_ps+0.6*100*(X_qm/100)^0.5;
end
function shuchu(x1,x2,x3)
%子程序,负责打印输出
X_ps=x1;
X_qm=x2;
S_zf=x3;
if S_zf>=90
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩优秀. \n' ,X_ps ,X_qm , S_zf);
elseif S_zf>=70&S_zf<90
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩良好. \n',X_ps ,X_qm , S_zf);
elseif S_zf>=60&S_zf<70
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 成绩及格. \n',X_ps ,X_qm , S_zf);
elseif S_zf<60
fprintf('您的平时分为:%5.2f 卷面分为:%5.2f 总分为:%5.2f 等着补考吧...... \n',X_ps ,X_qm , S_zf);
end
end
傅里叶变换
==========================================
%% 离散傅里叶变换DFT Cui chun lei 20200318
clear all
n=10
y=rand(1,n) %生成随机序列
tic %计时器
f_FFT=fft(y);
t_fft=toc;
tic
f_myDFT=zeros(1,n);
for f=0:n-1
for ii=0:n-1
f_myDFT(f+1)=f_myDFT(f+1)+y(ii+1)*exp(-i*2*pi*f*ii/n)*1 ;
%ii/n 为时间增长,范围从0/n到(n-1)/n,为什么没有到n/n?是因为dft过程实际是不停用不同频率的正弦(余弦)去和被测函数y进行相乘,然后把结果累积起来。
%而一个正弦函数是连续的,不可能取无穷多个点,所以实际操作时,在一个周期内选n个点,用这n个点对应的正弦值去和被测函数y进行相乘,从第0个点开始,到第n-1.共n个。
%其实第n个点就是下一个周期的第一个点,所以只需要到(n-1)/n
end
end
t_myDFT=toc;
f_FFT %MAT自带FFT算法
t_fft %自带算法耗费时间
f_myDFT %自己设计的DFT算法
t_myDFT %自己设计的算法耗费时间
%% 自己设计的算法的应用==================================
clear all
t_s=0;
t_e=5;
t_D=0.001;
f_Limit=1/t_D;
t=[t_s: t_D :t_e];
n=(t_e-t_s)/t_D+1; %共(t_e-t_s)/t_D +1个采样点
%y=sin(2*pi*70*t)+randn(1,n)*0.3; %加个随机噪声
y=sin(2*pi*30*t).*cos(2*pi*300*t)+randn(1,n)*0.01;
%y=sin(2*pi*10*t.^2)+randn(1,n)*0.1;
tic
f_FFT=fft(y);
t_fft=toc;
tic
f_myDFT=zeros(1,n);
for f=0:n-1
for ii=0:n-1
f_myDFT(f+1)=f_myDFT(f+1)+y(ii+1)*exp(-i*2*pi*f*ii/n)*1 ;
%ii/n 为时间增长,范围从0/n到(n-1)/n,为什么没有到n/n?是因为dft过程实际是不停用不同频率的正弦(余弦)去和被测函数y进行相乘,然后把结果累积起来。
%而一个正弦函数是连续的,不可能取无穷多个点,所以实际操作时,在一个周期内选n个点,用这n个点对应的正弦值去和被测函数y进行相乘,从第0个点开始,到第n-1.共n个。
%其实第n个点就是下一个周期的第一个点,所以只需要到(n-1)/n
end
end
t_myDFT=toc;
f_FFT
t_fft
f_myDFT
t_myDFT
f_FFT_v=abs(f_FFT);
f_FFT_v=fftshift(f_FFT_v);
f_myDFT_v=abs(f_myDFT);
f_myDFT_v=fftshift(f_myDFT_v);
f_D=f_Limit/(n-1);
f=[0: f_D :f_Limit];
f=f-f_Limit/2;
subplot(3,1,1); plot(f,f_FFT_v); title('FFT');
subplot(3,1,2); plot(f,f_myDFT_v); title('my DFT');
subplot(3,1,3); plot(t,y); title('原始信号y');
%% 二维DFT=============================================
%% 自己设计的二维DFT算法,cuichunlei 20200319
clear all
pic=imread(' F:\bird_gray_small.jpg ');
[m,n]=size(pic)
% pic=rand(5,5)
% [m,n]=size(pic)
tic %计时器
f_FFT=fft2(pic);
t_fft=toc;
pic=double(pic);
f_myDFT=zeros(m,n);
tic
for u=0:m-1
if rem(u,10)==0
u
end
for x=0:m-1
for v=0:n-1
for y=0:n-1
f_myDFT(u+1,v+1)=f_myDFT(u+1,v+1)+pic(x+1,y+1)*exp(-i*2*pi*u*x/m-i*2*pi*v*y/n)*1 ;
end
end
end
end
t_myDFT=toc;
f_FFT;
t_fft
f_myDFT;
t_myDFT
f_FFT=fftshift(f_FFT);
f_FFT_v=abs(f_FFT);
f_FFT_v=mapminmax(f_FFT_v,0,1);
f_myDFT=fftshift(f_myDFT);
f_myDFT_v=abs(f_myDFT);
f_myDFT_v=mapminmax(f_myDFT_v,0,1);
subplot(2,2,1); imshow(f_FFT_v); title('FFT');
subplot(2,2,2); imshow(f_myDFT_v); title('my DFT');
pic2=imread(' F:\bird_gray.jpg '); %读取原始大图
f_FFT2=fft2(pic2);
f_FFT2=fftshift(f_FFT2);
F=abs(f_FFT2);
F=mapminmax(F,0,1);
subplot(2,2,3); imshow(pic2); title('原始大图');
subplot(2,2,4); imshow(F); title('原始大图FFT');
%% 参考别人的代码=========================================
clear all;
N=256;
dt=0.02;
n=0:N-1;
t=n*dt;
x=sin(2*pi*t);
m=N;
a=zeros(1,m);
b=zeros(1,m);
for k=0:m-1
for y=0:N-1
a(k+1)=a(k+1)+2/N*x(y+1)*cos(2*pi*k*y/N);
b(k+1)=b(k+1)+2/N*x(y+1)*sin(2*pi*k*y/N);
end
c(k+1)=sqrt(a(k+1)^2+b(k+1)^2);
end
subplot(211); plot(t,x); title('原始信号'), xlabel('时间/t');
f=(0:m-1)/(N*dt);
subplot(212);plot(f,c);hold on
title('Fourier');xlabel('频率/HZ');ylabel('振幅');
ind=find(c==max(c),1,'first');%寻找最大值的位置
%%%%%%% ind = find(X, k) 或ind = find(X, k, 'first')
% 返回第一个非零元素k的索引值(顺序)。
% k必须是一个正数,但是它可以是任何数字数值类型。
x0=f(ind); %根据位置得到横坐标(频率)
y0=c(ind); %根据位置得到纵坐标(幅度)
plot(x0,y0,'ro');hold off
%%%%%%% hold on 和hold off,是相对使用的.通常是一个图上画两个曲线进行比较。
% 前者的意思是,你在当前图的轴(坐标系)中画了一幅图,再画另一幅图时,原来的图还在,与新图共存,都看得到
% 后者表达的是,你在当前图的轴(坐标系)中画了一幅图,此时,状态是hold off,则再画另一幅图时,原来的图就看不到了,在轴上绘制的是新图,原图被替换了
text(x0+1,y0-0.1,num2str(x0,'频率=%f'));
% text(x,y,'string')在图形中指定的位置(x,y)上显示字符串string
====================================
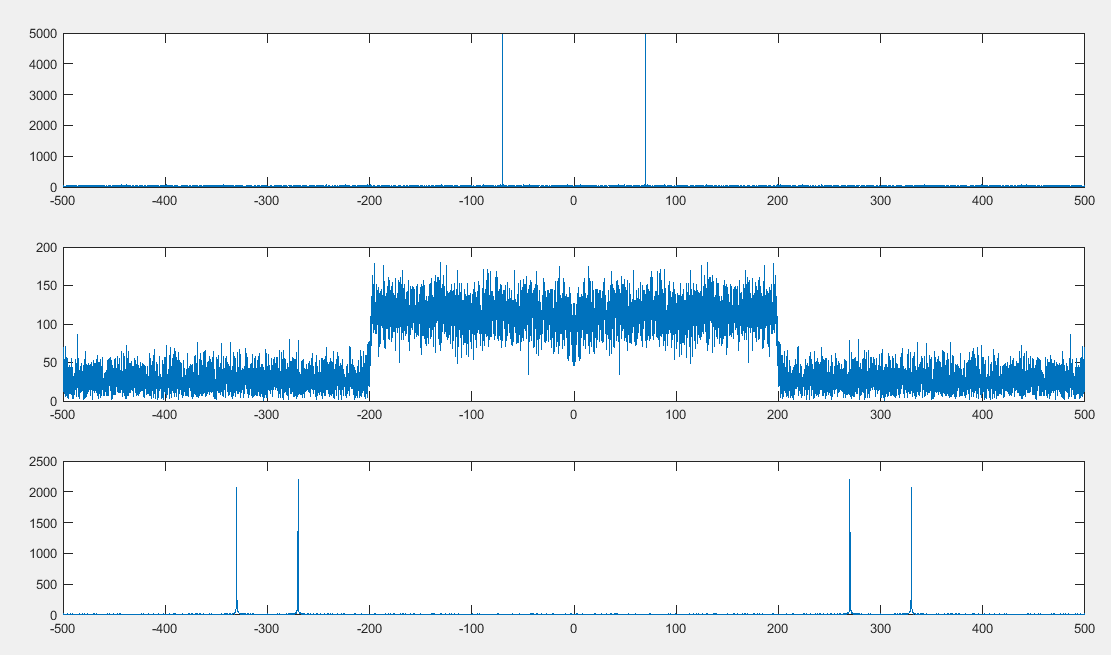
%fft变换
t_s=0;
t_e=10;
t_D=0.001;
f_Limit=1/t_D;
t=[t_s:t_D:t_e];
N=(t_e-t_s)/t_D+1; %共(t_e-t_s)/t_D +1个采样点
y1=sin(2*pi*70*t)+randn(1,N)*0.3; %加个随机噪声
y2=sin(2*pi*10*t.^2)+randn(1,N)*0.3; %加个随机噪声
y3=sin(2*pi*30*t).*cos(2*pi*300*t)+randn(1,N)*0.1; %加个随机噪声
F1=abs(fft(y1));
F2=abs(fft(y2));
F3=abs(fft(y3));
F1=fftshift(F1);
F2=fftshift(F2);
F3=fftshift(F3);
f_D=f_Limit/(N-1);
f=[0:f_D:f_Limit];
f=f-f_Limit/2;
subplot(3,1,1);plot(f,F1)
subplot(3,1,2);plot(f,F2)
subplot(3,1,3);plot(f,F3)
%% 二维傅里叶逆变换
x=imread('F:\bird_gray.jpg'); %读入灰度图
y=fft2(x); %二维傅里叶变换
z=ifft2(y)/255; %二维傅里叶逆变换
subplot(2,1,1);imshow(x);
subplot(2,1,2);imshow(z);
%% 二维傅里叶逆变换 用于滤波
I=imread('F:\bird_gray.jpg');
figure(1);
imshow(I);
J=imnoise(I,'gaussian',0,0.02);
figure(2);
imshow(J);
J=double(J);
f=fft2(J); %采用傅里叶变换
g=fftshift(f); %数据局陈平衡
[M,N]=size(f);
n1=floor(M/2); %滤波半径
n2=floor(N/2);
d0=10;
for i=1:M
for j=1:N
d=sqrt((i-n1)^2+(j-n2)^2);
if d>=d0
h1=1;
h2=1+0.5;
else
h1=0;
h2=0.5;
end
g1(i,j)=h1*g(i,j);
g2(i,j)=h2*g(i,j);
end
end
g1=ifftshift(g1);
g1=uint8(real(ifft2(g1))); %显示理想高通滤波结果
figure(3);imshow(g1);
title('理想高通滤波结果')
g2=ifftshift(g2);
g2=uint8(real(ifft2(g2)));
figure(4);imshow(g2); %显示理想高通加强滤波结果
title('理想高通加强滤波结果')
排序算法:
A=input('请输入一个数组:')
n=length(A); %测量输入数组A的长度
for ii=1:n-1 % ii表示趟数
for jj=1:n-ii % 开始两两比较,n-ii表示每一趟内部需要进行的两两比较的总数目
if A(jj)>=A(jj+1) %如果左边元素大于右边元素,则交换两者位置。
p=A(jj);
A(jj)=A(jj+1);
A(jj+1)=p;
end
end
end
A %显示结果
冒泡排序算法的函数化:
function B = mysort(A , order)
%这是一个冒泡排序算法,对输入的数组A进行排序
%order=1,表示按照从小到大进行排序,如果order=0,则从大到小排序
n=length(A); %测量输入数组A的长度
if order==1 %参数order为1则按升序排序
for ii=1:n-1 % ii表示趟数
for jj=1:n-ii % 开始两两比较,n-ii表示每一趟内部需要进行的两两比较的总数目
if A(jj)>=A(jj+1) %如果左边元素大于右边元素,则交换两者位置。
p=A(jj);
A(jj)=A(jj+1);
A(jj+1)=p;
end
end
end
end
if order==0 %参数order为0则按降序排序
for ii=1:n-1 % ii表示趟数
for jj=n:-1:ii+1 % 开始两两比较
if A(jj)>=A(jj-1) %如果左边元素大于右边元素,则交换两者位置。
p=A(jj);
A(jj)=A(jj-1);
A(jj-1)=p;
end
end
end
end
B = A; %把最终得到的A,赋给B。B就是函数返回的按照要求排序好的数组。
end
%插入排序法,方法1(最优)
clc
clear all
%a=[3,1,5,12,7,0,17,9,4,33,22,19,-7,31,-2,25,15,3]; %待排序数列
%a=input('请输入数组a:')
a=randi([-100,100],1,50)
b=[]; %表示已经排好序的数列,暂时为空
b(1)=a(1); %先把第一个元素归类到已排好的序列内
n=length(a);
for i=2:n %则数组A里从2-n的为待排序数列
if a(i)>b(i-1)
%如果a中被排序的第i个元素比已经排好序序列内的最后一个元素都小,那就直接把a中第i个元素复制到b中第i个元素.否则进行else中的逐个比较过程;
b(i)=a(i);
else
for j=1:i-1 %把a中待排序的第i个元素和已经排好序序列内的元素逐个比较大小
if a(i)<=b(j)
%如果a中被排序的第i个元素比已经排好序序列内的第j个元素小,则把a中第i个元素插入b中的第j个位置,原来b中从j到尾巴的所有元素整体后移一位
b(j+1:i)=b(j:i-1);
b(j)=a(i);
break %这个break很重要。
end
end
end
end
b
===================================================================
%插入排序法,方法2(不是最优,但是好理解)
clear all
clc
a=[3,1,5,12,7,0,17,9,4,33,22,19,-7,31,-2]; %待排序数列
b=zeros(1,12); %表示已经排好序的数列,暂时为空
b(1)=a(1); %先把第一个元素归类到已排好的序列内
n=length(a);
for i=2:n %则数组A里从2-n的为待排序数列
for j=1:i-1 %把a中待排序的第i个元素和已经排好序序列内的元素逐个比较大小
if a(i)<=b(j)
%如果a中被排序的第i个元素比已经排好序序列内的第j个元素小,则把a中第i个元素插入b中的第j个位置,原来b中从j到尾巴的所有元素整体后移一位
b(j+1:i)=b(j:i-1);
b(j)=a(i);
break %这个break很重要。
end
end
if a(i)>b(i-1) %如果
b(i)=a(i);
end
end
b
===========================================
%选择排序
clc
clear all
a=[3,1,5,12,7,0,17,9,4,33,22,19,-7,31,-2,25,15,3]; %待排序数列
%a=randn(1,50)
b=a; %
n=length(a);
for j=1:n-1
min_temp=b(j);
k=j;
for i=j+1:n %
if b(i)<min_temp
min_temp=b(i);
k=i;
end
end
if k>j
tmp=b(j);
b(j)=b(k);
b(k)=tmp;
end
end
b
======================================
画图找根:0=x1.^3+14*x1.^2-4*x1-30;
x1=[-16:0.001:12];
y1=x1.^3+14*x1.^2-4*x1-30;
plot(x1,y1, '-r')
grid on
求和:S=1*2*3+2*3*4+………+50*51*52
s=0;
for i=1:50
s=i*(i+1)*(i+2)+s;
end
s
求方程sin(2*x)-exp(x/5)+1.2=0 在-10到+10之间的解。
x=linspace(-10,10,500000);
y= sin(x*2)- exp(x/5)+1.2;
plot(x,y,'b');
grid on
1.编程,求圆周率Pi中前100万位里,是否出现你的生日(六位生日,如1999年3月1日,则认为生日为 990312),如果出现则具体出现了多少次,分别出现是小数点后的多少位?
clc
str1='990312' %要找的字符串
n=length(str1); %测量这个字符串的长度
pi_str=char(vpa(pi,100000)); %把pi显示100000位后,再转换为字符串
M=length(pi_str); % 测量这个字符串的长度
count=0; %计数器,用来记录找到了多少次符合条件的情况
for i=3:M-n %从字符串第三位开始寻找,因为前两位为: 3.
if pi_str( i : (i+n-1) )==str1
count=count+1; %若if成立,则说明找到了符合要求的。计数器加1
fprintf('第%d次找到符合条件,其在小数点后%d 位 \n' ,count , (i-2) )
end
end
fprintf(' \n 所搜索的字符串在pi里共出现了%d次 \n' ,count )
=================================
还可以用findstr函数,查找字符串中的子串。
例:
>>str='ancdr'
>>findstr (str,'dr')
ans =
4

strcat函数的作用:连接两个字符串。
例:
s1='I' ;s2=', ' ;s3='L' ;s4='o' ;s5='v';
s6='e' ;s7=', ' ;s8='y' ;s9='o' ;s10='u';
s=strcat(s1,s2,s3,s4,s5,s6,s7,s8,s9,s10)
2.某个数的三次方是4位数,四次方是6位数,且其三次方和四次方这两个数正好把0-9这10个数字用完,不多不少,求这个数是多少?
分析:
(1)4位数区间为:1000-9999,开3次方为:10-21.5436,取10-21
(2)6位数区间为:100000-999999,开4次方为:17.7828-31.6228,取18-31
由上可知:这个数位于18-21之间
clc
for i=18:21
x=num2str(i^3) %把数字转为字符串
y=num2str(i^4) %把数字转为字符串
z=strcat(x,y) %通过strcat函数合并两个字符串
z=sort(z) %对这个字符串从小到大排序
if z=='0123456789'
fprintf('找到符合条件的I=%d, 其3次方为%d,4次方为%d \n' , i , i^3 ,i^4 )
break
end
end
作业1:思考一下,如何才能输出类似如下的乘法口诀表?
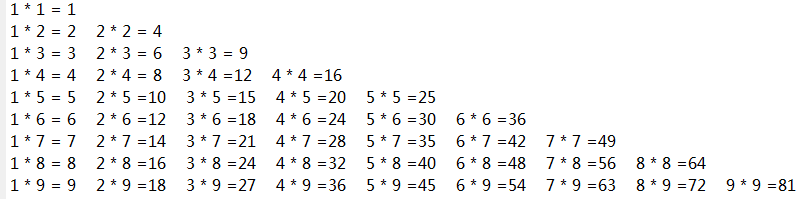
for n=1:9
for m=1:n
fprintf('%d * %d =%2d ',m,n,n*m)
end
fprintf('\n')
end3.编程找出1000之内所有的勾股数。
满足 x^2+y^2=z^2 的一组正整数(x, y , z)称为一组勾股数。
如:3,4,5
% 编程找出1000之内所有的勾股数。
N=1000;
num=0;
for z=5:N
for y=1:z-1
for x=1:y-1
if x^2+y^2==z^2
num=num+1;
fprintf('x=%3d , y=%3d , z=%3d \n' ,x,y,z)
end
end
end
end
num
作业2:给一个无限长的自然数构成的字符串
S: 12345678910 111213141516171819 202122232425….....,
它是由所有自然数从小到大依次排列起来的,任意给一个数字串S1(如751),编程求出它第一次出现的位置。
% 给一个无限长的自然数构成的字符串
% S: 12345678910 111213141516171819 202122232425….....,
% 它是由所有自然数从小到大依次排列起来的,任意给一个数字串S1(如7518),
% 编程求出它第一次出现的位置。
clc
str1='751' %要找的字符串
n=length(str1); %测量这个字符串的长度
S=[];
S=char(x);
K=1;
for i=1:5000 %先生成这个字符串
L=length(num2str(i));
S(K:K+L-1)=num2str(i);
K=K+L;
end
M=length(S)
for i=1:M-n+1
if S(i : i+n-1)==str1
fprintf('你想找的这个数,第一次出现在s序列的第%d位 \n' , i )
break
end
end
5.求1000之内所有的素数。
clear
N=1000;
X=1:N; %求N之内的素数
tag([1:N])=NaN; %设置一个标签数组,初始化为nan
tag(1)=0; %用0标识这个位置对于的x的值为合数
tag(2)=1; %用1标识这个位置对于的x的值为素数
for k=2:N
m=fix(sqrt(k))+1; %只需判断到 fix(sqrt(k))+1
for i=2:m
if tag(k)==0 %如果某个数x对于的tag标识为0,则跳出循环
break
end
if mod(X(k),i)==0 %如果能被整除,则tag标识为0,跳出循环
tag(k)=0;
break
end
end
if i==m %如果i==m,说明K是素数
tag(k)=1; %则tag标识为1
d=2; %此时k的倍数(2-inf倍)肯定都是合数, tag都要标记为0
while k*d<=N
tag(k*d)=0;
d=d+1;
end
end
end
p=X(tag==1) %把TAG所有是1的位置索引出来,既素数
p_num=length(p) %本代码计算出来的N之内的素数个数
length(primes(N)) %matlab内置函数计算出来的素数个数
clear all
N=input('请输入 N= '); %求整数N之内的素数;
disp('N以内全体素数:')
count=0;
for i=2:N
j=2; % 每次外循环,j都要从头再来,所以要拿到外循环里。
k=sqrt(i);
while j
if rem(i,j)==0
break % 说明I是一个合数,不用再继续算下去了。
else
j=j+1;
end
if j>k % 到目前位置I都不是合数,说明I必定是素数。
fprintf('%8d',i) % 要不都挨一块分不出个儿来了。
count=count+1;
if rem(count,10)==0
%这个if块,要放到判断j>k里,要不会多出好多空行
fprintf('\n')
end
break
% 这个最重要,j>k时一定要退出内循环,要不然j会继续运行到等于i才会退出的
end
end
end
%% 素数问题
%素数定理
%高斯引入的素数计数函数 π(x) 就是做这件事的,它会给出小于或等于一个给定实数的素数的数量
% 素数定理:“当x增长到无穷大时,素数计数函数 π(x) 会近似于 x/ln(x) 函数。
% 换句话说,若你的计数足够大,且将素数数量的图绘制到一个非常大的数 x,接着绘制 x 除以 x 的自然对数,
% 二者会临近相同的值。
% https://zhuanlan.zhihu.com/p/25055731
clc
clear all
N=3000;
x=[2:N];
for k=2:N
p_n(k-1)=length(primes(k));
end
plot(x,p_n,'r')
hold on
y=x./log(x);
plot(x,y,'k')
hold on
for k=2:N
f = @(x) 1./log(x);
li(k-1)=quadl(f,2,k);
end
plot(x,li,'b')
grid on
%% 素数问题的函数化编程
%功能:返回N1之内两个素数P,Q,使得P/Q尽量接近PI
function [p,q,loss]=pi_prim(N1)
while N1<2
fprintf('输入有误,输入的两个数字应该大于等于2 \n');
N1=input('请重新输入N1=');
end
N=ceil(N1) ;
pri=M_prim(2,N);
n=length(pri)
loss=100;
for ii=5:n
x1=ceil(pri(ii)/4);
x2=ceil(pri(ii)/3);
pri_x1=M_prim(2,x1);
pri_x2=M_prim(2,x2);
m=length(pri_x2)-length(pri_x1);
if m>=1
for jj=1:m
mypi=pri(ii)/pri(length(pri_x1)+jj);
if loss>abs(mypi-pi)
loss=abs(mypi-pi);
p=pri(ii);
q=pri(length(pri_x1)+jj);
fprintf('loss is :%.20f , prime1 is : %d , prime2 is : %d \n', loss , pri(ii) ,pri(length(pri_x1)+jj) );
%转义序列 %.20f代表小数点后有20位小数。
fprintf('\n')
end
end
end
end
end
function M= M_prim(N1,N2)
while N1<2 | N2<2
fprintf('输入有误,输入的两个数字应该大于等于2 \n');
N1=input('请重新输入N1=');
N2=input('请重新输入N2=');
end
M=[];
num=0;
m1=floor( min(N1,N2) );
m2=ceil( max(N1,N2) );
for k=m1:m2
if is_prim(k)==1
num=num+1;
M(num)=k;
end
end
end
function v= is_prim(A)
while A<2
fprintf('输入有误,输入的数字应该大于等于2 \n');
A=input('请重新输入一个大于等于2的正整数:');
end
n=ceil( sqrt(A) );
v=1;
if A>2
for ii=2:n
if rem(A,ii)==0
v=0;
% fprintf('%d不是素数,因为%d = %d * %d \n',A,A,ii,A/ii);
break
end
end
end
if v==1
% fprintf('%d是素数 ! \n',A);
end
end
%功能:画出N1之内的素数计数函数的图像
function plot_prim(N1)
while N1<2
fprintf('输入有误,输入的两个数字应该大于等于2 \n');
N1=input('请重新输入N1=');
end
N=ceil(N1) ;
x=[2:N];
for k=2:N
p_n(k-1)=length(M_prim(2,k));
end
plot(x,p_n,'r')
hold on
y=x./log(x);
plot(x,y,'k')
hold on
for k=2:N
f = @(x) 1./log(x);
li(k-1)=quadl(f,2,k);
end
plot(x,li,'b')
grid on
end
function M= M_prim(N1,N2)
while N1<2 | N2<2
fprintf('输入有误,输入的两个数字应该大于等于2 \n');
N1=input('请重新输入N1=');
N2=input('请重新输入N2=');
end
M=[];
num=0;
m1=floor( min(N1,N2) );
m2=ceil( max(N1,N2) );
for k=m1:m2
if is_prim(k)==1
num=num+1;
M(num)=k;
end
end
end
function v= is_prim(A)
while A<2
fprintf('输入有误,输入的数字应该大于等于2 \n');
A=input('请重新输入一个大于等于2的正整数:');
end
n=ceil( sqrt(A) );
v=1;
if A>2
for ii=2:n
if rem(A,ii)==0
v=0;
% fprintf('%d不是素数,因为%d = %d * %d \n',A,A,ii,A/ii);
break
end
end
end
if v==1
% fprintf('%d是素数 ! \n',A);
end
end
%功能:返回一个数组或者元胞数组,包含N1-N2之间的所有孪生素数
function [Twin_M,Twin_cell]= Twin_prim(N1,N2)
while N1<2 | N2<2
fprintf('输入有误,输入的两个数字应该大于等于2 \n');
N1=input('请重新输入N1=');
N2=input('请重新输入N2=');
end
Twin_M=[];
Twin_cell={};
num=0;
m1=floor( min(N1,N2) );
m2=ceil( max(N1,N2) );
M= M_prim(m1,m2);
L=length(M);
for ii=1:L-1
if M(ii+1)-M(ii)==2
num=num+1;
Twin_M(: ,num)=[M(ii),M(ii+1)]';
Twin_cell{1,num}=[M(ii),M(ii+1)];
end
end
end
function M= M_prim(N1,N2)
M=[ ];
num=0;
m1=floor( min(N1,N2) );
m2=ceil( max(N1,N2) );
for k=m1:m2
if is_prim(k)==1
num=num+1;
M(num)=k;
end
end
end
function v= is_prim(A)
while A<2
fprintf('输入有误,输入的数字应该大于等于2 \n');
A=input('请重新输入一个大于等于2的正整数:');
end
n=ceil( sqrt(A) );
v=1;
if A>2
for ii=2:n
if rem(A,ii)==0
v=0;
break
end
end
end
if v==1
end
end
%功能:返回一个数值M,存储着N1,N2之间的所有素数。
function M= M_prim(N1,N2)
while N1<2 | N2<2
fprintf('输入有误,输入的两个数字应该大于等于2 \n');
N1=input('请重新输入N1=');
N2=input('请重新输入N2=');
end
M=[];
num=0;
m1=floor( min(N1,N2) );
m2=ceil( max(N1,N2) );
for k=m1:m2
if is_prim(k)==1
num=num+1;
M(num)=k;
end
end
end
function v= is_prim(A)
while A<2
fprintf('输入有误,输入的数字应该大于等于2 \n');
A=input('请重新输入一个大于等于2的正整数:');
end
n=ceil( sqrt(A) );
v=1;
if A>2
for ii=2:n
if rem(A,ii)==0
v=0;
break
end
end
end
if v==1
end
end
%功能:判断是否是素数,是的话返回1,否则返回0
function v= is_prim(A)
while A<2
fprintf('输入有误,输入的数字应该大于等于2 \n');
A=input('请重新输入一个大于等于2的正整数:');
end
n=ceil( sqrt(A) );
v=1;
if A>2
for ii=2:n
if rem(A,ii)==0
v=0;
fprintf('%d不是素数,因为%d = %d * %d \n',A,A,ii,A/ii);
break
end
end
end
if v==1
fprintf('%d是素数 ! \n',A);
end
end
3X+1猜想:
%版权:gdcp_ccl_20210601
clear all
N=input('input='); %比如6171
N=abs( fix(N) ); %或者: N=uint32(N) ; 防止有人输入的数有小数点,或者是负数。
m=[]; %用数组m来存储3x+1序列中的各个数
k=1; %k表示数组m的下标,初始值为1
m(k)=N; %显然,数组m中的第一个元素为N
%生成3x+1序列
while m(k)~=1 %如果数组m中当前元素不为1,则继续,否则停止计算
if mod(m(k),2)~=0 %如果当前元素为奇数,则乘三加一
m(k+1)=3*m(k)+1;
else %如果当前元素为偶数,则除2
m(k+1)=m(k)/2;
end
k=k+1; %下标加1,把下一个元素当成“当前”元素。
end
%计算3x+1序列中的长度,最大值,最大值和输入值之间的比例
L=numel(m);
m_max=max(m);
Ratio=m_max/N;
%输出3x+1序列,每行10个
for k=1:L
fprintf('%8d',m(k))
if mod(k,10)==0 %每输出10个,回车一次
fprintf('\n')
end
end
fprintf('\n')
%输出3x+1序列的相关参数
fprintf('数字%d的3x+1序列长度 = %d \n', N,L );
fprintf('数字%d的3x+1序列中的最大值 = %d \n', N,m_max );
fprintf('数字%d的3x+1序列中的最大值与初始值的比值为 = %d \n', N,Ratio );
plot(m,'*-') %画出该数字的3x+1序列的图
for n=1:9
for m=1:n
fprintf('%d * %d =%d ',n,m,n*m)
end
fprintf('\n')
end某个数的三次方是4位数,四次方是6位数,且其三次方和四次方这两个数正好把0-9这10个数字用完,不多不少,求这个数是多少?
把直角坐标系,按逆时针等间隔发射10条射线;第一条射线为X轴正方向,用数字“0”代表,依次类推(相邻两个射线夹角36度)画出其他九条射线;假设一个点从原点出发,以圆周率PI小数点后的数字为前进方向的依据,也就是说遇到数字“1”,则向“1”所对应的射线方向前进1个单位的距离,依次类推。请画出该点顺着圆周率小数点后N位依次前行的路线图。
clear all
clc
N=input('请输入N的值(建议10万以内), N= ');
x=[];
y=[];
x(1)=0;
y(1)=0;
j=1;
deta=2*pi/10;
c=char(vpa(sym('pi'),N+5));
for i=3:N
j=j+1;
if isequal(c(i),'0')
x(j)=x(j-1)+cos(deta*0);
y(j)=y(j-1)+sin(deta*0);
elseif isequal(c(i),'1')
x(j)=x(j-1)+cos(deta*1);
y(j)=y(j-1)+sin(deta*1);
elseif isequal(c(i),'2')
x(j)=x(j-1)+cos(deta*2);
y(j)=y(j-1)+sin(deta*2);
elseif isequal(c(i),'3')
x(j)=x(j-1)+cos(deta*3);
y(j)=y(j-1)+sin(deta*3);
elseif isequal(c(i),'4')
x(j)=x(j-1)+cos(deta*4);
y(j)=y(j-1)+sin(deta*4);
elseif isequal(c(i),'5')
x(j)=x(j-1)+cos(deta*5);
y(j)=y(j-1)+sin(deta*5);
elseif isequal(c(i),'6')
x(j)=x(j-1)+cos(deta*6);
y(j)=y(j-1)+sin(deta*6);
elseif isequal(c(i),'7')
x(j)=x(j-1)+cos(deta*7);
y(j)=y(j-1)+sin(deta*7);
elseif isequal(c(i),'8')
x(j)=x(j-1)+cos(deta*8);
y(j)=y(j-1)+sin(deta*8);
elseif isequal(c(i),'9')
x(j)=x(j-1)+cos(deta*9);
y(j)=y(j-1)+sin(deta*9);
end
if rem(j,500)==0
j
end
end
plot(x,y)
=====================================================
% 寻找比值最接近pi的两个素数
pri=primes(1000000);
n=length(pri)
loss=100;
for ii=1:n
x1=ceil(pri(ii)/4);
x2=ceil(pri(ii)/3);
pri_x1=primes(x1);
pri_x2=primes(x2);
m=length(pri_x2)-length(pri_x1);
if m>=1
for jj=1:m
mypi=pri(ii)/pri(length(pri_x1)+jj);
if loss>abs(mypi-pi)
loss=abs(mypi-pi);
pri(ii);
pri(length(pri_x1)+jj);
fprintf('loss is :%.20f , prime1 is : %d , prime2 is : %d \n', loss , pri(ii) ,pri(length(pri_x1)+jj) );
%转义序列 %.20f代表小数点后有20位小数。
fprintf('\n')
end
end
end
end
======================================================
生成随机彩色网格图。
1)repmat 复制矩阵
B = repmat(A,m,n)
B = repmat(A,[m n])
B = repmat(A,[m n p...])
这是一个处理大矩阵且内容有重复时使用,其功能是以A的内容堆叠在(MxN)的矩阵B中,B矩阵的大小由MxN及A矩阵的内容决定,如果A是一个3x4x5的矩阵,有B = repmat(A,2,3)则最后的矩阵是6x12x5
2)imshow函数
通过下面代码,理解图像的存储格式,以及显示方式imshow
%直接生产100,100,3的矩阵。
clear all
rgb=rand(100,100,3);
imshow(rgb)
%灰度图与彩色图的关系。
clear all
rgb1=rand(100,100,3)
rgb2=zeros(100,100,3)
rgb3=ones(100,100,3)
rgb4=ones(100,100,3)*0.5
imshow(rgb1)
imshow(rgb2)
imshow(rgb3)
imshow(rgb4)
%也可以采用先单独生成3个通道的颜色,
%再合并3个二维矩阵为一个三维的rgb矩阵,再显示。
clear all
k=100; % k行k列的彩图
r1=rand(k,k);
g1=rand(k,k);
b1=rand(k,k);
rgb=cat(3,r1,g1,b1);
imshow(rgb)
%完整程序:
clear all
k=5; %设置网格为k*k
n=100; %设置膨胀倍数n
rgb1=rand(k,k,3); %rgb1的初始化
rgb2=zeros(k*n,k*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k
for jj=1:k
rgb2((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = repmat(rgb1(ii , jj , : ) ,n ,n );
end
end
imshow(rgb2)
% 不用for循环,直接用REAPMAT赋值
clear all
k=3; %设置网格为k*k
n=200; %设置膨胀倍数n
r1=rand(k,k);
g1=rand(k,k);
b1=rand(k,k);
rgb1=cat( 3 , r1 , g1 , b1 ); %原始的k*k像素的小彩图
imshow(rgb1)
%下面开始膨胀操作。
rgb2=zeros( k*n , k*n , 3 ); %初始化rgb三维数组,初始值都设为0
rgb(1:100,1:100,:)=repmat(rgb1(1,1,:),100,100) ;
rgb(1:100,101:200,:)=repmat(rgb1(1,2,:),100,100) ;
rgb(1:100,201:300,:)=repmat(rgb1(1,3,:),100,100);
rgb(101:200,1:100,:)=repmat(rgb1(2,1,:),100,100);
rgb(101:200,101:200,:)=repmat(rgb1(2,2,:),100,100);
rgb(101:200,201:300,:)=repmat(rgb1(2,3,:),100,100);
rgb(201:300,1:100,:)=repmat(rgb1(3,1,:),100,100);
rgb(201:300,101:200,:)=repmat(rgb1(3,2,:),100,100);
rgb(201:300,201:300,:)=repmat(rgb1(3,3,:),100,100);
imshow(rgb)
================================
%以下为生成十字架的方法
clear all
k=10; %设置网格为k*k
n=50; %设置膨胀倍数n
rgb1=rand(k,k,3); %rgb1的初始化
rgb2=zeros(k*n,k*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k
for jj=1:k
rgb2((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = repmat(rgb1(ii , jj , : ) ,n ,n );
end
end
rgb2(1:200,1:200,:)=0.8;
rgb2(301:500,1:200,:)=0.8;
rgb2(1:200,301:500,:)=0.8;
rgb2(301:500,301:500,:)=0.8;
imshow(rgb2)
=================================
%以下为生成圆形的方法
clear all
k=6; %设置网格为k*k
n=120; %设置膨胀倍数n
rgb1=rand(k,k,3); %rgb1的初始化
rgb2=zeros(k*n,k*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k
for jj=1:k
rgb2((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = repmat(rgb1(ii , jj , : ) ,n ,n );
end
end
for x=1:k*n
for y=1:k*n
if (x-k*n/2).^2+(y-k*n/2).^2>(k*n/2)^2
rgb2(x,y,:)=0.8;
end
end
end
imshow(rgb2)
===============================
%以下为函数随机彩图的函数化方法
function [rgb2]=randcolor(inputArg1,inputArg2)
%本函数可以生成随机色彩网格图
k=inputArg1; %设置网格为k*k
n=inputArg2; %设置膨胀倍数n
rgb1=rand(k,k,3); %rgb1的初始化
rgb2=zeros(k*n,k*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k
for jj=1:k
rgb2((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = repmat(rgb1(ii , jj , : ) ,n ,n );
end
end
figure
imshow(rgb2)
end
===========================================================
%% 任务2:通过循环、pause()函数等技巧,来让如上的随机彩图每隔2秒钟刷新一次,刷新得最终次数自己来确定。
clear all
for t=1:10
k=5; %设置网格为k*k
n=150; %设置膨胀倍数n
rgb1=rand(k,k,3); %rgb1的初始化
rgb2=zeros(k*n,k*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k
for jj=1:k
rgb2((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = repmat(rgb1(ii , jj , : ) ,n ,n );
end
end
imshow(rgb2);
hold on
pause(3)
end
==================================
求圆周率Pi中前100万位里,是否出现你的生日(六位生日,如1999年3月1日,则认为生日为 990301),如果出现则具体出现了多少次,分别出现是小数点后的多少位?
clear all
p=char(vpa(pi,1000000));
n=length(p);
count=0;
for i=3:n-5
if p(i:i+5)==char('491001')
count=count+1;
i
end
end
count
%代码如下:
clear
t=1/2;
x1=sqrt(t);
y1=sqrt(t+t*x1);
for ii=1:20
x1=x1*y1;
y1=sqrt(t+t*y1);
end
p1=2/x1; %p1为我们用公式计算的圆周率
vpa(p1) %vpa显示p1的精确值
vpa(pi,50) %作为对比,用vpa显示真实的π的前50位
以下两个公式,难度较大:
x=1;
for k=10000:-1:2
x=1+(k-1)*k/x;
end
p1=2*(1+1/x)
x=1;
for k=103:-2:1
x=(2*(k-1)+1)^2/(2+x);
end
p1=4/(x+1)
作业4:制作一个中值滤波函数:zzlb() , 用于滤除图像的椒盐噪声
function p_new = zzlb(p_noise)
% 本函数可以对充满椒盐噪声的图像进行滤波,返回滤除椒盐噪声后的干净图像
%函数pic_new=zzlb(p_noise)中,输入参数p_noise为含有椒盐噪声的原始图像(uint8格式)
%函数返回值pic_new则为消除了椒盐噪声后的干净图像
%版权:gdcp_ccl_2021_05_25
p_new =p_noise;
[row,col,d]=size(p_noise); %测量输入图像的尺寸
if d==1
p=[ p_noise(1,1) , p_noise(1,:) , p_noise(1,col);
p_noise(:,1) , p_noise , p_noise(:,col);
p_noise(row,1), p_noise(row,:) , p_noise(row,col)];
%对原始图像边界填充生成胖一圈的图像p,在p上进行历遍操作
for n=2:row+1 %在新图p的2到row+1行,2到col+1列的区域历遍(即原图范围)
for m=2:col+1
tem=p(n-1:n+1,m-1:m+1); %以当前点为中心,构建一个3*3的临时矩阵
md=median(tem(:)); %找出这个矩阵所有元素的中位数
if p(n,m)==255|p(n,m)==0 %如果当前点为极端值(0或255)
p_new(n-1,m-1)=md; %则用刚才找到的中位数代替该极端值
end
end
end
end
if d==3 %如果是rgb彩图,则拆解成三个通道,对每个通道分别进行中值滤波
p_new(:,:,1) = zzlb(p_noise(:,:,1)); %红通道递归调用zzlv函数,进行降噪
p_new(:,:,2) = zzlb(p_noise(:,:,2)); %绿通道递归调用zzlv函数,进行降噪
p_new(:,:,3) = zzlb(p_noise(:,:,3)); %蓝通道递归调用zzlv函数,进行降噪
end
end
%调用上述函数
clear
p_orig =imread('D:\matlab2021\pic\yujinxiang_rgb.jpg');
p_noise=imread('D:\matlab2021\pic\yujinxiang_rgb_saltpepper.png');
p_new = zzlb(p_noise);
subplot(2,2,1),imshow(p_orig);
subplot(2,2,2),imshow(p_noise);
subplot(2,2,3),imshow(p_new);
PCA算法学习(Matlab实现)
PCA(主成分分析)算法,主要用于数据降维,保留了数据集中对方差贡献最大的若干个特征来达到简化数据集的目的。
实现数据降维的步骤:
1、将原始数据中的每一个样本用向量表示,把所有样本组合起来构成一个矩阵,通常需对样本矩阵进行处理,得到中性化样本矩阵
2、求样本矩阵的协方差矩阵
3、求协方差矩阵的特征值和特征向量
4、将求出的特征向量按照特征值的大小进行组合形成一个映射矩阵。并根据指定的PCA保留的特征个数取出映射矩阵的前n行或者前n列作为最终的映射矩阵。
5、用映射矩阵对数据进行映射,达到数据降维的目的。
中心化样本矩阵:先让样本矩阵中心化,即每一维度减去该维度的均值,然后直接用新的到的样本矩阵乘上它的转置,然后除以(N-1)即可,如下:
C = (X’*X)/(size(X,1)-1)%新得到的矩阵X乘上的它的转置
PCA算法Matlab实现:
1 function [newX,T,meanValue] = pca_row(X,CRate) 2 %每行是一个样本 3 %newX 降维后的新矩阵 4 %T 变换矩阵 5 %meanValue X每列均值构成的矩阵,用于将降维后的矩阵newX恢复成X 6 %CRate 贡献率 7 %计算中心化样本矩阵 8 meanValue=ones(size(X,1),1)*mean(X); 9 X=X-meanValue;%每个维度减去该维度的均值 10 C=X'*X/(size(X,1)-1);%计算协方差矩阵 11 12 %计算特征向量,特征值 13 [V,D]=eig(C); 14 %将特征向量按降序排序 15 [dummy,order]=sort(diag(-D)); 16 V=V(:,order);%将特征向量按照特征值大小进行降序排列 17 d=diag(D);%将特征值取出,构成一个列向量 18 newd=d(order);%将特征值构成的列向量按降序排列 19 20 %取前n个特征向量,构成变换矩阵 21 sumd=sum(newd);%特征值之和 22 for j=1:length(newd) 23 i=sum(newd(1:j,1))/sumd;%计算贡献率,贡献率=前n个特征值之和/总特征值之和 24 if i>CRate%当贡献率大于95%时循环结束,并记下取多少个特征值 25 cols=j; 26 break; 27 end 28 end 29 T=V(:,1:cols);%取前cols个特征向量,构成变换矩阵T 30 newX=X*T;%用变换矩阵T对X进行降维 31 end
1小时Matlab速成代码资料
这里是西电通院科协glanny的1小时matlab!将时长约48小时的内容压缩到1小时!适用于Matlab入门,考前抱佛脚以及数模赛前准备。删除了大量使用较少的函数,删除与基本编程语言重复的部分。全程干货,推荐有一定的编程基础之后观看,至少知道什么是变量、函数、循环和判断语句,最好也要会线性代数相关知识,知道矩阵运算。 代码及教案准备时长:107小时; 录制与编辑耗时:28小时; 最终视频总长度:59分37秒。
视频地址:
https://www.bilibili.com/video/BV1hE411Q7T4?from=search&seid=10107368026120817263
代码:
第1部分:变量定义和基本运算
%%
% 建议有C语言或其他编程基础,了解线性代数和矩阵相关知识
% https://ww2.mathworks.cn/help/matlab/
% 加*为了解内容
% 生成矩阵
% 直接法
a = [1,2,3;4,5,6;7,8,9];
% 冒号一维矩阵 a = 开始:步长:结束,步长为1可省略
b = 1:1:10; % 1,2,...10
b = 1:10; %与上一个等价
% 函数生成
% linspace(开始,结束,元素个数),等差生成指定元素数的一维矩阵,省略个数则生成100个
c = linspace(0,10,5);
% 特殊矩阵
e = eye(4); % eye(维数)单位阵
z = zeros(1,4); % zeros(维数)全零阵
o = ones(4,1); % ones(维数)全1阵
r = rand(4); % rand(维数)0~1分布随机阵
rn = randn(4); % randn(维数)0均值Gaussian分布随机阵
%%
% 矩阵运算
diag_a = diag(a,1); % diag(行向量,主对角线上方第k条斜线)用行向量生成对角阵
tril_a = tril(a,1); % tril(矩阵,主对角线上方第k条斜线)生成矩阵的下三角阵,triu上三角阵
% 加、减、乘、乘方
a*a
% 点运算
% a.*b , a./b , a.\b , a.^b 对应元素的*,/,\,^运算
a.*a
% 逆矩阵
pinv(a) % 伪逆矩阵,当a不是方阵,求广义逆矩阵;当a是可逆方阵,结果与逆矩阵相同
% 特征值,特征向量
[v,D] = eig(a); % 输出v为特征向量,D为特征值对角阵
% *行列式
det(a)
% *秩
rank(a)
% *伴随
compan(b)
%%
% 矩阵的修改
%部分替换
chg_a = a;
chg_a(2,3) = 4; % (行,列)元素替换
chg_a(1,:) = [2,2,2]; % (行,:)替换行,为[]删除该行
chg_a(:,1) = []; % (:,列)替换列,为[]删除该列
% 转置
T_a = a';
% 指定维数拼接
c1_a = cat(1,a,a); % 垂直拼接
c2_a = cat(2,a,a); % 水平拼接
% *变维
rs_a = reshape(a,1,9); % 元素个数不变,矩阵变为m*n
%%
% 信息获取
% 矩阵的行列数
[row_a, col_a] = size(a); % [行数,列数]
% 行列中最大的
len_a = length(a);
%%
% 多维数组
% 创建
% 直接法
mul_1(:,:,1) = [1,2,3;2,3,4];
mul_1(:,:,2) = [3,4,5;4,5,6];
% *扩展法
mul_2 = [1,2,3;2,3,4];
mul_2(:,:,2) = [3,4,5;4,5,6]; % 若不赋值第一页,第一页全为0
% cat法
mul_31 = [1,2,3;2,3,4];
mul_32 = [3,4,5;4,5,6];
mul_3 = cat(3,mul_31,mul_32); % 把a1a2按照“3”维连接
%%
% *字符串
% 创建
str0 = 'hello world'; % 单引号引起
str1 = 'I''m a student'; % 字符串中单引号写两遍
str3 = ['I''m' 'a' 'student']; % 方括号链接多字符串
str4 = strcat(str0, str1); % strcat连接字符串函数
str5 = strvcat(str0, str1); % strvcat连接产生多行字符串
str6 = double(str0); % 取str0的ASCII值,也可用abs函数
str7 = char(str6); % 把ASCII转为字符串
% 操作
% 比较
strcmp(str0, str1); % 相等为1,不等为0
strncmp(str0, str1, 3); % 比较前3个是否相等(n)
strcmpi(str0, str1); % 忽略大小写比较(i)
strncmpi(str0, str1, 3); % 忽略大小写比较前3个是否相等
% 查找替换
strfind(str0, str1); % 在str0找到str1的位置
strmatch(str1, str0); % 在str0字符串数组中找到str1开头的行数
strtok(str0); % 截取str0第一个分隔符(空格,tab,回车)前的部分
strrep(str0, str1, str2); % 在str0中用str2替换str1
% 其他
upper(str0); % 转大写,lower转小写
strjust(str0, 'right'); % 将str0右对齐,left左对齐,center中间对齐
strtrim(str0); % 删除str0开头结尾空格
eval(str0); % 将str0作为代码执行
%%
%转换
% ___2___ --> 如num2str,将数字转字符串; dec2hex,将十进制转十六进制
str_b = num2str(b);
% abs,double取ASCII码;char把ASCII转字符串
abs_str = abs('aAaA');
第2部分:程序结构
%%
a = 5;
x = [1, 2]; y =[3, 4];
%%
%选择结构
%if-elseif-else-end
if a>0
disp(x);
elseif a==0
disp(a);
else
disp(a-1);
end
%switch-case-otherwise-end
switch a
case 0
disp(a);
case 1
disp(a+1);
otherwise
disp('aaa');
end
%try-catch
try
z = x*y;
catch
z = x.*y; % 若try出错,则执行
end
disp(z);
%%
% 循环结构
% for 循环变量=初值:步长:终值 - end
for i=0:1:10 % 步长为负,则初值大于终值
disp(i); % 循环体内不可对循环变量做修改
end
% while-end
while a>2
disp(a);
a = a-1;
end
%%
%程序控制
%continue 跳过当次循环剩下语句,进入下一循环
%break 跳出当前循环
%return 跳出程序并返回
%%
%m文件
%脚本文件:没有输入输出参数,执行后变量结果返回工作空间,可直接运行
%以下是脚本文件,文件名假设为exp.m
%**********************************************
clear
r = 5;
s = pi*r*r;
p = 2*pi*r;
disp(s)
disp(p)
%**********************************************
%以下是调用
%**********************************************
exp
%**********************************************
%函数文件:以function开头,有输入输出,变量为局部变量不返回工作空间,需要调用
%以下是函数文件
%**********************************************
function [s, p] = circ(r) % 文件命名应与函数名一致,系统找文件名circ.m
%CIRC 计算圆面积和周长 % 简单说明
%参数:输入参数r:圆半径;输出参数s:圆面积,p:周长 % 详细说明
s = pi*r*r;
p = 2*pi*r;
end
%**********************************************
%以下是调用
%**********************************************
[a, b] = circ(5); % 返回为多个参数时,若写a = circ(5)则保留第一个返回值
%**********************************************
%*以下是带子函数的函数文件
%**********************************************
function y = key(w) % 主函数放第一个,函数名为key
if w==0
y = type0(w); % 调用子函数type0
else
y = type1(w);
end
end
function y0 = type0(a) % 子函数,各子函数之间顺序无所谓
y0 = a+1;
end
function y1 = type1(a)
y1 = a+4;
end
%**********************************************
%*函数输入输出参数可以不定
%nargin:输入参数个数,nargout:输出参数个数
%varargin:输入参数内容的元胞数组,varargout:输出参数
%以下是函数文件
%**********************************************
function varargout = idk(varargin)
x = length(varargin);
varargout{1} = x;
varargout{2} = x+1;
end
%**********************************************
第3部分:图像绘制
%%
x = 0:0.1:2*pi;
y1 = sin(x);
y2 = cos(x);
%%
% 二维曲线绘制
% 基本函数
% plot(y)
% y为向量
plot(y1); % 纵坐标为y的值;横坐标自动为元素序号(角标+1),此处为1~9
% y为矩阵
figure; % 开启新绘图窗口,下一次绘图在新窗口
y = [y1', y2'];
plot(y); % 当y为矩阵,按每一列画出曲线,颜色自动区分
% plot(x, y)
% xy为向量
plot(x, y1); % 先绘制曲线
% plot(x1, y1, x2, y2...)
plot(x, y1, x, y2); % 在同一个窗口同一坐标轴绘制多条曲线
% 线性图形格式设置
% 线形颜色数据点
plot(x, y1, 'b:o'); % 蓝色 点线 圆圈
% b蓝 g绿 r红 c青 m紫 y黄 k黑 w白
% -实线 :点线 --虚线 -.点画线
% .实点 o圆圈 x叉 +十字 *星号 s方块 d钻石 v下三角 ^上三角 <左三角 >右三角 p五角星 h六角星
% 坐标轴
plot(x, y1);
axis([-1*pi, 3*pi, -1.5, 1.5]); % 规定横纵坐标范围
% 图形修饰
% 标题标签
title('a title'); % 图像标题
xlabel('this is x'); % x轴标记,同理还有ylabel,zlabel
%图例设置
legend('hahaha', 'location', 'best'); % str的顺序与绘图顺序一致; 'best'指图例位置最佳化,还有其他位置
%图形保持
plot(x, y1);
hold on; % 在原有窗口y1曲线上增加绘制下一个图形
plot(x, y2); % y2在同一窗口内被绘制
hold off;
%分割绘制
subplot(2, 2, 1); % 分割成2x2区域,在第一块区域绘制下一个图形
plot(x, y1); % y1被绘制在4块区域的第一块
subplot(2, 2, 2); % 分割方法相同,区域改变
plot(x, y2); % y2在第二块区域
%%
%*二维特殊图形绘制
%柱状图
bar(x, y, width, '参数'); % x横坐标向量,m个元素; y为向量时,每个x画一竖条共m条,矩阵mxn时,每个x画n条;
% width宽度默认0.8,超过1各条会重叠;
% 参数有grouped分组式,stacked堆栈式; 默认grouped
% bar垂直柱状图,barh水平柱状图,bar3三维柱状图,barh3水平三维柱状图(三维多一个参数detached, 且为默认)
%饼形图
pie(x, explode, 'lable'); % x为向量显示每个元素占总和百分比, 为矩阵显示每个元素占所有总和百分比
% explode向量与x同长度,为1表示该元素被分离突出显示,默认全0不分离
% pie3绘制三维饼图
%直方图
hist(y, n); % y为向量,把横坐标分为n段绘制
hist(y, x); % x为向量,用于指定每段中间值, 若取N = hist(y, x), N为每段元素个数
%离散数据图
stairs(x, y, 'b-o'); % 阶梯图,参数同plot
stem(x, y, 'fill'); % 火柴杆图,参数fill是填充火柴杆,或定义线形
candle(HI, LO, CL, OP); % 蜡烛图:HI为最高价格向量,LO为最低价格向量,CL为收盘价格向量,OP为开盘价格向量
%向量图
compass(u, v, 'b-o'); % 罗盘图横坐标u纵坐标v
compass(Z, 'b-o'); % 罗盘图复向量Z
feather(u, v, 'b-o'); % 羽毛图横坐标u纵坐标v
feather(Z, 'b-o'); % 羽毛图复向量Z
quiver(x, y, u, v); % 以(x, y)为起点(u, v)为终点向量场图
%极坐标图
% polar(theta, rho, 'b-o'); % 极角theta, 半径rho
theta = -pi:0.01:pi;
rho = sin(theta);
polar(theta, rho, 'b')
%对数坐标图
semilogx(x1, y1, 'b-o'); % 把x轴对数刻度表示, semilogy是y轴对数刻度表示,loglog是两个坐标都用对数表示
%双纵坐标
plotyy(x1, y1, x2, y2, 'fun1', 'fun2'); % fun规定了两条条线的绘制方式,如plot,semilogx,semilogy,loglog,stem等
%函数绘图
f = 'sin(2*x)';
ezplot(f, [0, 2*pi]); % 绘制f并规定横坐标范围,也有[xmin, xmax, ymin, ymax]
x = '2*cos(t)';
y = '4*sin(t)';
ezplot(x, y); % 绘制x(t),y(t)在[0, 2*pi]图像, 也可以在最后用[tmin, tmax]规定t的范围
%%
%三维曲线曲面绘制
%三维曲线
x = 0:0.1:2*pi;
y = sin(x); z = cos(x);
plot3(x, y, z, 'b-*');
%三维曲面
%三维网格
x = -5:0.1:5; % 规定了x轴采样点,也规定了x轴范围
y = -4:0.1:4; % 规定了y轴采样点,也规定了y轴范围
[X, Y] = meshgrid(x, y); % 得到了xoy面网格点
Z = X.^2+Y.^2;
mesh(X, Y, Z) % XY是meshgrid得到的网格点,Z是网格顶点,c是用色矩阵可省略
%三维表面图
x = -5:0.1:5;
y = -4:0.1:4;
[X, Y] = meshgrid(x, y);
Z = X.^2+Y.^2; % 以上部分同上
surf(X, Y, Z) % 与上一个类似
第4部分:多项式
%%
%多项式
%创建
p = [1, 2, 3, 4]; % 系数向量,按x降幂排列,最右边是常数
f1 = poly2str(p, 'x'); % 生成好看的字符串 f1 = x^3 + 2 x^2 + 3 x + 4,不被认可的运算式
f2 = poly2sym(p); % 生成可用的符号函数 f2 = x^3 + 2*x^2 + 3*x + 4
%求值
x = 4;
y1 = polyval(p, x); % 代入求值;若x1为矩阵,则对每个值单独求值
%求根
r = roots(p); % p同上,由系数求根,结果为根植矩阵
p0 = poly(r); % 由根求系数,结果为系数矩阵
%%
%数据插值
%一维插值
%yi = interp1(X, Y, xi, 'method')
X = [-3, -1, 0, 1, 3];
Y = [9, 1, 0, 1, 9]; % XY为已知点横纵坐标向量
y2 = interp1(X, Y, 2); % 差值预估在x=2的y的值,x不能超过已知范围(此处x<3)
y2m = interp1(X, Y, 2, 'spline'); % 用spline方法(三次样条)差值预估在x=2的y的值
%二维插值
%zi = interp1(X, Y, Z, xi, yi, 'method')
%%
X = [2, 3, 9, 15, 6, 7, 4];
A = [1, 7, 2; 9, 5, 3; 8, 4 ,6];
B = [1, 7, 3; 9, 5, 3; 8, 4 ,6];
%数据统计
%矩阵最大最小值
y = max(X); % 求矩阵X的最大值,min最小值
[y, k] = max(X); % 求最大值,k为该值的角标
[y, k] = max(A, [], 2); % A是矩阵,'2'时返回y每一行最大元素构成的列向量,k元素所在列;'1'时与上述相同
%均值和中值
y = mean(X); % 均值
y = median(X); % 中值
y = mean(A, 2); % '2'时返回y每一行均值构成的列向量;'1'时与上述相同
y = median(A, 2); % '2'时返回y每一行中值构成的列向量;'1'时与上述相同
%排序
Y = sort(A, 1, 'ascend'); % sort(矩阵, dim, 'method')dim为1按列排序,2按行排序;ascend升序,descend降序
[Y, I] = sort(A, 1, 'ascend'); % I保留了元素之前在A的位置
%求和求积累加累乘
y = sum(X); % 求和
y = prod(X); % 求积
y = cumsum(X); % 累加
y = cumprod(X); % 累乘
%%
%*数值计算
%最(极)值
%多元函数在给定初值附近找最小值点
x = fminsearch(fun, x0);
%函数零点
x = fzero(fun, x0); % 在给定初值x0附近找零点
第5部分:符号函数
%%
%符号对象创建
%sym函数
p = sin(pi/3);
P = sym(p, 'r'); % 用数值p创建符号常量P;'d'浮点数'f'有理分式的浮点数'e'有理数和误差'r'有理数
%syms函数
syms x; % 声明符号变量
f = 7*x^2 + 2*x+9; % 创建符号函数
%符号运算
% 加减乘除外
% '转置 ; ==相等 ; ~=不等
% sin, cos, tan; asin, acos, atan 三角反三角
% sinh, cosh, tanh; asinh, acosh, atanh 双曲反双曲
% conj复数共轭;real复数实部;imag复数虚部;abs复数模;angle复数幅角
% diag矩阵对角;triu矩阵上三角;tril矩阵下三角;inv逆矩阵;det行列式;rank秩;poly特征多项式;
% |----expm矩阵指数函数;eig矩阵特征值和特征向量;svd奇异值分解;
%符号对象精度转换
digits; % 显示当前用于计算的精度
digits(16); % 将计算精度改为16位,降低精度有时可以加快程序运算速度或减少空间占用
a16 = vpa(sqrt(2)); % vpa括起的运算使sqrt(2)运算按照规定的精度执行
a8 = vpa(sqrt(2), 8); % 在vpa内控制精度,离开这一步精度恢复
%%
%符号多项式函数运算
%*符号表达形式与相互转化
%多项式展开整理
g = expand(f); % 展开
h = collect(g); % 整理(默认按x整理)
h1 = collect(f, x); % 按x整理(降幂排列)
%因式分解展开质因数
fac = factor(h); % 因式分解
factor(12); % 对12分解质因数
%符号多项式向量形式与计算
syms a b c;
n = [a, b, c];
roots(n); % 求符号多项式ax^2+bx+c的根
n = [1, 2, 3];
roots(n); % 求符号多项式带入a=1, b=2, c=3的根
%*反函数
fi = finverse(f, x); % 对f中的变量x求反函数
%%
%符号微积分
%函数的极限和级数运算
% 常量a,b
%极限
limit(f, x, 4); % 求f(x), x->4
limit(f, 4); % 默认变量->4
limit(f); % 默认变量->0
limit(f, x, 4, 'right'); % 求f(x), x->4+, 'left' x->4-
%*基本级数运算
%求和
symsum(s, x, 3, 5); % 计算表达式s变量x从3到5的级数和,或symsum(s, x, [a b])或symsum(s, x, [a;b])
symsum(s, 3, 5); % 计算s默认变量从3到5的级数和
symsum(s); % 计算s默认变量从0到n-1的级数和
%一维泰勒展开
taylor(f, x, 4); % f在x=4处展开为五阶泰勒级数
taylor(f, x); % f在x=0处展开为五阶泰勒级数
taylor(f); % f在默认变量=0处展开为五阶泰勒级数
%符号微分
%单变量求导(单变量偏导)
n = 1; % 常量n
fn = diff(f, x, n); % f对x的n阶导
f1 = diff(f, x); % f对x的1阶导
diff(f, n); % f对默认变量的n阶导
diff(f); % 默认变量1阶导
%多元偏导
fxy = diff(f, x, y); % 先求x偏导,再求y偏导
fxyz = diff(f, x, y, z); % 先求x偏导,再求y偏导,再求z偏导
%符号积分
%积分命令
int(f, x, 1, 2); % 函数f变量x在1~2区间定积分
int(f, 1, 2); % 函数f默认变量在ab区间定积分
int(f, x); % 函数f变量x不定积分
int(f); % 函数f默认变量不定积分
% 傅里叶,拉普拉斯,Z变换
%%
%*符号方程求解
%符号代数方程
%一元方程
eqn1 = a*x==b;
S = solve(eqn1); % 返回eqn符号解
%多元方程组
eqn21 = x-y==a;
eqn22 = 2*x+y==b;
[Sx, Sy] = solve(eqn21, eqn22, x, y); % [Svar1,...SvarN]=solve(eqn1,...eqnM, var1,...varN),MN不一定相等
[Sxn, Syn] = solve(eqn21, eqn22, x, y, 'ReturnCondition', true); % 加上参数ReturnCondition可返回通解及解的条件
% 其他参数(参数加上true生效)
% IgnoreProperty,忽略变量定义时一些假设
% IgnoreAnalyticConstraints,忽略分析限制;
% MaxDegree,大于3解显性解;
% PrincipleValue,仅主值
% Real,仅实数解
%非线性fsolve
X = fsolve(fun, X0, optimset(option)); % fun函数.m文件名;X0求根初值;option选项如('Display','off')不显示中间结果等
知乎上的计算机领域大神。
作者:熊风
链接:https://www.zhihu.com/question/31168392/answer/50977180
花一些时间盘点一下这些知乎上的大神,仅涉及计算机领域。(如果信息有错误,请大家指正。我也一直是仰望这些大神,只是在江湖上听说过他们的传说,细节也不了解)
2016.11.14 更新,每过一段时间就会发现知乎又冒出了很多计算机领域大神。我这个答案列的并不全;知乎真是藏龙卧虎之地,很多同样满足条件的人我可能遗漏了。
1. 算法竞赛领域 入选标准:拿过IOI或者ACM总决赛金牌,处于全球前几名的水平。 (1)
陈立杰,高一被清华录取,13年国际信息学奥林匹克竞赛(IOI)世界冠军,现在清华大学姚班就读。2016年获得清华特奖,以下是他评选特奖的简历:“ 男,交叉信息研究院计科30班。专业课学分绩98.3,信息学国际奥林匹克竞赛全球第1名。以第一作者身份在AAMAS、COLT和ISAAC上发表论文,并另有5篇论文在投。访问MIT期间,解决了著名量子信息学者John Watrous在2002年提出的open problem并准备投往计算机理论顶级会议STOC。长期参与中国信息学竞赛的组织和命题工作。” (2)
与上面那个是好基友。15岁因为信息学竞赛被清华签约,VK Cup击败当世第一人tourist夺得冠军,12年IOI金牌(世界第三)。现在MIT就读 (3)
高一被清华录取,OI界大神,现在清华大学姚班就读 (4)
高一被清华录取,高三百度之星编程竞赛冠军,13年IOI第二名。2015年ACM总决赛金牌,现在清华大学姚班就读。 (5)
郭晓旭,江湖人称“叉姐”。代表上海交大参加过两次ACM总决赛,一次银牌,一次金牌(世界第二) (6)
巫泽俊,浙大传奇,2010年ACM总决赛世界冠军。 (7)
96年IOI金牌,保送清华。现在是搜狗CEO 2015.11.23更新: (8)陈启峰 07年IOI金牌。初中参加高中的信息学竞赛拿到了保送清华的名额;高中时发明了size balanced tree这种数据结构,被后来的信息学竞赛选手广为使用,拿到了IOI金牌;本科去了香港科技大学,在本科期间发过顶级会议论文,2012年本科毕业后去了斯坦福大学计算机系读PhD (9)唐文斌 06年IOI金牌。高中保送清华姚班,并且进入过TCO世界决赛;清华姚班本科,本科期间获得过Yao Award一等奖,ACM世界总决赛银牌(世界第六),挑战杯特等奖;清华硕士期间创立了Face++,先后担任过CTO, CEO 现在已经是业界知名人物了 (10)戴文渊 上海交大的神话人物,05年ACM世界冠军。硕士期间和杨强一起发了很多篇质量极高的论文(transfer learning),发顶级会议如同探囊取物。硕士毕业后去百度工作,三年不到升到T10(当年整个百度T10才几个人),期间拿过百度最高奖。而后去诺亚方舟实验室工作过一段时间,现在在创业。 2016.11.14 更新 (11)Ce Jin - 知乎 金策,世界数独锦标赛冠军,NOI 2014年全国冠军,2016年IOI世界冠军,现在清华大学姚班就读。 (12)Apia Du 杜瑜皓,15年IOI金牌(世界第四),16年facebook黑客杯世界第二。codeforces上目前rating最高的中国选手(仅次于传奇选手tourist和petr) . 现在清华大学姚班就读。 …… 我觉得这些人都是天才,智商高的令人发指。虽然很多都在读书阶段,但是相信以他们的智商,以后肯定在业界也是大神,很有可能成为顶级大牛。不管怎么样,他们都已经在算法竞赛的江湖上留下了传说。
2. 人工智能领域(ML,CV) 入选标准:足够的顶级会议/期刊论文。圈内的影响力和知名度在同龄人中处于顶级水平 (1)
上面有人提过了。清华本科,伯克利PhD, caffe作者,对深度学习领域有很大影响。之前是Google Research Scientist,现在在Facebook负责人工智能平台的底层开发。 (2)
上交本科,CMU PhD在读,百度少帅(百度少帅的选择标准:30岁以下,职级T9-T10, 全国只有几个人,薪酬100万RMB+) (3)
侯晓迪,上交本科,加州理工PhD,现任知图科技CTO。如
所说,华人年轻AI学者里单篇论文引用数最高的人,超过很多名校教授。注意一点,他发那篇高引用论文的时候才读大三,真是给跪了。 他在知乎上的两个匿名回答最让我印象深刻,简直把我吓哭,一看就感觉是非人类……如何能在本科三年级就发表论文? - 匿名用户的回答 前一晚没睡好,第二天如何保持旺盛精力? - 匿名用户的回答(4)
和
王乃岩,浙大本科,香港科技大学博士。Tusimple(北京图森互联科技有限责任公司)首席科学家,套用一下tusimple官网的介绍:“2014 Google PhD Fellow计划入选者(中国仅4人入选,全球共38位),多次在国际数据挖掘和计算机视觉比赛中名列前茅 (ImageNet 2014第三名,Kaggle Data Science Bowl第二名,KDD Cup 2013第六名),将深度学习应用于目标追踪领域全球第一人”。 石建萍,浙大本科,香港中文大学博士。本科期间第一作者发表CVPR oral, 13年微软奖学金获得者(亚洲10个),16年image net竞赛scene parsing项目世界冠军。 (5)田渊栋 上交本科,CMU PhD,在Facebook AI Research. 拿过ICCV马尔奖提名 (6)曹旭东 商汤科技执行研发总监。清华大学物理系,前微软研究员。 (7)姚邦鹏 清华本科,斯坦福PhD。计算机视觉大牛Li Feifei的学生,现在在华尔街工作。“有个故事,到Feifei的主页上查学生去向,在一群硅谷scientist,professor中间有一个空白的,这个人去了街上,收入是其他人的和” 。那个“去了街上”的学生就是姚邦鹏,出处见被称为业界大牛的斯坦福计算机视觉实验室的李飞飞具体牛在哪里? - 姚邦鹏的回答2016.11.14 更新 (8)SS Wang 王树森,浙江大学本科和博士,师从国内机器学习大牛张志华。百度奖学金和微软奖学金的获得者,和大牛张潼、Michael Jordan一起发过几篇JMLR。现在在伯克利做post (9)卢策吾 - 知乎 香港中文大学博士。青年千人计划入选者,现在是上海交大教授。 (10)周博磊 上交本科,港中文硕士,MIT PhD在读。2011年微软奖学金获得者,2016年Facebook Graduate Fellowship 获得者。 (11)林达华 - 知乎 中科大本科,港中文硕士,MIT PhD毕业。2010年NIPS最佳学生论文。 现在是香港中文大学教授。 (12)刘知远 - 知乎 刘知远,清华本科和博士,现在是清华大学计算机系自然语言处理实验室的助理教授
3. 信息安全领域 入选标准:顶级黑客,在安全圈有足够的声望
于旸,绿盟科技高级研究员。信息安全界的教主,国内顶级黑客。
吴翰清,国内顶级黑客。西安交大少年班毕业,大学期间创办民间组织幻影,阿里巴巴集团最年轻的高级安全专家,创新工场安全宝任联合副总裁,现在好像又回到阿里了(P10) 大家可以关注一下道哥的博客或者知乎专栏,个人感觉很有干货
阿里巴巴集团,资深安全专家(P9),国内顶级黑客。余弦和黑哥,国内顶级黑客,都在知道创宇,都是安全界大名鼎鼎的人物。
4. 其它 入选标准:同龄人中顶级水平
顾研,NOI金牌保送清华,清华本科,CMU PhD在读,发了很多牛逼论文。看好成为学术界大牛
NOI金牌保送清华, 开源社区名人。高中时就写出了Open CC,本科先后在MSRA,Hulu,Google,Facebook实习,毕业时横扫各大公司offer,包括阿里星。在阿里星面试的时候,阿里高层对他评价极高(有兴趣可以搜一下那张泄露的面试结果截图)王钦石 s-quark 王钦石,高二保送清华,黑龙江省历史上第一位NOI金牌。现在姚班就读Botao Amber Hu 胡伯涛,NOI保送清华。从高中就开始投资股市和房产,赚了不可想象的一笔大钱(出处见byvoid的博客这一年来 - BYVoid);大一拿到ACM区域赛冠军,转入清华姚班;本科期间先后在Google,MSRA,香港科技大学实习,发表了五篇顶会论文,毕业时同时拿到了Facebook、Google、Twitter和Standford的offer。毕业后去了stanford 现在已经回国创业
关于温兆伦,他们确实是技术大神,但他们应该还离最顶级水平有一段距离吧。我所理解的顶级,要么在某项大家都认可的竞赛中拿到世界顶级的名次;要么在业界有足够的代表作和声望积累,圈子内的人都知道你;要么直接背景碾压,一看background就感觉是非人类。 不过温兆伦的水平显然也是非常高的,再加上他们在知乎上很活跃,给大家分享了很多干货,对知乎的贡献应该比我上面列的用户都要大。
知乎上的计算机大神实在实在是太多了…… 写完这个答案,我觉得我应该滚回去写代码了。。。
更新:竟然一下子有这么多赞,忍不住取消匿名了。之前匿名的原因是感觉不小心黑了轮子哥一把,希望温赵轮三位大神不要见怪,你们也是我技术上的榜样(逃