只有五行的Floyd最短路算法
此算法由Robert W. Floyd(罗伯特·弗洛伊德)于1962年发表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍尔)也独立发表了这个算法。Robert W.Floyd这个牛人是朵奇葩,他原本在芝加哥大学读的文学,但是因为当时美国经济不太景气,找工作比较困难,无奈之下到西屋电气公司当了一名计算机操作员,在IBM650机房值夜班,并由此开始了他的计算机生涯。
暑假,小哼准备去一些城市旅游。有些城市之间有公路,有些城市之间则没有,如下图。为了节省经费以及方便计划旅程,小哼希望在出发之前知道任意两个城市之前的最短路程。
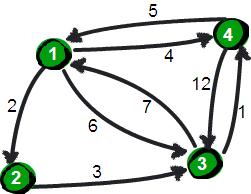
上图中有4个城市8条公路,公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。
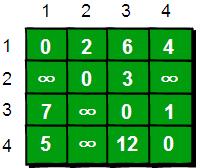
现在需要一个数据结构来存储图的信息,我们仍然可以用一个4*4的矩阵(二维数组e)来存储。比如1号城市到2号城市的路程为2,则设e[1][2]的值为2。2号城市无法到达4号城市,则设置e[2][4]的值为∞。另外此处约定一个城市自己是到自己的也是0,例如e[1][1]为0,具体如下。
现在回到问题:如何求任意两点之间最短路径呢?通过之前的学习我们知道通过深度或广度优先搜索可以求出两点之间的最短路径。所以进行n2遍深度或广度优先搜索,即对每两个点都进行一次深度或广度优先搜索,便可以求得任意两点之间的最短路径。可是还有没有别的方法呢?
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4号城市到3号城市(4->3)的路程e[4][3]原本是12。如果只通过1号城市中转(4->1->3),路程将缩短为11(e[4][1]+e[1][3]=5+6=11)。其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1][2]+e[2][3]=2+3=5)。所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。好,下面我们将这个问题一般化。
当任意两点之间不允许经过第三个点时,这些城市之间最短路程就是初始路程,如下。

如现在只允许经过1号顶点,求任意两点之间的最短路程,应该如何求呢?只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是从i号顶点到j号顶点之间的路程。e[i][1]+e[1][j]表示的是从i号顶点先到1号顶点,再从1号顶点到j号顶点的路程之和。其中i是1~n循环,j也是1~n循环,代码实现如下。
1 2 3 4 5 6 7 8 | for(i=1;i<=n;i++) { for(j=1;j<=n;j++) { if ( e[i][j] > e[i][1]+e[1][j] ) e[i][j] = e[i][1]+e[1][j]; } } |
在只允许经过1号顶点的情况下,任意两点之间的最短路程更新为:
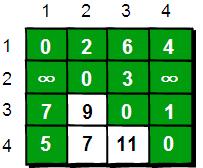
通过上图我们发现:在只通过1号顶点中转的情况下,3号顶点到2号顶点(e[3][2])、4号顶点到2号顶点(e[4][2])以及4号顶点到3号顶点(e[4][3])的路程都变短了。
接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。如何做呢?我们需要在只允许经过1号顶点时任意两点的最短路程的结果下,再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小,代码实现为如下。
1 2 3 4 5 6 7 8 | //经过1号顶点 for(i=1;i<=n;i++) for(j=1;j<=n;j++) if (e[i][j] > e[i][1]+e[1][j]) e[i][j]=e[i][1]+e[1][j]; //经过2号顶点 for(i=1;i<=n;i++) for(j=1;j<=n;j++) if (e[i][j] > e[i][2]+e[2][j]) e[i][j]=e[i][2]+e[2][j]; |
在只允许经过1和2号顶点的情况下,任意两点之间的最短路程更新为:
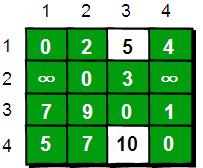
通过上图得知,在相比只允许通过1号顶点进行中转的情况下,这里允许通过1和2号顶点进行中转,使得e[1][3]和e[4][3]的路程变得更短了。
同理,继续在只允许经过1、2和3号顶点进行中转的情况下,求任意两点之间的最短路程。任意两点之间的最短路程更新为:
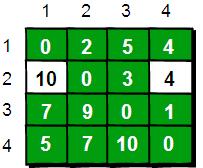
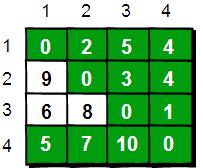
最后允许通过所有顶点作为中转,任意两点之间最终的最短路程为:
整个算法过程虽然说起来很麻烦,但是代码实现却非常简单,核心代码只有五行:
1 2 3 4 5 | for(k=1;k<=n;k++) for(i=1;i<=n;i++) for(j=1;j<=n;j++) if(e[i][j]>e[i][k]+e[k][j]) e[i][j]=e[i][k]+e[k][j]; |
这段代码的基本思想就是:最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转,求任意两点之间的最短路程。用一句话概括就是:从i号顶点到j号顶点只经过前k号点的最短路程。其实这是一种“动态规划”的思想,关于这个思想我们将在《啊哈!算法2——伟大思维闪耀时》在做详细的讨论。下面给出这个算法的完整代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | #include <stdio.h> int main() { int e[10][10],k,i,j,n,m,t1,t2,t3; int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值 //读入n和m,n表示顶点个数,m表示边的条数 scanf("%d %d",&n,&m); //初始化 for(i=1;i<=n;i++) for(j=1;j<=n;j++) if(i==j) e[i][j]=0; else e[i][j]=inf; //读入边 for(i=1;i<=m;i++) { scanf("%d %d %d",&t1,&t2,&t3); e[t1][t2]=t3; } //Floyd-Warshall算法核心语句 for(k=1;k<=n;k++) for(i=1;i<=n;i++) for(j=1;j<=n;j++) if(e[i][j]>e[i][k]+e[k][j] ) e[i][j]=e[i][k]+e[k][j]; //输出最终的结果 for(i=1;i<=n;i++) { for(j=1;j<=n;j++) { printf("%10d",e[i][j]); } printf("\n"); } return 0; } |
有一点需要注意的是:如何表示正无穷。我们通常将正无穷定义为99999999,因为这样即使两个正无穷相加,其和仍然不超过int类型的范围(C语言int类型可以存储的最大正整数是2147483647)。在实际应用中最好估计一下最短路径的上限,只需要设置比它大一点既可以。例如有100条边,每条边不超过100的话,只需将正无穷设置为10001即可。如果你认为正无穷和其它值相加得到一个大于正无穷的数是不被允许的话,我们只需在比较的时候加两个判断条件就可以了,请注意下面代码中带有下划线的语句。
A*寻路算法C++简单实现
参考文章:
http://www.policyalmanac.org/games/aStarTutorial.htm 这是英文原文《A*入门》,最经典的讲解,有demo演示
http://www.cnblogs.com/technology/archive/2011/05/26/2058842.html 这是国人翻译后整理的简版,有简单代码demo,不过有些错误,讲得很清晰,本文图片来自这篇
http://blog.csdn.net/b2b160/article/details/4057781 一片关于寻路算法的综述
A*寻路算法是游戏中常用的AI算法,这里用C++简单实现了一下算法,便于理解。
搜索区域
如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块。
开始寻路
1.从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.
2.寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.
3.从"开启列表"中删除起点 A, 并将起点 A 加入"关闭列表", "关闭列表"中存放的都是不需要再次检查的方格
图中浅绿色描边的方块表示已经加入 "开启列表" 等待检查. 淡蓝色描边的起点 A 表示已经放入 "关闭列表" , 它不需要再执行检查.
从 "开启列表" 中找出相对最适宜的方块, 通过公式 F=G+H 来计算.
F = G + H
G 表示从起点 A 移动到网格上指定方格的移动耗费 (可沿斜方向移动).
H 表示从指定的方格移动到终点 B 的预计耗费 (H 有很多计算方法, 本文代码使用简单的欧几里得距离计算方法).
我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算 FGH, 图中方块的左上角数字表示 F, 左下角表示 G, 右下角表示 H. 看看是否跟你心里想的结果一样?
从 "开启列表" 中选择 F 值最低的方格 C (绿色起始方块 A 右边的方块), 然后对它进行如下处理:
(如果C上方和下方都是障碍物的话会走入死胡同吗?不会,根据算法,这时候C会被直接放到关闭列表,没有发生任何节点的F更新和父节点更新)
4.把它从 "开启列表" 中删除, 并放到 "关闭列表" 中.
5.检查它所有相邻并且可以到达 (障碍物和 "关闭列表" 的方格都不考虑) 的方格. 如果这些方格还不在 "开启列表" 里的话, 将它们加入 "开启列表", 计算这些方格的 G, H 和 F 值各是多少, 并设置它们的 "父方格" 为 C.
6.如果某个相邻方格 D 已经在 "开启列表" 里了, 检查如果用新的路径 (就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的 "父方格" 改为目前选中的方格 C, 然后重新计算它的 F 值和 G 值 (H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的 G 值比较高, 就说明经过 C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.
如图, 我们选中了 C 因为它的 F 值最小, 我们把它从 "开启列表" 中删除, 并把它加入 "关闭列表". 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已经加入到 "关闭列表" 了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 C 下面的那个格子, 它目前的 G 是14, 如果通过 C 到达它的话, G将会是 10 + 10, 这比 14 要大, 因此我们什么也不做.
然后我们继续从 "开启列表" 中找出 F 值最小的, 但我们发现 C 上面的和下面的同时为 54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 C 下面的那个方块 D.
D 右边已经右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进 "开启列表" 呢? 因为如果 C 下面的那块也不可以走, 想要到达 C 右下角的方块就需要从 "方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)
就这样, 我们从 "开启列表" 找出 F 值最小的, 将它从 "开启列表" 中移掉, 添加到 "关闭列表". 再继续找出它周围可以到达的方块, 如此循环下去...
那么什么时候停止呢? —— 当我们发现 "开始列表" 里出现了目标终点方块的时候, 说明路径已经被找到.
输出路径
如上图所示, 除了起始方块, 每一个曾经或者现在还在 "开启列表" 里的方块, 它都有一个 "父方块", 通过 "父方块" 可以索引到最初的 "起始方块", 这就是路径.
算法伪码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | 把起始格添加到 "开启列表" do { 寻找开启列表中F值最低的格子, 我们称它为当前格. 把它切换到关闭列表. 对当前格相邻的8格中的每一个 if (它不可通过 || 已经在 "关闭列表" 中) { 什么也不做. } if (它不在开启列表中) { 把它添加进 "开启列表", 把当前格作为这一格的父节点, 计算这一格的 FGH if (它已经在开启列表中) { if (用G值为参考检查新的路径是否更好, 更低的G值意味着更好的路径) { 把这一格的父节点改成当前格, 并且重新计算这一格的 GF 值. } } while( 目标格已经在 "开启列表", 这时候路径被找到) 如果开启列表已经空了, 说明路径不存在. 最后从目标格开始, 沿着每一格的父节点移动直到回到起始格, 这就是路径. |
C++实现代码
Astar.h
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | #pragma once /*//A*算法对象类*/ #include <vector> #include <list> const int kCost1=10; //直移一格消耗 const int kCost2=14; //斜移一格消耗 struct Point { int x,y; //点坐标,这里为了方便按照C++的数组来计算,x代表横排,y代表竖列 int F,G,H; //F=G+H Point *parent; //parent的坐标,这里没有用指针,从而简化代码 Point(int _x,int _y):x(_x),y(_y),F(0),G(0),H(0),parent(NULL) //变量初始化 { } }; class Astar { public: void InitAstar(std::vector<std::vector<int>> &_maze); std::list<Point *> GetPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner); private: Point *findPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner); std::vector<Point *> getSurroundPoints(const Point *point,bool isIgnoreCorner) const; bool isCanreach(const Point *point,const Point *target,bool isIgnoreCorner) const; //判断某点是否可以用于下一步判断 Point *isInList(const std::list<Point *> &list,const Point *point) const; //判断开启/关闭列表中是否包含某点 Point *getLeastFpoint(); //从开启列表中返回F值最小的节点 //计算FGH值 int calcG(Point *temp_start,Point *point); int calcH(Point *point,Point *end); int calcF(Point *point); private: std::vector<std::vector<int>> maze; std::list<Point *> openList; //开启列表 std::list<Point *> closeList; //关闭列表 }; |
Astar.cpp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 | #include <math.h> #include "Astar.h" void Astar::InitAstar(std::vector<std::vector<int>> &_maze) { maze=_maze; } int Astar::calcG(Point *temp_start,Point *point) { int extraG=(abs(point->x-temp_start->x)+abs(point->y-temp_start->y))==1?kCost1:kCost2; int parentG=point->parent==NULL?0:point->parent->G; //如果是初始节点,则其父节点是空 return parentG+extraG; } int Astar::calcH(Point *point,Point *end) { //用简单的欧几里得距离计算H,这个H的计算是关键,还有很多算法,没深入研究^_^ return sqrt((double)(end->x-point->x)*(double)(end->x-point->x)+(double)(end->y-point->y)*(double)(end->y-point->y))*kCost1; } int Astar::calcF(Point *point) { return point->G+point->H; } Point *Astar::getLeastFpoint() { if(!openList.empty()) { auto resPoint=openList.front(); for(auto &point:openList) if(point->F<resPoint->F) resPoint=point; return resPoint; } return NULL; } Point *Astar::findPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner) { openList.push_back(new Point(startPoint.x,startPoint.y)); //置入起点,拷贝开辟一个节点,内外隔离 while(!openList.empty()) { auto curPoint=getLeastFpoint(); //找到F值最小的点 openList.remove(curPoint); //从开启列表中删除 closeList.push_back(curPoint); //放到关闭列表 //1,找到当前周围八个格中可以通过的格子 auto surroundPoints=getSurroundPoints(curPoint,isIgnoreCorner); for(auto &target:surroundPoints) { //2,对某一个格子,如果它不在开启列表中,加入到开启列表,设置当前格为其父节点,计算F G H if(!isInList(openList,target)) { target->parent=curPoint; target->G=calcG(curPoint,target); target->H=calcH(target,&endPoint); target->F=calcF(target); openList.push_back(target); } //3,对某一个格子,它在开启列表中,计算G值, 如果比原来的大, 就什么都不做, 否则设置它的父节点为当前点,并更新G和F else { int tempG=calcG(curPoint,target); if(tempG<target->G) { target->parent=curPoint; target->G=tempG; target->F=calcF(target); } } Point *resPoint=isInList(openList,&endPoint); if(resPoint) return resPoint; //返回列表里的节点指针,不要用原来传入的endpoint指针,因为发生了深拷贝 } } return NULL; } std::list<Point *> Astar::GetPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner) { Point *result=findPath(startPoint,endPoint,isIgnoreCorner); std::list<Point *> path; //返回路径,如果没找到路径,返回空链表 while(result) { path.push_front(result); result=result->parent; } return path; } Point *Astar::isInList(const std::list<Point *> &list,const Point *point) const { //判断某个节点是否在列表中,这里不能比较指针,因为每次加入列表是新开辟的节点,只能比较坐标 for(auto p:list) if(p->x==point->x&&p->y==point->y) return p; return NULL; } bool Astar::isCanreach(const Point *point,const Point *target,bool isIgnoreCorner) const { if(target->x<0||target->x>maze.size()-1 ||target->y<0&&target->y>maze[0].size()-1 ||maze[target->x][target->y]==1 ||target->x==point->x&&target->y==point->y ||isInList(closeList,target)) //如果点与当前节点重合、超出地图、是障碍物、或者在关闭列表中,返回false return false; else { if(abs(point->x-target->x)+abs(point->y-target->y)==1) //非斜角可以 return true; else { //斜对角要判断是否绊住 if(maze[point->x][target->y]==0&&maze[target->x][point->y]==0) return true; else return isIgnoreCorner; } } } std::vector<Point *> Astar::getSurroundPoints(const Point *point,bool isIgnoreCorner) const { std::vector<Point *> surroundPoints; for(int x=point->x-1;x<=point->x+1;x++) for(int y=point->y-1;y<=point->y+1;y++) if(isCanreach(point,new Point(x,y),isIgnoreCorner)) surroundPoints.push_back(new Point(x,y)); return surroundPoints; } |
main.cpp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | #include <iostream> #include "Astar.h" using namespace std; int main() { //初始化地图,用二维矩阵代表地图,1表示障碍物,0表示可通 vector<vector<int>> maze={ {1,1,1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,1,0,1,0,0,0,0,1}, {1,0,0,1,1,0,0,0,0,0,0,1}, {1,0,0,0,0,0,1,0,0,1,1,1}, {1,1,1,0,0,0,0,0,1,1,0,1}, {1,1,0,1,0,0,0,0,0,0,0,1}, {1,0,1,0,0,0,0,1,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1,1,1} }; Astar astar; astar.InitAstar(maze); //设置起始和结束点 Point start(1,1); Point end(6,10); //A*算法找寻路径 list<Point *> path=astar.GetPath(start,end,false); //打印 for(auto &p:path) cout<<'('<<p->x<<','<<p->y<<')'<<endl; system("pause"); return 0; } |
运行结果










