曲线拟合
使用MATLAB实现最小二乘法,首先给出今天重点使用的两个函数。
p=polyfit(x,y,n):最小二乘法计算拟合多项式系数。x,y为拟合数据向量,要求维度相同,n为拟合多项式次数。返回p向量保存多项式系数,由最高次向最低次排列。
y=polyval(p,x):计算多项式的函数值。返回在x处多项式的值,p为多项式系数,元素按多项式降幂排序。
比如想拟合下面这组数据
x=[9,13,15,17,18.6,20,23,29,31.7,35];
y=[-8,-6.45,-5.1,-4,-3,-1.95,-1.5,-0.4,0.2,-0.75];
先用matlab将这组离散点画出来,
plot(x,y,'o')
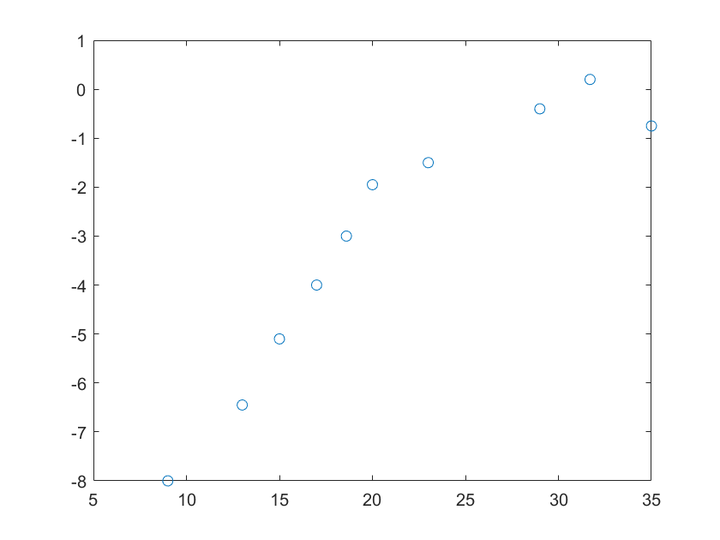
----------------------------------------更新代码---------------------------------------------
嗯,大概这个样子,这时我们想使用一次函数拟合上述曲线,可使用以下代码
clear
x=[9,13,15,17,18.6,20,23,29,31.7,35];
y=[-8,-6.45,-5.1,-4,-3,-1.95,-1.5,-0.4,0.2,-0.75];
plot(x,y,'*r')
hold on
p1=polyfit(x,y,1)
y1=polyval(p1,x)
plot(x,y1,'b')
p2=polyfit(x,y,2)
y2=polyval(p2,x)
plot(x,y2,'c')
p3=polyfit(x,y,3)
y3=polyval(p3,x)
plot(x,y3,'m')
p5=polyfit(x,y,5)
y5=polyval(p5,x)
plot(x,y5,'k')
得到的结果是
p1=[0.2989,-9.4107]
所以得到的一次函数为
y1=0.2989*x-9.4107
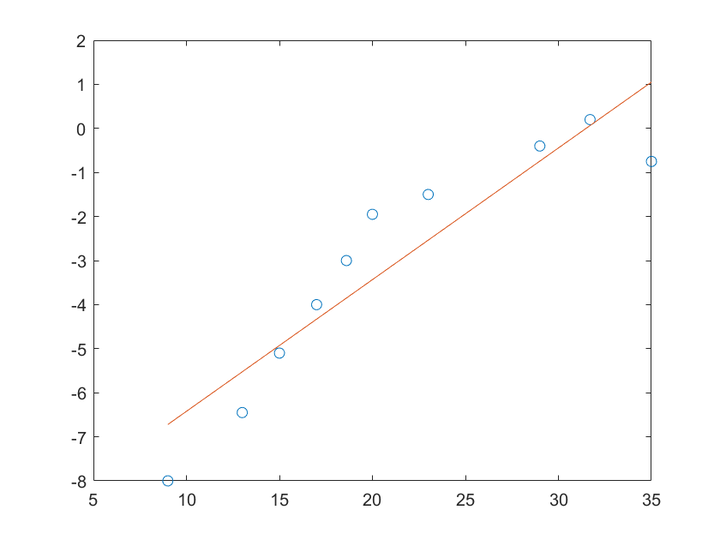
同理如果用二次函数拟合该曲线,得到的各项系数为
coefficient=[-0.0157 1.0037 -16.2817]
所以得到的二次函数为
y=-0.0157*x^2+1.0037*x-16.2817
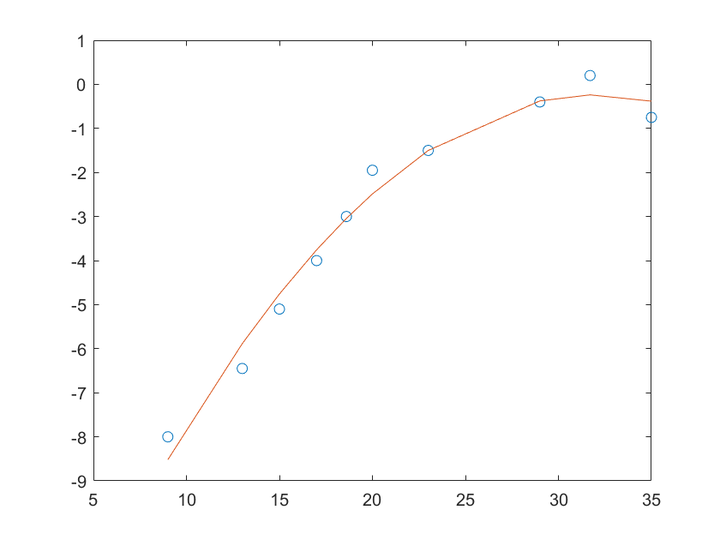
其他阶数依此类推。
但是使用polyfit(x,y,n)函数有一个注意事项:
向量x(其中元素作为自变量)中不重复的元素个数m,和拟合阶数k需要满足m>=k+1.简单分析:k阶拟合需要确定k+1个未知参数(如1阶拟合y = ax + b需要确定a和b两个参数),故而至少需要k+1个方程,故而需要至少k+1个不同的已知数对(x,y),由于函数中x只能对应一个y,故而需要至少k+1个不同的x
举个例子,比如说我们想用9阶多项式拟合上述曲线时,我们发现拟合的曲线是正常的,得到的各项系数也是正常的

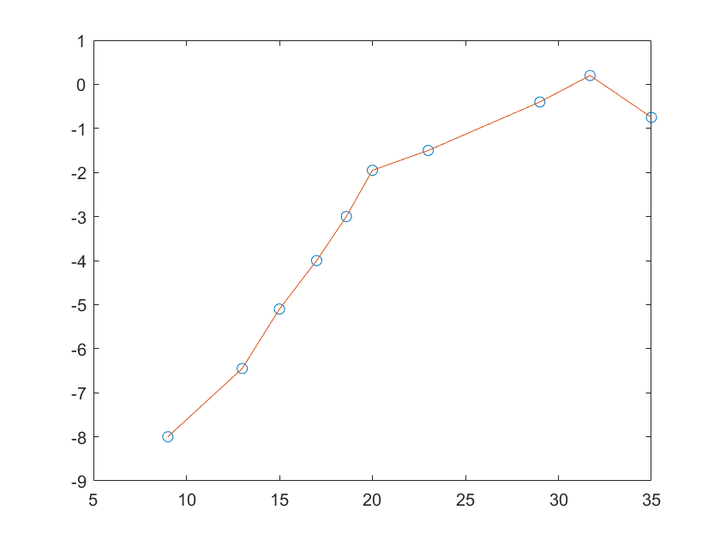
但是当我们用10阶多项式拟合曲线时,此时各项系数如下,得到的曲线如下


很明显出现了问题,所以使用polyfit(x,y,n)函数时要严格遵守上述事项。
====================================================
2.3 曲线拟合
MATLAB神经网络超级学习手册
在科学和工程领域,曲线拟合的主要功能是寻求平滑的曲线来最好地表现带有噪声的测量数据,从这些测量数据中寻求两个函数变量之间的关系或者变化趋势,最后得到曲线拟合的函数表达式y=f(x)。
一般来说,使用多项式进行数据拟合会出现数据振荡,而Spline插值的方法可以得到很好的平滑效果,但是关于该插值方法有太多的参数,不适合曲线拟合的方法。
同时,由于在进行曲线拟合的时候,已经认为所有测量数据中已经包含噪声,因此,最后的拟合曲线并不要求通过每一个已知数据点,衡量拟合数据的标准则是整体数据拟合的误差最小。
一般情况下,MATLAB的曲线拟合方法用的是“最小方差”函数,其中方差的数值是拟合曲线和已知数据之间的垂直距离。
2.3.1 多项式拟合
在MATLAB中,函数polyfit()采用最小二乘法对给定的数据进行多项式拟合,得到该多项式的系数。该函数的调用方式如下。
polyfit(x,y,n)
找到次数为n的多项式系数,对于数据集合{(xi, yi)},满足差的平方和最小。
[p,E]=polyfit(x,y,n)
返回同上的多项式P和矩阵E。多项式系数在向量p中,矩阵E用在polyval函数中来计算误差。
【例2-25】某数据的横坐标为x=[0.2 0.3 0.5 0.6 0.8 0.9 1.2 1.3 1.5 1.8],纵坐标为y=[1 2 3 5 6 7 6 5 4 1],对该数据进行多项式拟合。
解:代码如下。
x=[0.3 0.4 0.7 0.9 1.2 1.9 2.8 3.2 3.7 4.5];
y=[1 2 3 4 5 2 6 9 2 7];
p5=polyfit(x,y,5); %5阶多项式拟合
y5=polyval(p5,x);
p5=vpa(poly2sym(p5),5) %显示5阶多项式
p9=polyfit(x,y,9); %9阶多项式拟合
y9=polyval(p9,x);
figure; %画图显示
plot(x,y,'bo');
hold on;
plot(x,y5,'r:');
plot(x,y9,'g--');
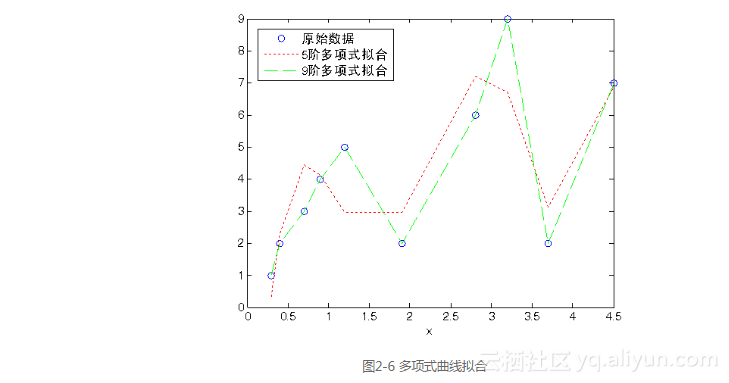
legend('原始数据','5阶多项式拟合','9阶多项式拟合');
xlabel('x');
ylabel('y');
运行程序后,得到的5阶多项式如下。
p5 =
0.8877*x^5 - 10.3*x^4 + 42.942*x^3 - 77.932*x^2 + 59.833*x - 11.673
运行程序后,得到的输出结果如图2-6所示。由图可以看出,使用5次多项式拟合时,得到的结果比较差。
当采用9次多项式拟合时,得到的结果与原始数据符合的比较好。当使用函数polyfit()进行拟合时,多项式的阶次最大不超过length(x)1。
**2.3.2 加权最小方差(WLS)拟合原理及实例
**所谓加权最小方差,就是根据基础数据本身各自的准确度的不同,在拟合的时候给每个数据以不同的加权数值。这种方法比前面所介绍的单纯最小方差方法要更加符合拟合的初衷。
对应N阶多项式的拟合公式,所需要求解的拟合系数需要求解线性方程组,其中线性方程组的系数矩阵和需要求解的拟合系数矩阵如下。
其对应的加权最小方差为表达式。
【例2-26】根据WLS数据拟合方法,自行编写使用WLS方法拟合数据的M函数,然后使用WLS方法进行数据拟合。
解:在M文件编辑器中输入下面的程序代码。
function [th,err,yi]=polyfits(x,y,N,xi,r)
%x,y为数据点系列,N为多项式拟合的系统,r为加权系数的逆矩阵。
M=length(x);
x=x(:);
y=y(:);
%判断调用函数的格式
if nargin==4
%当调用函数的格式为(x,y,N,r)
if length(xi)==M
r=xi;
xi=x;
%当调用函数的格式为(x,y,N,xi)
else
r=1;
end
%当调用格式为(x,y,N)
else if nargin==3
xi=x;
r=1;
end
%求解系数矩阵
A(:,N+1)=ones(M,1);
for n=N:-1:1
A(:,n)=A(:,n+1).*x;
end
if length(r)==M
for m=1:M
A(m,:)=A(m,:)/r(m);
y(m)=y(m)/r(m);
end
end
%计算拟合系数
th=(A\y)';
ye=polyval(th,x);
err=norm(y-ye)/norm(y);
yi=polyval(th,xi);
将上面代码保存为“polyfits.m”文件。
使用上面的程序代码,对基础数据进行LS多项式拟合。在MATLAB的命令窗口中输入下面的程序代码。
x=[-3:1:3]';
y=[1.1650 0.0751 -0.6965 0.0591 0.6268 0.3516 1.6961]';
[x,i]=sort(x);
y=y(i);
xi=min(x)+[0:100]/100*(max(x)-min(x));
for i=1:4
N=2*i-1;
[th,err,yi]=polyfits(x,y,N,xi);
subplot(2,2,i)
plot(x,y,'o')
hold on
plot(xi,yi,'-')
grid on
end
得到的拟合结果如图2-7所示。
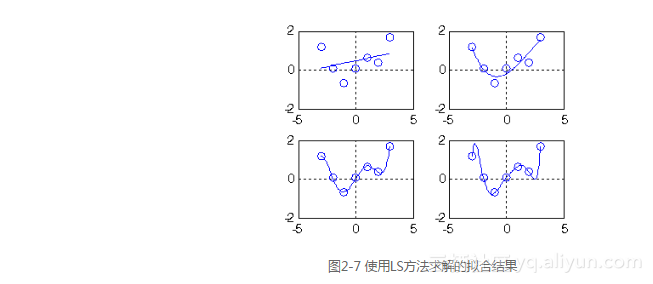
从上面的例子可以看出,LS方法其实是WLS方法的一种特例,相当于将每个基础数据的准确度都设为1,但是,自行编写的M文件和默认的命令结果不同,请仔细比较。
===================================================


