MATALAB中的fft、fftshift、fft2
傅立叶变换的分类:
https://www.cnblogs.com/21207-iHome/p/6048925.html
傅立叶级数:将周期性连续函数变换为离散频率点上的函数
傅立叶变换:将连续函数变换为连续频率的函数
离散时间傅立叶变换:将离散函数变换为连续频率的函数
离散傅立叶变换:将有限长离散函数变换为离散频率点上的函数
其中FFT是离散傅立叶变换的快速计算方法,适用于离散信号,并且注意变换后的点数与信号的采样点数一致。尽管可以将信号补0,但补0不能提高频域的分辨率。matlab中提供了函数fft做一维的FFT。
时域谱和频域谱是相互对应;时域的信号长度,决定频域的采样间隔,它们成导数关系;
时域中信号有N点,每点间隔dt,所以时域信号长度为N*dt;那么频谱每点的间隔F就是1/(N*dt)。(注:这里的采样间隔F=1/(N*dt)=Ws/N称为频谱分辨率,表示对x(n)在一个频谱周期内的N点等间隔采样)
傅立叶变换结果和原来信号有相同的点数,所以m=N,又第一点一定对应0频率,所以频域信号的很坐标就是(0:m-1)/(N*dt),这样就可以根据这个横坐标和频谱c,画出频谱图——plot((0:m-1)/(N*dt),c),在频谱图上可以根据峰值的位置的横坐标读出对应的频率。
%MATLAB自带的fft变换的应用
t_s=0;
t_e=10;
t_D=0.001;
f_Limit=1/t_D;
t=[t_s:t_D:t_e];
N=(t_e-t_s)/t_D+1; %共(t_e-t_s)/t_D +1个采样点
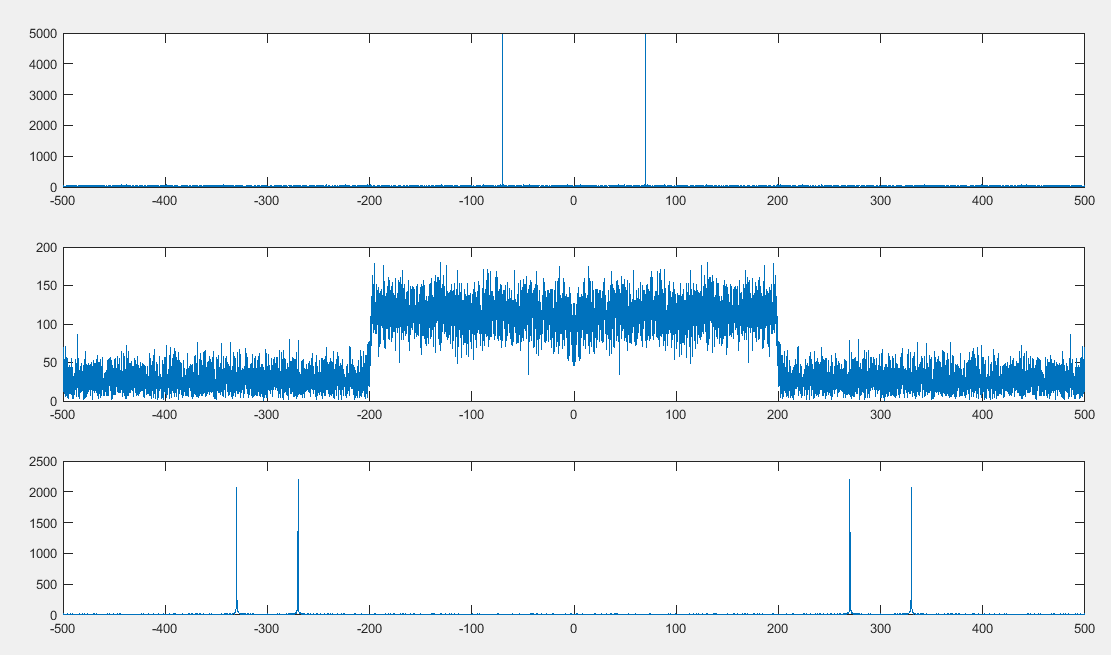
y1=sin(2*pi*70*t)+randn(1,N)*0.3; %加个随机噪声
y2=sin(2*pi*10*t.^2)+randn(1,N)*0.3; %加个随机噪声
y3=sin(2*pi*30*t).*cos(2*pi*300*t)+randn(1,N)*0.1; %加个随机噪声
F1=abs(fft(y1));
F2=abs(fft(y2));
F3=abs(fft(y3));
F1=fftshift(F1);
F2=fftshift(F2);
F3=fftshift(F3);
f_D=f_Limit/(N-1);
f=[0:f_D:f_Limit];
f=f-f_Limit/2;
subplot(3,1,1);plot(f,F1)
subplot(3,1,2);plot(f,F2)
subplot(3,1,3);plot(f,F3)
%编程实现DFT过程。
方法1:
%% 离散傅里叶变换DFT的过程 _cuichunlei 20200318
clear all
n=10
y=rand(1,n) %生成随机序列
tic %计时器
f_FFT=fft(y);
t_fft=toc;
tic
f_myDFT=zeros(1,n);
for f=0:n-1
for ii=0:n-1
f_myDFT(f+1)=f_myDFT(f+1)+y(ii+1)*exp(-i*2*pi*f*(ii)/(n))*1 ;
end
end
t_myDFT=toc;
f_FFT %MAT自带FFT算法
t_fft %自带算法耗费时间
f_myDFT %自己设计的DFT算法
t_myDFT %自己设计的算法耗费时间
%% 自己设计的离散傅里叶变换DFT算法的应用 _cuichunlei 20200318
clear all
t_s=0;
t_e=5;
t_D=0.001;
f_Limit=1/t_D;
t=[t_s: t_D :t_e];
n=(t_e-t_s)/t_D+1; %共(t_e-t_s)/t_D +1个采样点
%y=sin(2*pi*70*t)+randn(1,n)*0.3; %加个随机噪声
y=sin(2*pi*30*t).*cos(2*pi*300*t)+randn(1,n)*0.1;
%y=sin(2*pi*10*t.^2)+randn(1,n)*0.1;
tic
f_FFT=fft(y);
t_fft=toc;
tic
f_myDFT=zeros(1,n);
for f=0:n-1
for ii=0:n-1
f_myDFT(f+1)=f_myDFT(f+1)+y(ii+1)*exp(-i*2*pi*f*ii/n)*1 ;
end
end
t_myDFT=toc;
f_FFT
t_fft
f_myDFT
t_myDFT
f_FFT_v=abs(f_FFT);
f_FFT_v=fftshift(f_FFT_v);
f_myDFT_v=abs(f_myDFT);
f_myDFT_v=fftshift(f_myDFT_v);
f_D=f_Limit/(n-1);
f=[0: f_D :f_Limit];
f=f-f_Limit/2;
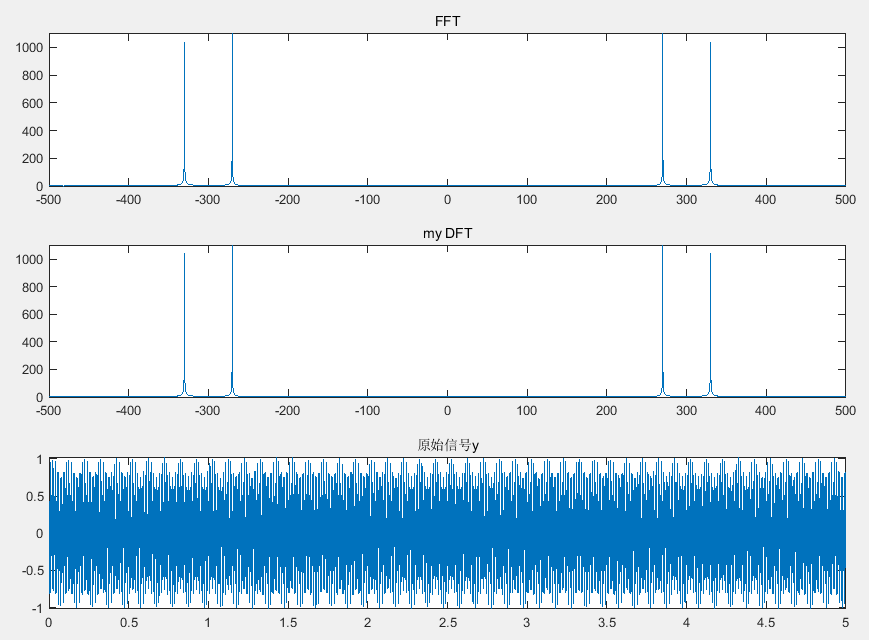
subplot(3,1,1); plot(f,f_FFT_v); title('FFT');
subplot(3,1,2); plot(f,f_myDFT_v); title('my DFT');
subplot(3,1,3); plot(t,y); title('原始信号y');
%二维傅里叶变换,图像DFT处理代码 _cuichunlei 20200319
clear all
pic=imread(' F:\bird_gray_small.jpg '); %读取自己的图像,尽量不要超过200*200
[m,n]=size(pic)
% pic=rand(5,5)
% [m,n]=size(pic)
tic %计时器
f_FFT=fft2(pic);
t_fft=toc;
pic=double(pic);
f_myDFT=zeros(m,n);
tic
for u=0:m-1 %没有优化处理,时间复杂度为n^4,可怕!
if rem(u,10)==0 %简易计数器,查看程序执行的进程。可以删掉这三行
u
end
for x=0:m-1
for v=0:n-1
for y=0:n-1
f_myDFT(u+1,v+1)=f_myDFT(u+1,v+1)+pic(x+1,y+1)*exp(-i*2*pi*u*x/m-i*2*pi*v*y/n)*1 ;
end
end
end
end
t_myDFT=toc;
f_FFT; f_myDFT;
t_fft
t_myDFT
f_FFT=fftshift(f_FFT);
f_FFT_v=abs(f_FFT);
f_FFT_v=mapminmax(f_FFT_v,0,1);
f_myDFT=fftshift(f_myDFT);
f_myDFT_v=abs(f_myDFT);
f_myDFT_v=mapminmax(f_myDFT_v,0,1);
subplot(1,2,1); imshow(f_FFT_v); title('FFT');
subplot(1,2,2); imshow(f_myDFT_v); title('my DFT'); %显示本文代码与matlab自带的fft2的一致性。
方法2:
clear all;
N=256;
dt=0.02;
n=0:N-1;
t=n*dt;
x=sin(2*pi*t);
m=N;
a=zeros(1,m);
b=zeros(1,m);
for k=0:m-1
for ii=0:N-1
a(k+1)=a(k+1)+2/N*x(ii+1)*cos(2*pi*k*ii/N);
b(k+1)=b(k+1)+2/N*x(ii+1)*sin(2*pi*k*ii/N);
end
c(k+1)=sqrt(a(k+1)^2+b(k+1)^2);
end
subplot(211); plot(t,x); title('原始信号'), xlabel('时间/t');
f=(0:m-1)/(N*dt);
subplot(212); plot(f,c) ; hold on
title('Fourier'); xlabel('频率/HZ'); ylabel('振幅');
ind=find(c==max(c),1,'first'); %寻找最大值的位置
%%%%%%% ind = find(X, k) 或ind = find(X, k, 'first')
% 返回第一个非零元素k的索引值(顺序)。
% k必须是一个正数,但是它可以是任何数字数值类型。
x0=f(ind); %根据位置得到横坐标(频率)
y0=c(ind); %根据位置得到纵坐标(幅度)
plot(x0,y0,'ro');hold off
%%%%%%% hold on 和hold off,是相对使用的.通常是一个图上画两个曲线进行比较。
% 前者的意思是,你在当前图的轴(坐标系)中画了一幅图,再画另一幅图时,原来的图还在,与新图共存,都看得到
% 后者表达的是,你在当前图的轴(坐标系)中画了一幅图,此时,状态是hold off,则再画另一幅图时,原来的图就看不到了,在轴上绘制的是新图,原图被替换了
text(x0+1,y0-0.1,num2str(x0,'频率=%f'));
% text(x,y,'string')在图形中指定的位置(x,y)上显示字符串string
二维图像的傅里叶逆变换:
%% 二维傅里叶逆变换
x=imread('F:\bird_gray.jpg'); %读入灰度图
y=fft2(x); %二维傅里叶变换
z=ifft2(y)/255; %二维傅里叶逆变换
subplot(2,1,1);imshow(x);
subplot(2,1,2);imshow(z);
%% 二维傅里叶逆变换 用于滤波
I=imread('F:\bird_gray.jpg');
figure(1);
imshow(I);
J=imnoise(I,'gaussian',0,0.02);
figure(2);
imshow(J);
J=double(J);
f=fft2(J); %采用傅里叶变换
g=fftshift(f); %数据局陈平衡
[M,N]=size(f);
n1=floor(M/2); %滤波半径
n2=floor(N/2);
d0=10;
for i=1:M
for j=1:N
d=sqrt((i-n1)^2+(j-n2)^2);
if d>=d0
h1=1;
h2=1+0.5;
else
h1=0;
h2=0.5;
end
g1(i,j)=h1*g(i,j);
g2(i,j)=h2*g(i,j);
end
end
g1=ifftshift(g1);
g1=uint8(real(ifft2(g1))); %显示理想高通滤波结果
figure(3);imshow(g1);
title('理想高通滤波结果')
g2=ifftshift(g2);
g2=uint8(real(ifft2(g2)));
figure(4);imshow(g2); %显示理想高通加强滤波结果
title('理想高通加强滤波结果')
利用matlab求图像均值和方差的几种方法
一、求均值
% 求一副灰度图像的均值
close all;
clear;
clc;
i=imread('d:/lena.jpg'); %载入真彩色图像
i=rgb2gray(i); %转换为灰度图
i=double(i); %将uint8型转换为double型,否则不能计算统计量
% avg1=mean(i,1); %列向量均值
% avg2=mean(i,2); %行向量均值
% avg3=mean(i); %列向量均值
[m,n]=size(i);
s=0;
for x=1:m
for y=1:n
s=s+i(x,y); %求像素值总和 s
end
end
%所有像素均值
a1=mean(mean(i)); %第一种方法:先计算列向量均值,再求总均值。
a2=mean2(i); %第二种方法:用函数mean2求总均值
a3=s/(m*n); %第三种方法:按公式计算,像素值总和除以像素个数。
a4=sum(sum(i))/(m*n); %第四种方法:也是按公式计算,但是用sum来求像素值总和。
二、求方差
% 求一副灰度图像的方差
close all
clear
clc;
i=imread('d:/lena.jpg'); %载入真彩色图像
i=rgb2gray(i); %转换为灰度图
i=double(i); %将uint8型转换为double型,否则不能计算统计量
% sq1=var(i,0,1); %列向量方差,第二个参数为0,表示方差公式分子下面是n-1,如果为1则是n
% sq2=var(i,0,2); %行向量方差
avg=mean2(i); %求图像均值
[m,n]=size(i);
s=0;
for x=1:m
for y=1:n
s=s+(i(x,y)-avg)^2; %求得所有像素与均值的平方和。
end
end
%求图像的方差
a1=var(i(:)); %第一种方法:利用函数var求得。
a2=s/(m*n-1); %第二种方法:利用方差公式求得
a3=(std2(i))^2; %第三种方法:利用std2求得标准差,再平方即为方差。
https://www.zhihu.com/zvideo/1380217944631283712
解释:什么是傅里叶级数?看看这个12分钟的模拟动画
二维傅里叶变换原理:
一维信号可以分解为多个正弦信号;二维信号(图像)也能够分解为多个正弦分量(条纹分量)
对于一幅M×N的图像,其傅里叶变换公式如下:
![[公式]](https://www.zhihu.com/equation?tex=F%5Cleft%28+u%2C+v%5Cright%29%3D%5Csum_%7Bx%3D0%7D%5E%7BM-1%7D%7B%5Csum_%7By%3D0%7D%5E%7BN-1%7D%7Bf%5Cleft%28+x%2C+y+%5Cright%29e%5E%7B-j2%5Cpi%5Cleft%28+%5Cfrac%7Bux%7D%7BM%7D%2B%5Cfrac%7Bvy%7D%7BN%7D+%5Cright%29%7D%7D%7D)
这里我们给一幅1200×1200的图像:

1、先来讨论一下指数部分
![[公式]](https://www.zhihu.com/equation?tex=e%5E%7B-j2%5Cpi%5Cleft%28+%5Cfrac%7Bux%7D%7B1200%7D%2B%5Cfrac%7Bvy%7D%7B1200%7D+%5Cright%29%7D%3D%5Ccos2%5Cpi%5Cleft%28%5Cfrac%7Bux%7D%7B1200%7D%2B%5Cfrac%7Bvy%7D%7B1200%7D+%5Cright%29-j%5Csin2%5Cpi%5Cleft%28%5Cfrac%7Bux%7D%7B1200%7D%2B%5Cfrac%7Bvy%7D%7B1200%7D+%5Cright%29)
指数部分可以分解为实部(余弦函数)、虚部(正弦函数)
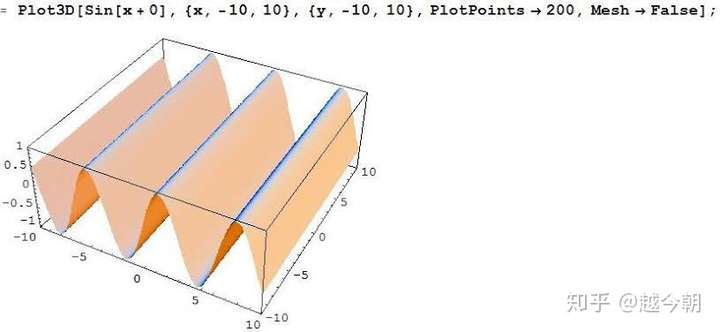
1)假设u=10,v=0,余弦函数和正弦函数的自变量为x,y(如下图:横轴坐标为x,纵轴坐标为y)。可以发现条纹方向是横向的。
 正弦图
正弦图 余弦图
余弦图
若u=0,v=10,条纹方向是纵向的
 正弦图
正弦图 余弦图
余弦图
若u=10,v=10:条纹方向为45°方向
 正弦图
正弦图 余弦图
余弦图
若u=10,v=17(≈10×根号3):条纹方向约为60°
 正弦图
正弦图 余弦图
余弦图
这里我们可以发现,条纹的方向是和向量(u/M, v/N)的方向平行的,文中举的例子因为M=N=1200,所以和向量(u,v)平行。
2)现在我们假设u=0,v=2, 5, 10
 v=2
v=2 v=5
v=5 v=10
v=10
可以发现:v为多少,就有多少道条纹;事实上条纹频率和 ![[公式]](https://www.zhihu.com/equation?tex=u%2Bv) 成正比 。
成正比 。
2、回到傅里叶变换公式部分
我们将公式中指数部分分解:
![[公式]](https://www.zhihu.com/equation?tex=F%5Cleft%28+u%2C+v%5Cright%29%3D%5Csum_%7Bx%3D0%7D%5E%7BM-1%7D%7B%5Csum_%7By%3D0%7D%5E%7BN-1%7D%7Bf%5Cleft%28+x%2C+y+%5Cright%29%5Cleft%28%5Ccos2%5Cpi%5Cleft%28%5Cfrac%7Bux%7D%7B1200%7D%2B%5Cfrac%7Bvy%7D%7B1200%7D+%5Cright%29-j%5Csin2%5Cpi%5Cleft%28%5Cfrac%7Bux%7D%7B1200%7D%2B%5Cfrac%7Bvy%7D%7B1200%7D+%5Cright%29%5Cright%29%7D%7D)
实部就可以看成:原图和余弦图的卷积,得到的值我们假设为 R(u, v)

虚部可以看成:原图和正弦图的卷积,得到的值我们假设为 I(u, v)

仔细观察能够发现:傅里叶变换公式和空间域的滤波公式十分接近,只不过是滤波模板的尺寸和原图一样大了而已,而u,v决定了模板的条纹形状。
3、幅值和相位
幅值表征了该条纹分量的幅度;相位 ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi) 表征了该条纹分量相对于原点的偏移量。确定u,v以后,没有偏移量的条纹(即相位为0的条纹分量)就是当前u,v确定的正弦条纹;若存在偏移量,就是正弦条纹沿条纹的法线方向偏移相应大小的偏移量(也可以理解成偏移“
表征了该条纹分量相对于原点的偏移量。确定u,v以后,没有偏移量的条纹(即相位为0的条纹分量)就是当前u,v确定的正弦条纹;若存在偏移量,就是正弦条纹沿条纹的法线方向偏移相应大小的偏移量(也可以理解成偏移“ ![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi%2F2%5Cpi) ”个周期)。
”个周期)。
不同的条纹分量的幅值: ![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7BR%5Cleft%28u%2Cv%5Cright%29%5E%7B2%7D%2BI%5Cleft%28u%2Cv%5Cright%29%5E%7B2%7D%7D)
不同的条纹分量的相位: ![[公式]](https://www.zhihu.com/equation?tex=arctan%5Cleft%28%5Cfrac%7BI%5Cleft%28u%2Cv%5Cright%29%7D%7BR%5Cleft%28u%2Cv%5Cright%29%7D%5Cright%29)
为什么可以这么计算,这个证明过程比较复杂,为了让大家直观的感受一下,这里举一个一维信号的例子:
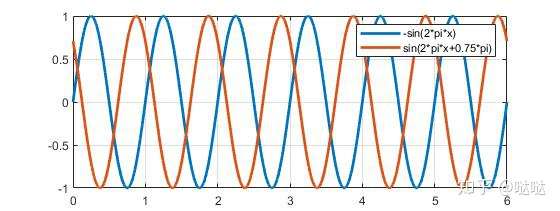
假设存在一正弦函数 ![[公式]](https://www.zhihu.com/equation?tex=%5Csin%282%5Cpi+x%2B0.75%5Cpi%29) ,假设我们知道该正弦函数的频率,但不知道该正弦函数的相位,为了得到该函数的相位,可以用正弦函数
,假设我们知道该正弦函数的频率,但不知道该正弦函数的相位,为了得到该函数的相位,可以用正弦函数 ![[公式]](https://www.zhihu.com/equation?tex=%5Csin%282%5Cpi+x%2B%5Cvarphi%29) 与之进行相关计算:
与之进行相关计算:
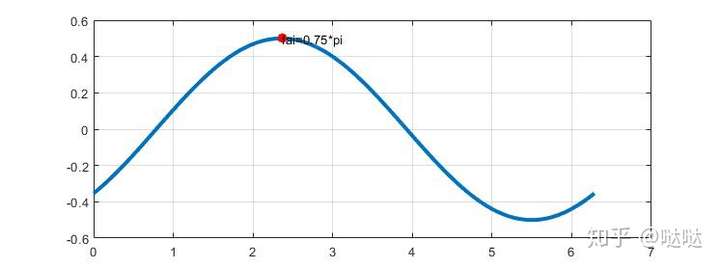
通过相关函数的最大值,我们可以确定该正弦函数的相位值为![[公式]](https://www.zhihu.com/equation?tex=%5Cvarphi%3D0.75%5Cpi)
除了这种方法能够得到相位值,还有没有别的方法呢?答案是有的!话不多说,直接上matlab程序,大家看程序理解吧!
P=0.75*pi; %偏移相位
B=0:0.00001:6;
T1=sin(2*pi*B); %正弦函数
T2=cos(2*pi*(B)); %余弦函数
T3=sin(2*pi*B+P); %添加偏移相位的函数
C1=sum(T3.*T3);
C2=sqrt((sum(T1.*T3))^2+(sum(T2.*T3))^2);
disp(C1);disp(C2);
disp(sum(T1.*T3)/sum(T2.*T3))
disp(tan(P))
>>3.0000e+05
3.0000e+05
-1.0000
-1.0000
可以看出不仅相位,幅值最终也相同。
链接:https://www.zhihu.com/question/29246532/answer/1035400862
一维傅里叶变换原理:
(a).周期函数,可以通过傅立叶级数画出频域图
(b).增长周期,频域图变得越来越密集
(c).,得到傅立叶变换,频域图变为连续的曲线
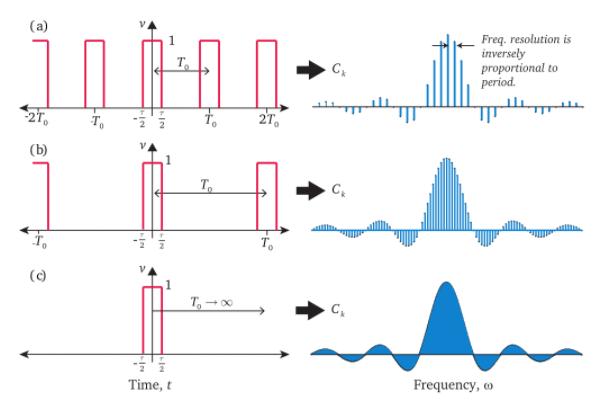

参考:
https://www.matongxue.com/madocs/712.html
https://www.matongxue.com/madocs/619.html
https://www.matongxue.com/madocs/473.html
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
图片的二维傅里叶变换的频域图:




总之,移频后的频谱图中心代表低频部分,四周代表高频部分,频谱图中的值代表能量,能量多代表原图中的这部分频率的多。
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度.在噪声点和图像边缘处的频率为高频。
傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数,傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。
傅立叶变换以前,图像(未压缩的位图)是由对在连续空间(现实空间)上的采样得到一系列点的集合,我们习惯用一个二维矩阵表示空间上各点,则图像可由z=f(x,y)来表示。由于空间是三维的,图像是二维的,因此空间中物体在另一个维度上的关系就由梯度来表示,这样我们可以通过观察图像得知物体在三维空间中的对应关系。
为什么要提梯度?因为实际上对图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。
一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。
==============================================
总得来说,低频分量(低频信号)代表着图像中亮度或者灰度值变化缓慢的区域,也就是图像中大片平坦的区域,描述了图像的主要部分。。高频分量(高频信号)对应着图像变化剧烈的部分,也就是图像的边缘(轮廓)或者噪声以及细节部分。
之所以说噪声也对应着高频分量,是因为图像噪声在大部分情况下都是高频的。
低频分量:主要对整幅图像强度的综合度量。高频分量:主要是对图像边缘和轮廓的度量。而人眼对高频分量比较敏感。
我们试着用傅立叶变换站在另外一个角度观察图像,将图像从灰度分布转化到频率分布(频谱图)上去观察图像的特征。需要了解的是,图像进行二维傅立叶变换之后得到的频谱图,就是图像梯度的分布图。具体的,傅立叶频谱图上我们能看到明暗不一的亮点,实际是图像上某一点与邻域点差异的强弱,即梯度的大小。
所以说,如果一幅图像的各个位置的强度大小相等,则图像只存在低频分量。从图像的频谱图上看,只有一个主峰,且位于频率为零的位置.。需要提一句的是,图像的频谱图可以由傅里叶变换得到。
如果一幅图像的各个位置的强度变化剧烈,则图像不仅存在低频分量,同时也存在多种高频分量。从图像的频谱上看,不仅有一个主峰,同时也存在多个旁峰。可以这样理解:图像中的低频分量就是图像中梯度较小的部分,高频分量则相反。
从直方图上看,低频分量对应直方图内大块区域,而小块或者离散的区域就是高频分量。这说明低频分量占据了图像的主要部分。
从二维函数上理解,变化剧烈的地方就是高频分量,变化少的地方就是低频分量。
总结
总的来说,其实低频分量和高频分量只是一种相对的概念。对于二维信号来说,即图像,低频分量和高频分量与像素值的大小无关。比如一张全白的图像,从像素值的意义上来说它的值全是255,在uint8中已经是像素的最大值,但是它却只有低频分量而没有高频分量。因为每一个像素点(目标像素点)的周围都不具有对比度,即周围像素点没有相对于目标像素点的像素值大或者小。
===============================================
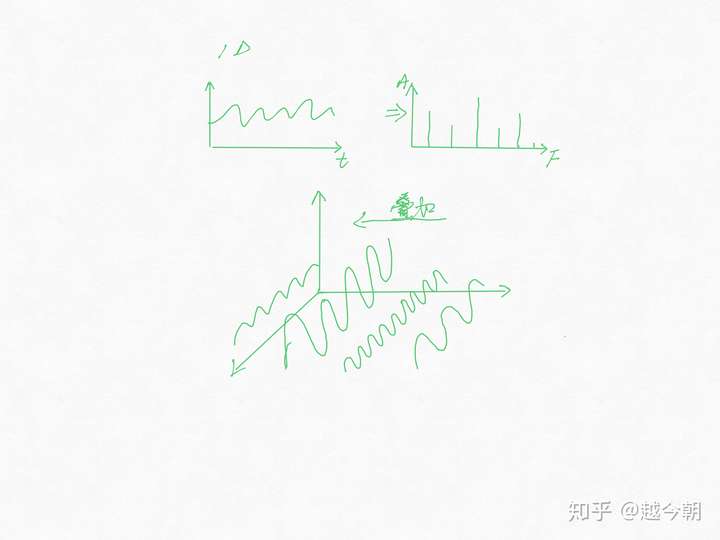
先是一维变换的物理意义
最后的图频率画的有问题 不想重画了各位将就看 不影响核心意思
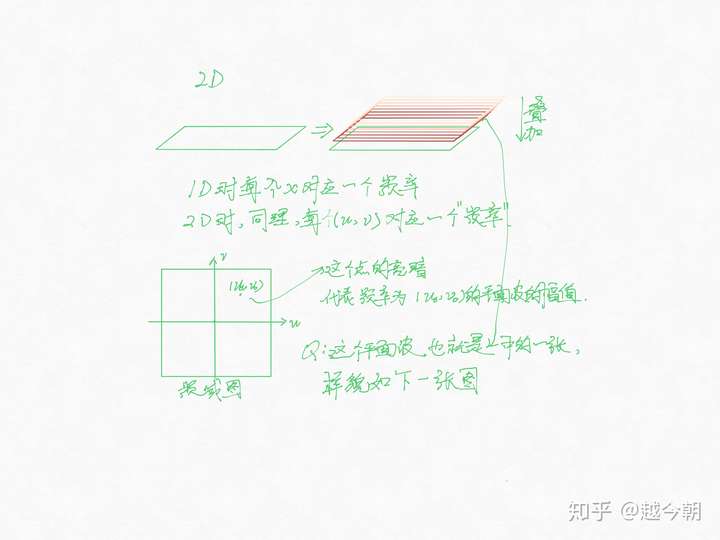
 Google上找的如果侵权联系我删除
Google上找的如果侵权联系我删除

仅讨论物理意义 之后理解公式就容易多了
放个结论
二维傅立叶变换 不同的坐标对应的点 代表不同的平面波 包括频率和角度
频率表示的是图像灰度变化的程度
频域图的亮暗代表能量高低 既平面波的幅值
一般正中心是原点 正中心比较亮 周围暗说明图片还是由较多灰度变化低的平面波叠加而成的
%%%%%%%%%%%%%% https://www.zhihu.com/question/26969067/answer/567804862
频谱中的亮线 证明空域中有 与亮线方向垂直的边缘
因为频谱上每个点所代表的正弦波方向是固定的 x轴上的正弦波就是传播方向向x轴的波
空域的一条亮线 如果是竖直 就是x方向有突变 换到一维 就像一个方波 理论上是无穷多个不同频率正弦波的叠加 从小到大都有
所以x轴上 所有点 即频率都有值 结果是一条亮线 在频域
但空域上 虽然我们知道变化本身在x方向,这条边缘却是在y方向的 所以有了垂直关系
=============================================================
图像熵计算
信息熵:
利用信息论中信息熵概念,求出任意一个离散信源的熵(平均自信息量)。自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。一条信息的信息量和它的不确定性有着直接的关系。所发出的消息不同,它们所含有的信息量也就不同。任何一个消息的自信息量都代表不了信源所包含的平均自信息量。不能作为整个信源的信息测度,因此定义自信息量的数学期望为信源的平均自信息量:

信息熵的意义:信源的信息熵H是从整个信源的统计特性来考虑的。它是从平均意义上来表征信源的总体特性的。对于某特定的信源,其信息熵只有一个。不同的信源因统计特性不同,其熵也不同。信息熵一般用符号H表示,单位是比特。变量的不确定性越大,熵也就越大。
图像熵:
1.一元灰度熵
图像熵是一种特征的统计形式,它反映了图像中平均信息量的多少。图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量,令Pi 表示图像中灰度值为i的像素所占的比例,则定义灰度图像的一元灰度熵为:

其中Pi是某个灰度在该图像中出现的概率,可由灰度直方图获得。
1.二维熵
图像的一维熵可以表示图像灰度分布的聚集特征,却不能反映图像灰度分布的空间特征,为了表征这种空间特征,可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。选择图像的邻域灰度均值作为灰度分布的空间特征量,与图像的像素灰度组成特征二元组,记为( i, j ),其中i 表示像素的灰度值(0 <= i <= 255),j 表示邻域灰度均值(0 <= j <= 255):

上式能反应某像素位置上的灰度值与其周围像素灰度分布的综合特征,其中f(i, j)为特征二元组(i, j)出现的频数,N 为图像的尺度,定义离散的图像二维熵为:

构造的图像二维熵可以在图像所包含信息量的前提下,突出反映图像中像素位置的灰度信息和像素邻域内灰度分布的综合特征。
========================================================
这里我们主要要讲的是二维图像傅里叶变换,但是我们首先来看一张很厉害的一维傅里叶变换动图。
妈耶~厉害哇!它把时域和频域解释的很清楚!
什么!你看不懂!
简单点说就是:所有的波都可以用很多个正弦波叠加表示。
然而这些波又可以通过频率、幅值和相位来表示。这样你就可以从左边那张图中时域的视角转化为咱们高大上的频域视角啦。
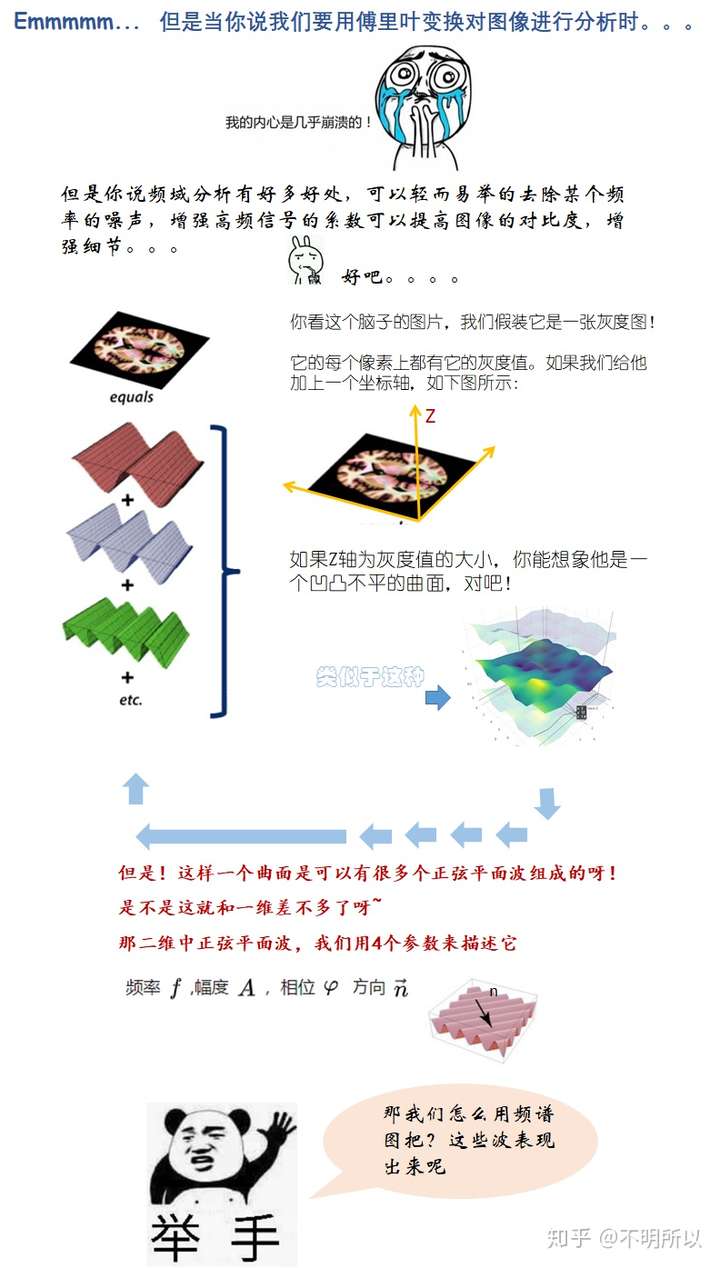
那首先来看一个例子~
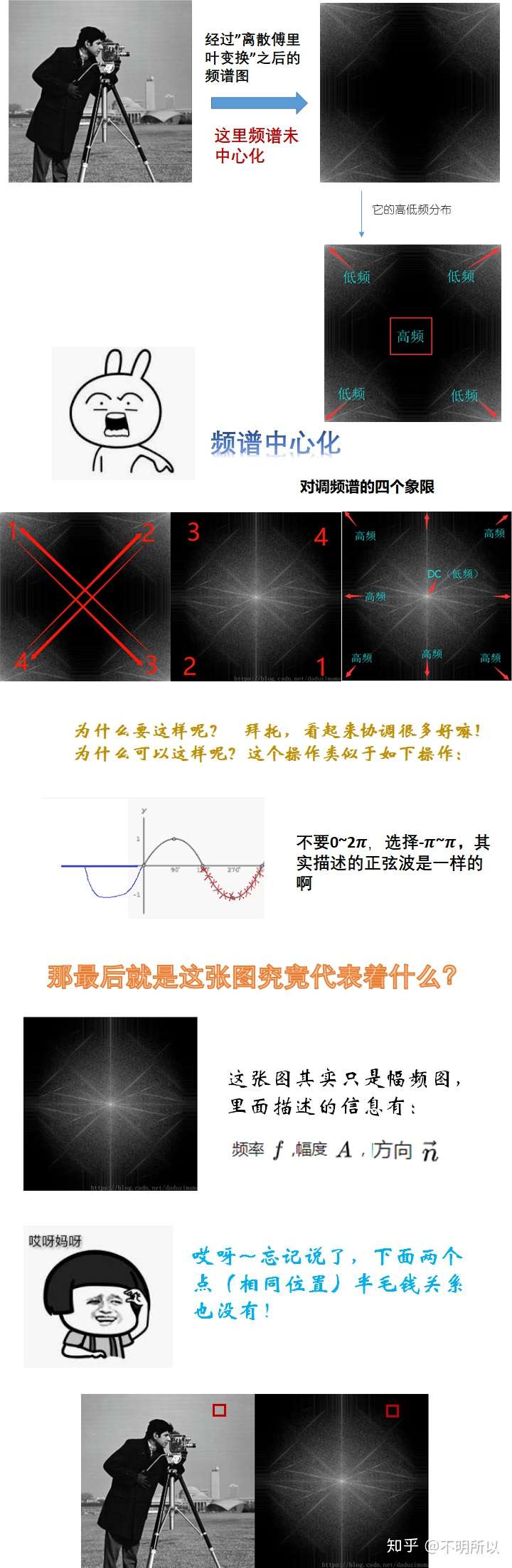
其实右边图的每一个点,可以理解为它在描述一种平面波。
那…其实还是有两个点之间还是有半分钱关系的,右边点所描述的波是构成左边点的无数个波面中的其中一个。
右边图中,每一个点:
1)它到中点的距离描述的是频率
2)中点到它的方向,是平面波的方向
3)那一点的灰度值描述的是它的幅值
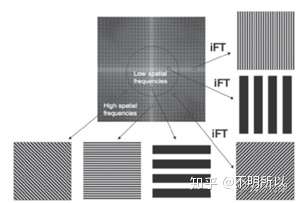


=====================================================
下面这篇文章将从直观理解的角度解释傅里叶变换中的不确定性原理。
其中主要参考了这个视频:非常推荐!
https://www.bilibili.com/video/av20317906?t=1073www.bilibili.com
傅里叶变换中的不确定性原理其实就是时域和频域的不确定性原理,即一个信号不可能同时在频域和时域具有任意小的分辨率。通俗来说就是,对于一个信号,时域越长,频域越短(集中);时域越短,频域越长。
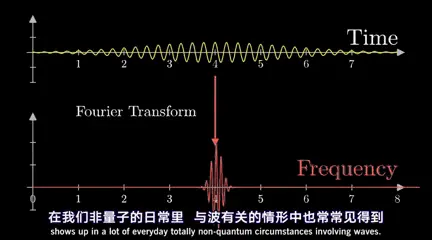
1.不确定性原理的实例
如果![[公式]](https://www.zhihu.com/equation?tex=f%5Cleft%28+t+%5Cright%29+%5Cleftrightarrow+F%5Cleft%28+s+%5Cright%29+) ,那么
,那么 ![[公式]](https://www.zhihu.com/equation?tex=f%5Cleft%28+at+%5Cright%29+%5Cleftrightarrow+%5Cfrac%7B1%7D%7B%5Cleft%7C+a+%5Cright%7C%7DF%5Cleft%28+%5Cfrac%7Bs%7D%7Ba%7D+%5Cright%29+) 。从这个公式中也可以看出,频域和时域的变换关系是相反的。
。从这个公式中也可以看出,频域和时域的变换关系是相反的。
以高斯函数为例:
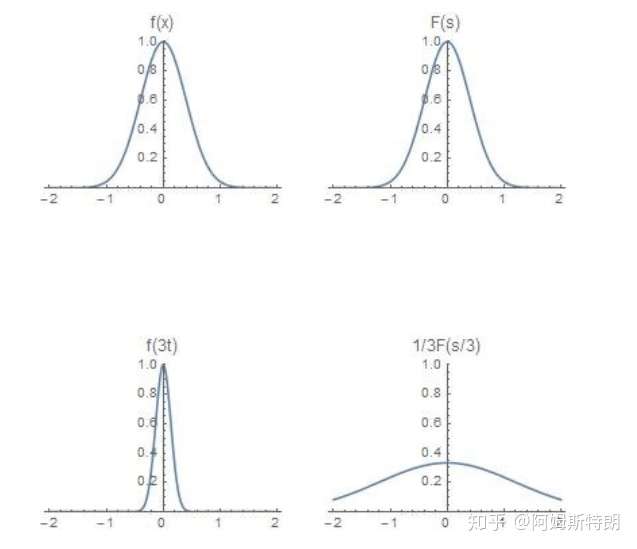 a=3,时域收缩,频域扩展
a=3,时域收缩,频域扩展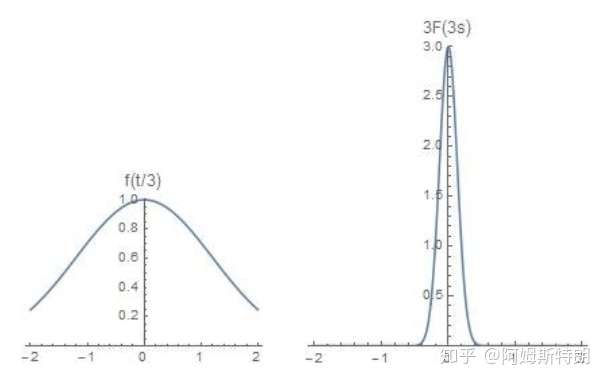 a=1/3,时域扩展,频域收缩
a=1/3,时域扩展,频域收缩
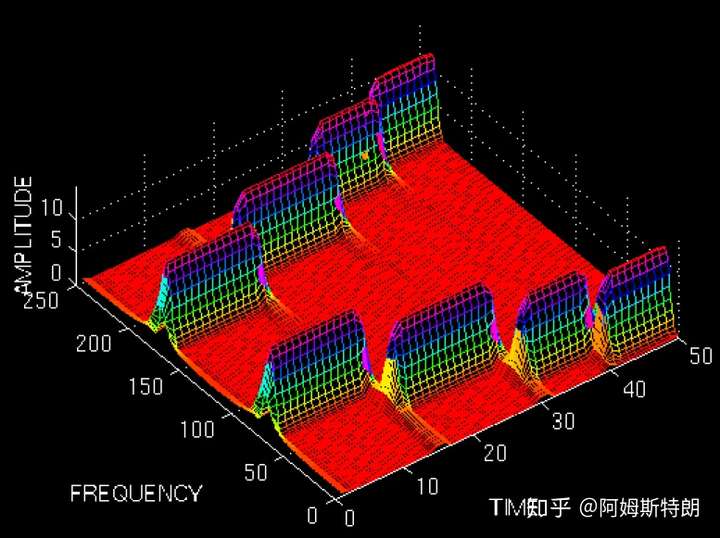 时域分辨率高,但是频域分辨率低(厚)
时域分辨率高,但是频域分辨率低(厚)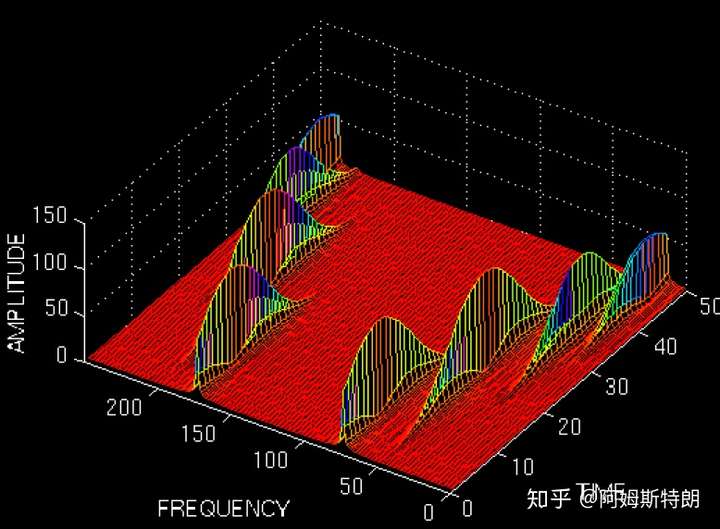 频域分辨率高(薄),但是时域有重叠
频域分辨率高(薄),但是时域有重叠
2.时域频域不确定性原理的解释
考虑两个汽车在路上以差不多的频率闪灯。在最开始的时候,你其实并不能很确定的判断他们闪灯的频率是否相等;因为如果频率相差很小,在比较短的时间里,你是看不出来的。但是随着观测的时间变长,如果他们还是以相似的频率闪动话,你就越能确定他们的频率是一样的。
这就好比两个人跑步,一个人200m/min;另一个人201m/min,观测一分钟只有1m的差距。但是随着观测时间变长,两人之间的差距也越来越大。
两个频率相近的信号也是如此:在时域中,开始时比较相似,随时间变长,两者的差距越来越明显。
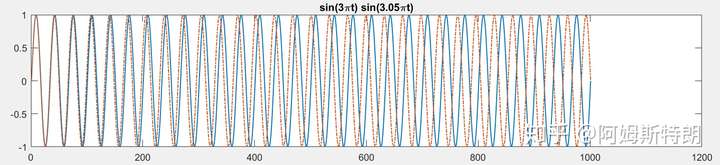
下面我们在频域中观察两个频率相近的信号,一个为 ![[公式]](https://www.zhihu.com/equation?tex=%5Comega%3D3%5Cpi) ,一个
,一个 ![[公式]](https://www.zhihu.com/equation?tex=%5Comega%3D3.15%5Cpi) 。发现时域较短时,频域中两个峰值会融合;时域较长时两个峰值则会分开。
。发现时域较短时,频域中两个峰值会融合;时域较长时两个峰值则会分开。
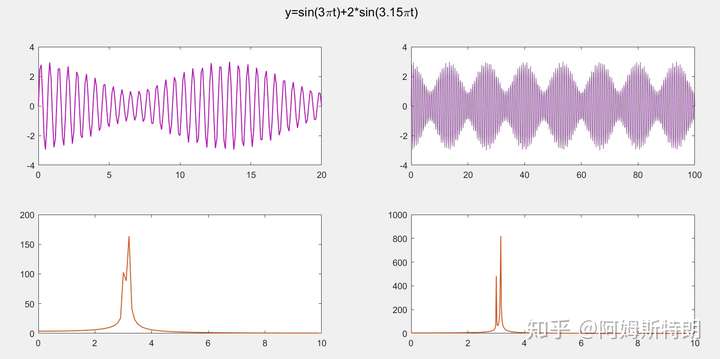
我们知道,傅里叶变换是将信号分解为若干个三角基之和,而求基向量的系数的时候需要用内积操作。我们前面说过,如果一个信号比较短,那么在频域中,其相似频率的信号与其本身相差不大。(例如3Hz和3.1Hz的信号在时间短的情况下相差不大)所以对信号进行分解时,所求得某个基向量与其相邻基向量的系数就会相差不大,(例如3Hz时为1,2.9Hz、3.1Hz的系数都是0.8)。因此这种情况下,频谱会出现分散。
而当信号很长时,频率稍有一点不同,也可以明显的体现出来,这时候内积求得的系数差距就会较大。(例如3Hz时为1,2.9Hz、3.1Hz的系数都是0.2),这种情况下,频谱比较集中。
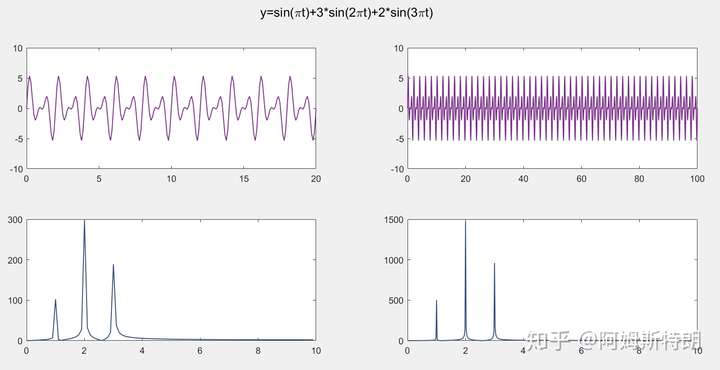
因为傅里叶变换是以三角基为基向量的分解,而三角基是无限长的,覆满了这个时域。所以一个信号时域越长,就有越多的信息来进行投影操作,所得的频域信息就越准确,分辨率就越高。
3.与海森堡不确定性原理的关系
前面我们大致说了一下,傅里叶变换中不确定性的现象和原因。但它和著名的海森堡不确定性原理有什么关系呢?其实二者是同一个事物。
德布罗意波![[公式]](https://www.zhihu.com/equation?tex=%5Crightarrow) 物质是波
物质是波
 德布罗意
德布罗意
物质波的概念最先由法国物理学家路易·维克多·德布罗意提出。他指出,任何物质都可以看作是波的存在。对于一个微观粒子来说,它在空间中没有确定的位置,它在空间中某个地方出现有一定的概率。描述粒子在空间中分布的概率密度函数就是波函数。
量子力学基本关系 ![[公式]](https://www.zhihu.com/equation?tex=p%3Dh%2F%5Clambda%3Dhf%2Fc)
在量子力学,粒子的动量是由其波长决定的,而波长又由频率决定,所以粒子的动量就正比于其波函数的频率。
所以,本质上,粒子的波函数与波函数频率的关系就是我们前面说过的时域和频域的关系。
因此,一个粒子的位置越确定,其波函数就越集中,所以波函数的频谱就越分散,动量就越不确定。
而实际上,量子力学中位置和动量的关系就是一个傅里叶变换对的关系。
![[公式]](https://www.zhihu.com/equation?tex=%5CvarPsi+%5Cleft%28+x+%5Cright%29+%3D%5Cleft%28+2%5Cpi+%5Cright%29+%5E%7B-%5Ctext%7B3%2F%7D2%7D%5Cint_%7BE%5E3%7D%7B%5Ctilde%7B%5CvarPsi%7D%5Cleft%28+P+%5Cright%29+e%5E%7BiP%5Ccdot+x%2F%5Chbar%7Dd%5E3P%7D+%5C%5C+%5Ctilde%7B%5CvarPsi%7D%5Cleft%28+p+%5Cright%29+%3D%5Cleft%28+2%5Cpi+%5Cright%29+%5E%7B-%5Ctext%7B3%2F%7D2%7D%5Cint_%7BE%5E3%7D%7B%5CvarPsi+%5Cleft%28+X+%5Cright%29+e%5E%7Bip%5Ccdot+X%2F%5Chbar%7Dd%5E3X%7D++)
如何从数学角度证明傅里叶变换中的不确定性呢?请看我的同系列第二篇文章。
阿姆斯特朗:傅里叶变换中的不确定性原理(二)zhuanlan.zhihu.com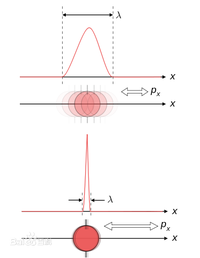













成正比 。


表征了该条纹分量相对于原点的偏移量。确定u,v以后,没有偏移量的条纹(即相位为0的条纹分量)就是当前u,v确定的正弦条纹;若存在偏移量,就是正弦条纹沿条纹的法线方向偏移相应大小的偏移量(也可以理解成偏移“
”个周期)。

,假设我们知道该正弦函数的频率,但不知道该正弦函数的相位,为了得到该函数的相位,可以用正弦函数
与之进行相关计算:






















,那么
。从这个公式中也可以看出,频域和时域的变换关系是相反的。





,一个
。发现时域较短时,频域中两个峰值会融合;时域较长时两个峰值则会分开。


物质是波





