模拟退火算法原理
模拟退火(simulated annealing,SA)算法的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。模拟退火法是一种通用的优化算法,其物理退火过程由以下三部分组成:
(1)加温过程。其目的是增强粒子的热运动,使其偏离平衡位置。当温度足够高时,固体将熔为液体,从而消除系统原先存在的非均匀状态。
(2)等温过程。对于与周围环境交换热量而温度不变的封闭系统,系统状态的自发变化总是朝自由能减少的方向进行的,当自由能达到最小时,系统达到平衡状态。
(3)冷却过程。使粒子热运动减弱,系统能量下降,得到晶体结构。
其中,加温过程对应算法的设定初温,等温过程对应算法的Metropolis抽样过程,冷却过程对应控制参数的下降。这里能量的变化就是目标函数,要得到的最优解就是能量最低态。Metropolis准则是SA算法收敛于全局最优解的关键所在,Metropolis准则以一定的概率接受恶化解,这样就使算法跳离局部最优的陷阱。
模拟退火算法为求解传统方法难处理的TSP问题提供了一个有效的途径和通用框架,并逐渐发展成一种迭代自适应启发式概率性搜索算法。模拟退火算法可以用以求解不同的非线性问题,对不可微甚至不连续的函数优化,能以较大概率求得全局优化解。该算法还具有较强的鲁棒性、全局收敛性、隐含并行性及广泛的适应性,并且能处理不同类型的优化设计变量(离散的、连续的和混合型的),不需要任何的辅助信息,对目标函数和约束函数没有任何要求。利用Metropolis算法并适当地控制温度下降过程,在优化问题中具有很强的竞争力,本章主要研究基于模拟退火算法的TSP算法。
算法步骤
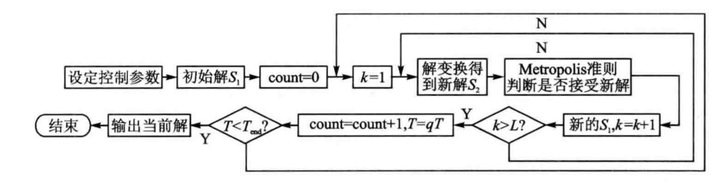
SA算法实现过程如下(以最小化问题为例):
【1】初始化:取初始温度 足够大,令
,任取初始解
,确定每个
时的迭代次数,即Metropolis链长
。
【2】对当前温度 和
,重复步骤【3】-【6】。
【3】对当前解 随机扰动产生一个新解
。
【4】计算 的增量
,其中
为
的代价函数。
【5】若 ,则接受
作为新的当前解,即
;否则计算
的接受概率
,即随机产生
区间上均匀分布的随机数rand,若
,也接受
作为新的当前解,
;否则保留当前解
。
【6】如果满足终止条件Stop,则输出当前解 为最优解,结束程序。终止条件Stop通常为:在连续若干个Metropolis链中新解
都没有被接受时终止算法,或是设定结束温度。否则按衰减函数衰减
后返回步骤【2】。
以上步骤称为Metropolis过程。逐渐降低控制温度,重复Metropolis过程,直至满足结束准则Stop,求出最优解。
TSP问题(旅行商问题)
TSP问题是典型的NP完全问题,即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长,到目前为止还未找到一个多项式时间的有效算法。
TSP问题可描述为:已知 个城市相互之间的距离,某一旅行商从某个城市出发访问每个城市一次且仅一次,最后回到出发城市,如何安排才使其所走路线最短。简言之,就是寻找一条最短的遍历
个城市的路径,或者说搜索自然子集
(
的元素表示对
个城市的编号)的一个排列
,使
取最小值,其中 表示城市
到城市
的距离。
TSP问题并不仅仅是旅行商问题,其他许多的NP完全问题也可以归结为TSP问题,如邮路问题、装配线上的螺母问题和产品的生产安排问题等,使得TSP问题的有效求解具有重要意义。
例题
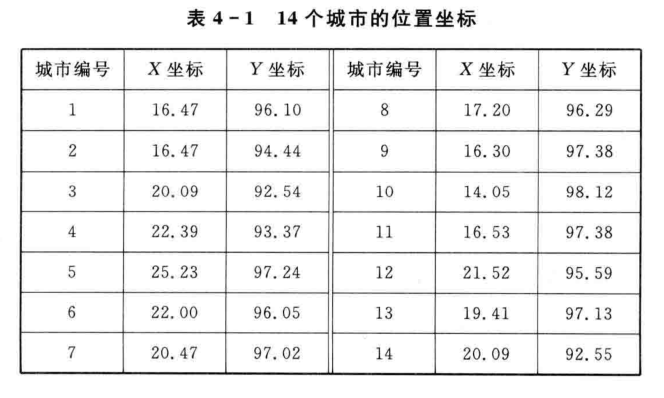
假定14个城市的位置坐标如表所列。寻找出一条最短的遍历14个城市的路径。
算法实现:
【1】设置主要控制参数
降温速率 、初始温度
、结束温度
以及链长
。
【2】初始解
对于 个城市的TSP问题,得到的解就是对
的一个排序,其中每个数字为对应城市的编号,如对10个城市的TSP问题
,则
就是一个合法的解,采用产生随机排列的方法产生一个初始解
。
【3】解变换生成新解
通过对当前解 进行变换,产生新的路径数组即新解,这里采用的变换是产生随机数的方法来产生将要交换的两个城市,用二邻域变换法产生新的路径,即新的可行解
。
例如 时,产生两个
范围内的随机整数
和
,确定两个位置,将其对换位置,如

得到的新解为

【4】Metropolis准则
若路径长度函数为 ,则当前解的路径为
,新解的路径为
,路径差为
,则Metropolis准则为
如果 ,则以概率1接受新的路径;否则以概率
接受新的路径。
【5】降温
利用降温速率 进行降温,即
,若
小于结束温度,则停止迭代输出当前状态,否则继续迭代。
程序实现
1.计算距离矩阵
利用给出的N个城市的坐标,算出N个城市的两两之间的距离,得到距离矩阵 。
TSP_Distance.m
function distance = TSP_Distance(position_coordinates) % 计算两两城市之间的距离 %输入 position_coordinates 各城市的位置坐标 %输出 distance 两两城市之间的距离 row = size(position_coordinates,1); distance = zeros(row,row); for i = 1:row for j = i+1:row distance(i,j) = ((position_coordinates(i,1)-position_coordinates(j,1))^2+(position_coordinates(i,2)-position_coordinates(j,2))^2)^0.5; distance(j,i) = distance(i,j); end end
2.初始解
初始解的产生直接使用MATLAB自带的函数randperm。如城市个数为N,则产生初始解:
S1 = randperm(N); % randperm返回行向量,其中包含从1到n(包括两者)之间的整数随机置换 % 随机产生一个初始路线
3.生成新解
TSP_New_Solution.m
function S2 = TSP_New_Solution(S1) % 输入 % S1:当前解 % 输出 % S2:新解 N = length(S1); S2 = S1; a = round(rand(1,2)*(N-1) + 1); %产生两个随机位置 用来交换 W = S2(a(1)); S2(a(1)) = S2(a(2)); S2(a(2)) = W; %得到一个新路线
4.Metropolis准则函数
TSP_Metropolis.m
function [S,R] = TSP_Metropolis(S1,S2,distance,T) % 输入 % S1: 当前解 % S2: 新解 % distance: 距离矩阵(两两城市的之间的距离) % T: 当前温度 % 输出 % S: 下一个当前解 % R: 下一个当前解的路线距离 % fS1 = TSP_Feasible_Solution_Path_Length(distance,S1); %计算路线长度 N = length(S1); %得到城市的个数 fS2 = TSP_Feasible_Solution_Path_Length(distance,S2); %计算路线长度 df = fS2 - fS1; %计算能力之差 if df < 0 %如果能力降低 接受新路线 S = S2; R = fS2; elseif exp(-df/T)>=rand %以exp(-dC/T)概率接受新路线 S = S2; R = fS2; else %不接受新路线 S = S1; R = fS1; end
5.画路线轨迹图
TSP_Draw_Path.m
function TSP_Draw_Path(Chrom,position_coordinates)
% 画路径函数
%输入
% Chrom 待画路径
% position_coordinates 各城市坐标位置
R = [Chrom(1,:) Chrom(1,1)]; %一个随机解(个体)
figure;
hold on
plot(position_coordinates(:,1),position_coordinates(:,2),'o','color',[0.5,0.5,0.5])
plot(position_coordinates(Chrom(1,1),1),position_coordinates(Chrom(1,1),2),'rv','MarkerSize',20)
for i = 1:size(position_coordinates,1)
text(position_coordinates(i,1)+0.05,position_coordinates(i,2)+0.05,num2str(i),'color',[1,0,0]);
end
A = position_coordinates(R,:);
row = size(A,1);
for i = 2:row
[arrowx,arrowy] = dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2));%坐标转换
annotation('textarrow',arrowx,arrowy,'HeadWidth',8,'color',[0,0,1]);
end
hold off
xlabel('横坐标')
ylabel('纵坐标')
title('轨迹图')
box on6.输出路径函数
TSP_Output_Path.m
function p = TSP_Output_Path(Route) % 输出路径函数 %输入:R 路径 Route = [Route,Route(1)]; N = length(Route); p = num2str(Route(1)); for i=2:N p = [p,'—>',num2str(Route(i))]; end disp(p)
7.可行解路线长度函数
TSP_Feasible_Solution_Path_Length.m
function length = TSP_Feasible_Solution_Path_Length(distance,Chrom) % 计算各个体的路径长度 % 输入: % D 两两城市之间的距离 % Chrom 个体的轨迹 [row,col] = size(distance); NIND = size(Chrom,1); length = zeros(NIND,1); for i=1:NIND p = [Chrom(i,:) Chrom(i,1)]; i1 = p(1:end-1); i2 = p(2:end); length(i,1) = sum(distance((i1-1)*col+i2)); end
8.坐标转换
dsxy2figxy.m
function varargout = dsxy2figxy(varargin)
if length(varargin{1}) == 1 && ishandle(varargin{1}) ...
&& strcmp(get(varargin{1},'type'),'axes')
hAx = varargin{1};
varargin = varargin(2:end);
else
hAx = gca;
end
if length(varargin) == 1
pos = varargin{1};
else
[x,y] = deal(varargin{:});
end
axun = get(hAx,'Units');
set(hAx,'Units','normalized');
axpos = get(hAx,'Position');
axlim = axis(hAx);
axwidth = diff(axlim(1:2));
axheight = diff(axlim(3:4));
if exist('x','var')
varargout{1} = (x - axlim(1)) * axpos(3) / axwidth + axpos(1);
varargout{2} = (y - axlim(3)) * axpos(4) / axheight + axpos(2);
else
pos(1) = (pos(1) - axlim(1)) / axwidth * axpos(3) + axpos(1);
pos(2) = (pos(2) - axlim(3)) / axheight * axpos(4) + axpos(2);
pos(3) = pos(3) * axpos(3) / axwidth;
pos(4) = pos(4) * axpos(4 )/ axheight;
varargout{1} = pos;
end
set(hAx,'Units',axun)9.模拟退火算法主函数
TSP_SA_Main.m
clc;
clear;
close all;
%%
tic
T0 = 1000; % 初始温度
Tend = 1e-3; % 终止温度
L = 200; % 各温度下的迭代次数(链长)
q = 0.9; %降温速率
X=[16.4700 96.1000
16.4700 94.4400
20.0900 92.5400
22.3900 93.3700
25.2300 97.2400
22.0000 96.0500
20.4700 97.0200
17.2000 96.2900
16.3000 97.3800
14.0500 98.1200
16.5300 97.3800
21.5200 95.5900
19.4100 97.1300
20.0900 92.5500];
%%
D = TSP_Distance(X); %计算距离矩阵
N = size(D,1); %城市的个数
%% 初始解
S1 = randperm(N); %随机产生一个初始路线
%% 画出随机解的路径图
TSP_Draw_Path(S1,X)
pause(0.0001)
%% 输出随机解的路径和总距离
disp('初始种群中的一个随机值:')
TSP_Output_Path(S1);
Rlength = TSP_Feasible_Solution_Path_Length(D,S1);
disp(['总距离:',num2str(Rlength)]);
syms x;
%% 计算迭代的次数Time
Time = ceil(double(solve([1000*(0.9)^x==1e-3,num2str(Tend)])));
count = 0; %迭代计数
Obj = zeros(Time,1); %目标值矩阵初始化
track = zeros(Time,N); %每代的最优路线矩阵初始化
%% 迭代
while T0 > Tend
count = count + 1; %更新迭代次数
temp = zeros(L,N+1);
for k = 1:L
%% 产生新解
S2 = TSP_New_Solution(S1);
%% Metropolis法则判断是否接受新解
[S1,R] = TSP_Metropolis(S1,S2,D,T0); %Metropolis 抽样算法
temp(k,:) = [S1 R]; %记录下一路线的及其路程
end
%% 记录每次迭代过程的最优路线
[d0,index] = min(temp(:,end)); %找出当前温度下最优路线
if count == 1 || d0 < Obj(count-1)
Obj(count) = d0; %如果当前温度下最优路程小于上一路程则记录当前路程
else
Obj(count) = Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程
end
track(count,:) = temp(index,1:end-1); %记录当前温度的最优路线
T0 = q*T0; %降温
fprintf(1,'%d\n',count) %输出当前迭代次数
end
%% 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')
%% 最优解的路径图
TSP_Draw_Path(track(end,:),X)
%% 输出最优解的路线和总距离
disp('最优解:')
S = track(end,:);
p = TSP_Output_Path(S);
disp(['总距离:',num2str(TSP_Feasible_Solution_Path_Length(D,S))]);
disp('-------------------------------------------------------------')
toc命令行窗口
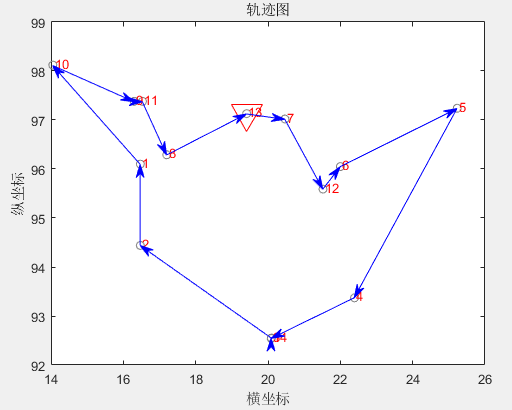
初始种群中的一个随机值: 7—>4—>8—>2—>6—>11—>10—>14—>13—>9—>3—>12—>1—>5—>7 总距离:70.2021 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 最优解: 13—>7—>12—>6—>5—>4—>3—>14—>2—>1—>10—>9—>11—>8—>13 总距离:29.3405 ------------------------------------------------------------- 时间已过 2.769450 秒。
随机路线图
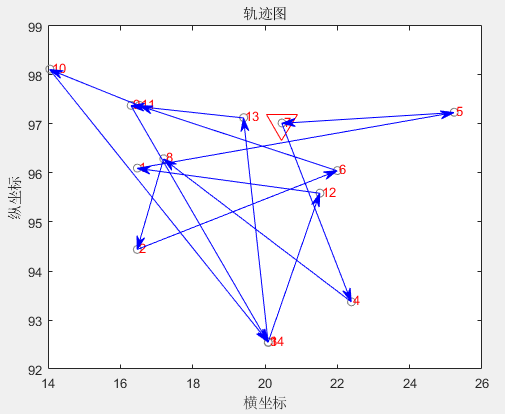
进化过程
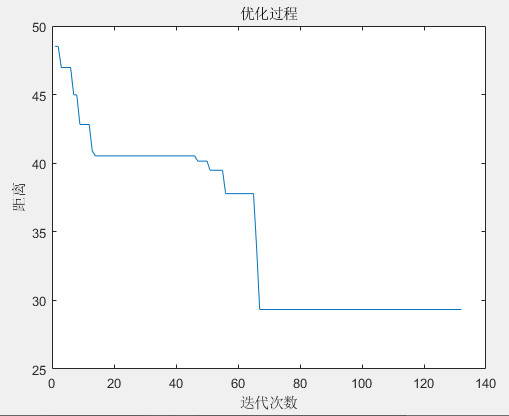
最优解路线图
================================================
一,算法简介
1.1 内容简介
对于某个问题而言,没有很好的办法可以直接求得它的最优解,又或是直接求解太复杂。此时,我们尝试随机带入一些值,想要试一下,撞一下大运,看看能不能撞出比较好的解出来。
1.2 算法实现的过程
第一步,我们将根据可控变量的取值范围,来随机选取初始值,这是初次试值
第二步,接下来的试值中,我们会给每一个变量,产生一个微小的变化量delta= (delta具体是多少,可以由用户决定。
代表变化后的可控变量,
代表变化前的可控变量),当然变化后的每一个变量要求在取值范围以内。注意,这个微小变化量是随机取值的,但是要保证它的取值范围关于原点对称。
注意,可控变量可能不是一维的,可能是二维或者更高维度。此时 为一个存储多个可控变量的向量。
第三步,我们自定义了的函数关系,这个函数是针对当前问题的,是变量到结果的映射。这个函数的输入端是向量 ,输出端是映射后的结果
。假设
映射后的结果是
;
映射后的结果是
对于 我们提出如下要求:
1)如果新的结果更接近我们想要的结果(一般我们想要找到的是最值),我们就直接接受当前得到的 及
。
2)如果新的结果 远离或者等于原来的结果,我们以一定概率 P 的去接受当前状态下的变量。假设 函数值的变化量
,温度为 T (这是用户自己设置的一个量,用于调控算法在起始及过程当中的概率大小)。则 P 满足如下关系:
并且,我们要求,如果你是以概率的方式接受了当前状态下的结果,那么在每次接受以后,温度将会下降,即 =
*
。注意,T 的初始值是人为设定的,
也是人为设定的。
3)当 P 过于小的时候,或长时间找不到更优的解,那么结束算法。
1.3 重点讲解
1)不难发现,对于 P 而言,由于指数的分子恒为正,当指数分母趋于无穷大的时候,概率趋于1。这意味我们选择远离或者等于原来的结果的可能性会比较高。刚开始的时候,我们需要接触更多的区域,来试探解的结果,所以温度会设定的很高。随着算法的进行,温度逐渐降下来后,P 会逐渐变小。最后,我们能够得到一个尽可能接近最优解的解。
2)如何实现求解最大值呢?首先,使得 ,那么由于我们要求
,所以当
,此时的
是我们不想要的解,也就是我们想要更大的解。其次,写下一个判断函数 judge(dE,t),传入
和 t ,其中,dE =
。当dE < 0 时,返回值1,代表接受结果;当dE ≥ 0 时,进行概率选择,依照概率返回值 1 或 0 。
该算法计算的就是最大值。如果我们使得 ,就可以通过输入的extreme值来修改计算的最值了,当 extreme=1 时,计算最大值;当 extreme=-1 时,计算最小值。(注意,下面编程当中的
,所以和这里刚好相反。)
二,算法的matlab编程
首先考虑一下算法的整体结构:输入端,循环处理的过程,输出端
输入端:
包括温度 T 、温度最小值 Tm 、温度下降系数 alpha 、变量矩阵 X 及其取值范围、自定义的函数 val()
变量矩阵 X 用于存储已知条件,它是一个 m*n 的矩阵,其中 m 代表已知点的个数,而 n 代表每个点的维度。
循环处理过程:
包括这几个部分,初始图像的绘制、初始值的求解、随机扰动的求解、是否采纳解的判断、绘图。
输出端:
主要需要最终的温度T,和最后得到的状态下的变量及其函数值
matlab编程
(原代码来源于https://zhuanlan.zhihu.com/p/33184423中的第二例,但是我将算法改进了一下,目的是使其更具有普遍性)
使用模拟退火算法求解到点集直线距离之和最短的点
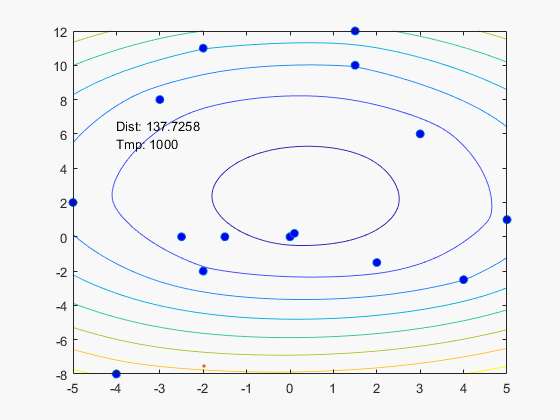
%{
名称:模拟退火算法
用途:用于求某个函数的最值
输入:温度、温度最小值、温度下降系数、变量矩阵及其取值范围、自定义的函数val
输出:函数图像,以及最终得到的值y
注意:
%}
clc, clear
%用户输入参数
disp('请修改关于变量矩阵的自定义函数,初始及初始图像函数,还有循环过程中的绘图部分');
T_input=input('请以向量的形式依次输入tmp,tmp_min,alpha:');
tmp=T_input(1);tmp_min=T_input(2);alpha=T_input(3);
varied_data=input('请输入变量矩阵,每一列代表不同维度,每一行代表不同元素:');
extreme=input('需要计算最大值请输入-1,计算最小值请输入1:')
%实验参数,可以将上面内容注释掉,把这里取消注释进行实验
%tmp = 1000;
%tmp_min = 0.001;
%alpha = 0.98;
%extreme=-1;
%varied_data=[0 0;1.5 10;1.5 12; -2 11; -4 -8;-5 2;2 -1.5;4 -2.5;5 1;-2 -2;-3 8;3 6;-1.5 0;-2.5 0;0.1 0.2];
draw_dist(varied_data);
[varied_data_new,tmp,counter]=tuihuo(tmp,tmp_min,alpha,varied_data,extreme);
%%
%此为自定义函数,不同题目需要有不同的自定义函数,用户需要自行修改
function [result] = val(varied_data,varied_single_data)
x=varied_data(:,1);
y=varied_data(:,2);
xx=varied_single_data(1);
yy=varied_single_data(2);
result = 0;
num_of_dots = length(x);
for i = 1:num_of_dots
result = result + sqrt((xx - x(i))^2 + (yy - y(i))^2);
end
end
%%
%此为绘制初始图像的函数,针对不同的情况,用户需要自行更改
function []=draw_dist(varied_data)
x=varied_data(:,1);
y=varied_data(:,2);
x_min = floor(min(x));
y_min = floor(min(y));
x_max = ceil(max(x));
y_max = ceil(max(y));
resol = 10;
dx = x_min: 1/resol : x_max;
dy = y_min: 1/resol : y_max;
[xx, yy] = meshgrid(dx, dy);
zz = zeros(length(dy), length(dx));
for ii = 1:length(dx)
for jj = 1:length(dy)
zz(jj, ii) = val(varied_data,[dx(ii), dy(jj)]);
end
end
contour(xx, yy, zz);
hold on;
scatter(x, y, 'MarkerFaceColor','blue');hold on;
end
%%
%退火的主体函数
function [varied_data_new,tmp,counter]=tuihuo(tmp,tmp_min,alpha,varied_data,extreme)
%判断变量维度及个数
[m,n]=size(varied_data);
%自动生成初始值并判断
for i=1:1:n
varied_data_max(i)=max(varied_data(:,i));
varied_data_min(i)=min(varied_data(:,i));
varied_data_old(i) = (varied_data_max(i)-varied_data_min(i))*rand()+min(varied_data(:,i));%生成初始值
end
s_old = val(varied_data,varied_data_old);
s_new = s_old;
text_lt = text(0, 0, 'Init');
%计数器
counter = 0;
%退火的主体部分,一个循环
while(tmp > tmp_min)
%随机扰动,需要保证扰动后的变量处于定义域内
varied_new_mark=1;
while(sum(varied_new_mark))
for i=1:1:n
delta(i) = rand() - 0.5;%此处可以自行更改大小
varied_data_new(i)=varied_data_old(i) + delta(i);
if(varied_data_new(i)<varied_data_min(i) || varied_data_new(i)>varied_data_max(i))
varied_new_mark(i) = 1;%变量不能超出上下限
break
else
varied_new_mark(i) = 0;
end
end
end
s_new = val(varied_data,varied_data_new);
%求差值,extreme=1时,求最小值;=-1时,求最大值
dE = (s_new - s_old)*extreme;
%判断
j = judge(dE, tmp);
if(j)
s_old = s_new;
varied_data_old = varied_data_new;
end
%只有当dE < 0的情况下才降温
if(dE < 0)
%这里时循环过程中的绘图部分,请依照具体情况修改
delete(text_lt);
text_lt = text(-4, 6, {['Dist: ',num2str(s_old)];['Tmp: ', num2str(tmp)]});
scatter(varied_data_old(1), varied_data_old(2), '.');%这里可以修改字符出现的位置
pause(0.001);
tmp = tmp * alpha;
else
counter = counter + 1;
end
%当接受更差的解的概率太小时,若又长时间找不到更优的解,那么退出循环,结束算法
if(counter > 10000)%这里可以修改计数器的最大值
break;
end
end
end
%%
%{
名称:judge
用途:用于在随机扰动以后,判断是否选择这组数据
输入:扰动前后的变化量dE,退火温度t
输出:状态y,若y=1,为选择;y=0,为不选择
注意:
%}
function [y] = judge(dE, t)
if(dE < 0)
y = 1;
else
d = exp(-(dE / t));
if(d > rand)
y = 1;
else
y = 0;
end
end
end
========================================
模拟退火算法简介

下面以一个实例来讲解模拟退火算法求解TSP问题
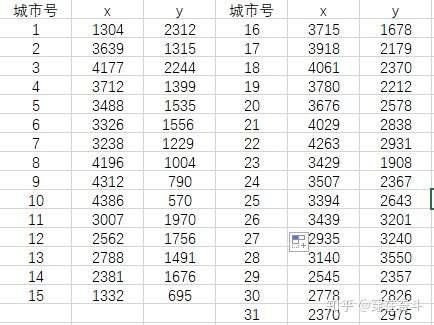
第一步就是加载城市坐标,然后处理
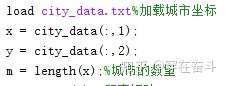
第二步计算各个城市之间的距离,并创建距离矩阵,我采用的各个城市之间距离的计算公式为
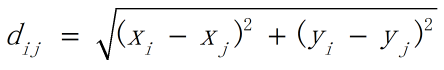
距离矩阵是一个对称矩阵,对称线上为0

第三步就是随机生成一条线路,取得路线的路径相对较小的一条线路

最后一步就是模拟退火过程
降温系数设置为at=0.999,即new——T=at X old——T,终止温度选为e=10E-30,T设置为1。
在相对路径距离较小的基础上随机选择两个城市号进行交换,组成新的路径
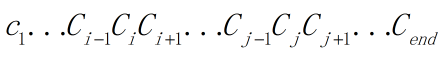
交换i和j两个城市的位置,同时i和j中间的城市倒换顺序交换后的路径为
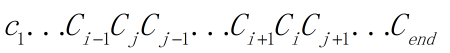
得到两条路径的距离差为
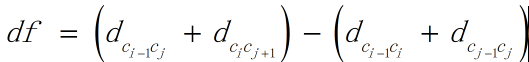
接受准则就是

即当df<0时,也就是新路径距离比老路径距离小,否则就是依概率接受新路径。

然后就是降温了,也就是判断是否满足迭代条件,如果满足就停止迭代了
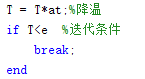
最后的运行结果就是
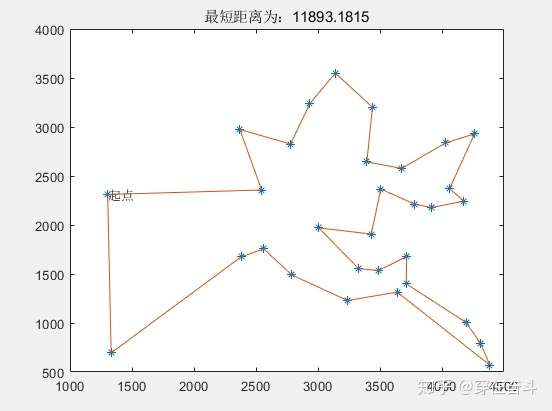
最后附上完整代码
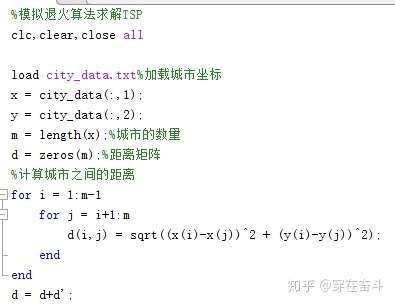




参考:https://zhuanlan.zhihu.com/p/585495727


