MTALAB——BP网络
参考地址:https://blog.csdn.net/wzxq123/article/details/65635809
https://blog.csdn.net/raiden_chen_42/article/details/78087277
https://blog.csdn.net/caokaifa/article/details/81163973
https://blog.csdn.net/low5252/article/details/103358352
深度学习:
https://www.bilibili.com/video/BV1sK4y157w7?p=3&spm_id_from=pageDriver
1、feedforwardnet函数
feedforwardnet是matlab最新的用语创建前向BP网络的函数。
使用示范1:
[x,t] = simplefit_dataset; % MATLAB自带数据
net = feedforwardnet; % 创建前向网络
view(net)
net = train(net,x,t); % 训练,确定输入输出向量的维度
view(net) % 查看网络的可视化图
y = net(x); % 计算预测值
perf = perform(net,y,t) % 计算误差性能
feedforwardnet ():
综述:包含一系列的层次。第一层与网络输入连接。接下来的层次与上一次连接。最后一层产生网络的输出。feedforward网络可以用作输入和输出的映射,只含有一个隐含层的的神经网络可以拟合任意有限的输入输出映射问题。输入的变量有两个可以选择

%---------------------------------------------------
% 指定训练函数
%---------------------------------------------------
% net.trainFcn = 'traingd'; % 梯度下降算法
% net.trainFcn = 'traingdm'; % 动量梯度下降算法
%
% net.trainFcn = 'traingda'; % 变学习率梯度下降算法
% net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法
%
% (大型网络的首选算法)
% net.trainFcn = 'trainrp'; % RPROP(弹性BP)算法,内存需求最小
%
% (共轭梯度算法)
% net.trainFcn = 'traincgf'; % Fletcher-Reeves修正算法
% net.trainFcn = 'traincgp'; % Polak-Ribiere修正算法,内存需求比Fletcher-Reeves修正算法略大
% net.trainFcn = 'traincgb'; % Powell-Beal复位算法,内存需求比Polak-Ribiere修正算法略大
%
% (大型网络的首选算法)
%net.trainFcn = 'trainscg'; % Scaled ConjugateGradient算法,内存需求与Fletcher-Reeves修正算法相同,计算量比上面三种算法都小很多
% net.trainFcn = 'trainbfg'; % Quasi-NewtonAlgorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快
% net.trainFcn = 'trainoss'; % One Step SecantAlgorithm,计算量和内存需求均比BFGS算法小,比共轭梯度算法略大
%
% (中型网络的首选算法)
%net.trainFcn = 'trainlm'; % Levenberg-Marquardt算法,内存需求最大,收敛速度最快
% net.trainFcn = 'trainbr'; % 贝叶斯正则化算法
%
% 有代表性的五种算法为:'traingdx','trainrp','trainscg','trainoss','trainlm'
默认情况下神经网络参数:
层数:1、输出输入:1、
重点是怎么设置各个参数:
参数的设置和newff的一样,应该是所有网络都可以这样设置。
示范2:
%% feedforwardnet函数用法
%拟合sin(k*x)函数,,目的:比较不同隐含层神经元个数的拟合效果
figure
i = 1;
x = -2:.1:2;
hiddenSizes = [1; 5; 10; 30; 50; 80]; %隐层个数,分别取1、5、10、30、50和80
perf = zeros(size(hiddenSizes, 1),5); %保存拟合的误差值
for hs = 1:size(hiddenSizes, 1) %size(A,1)取矩阵的行数
net = feedforwardnet( hiddenSizes(hs) ); %bp神经网络
for k = 1:5
t = cos(k * x);
net = train(net, x, t);
y = net(x);
perf(hs, k) = perform(net, y, t);
fprintf("hs = %d k = %d : \n\tperf=%e\n\n", hs, k, perf(hs, k))
subplot(size(hiddenSizes, 1),5,i);
i = i + 1;
plot(x, t, 'r.',x, y,'g-');
ax = gca; ax.YLim = [-1 1]; ax.XTick = []; ax.YTick = [];
end
end
在命令行窗口运行以上代码,开始训练Bp网络:
拟合结果:
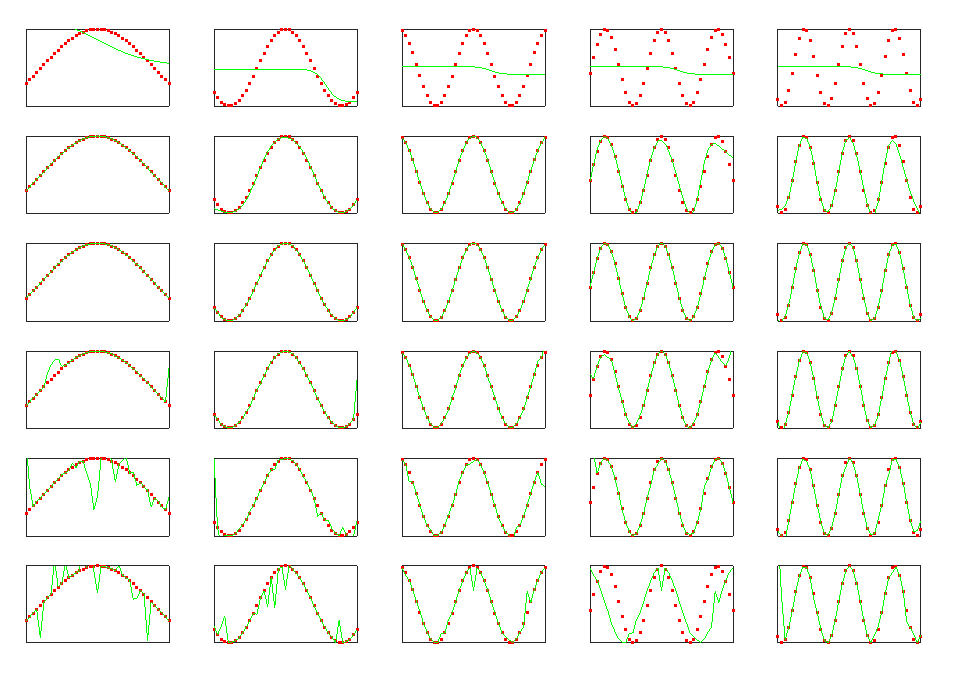
由结果可见:
①k一定,隐含层神经元个数越大,拟合效果越好,超过一定的程度,影响效果不显著甚至出现过拟合;
②k比较大时,隐含层神经元个数如果太小会导致拟合不足;
③k比较小时,隐含层神经元个数如果太大会导致拟合过度;
④拟合效果一致时,所需的隐含层神经元个数随着k的增大而增大。


