1. 牛顿法求解方程的根

有时候，在方程比较复杂的情况下，使用一般方法求解它的根并不容易。牛顿法通过迭代的方式和不断逼近的思想，可以近似求得方程较为准确的根。

牛顿法求根的核心思想是泰勒一阶展开。例如对于方程 f(x) = 0，我们在任意一点 x0 处，进行一阶泰勒展开：

令 f(x) = 0，带入上式，即可得到：

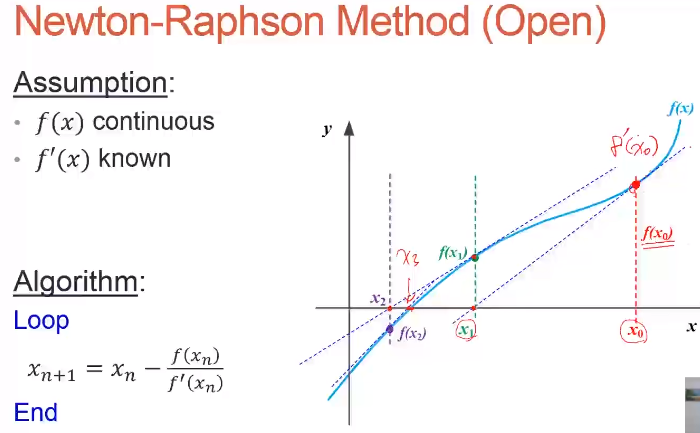
注意，这里使用了近似，得到的 x 并不是方程的根，只是近似解。但是，x 比 x0 更接近于方程的根。效果如下图所示：

然后，利用迭代方法求解，以 x 为 x0，求解下一个距离方程的根更近的位置。迭代公式可以写成：

经过一定次数的有效迭代后，一般都能保证在方程的根处收敛。下面给出整个迭代收敛过程的动态演示。

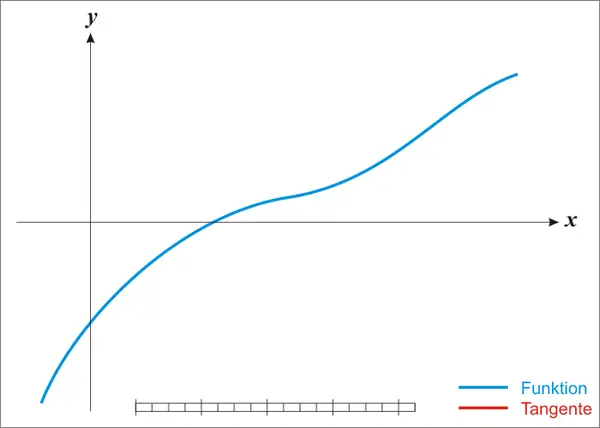
2. 牛顿法凸优化

上一部分介绍牛顿法如何求解方程的根，这一特性可以应用在凸函数的优化问题上。

机器学习、深度学习中，损失函数的优化问题一般是基于一阶导数梯度下降的。现在，从另一个角度来看，想要让损失函数最小化，这其实是一个最值问题，对应函数的一阶导数 f'(x) = 0。也就是说，如果我们找到了能让 f'(x) = 0 的点 x，损失函数取得最小值，也就实现了模型优化目标。

现在的目标是计算 f’(x) = 0 对应的 x，即 f’(x) = 0 的根。转化为求根问题，就可以利用上一节的牛顿法了。

与上一节有所不同，首先，对 f(x) 在 x0 处进行二阶泰勒展开：

对上式左右两边求导，然后令 f’(x) = 0 ，可得：

同样，虽然 x 并不是最优解点，但是 x 比 x0 更接近 f'(x) = 0 的根。这样，就能得到最优化的迭代公式：

通过迭代公式，就能不断地找到 f'(x) = 0 的近似根，从而也就实现了损失函数最小化的优化目标。

实验要求：用牛顿法求方程 sin(x*2)- exp(x/5)+1.2=0，在【1-2】之间的根。

clc

f=@(x)sin(x*2)- exp(x/5)+1.2;

fd=@(x)2*cos(2*x) - exp(x/5)/5;

x=1  ;

for n=1:10

  

       x=x-f(x)/fd(x);

       vpa(x)    

       pause()

end

 vpa(x)    

fzero函数解方程的过程：