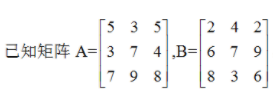数组与矩阵常用函数
MATLAB中的特殊矩阵与数组 在本节中,我们将讨论学习一些创建一些特殊数组的函数。对于这些函数,单个参数创建一个正方形数组,双参数创建矩形数组。
[ ]
生成空矩阵
eye(n,m)
生成n×m单位矩阵
ones(n,m)
生成全部元素是1的矩阵
zeros(n,m)
生成全部元素是0的矩阵
magic(n)
生成魔方矩阵
rand(n,m)
生成0~1之间均匀分布的随机矩阵
randi([min,max],n,m) 生成 [min,max] 范围内 n 行 m 列的随机整数矩阵 randn(n,m) 生成均值为0,方差为1的标准正态分布的随机矩阵 randperm(n)
返回一行包含从 1 到 n 的整数的乱序(洗牌算法)
(1)zeros( )函数 是用来创建一个全零的数组 -例如 :
>> zeros(5) %生成5行5列的全0矩阵
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
(2)ones( )函数 创建一个所有元素为1的数组 -例如
>> ones(4,3)
ans =
1 1 1
1 1 1
1 1 1
1 1 1
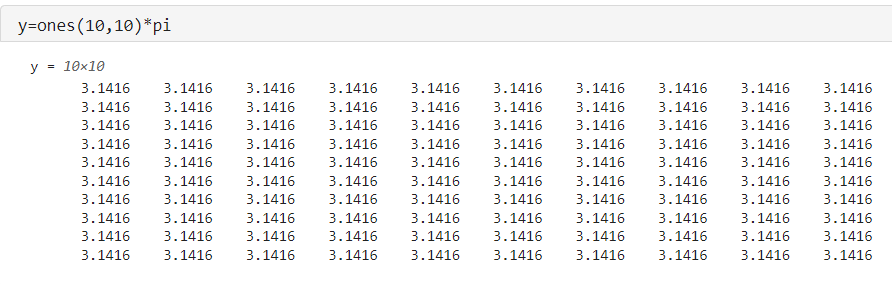
如果需要一个大小为10*10,且全部元素都是圆周率pi的矩阵,可以采用:
(3)eye( )函数 创建一个单位矩阵。例如
>> eye(4)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
(4)魔方 magic( )函数
magic( )函数创建一个魔术方阵。这需要一个参数,指定正方形的大小。 参数必须是大于或等于3的标量。
>> magic(3)
ans =
8 1 6
3 5 7
4 9 2
>> magic(4)
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
(5)rand( )函数
rand( )函数在(0,1)上创建均匀
调用格式: rand(n,m), 这里 n,m 是生成 n 行 m 列处于 0~1 之间的随机数
>> rand(3, 5) 我们当然可以根据自己需要生成任何范围内的随机数: 比如想生成处于 0-2pi 的随机数,只需要将上面的式子改为 a=2*pi*rand(2,3)
生成结果:
练习1:模拟生成全班50个同学的期末成绩,要求所有人成绩都在60-100之间随机分布。
(6)随机整数: randi函数
格式: randi ([min,max],n,m );生成 [min,max] 范围内 n 行 m 列的随机整数矩阵
例子: randi( [-2 , 10] , 2 , 3 )
得到:
也可以写成: randi ( max , n , m); 生成 1-max 范围内 n 行 m 列的随机整数矩阵
>> randi( 20, 2 , 3 )
ans =
17 13 17
16 8 11
练习2:模拟生成全班50个同学的期末成绩,要求所有人成绩都在60-100之间随机分布,且成绩为整数。
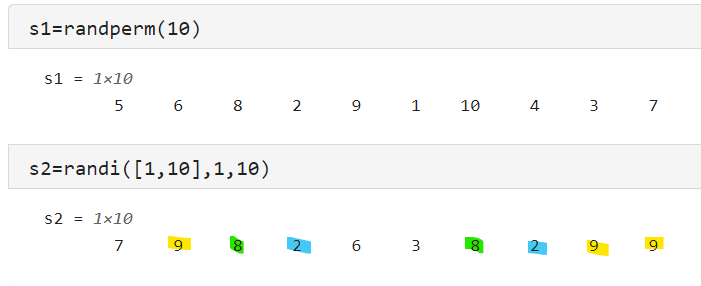
(7) randperm()函数用法返回一行包含从1到n的乱序的整数序列。
语法: p = randperm(n) ; 返回一行包含从 1 到 n 的乱序的整数序列。
相当于对1- n之间的整数进行‘ 洗牌 ’处理!
>> x=randperm(10)
x =
4 8 3 1 2 7 6 10 9 5
p = randperm(n,k) 返回一行从 1 到 n 的整数中的 k 个,且这 k 个数是不重复的。
>> x=randperm(10,5)
x =
7 1 2 3 4
randperm 是不重复的重排采样( k-permutations ), randi( [min,max] ,n,m )则允许重复采样 。
(8)正态分布的随机数: randn函数
randn函数可以用于生成符合正态分布的随机数
格式: randn(n,m);生成 n 行, m 列,以 0 为中心的正态分布随机数
>> s=randn(3,4)
s =
-1.7947 0.1001 -0.6003 1.7119
0.8404 -0.5445 0.4900 -0.1941
-0.8880 0.3035 0.7394 -2.1384
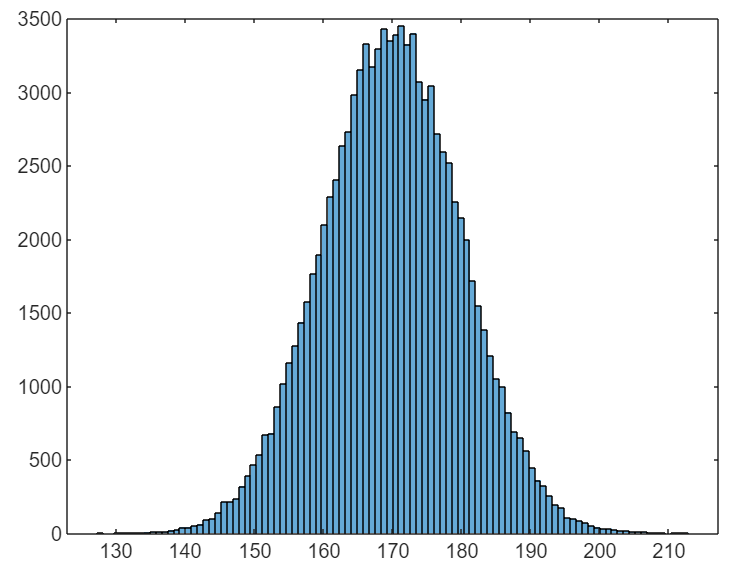
再看一个例子,模拟中国男性的身高分布 :
y=randn(1,100000)*10+170 % 生成以 170 为中心,方差为10的100000个正态分布的随机数
histogram(y,100) % 画出这100000个数据的直方图
tips:直方图的纵轴代表每个区间元素的数目。
如果要获得一个服从正态分布N(u,o*o)的随机数,可执行 randn(n)*o+u
练习3:模拟生成50个同学的毕业后的月收入,以5000为正太分布中心,方差为800。
2.多维数组(矩阵) 具有二维以上的数组在MATLAB中被称为多维数组。MATLAB中的多维数组是正常二维矩阵的扩展。
可以用如下方式生成 3×3 ×2数组 :
a(:, :, 1) = [ 7 9 5; 6 1 9; 4 3 2]; >> size(a) a(:,:,1) =
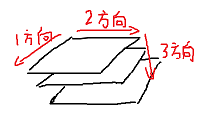
如何理解多维数组?
比如,某个三维数组结构为 4×5 ×6 ,那么可以 想象成一张纸(上面写了4行5列的数字,构成一个4×5的平面矩阵 行5列的数字
思考: 4×5 ×6 ×3的多维数组该怎么理解?
还可以使用 o nes( ) , zeros( ) 或 rand( ) 函数来创建多维数组。
例如:
>> b1 = rand(4,3,2) %创建3维随机数组 b1(:,:,1) = >> b2 = rand(4,5,3,2) %创建4维随机数组 b2(:,:,1,1) =
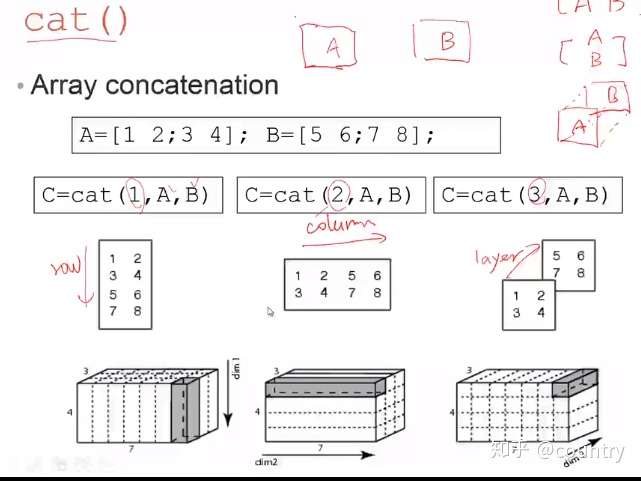
也可以使用 cat( ) 函数来构建多维数组。 它沿着指定的维度连接数组列表.
cat()函数的语法是 :B=cat(dim,A1,A2...)
% 其中: B是创建的新阵列;
% A1,A2,...是即将要拼接的数组;
% dim是连接数组的维度方向,dim=1为平面上的竖直方向,dim=2为平面上的水平方向,dim=3为从第上层平面指向最底层平面的方向
例1:
clc
a = [ 1,2,3 ; 4,5,6 ; 7,8,9 ];
b = [ 1 0 1 ; 2 0 2 ; 3 0 3 ]
c1 = cat(1 ,a,b) % 表示把a,b矩阵纵向 拼接
c2 = cat(2 ,a,b) % 表示把a,b 矩阵水平 拼接
c3 = cat(3 ,a,b) % 表示把a,b 矩阵沿Z轴 方向拼接
例2:
x1 = [9 8 7; 6 5 4; 3 2 1]; y=cat(3,x1,x2,x3,x4); %把x1,x2 , x3, x4 这4个平面矩阵按z轴方向拼接成一本“书”。 %把第2面的数据全部索引出来 y(1,3,:) %把所有面的第1行第3列的数据全部索引出来 执行上面示例代码,得到以下结果 -
y(:,:,1) =
计算机存储图片的原理:
黑白模式 (单色图像、二值图像):像素只有黑白以及中间的过渡灰色。
图片由黑色区域和白色区域组成。每个像素的值在0-1之间 或0-255之间 不同 体系);
如,0-1体系
按照0-255体系,则有:
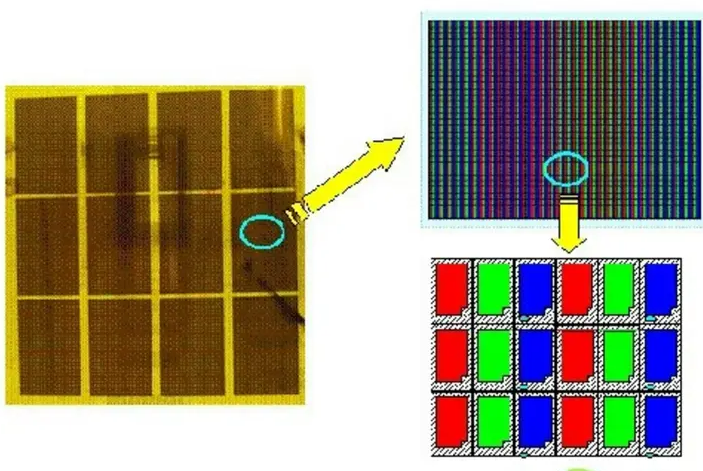
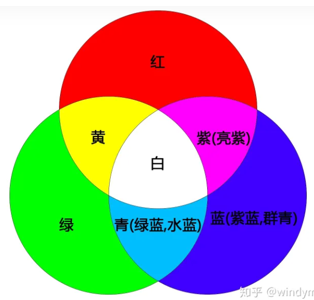
RGB彩色模式: RGB三盏灯的亮度就可以组合出该像素点的颜色和亮度!
LED显示器的一个像素的结构:
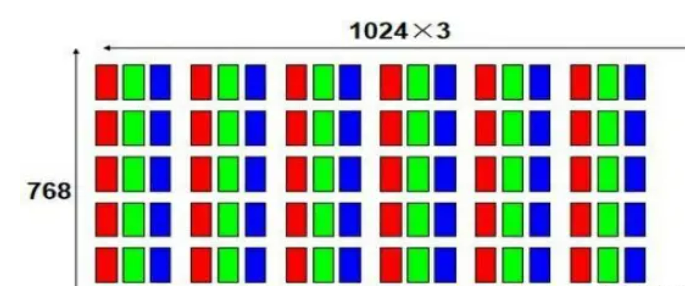
显示屏就是由很多个像素点组成的像素阵列,如经典的1024*768显示屏:
为什么三原色是红绿蓝而不是紫色、粉色、或者橙色呢?是因为人类的视网膜上面的 视锥细胞 对红绿蓝三色最敏感!
总结:
(1)每一个像素由RGB三个分量组成。注意, RGB三个分量值相同时为灰色(或黑白色)。
(2)一副彩色数字 图像由R, G, B三个通道构成,可以看做一个三维数组。
(2)每个分量各占8位,其范围为0~255,每个像素24位比特(8*3bit,3字节)。
关于显卡,这里直接引用下百度百科:
显卡全称显示接口卡,又称显示适配器,是计算机最基本配置、最重要的配件之一。显卡作为电脑主机里的一个重要组成部分,是电脑进行数模信号转换的设备,承担输出显示图形的任务。显卡接在电脑主板上,它将电脑的数字信号转换成模拟信号让显示器显示出来,同时显卡还是有图像处理能力,可协助CPU工作,提高整体的运行速度。
数据从离开CPU到达显示屏,中间必须通过如下4个步骤:
1.从总线进入GPU(图形处理器):将CPU送来的数据送到北桥,再送到GPU里面进行处理。
2.将芯片处理完的数据送到显存。
3.从显存读取出数据再送到随机读写存储数—模转换器进行数模转换的工作。(但是如果是DVI接口类型的显卡,则不需要经过数字信号转模拟信号。而直接输出数字信号。)
4.从DAC进入显示器:将转换完的模拟信号送到显示屏。
显卡就是起数据处理和数模转换的作用,像数模转换、模数转换这些都是数字信号处理、数字电路之类的学科的知识了~
以上便是CPU到显卡再到显示器再到人眼的过程。
练习:设计一个3*3*3的3维数组pic ,通过imshow( )函数显示pic, 在屏幕上得到一个3行3列(一共9个像素点)的小图片,这个图片上的颜色分布为:
clc
r=[ 0 1 0.5
1 0 0
1 0 1 ]
g=[ 0 1 0.5
0 1 0
1 1 0 ]
b=[ 0 1 0.5
0 0 1
0 1 1 ]
pic=cat(3,r,g,b)
imshow(pic)
%在计算机系统内,RGB颜色更 0-255 uint8 类型 )。 此颜色系统可以描述16581375种颜色!
中国传统颜色之美 https://www.bilibili.com/video/BV1zv411K7Bt
http://zhongguose.com/
https://colors.ichuantong.cn/
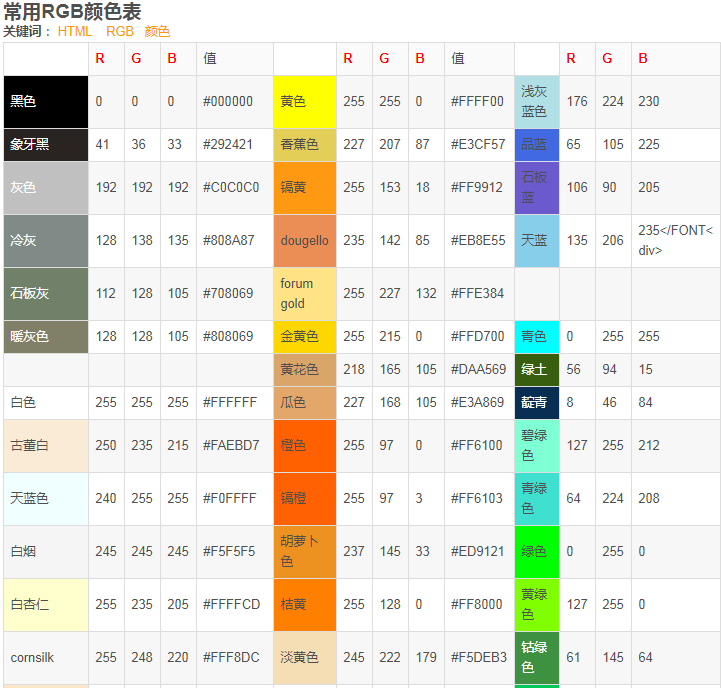
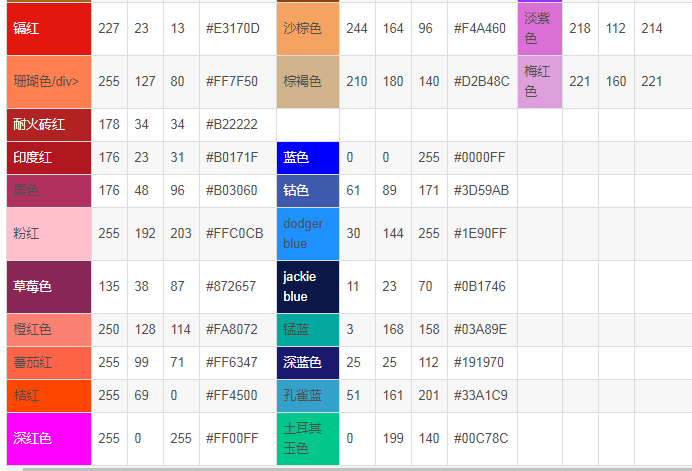
颜色表:
①红色系00:06 ,F47983桃红00:08 ,9D2933胭脂红00:11 00:14 ,ED5736妃色00:18 ,FF2121大红00:21 00:24 ,EF7A82嫣红00:28 ,ED556A山茶红00:30 00:33 ,F1939C春梅红00:37 ,DE2A18夕阳红00:40 00:43 ,FF461F朱砂00:46 ,FF461F檀00:49 00:52 ,D11A2D枫叶红00:56 ,ED3321樱桃红00:59 01:02 ,C82111F殷红01:05 ,F03752海棠红01:08 01:12 ,A7535A满江红01:15 ,FF2D51火红01:18 01:21 ,894E54烟红01:24 ,C04851玉红01:27 01:30 ,A6522C绀红01:34 ,8C4356绛紫01:37 01:40 ,A98175绾01:43 ,ED5A65艳红01:46 01:49 ,EE3F4D茶花红01:53 ,C3272B赤01:56 01:59 ,F9906F酡颜02:03 ,F05654银红02:06 02:08 ,EF3473品红02:12 ,FF4E20丹02:15 02:19 ,FFFBF0象牙白02:22 ,E0F0E9素02:25 02:28 ,F0F0F4铅白02:32 ,F2ECDE缟02:35 02:38 ,D1D9E0苍白02:41 ,F3F9F1荼白02:44 02:48 ,EEDEB0牙色02:51 ,E9E7EF银白02:54 02:57 ,E9F1F6霜色03:00 ,FEEFE8鱼肚白03:04
③黄色系
FFC773姜黄03:08 ,C89B40昏黄03:10 ,FF8C31杏红03:13 03:16 ,D3BE7D枯黄03:19 ,C9DD22柳黄03:22 03:25 ,FF7500橘红03:28 ,FF8936橘黄03:31 03:34 ,FFA400橙黄03:37 ,CA6924琥珀03:40 03:43 ,D9B611秋香色03:46 ,F0C239缃色03:49 03:52 ,B35C44茶色03:55 ,FAFF72鸭黄03:58 04:01
04:06 ,9ECCAB明绿04:08 ,BACF65果绿04:12 04:14 ,8CC269水绿04:18 ,61AC85淡绿04:20 04:23 ,BDDD22嫩绿04:27 ,20A162翠绿04:29 04:32 ,A4E2C6艾绿04:35 ,B7D07A芦苇绿04:38 04:41 ,AFDD22柳绿04:45 ,43B244鲜绿04:47
⑤青色系
2EDFA3玉色04:51 ,7BCFA6石青04:54 ,1BD1A5碧色04:57 05:00 ,C0BD7青白05:03 ,00E079青翠05:06 05:10 ,424C50雅青05:12 ,E0EEE8鸭卵青05:15
05:20 ,baccd9云水蓝05:22 ,2b73af品蓝05:25 05:28 ,4b5cc4宝蓝05:31 ,93b5ef星蓝05:34 05:37 ,c6e6e8海天蓝05:40 ,66a9c9涧石蓝05:43 05:46 ,134857苍蓝05:49 ,29b7cb蔚蓝05:52 05:55 ,2177b8虹蓝05:58 ,d0dfe6远天蓝06:01 06:04 ,425066黛蓝06:07
06:12 ,1e131d乌梅紫06:14 ,310f1b墨紫06:17 06:20 ,5c2223暗玉紫06:23 ,2b1216李紫06:26 06:29 ,c06f98樱草紫06:32 ,801dae青莲06:35 06:38 ,56004f紫棠06:41 ,9b1e64苋菜紫06:44 06:47 ,8076a3藤萝紫06:50 ,ad6598豆蔻紫06:53 06:56 ,b0a4e3雪青06:59 ,574266黛紫07:02 07:05 ,681752牵牛紫07:02
07:13 ,392f41乌黑07:15 ,758a99墨灰07:18 07:21 ,161823漆黑07:24 ,808080灰07:27 07:30 ,3d3b4f玄青07:34 ,493131缁色07:36 07:39 ,75664d黎07:42 ,000000黑07:45 07:48 ,6b6882黝(音同友)07:51 ,5d513c黧(音同黎)07:54 07:57
08:02 ,f2be45赤金08:04 ,eacd76金色08:07
多维数组的应用实例:三维数组作为图片。
imshow(pic)函数: imshow(pic)可以把三维数组pic作为一个图片来显示。
在使用 imshow(pic)函数 的时候: 如果矩阵 pic的数据类型为double类型,则pic的数据的值应该是0-1范围;如果pic为uint8 类型,则pic的 数据的值 应该是0-255范围!
例:灰度图( 即,对任何一个像素点,其rgb三个通道的值是相同的 )
k=0.65 ; %参数k控制灰度
pic_gray= ones (100,100,3 )* k ;
%或者 ones(100,100)* k也可以,此时imshow()自动把RGB三个通道都用该二维矩阵来显示。
imshow( pic_gray ) %把2维数组当成黑白图片来显示。
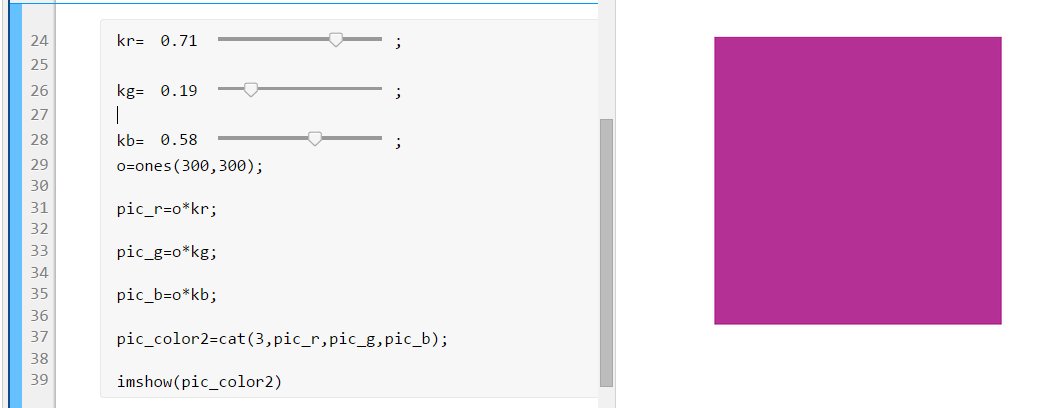
例:RGB三通道的值对颜色的控制
kr= 0.631;
kg= 0.213;
kb= 0.323;
o=ones(300,300);
pic_r= o*kr;
pic_g=o*kg;
pic_b=o*kb;
pic_color2=cat(3,pic_r,pic_g,pic_b);
imshow(pic_color2)
还可以使用实时编辑器,采用数值滑块,动态调整颜色。
例:随机函数生产图片
pic_gray1=rand(100,100);
imshow ( pic_gray1 ) %把2维数组当成黑白图片来显示。
pic_color2=rand(100,100,3);
imshow( pic_color2 ) %把三维数组当成三通道彩色图片来显示。
0-1模式(double类型)图像显示:
%比如需要柿子色
kr=237;
kg=110;
kb=69;
o=ones(300,300);
pic_r=o*kr/255;
pic_g=o*kg /255;
pic_b=o*kb /255;
pic_color2=cat
imshow(pic_color2)
0-255模式(uint8
如果采用0-255模式来显示图像,则数据类型对应为uint8
kr=238;
kg=39;
kb=70;
o=ones(300,300);
pic_r= o*kr;
pic_g=o*kg;
pic_b=o*kb;
pic_color1=cat(3,pic_r,pic_g,pic_b); %把r,g,b三个二维数组拼接成三维数组
pic_color2=uint8 (pic_color1); %转换为uint8类型
imshow(pic_color2)
试一下显示如下的蓝色:
0-255模式( uint8 类型)图像显示:
如,显示 ' F03752 海棠红',首先要把海棠红的16进制的颜色代码转换为十进制。
kr=hex2dec('F0');
kg=hex2dec('37');
kb=hex2dec('52');
o=ones(500,500);
pic_r=o*kr;
pic_g=o*kg;
pic_b=o*kb;
pic_color1 =cat(3,pic_r,pic_g,pic_b);
pic_color2 =uint8 (pic_color1 ); %转换为uint8类型
imshow(pic_color2 )
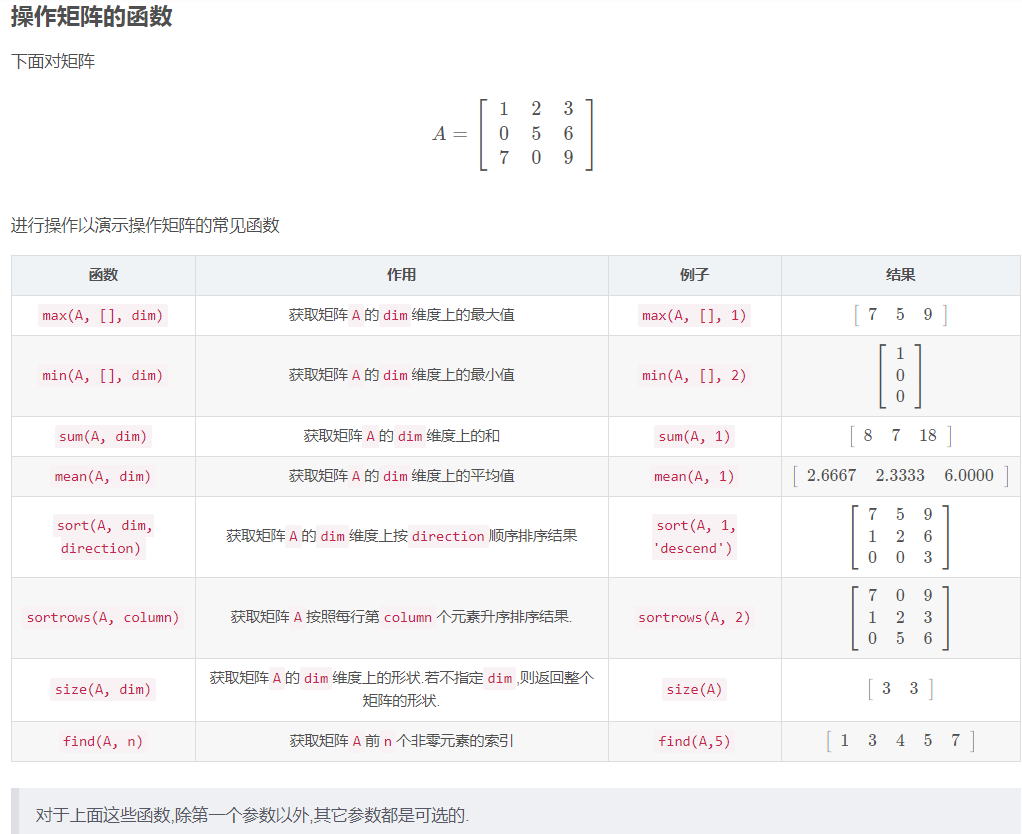
3.矩阵与数组的常用函数 MATLAB提供以下函数来对数组内容进行排序,旋转,排列,重新成形或移位等操作(红色字体需重点掌握).
函数 描述 length 向量的大小或数组的长度 ndims 数组的维数 numel 数组的元素数量 size 数组的维度 iscolumn 确定输入是否为列向量 isempty 确定数组是否为空 ismatrix 确定输入是否为矩阵 isrow 确定输入是否为行向量 isscalar 确定输入是否为标量 isvector 确定输入是否为向量 blkdiag 从输入参数构造块对角矩阵 circshift 循环移位 ctranspose 复共轭转置 diag 矩阵对角矩阵和对角线 flipdim 沿着指定的尺寸翻转数组 fliplr 从左到右翻转矩阵 flipud 向下翻转矩阵 max/min 求数组的最大值/最小值 sum 求数组的和 repmat 复制和平铺数组 reshape 重塑数组(变形) rot90(A,N) 逆时针旋转矩阵A,N*90度 shiftdim 移动维度 issorted 确定设置元素是否按排序顺序 sort 按升序或降序排列数组元素 sortrows 按升序排列行 squeeze 删除单例维度 transpose 转置 vectorize 向量化表达式
3.1 常用函数size( )、numel( )、length( )、ndims( )
(1)size( )函数
s=size(A),当只有一个输出参数时,返回一个行向量,该行向量的第一个元素是 数组的行数,第二个元素是数组的列数。
[r,c]=size(A),当有两个输出参数时,size函数将数组的行数返回到第一个输出变量,将数组的列数返回到第二个输出变量。
如果在size函数的输入参数中再添加一项,并用1或2为该项赋值,则size将返回数组的行数或列数。 其中r=size(A,1)该语句返回的时数组A的行数 , c=size(A,2) 该语句返回的时数组A的列数。
运行下面代码试试看:
A=[1 2 3 4 ; 5 6 7 8 ; 9 10 11 12];
s=size(A)
[r,c]=size(A)
size(A,1)
size(A,2)
输出:
(2)numel( )函数
n=num el (A)该语句返回数组中元素的 总数 。
A=[1 2 3 4 ;
5 6 7 8 ;
9 10 11 12]
t= numel (A)
t =
12
(3)length( )函数
n=length(A):如果A为非空数组, 返回行数和列数两者之间数值较大的那一个值,即相当于执行了max(size(A));
如果A为空数组,则返回0;如果A是一个向量则返回A的长度。
length(A)的功能 相当于max( size(A) ), 若A为非空数组,返回A的最大维数;若A为空数组,返回A中最长的非0维数。
(4)ndims( )函数
ndims(A) 返回数组A的维度的数量。
>> A=rand(3,5,4,3,2);
>> ndims(A)
ans =
5
综合实例:
3.2 数组求和:sum( ) 语法:
S = sum(A)
S = sum(A,'all')
S = sum(A,dim)
S = sum(A,vecdim)
说明:
(1)S = sum(A) 返回 A 沿大小不等于 1 的第一个数组维度的元素之和。
如果 A 是向量
如果 A 是矩阵 列
如果 A 是多维数组,则 sum(A) 沿大小不等于 1 的第一个数组维度计算,并将这些元 素视为向量。此维度会变为 1,而所有其他维度的大小保持不变。
(2) S = sum(A,'all' ) 计算 A 的所有元素的总和。
(3) S = sum(A,dim) 沿维度 dim 返回总和。例如,如果 A 为矩阵,则 sum(A,2) 是包含每一行 列 则 sum(A,1) 是包含每一 列 总和的 行 向量。
(4) S = sum(A,vecdim) 根据向量 vecdim 中指定的维度对 A 的元素求和。例如,如果 A 是矩阵,则 sum(A,[1 2]) 是 A 中所有元素的总和,因为矩阵的每个元素包含在由维度 1 和 2 定义的数组切片中。
例:
%对向量求和
x=1:100;
s_x=sum(x)
%对矩阵求和
a=[1, 2, 3, 4 ;
5, 6, 7, 8 ;
9, 10,11,12]
s_col1=sum(a) %按列 方向求和(默认)
s_col2=sum(a,1 ) %按列 方向求和
s_row=sum(a,2 ) %按 行 方向求和
s_all1=sum(a,'all' ) % 矩 阵所有元素 之和
s_all2=sum( sum(a) ) %求矩阵所有元素之和的方法2(sum函数的嵌套使用)
s_all3=sum( a(:) ) %求矩阵所有元素之和的方法3(把矩阵a展成一长列后再求和)
运行以上代码:
3.3 数组求最值:max()/ min() 这里只拿最大值函数max()举例,最小值函数min( )的用法类 似 。
max:求数组的最大元素
语法:
M = max(A)
M = max(A,[],dim)
[M,I] = max(___)
M = max(A,[],'all')
M = max(A,[],vecdim)
C = max(A,B)
说明:
(1)M = max(A) 返回数组的最大元素。
如果 A 是向量 ,则 max(A) 返回 A 的最大值。
如果 A 为矩阵 ,则 max(A) 是包含每一列的最大值 的行向量。
如果 A 是多维数组,则 max(A) 沿大小不等于 1 的第一个数组维度计算,并将这些元素视为向量。此维度的大小将变为 1,而所有其他维度的大小保持不变。如果 A 是第一个维度长度为零的空数组,则 max(A) 返回与 A 大小相同的空数组。
(2)M = max(A,[],dim) 返回维度 dim 上的最大元素。
例如,如果 A 为矩阵,则 max(A,[],2) 是包含每一行的最大值的列向量。
(3)[M,I] = max(___) 使用先前语法中的任何输入参数,查找 A 的最大值的索引,并在输出 向量 I 中返回这些索引。如果最大值出现多次,则 max 返回对应于第一次出现位置的索引。
(4)M = max(A,[],'all') 查找 A 的所有元素的最大值。
(5) M = max(A,[],vecdim) 计算向量 vecdim 所指定的维度上的最大值。例如,如果 A 是矩阵,则 max(A,[],[1 2]) 计算 A 中所有元素的最大值,因为矩阵的每个元素都包含在由维度 1 和 2 定义的数组切片中。
(6)C = max(A,B) 返回从 A 或 B 中提取的最大元素的数组。
求向量最值:
A = [23 42 37 18 52];
M = max(A)
M = 52
最大复数元素: 创建一个复数向量并计算其最大元素,即具有最大幅值的元素。
A = [-2+2i 4+i -1-3i];
max(A)
ans = 4.0000 + 1.0000i
求矩阵列 中的最大元素: 创建一个矩阵并计算每列中的最大元素。
A = [2 8 4 ;
7 3 9 ];
M = max(A)
M = 1×3
7 8 9
每个矩阵行 中的最大元素: 创建一个矩阵并计算每行中的最大元素。
A = [1.7 1.2 1.5 ;
1.3 1.6 1.99]
M = max(A ,[],2 )
M = 2×1
1.7000
1.9900
最大元素及其索引 : 创建一个矩阵 A 并计算每列中的最大元素,以及这些元素在 A 中显示的行索引。
例:
>> A =randi(30,4,4)
A =
21 14 6 22
10 12 15 23
29 23 14 9
2 24 20 21
>>[M,I] = max( A ) % M表示每一列上的最大值,I表示此最值在这一列上的位置
M =
29 24 20 23
I =
3 4 4 2
求 所有维度上的最大值 ,可以在向量维参数中指定每个维度,或使用 'all' 选项。
b1=randn(4,5)
max(b1,[],'all') %方法1
max(b1,[],[1,2]) %方法2,朝1方向和2方向搜索最大值
max(max(b1)) %方法3
max(b1(:)) %方法4,把b1变为一个列向量,再求最大值
综合实例:
A = randn(6,5)
M1 = max(A)
M2 = max( A, [ ] , 2 )
[m,n] = max(A)
m1=min( min(A) )
m2=min( A(:) )
m3=min( A,[ ],'all' )
3.4 排序数组函数 sort( ) 排序函数sort()的 语法:B = sort(A)
B = sort(A,dim)
B = sort( ___ ,direction)
说明 (1)如果 A 是向量,则 B = sort(A)按升序对 A的元素进行排序。
如果A是矩阵,则 sort(A)会将A的列视为向量并对每列进行排序。
如果A是多维数组,则sort(A)会沿大小不等于 1 的第一个数组维度计算,并将这 些元素视为向量。
(2)B = sort(A,dim) 返回A沿维度dim的排序元素。
例如,如果A是一个矩阵,则 sort(A,2)对每行中的元素进行排序。
(3) B= sort(___,direction) 使用上述任何语法返回按direction指定的顺序显示的A的有序元素。'ascend'表示升序(默认值),'descend'表示降序。
例1 :创建一个行向量,并按升序对其元素排序。
A = [9 0 -7 5 3 8 -10 4 2]; C1 = sort(A,'descend' ) %对行数组A进行降序 C2 = B( end : -1 : 1 ) %对行升序排序得到的数组B,逆向索引后给C2,同样得到降序排序
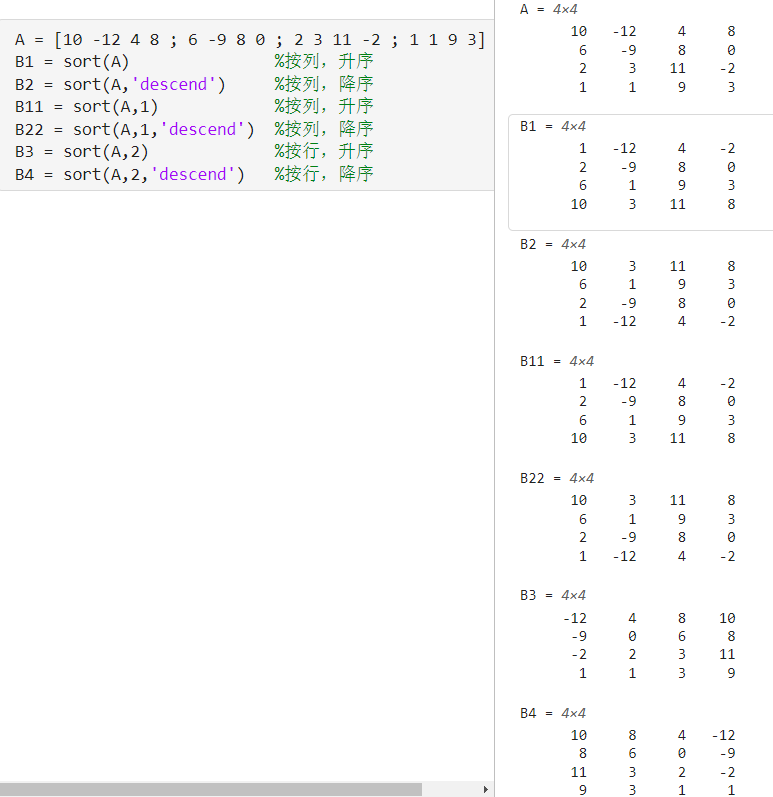
例2: 创建一个矩阵,分别按按 升序 降序 每一 行 /每一列 排序。
A = [10 -12 4 8 ; 6 -9 8 0 ; 2 3 11 -2 ; 1 1 9 3]列 升序 'descend' ) %按列 降序 列 升序 'descend' ) %按列 降序 行 ,升序 'descend' ) %按 行 ,降序
综合练习:
x4 = [10 -12 4 8; 6 -9 8 0; 2 3 11 -2; 1 1 9 3]
lie_max=max(x4) %列最大值
hang_max=max(x4,[],2) %行最大值
all_max=max(x4(:)) %全体最大值
lie_sheng_sort=sort(x4,1 ) %按 列 升序排序
hang_sheng_sort=sort(x4, 2 ) %按 行 升序排序
lie_jiang_sort=sort(x4, 1,' descend ' ) %按 列 降 序排序
hang_jiang_sort=sort(x4, 2 ,' descend ') %按 行 降 序排序
x4 =
10 -12 4 8
6 -9 8 0
2 3 11 -2
1 1 9 3
lie_max =
10 3 11 8
hang_max =
10
8
11
9
all_max =
11
lie_sheng_sort =
1 -12 4 -2
2 -9 8 0
6 1 9 3
10 3 11 8
hang_sheng_sort =
-12 4 8 10
-9 0 6 8
-2 2 3 11
1 1 3 9
lie_jiang_sort =
10 3 11 8
6 1 9 3
2 -9 8 0
1 -12 4 -2
hang_jiang_sort =
10 8 4 -12
8 6 0 -9
11 3 2 -2
9 3 1 1
3.5 数组变形函数——reshape 例1:
已知矩阵A由3×4组成,则 B=reshape(A,2,6)将矩阵A由3×4改变为2×6,并把这个2×6矩阵赋给B;
例2:
B=reshape(A,9,1);将矩阵A由3×3改变为9×1即9行1列(也可以用A(:) ) ,如图:
例3:
x=randperm(50,24)
y1=reshape(x, [4,6] )
y2= reshape(x, [3,4,2] )
x =
37 16 50 21 9 19 45 34 40 14 47 44 36 17 18 27 11 42 15 3 41 22 8 12
y1 =
37 9 40 36 11 41
16 19 14 17 42 22
50 45 47 18 15 8
21 34 44 27 3 12
y2(:,:,1) =
37 21 45 14
16 9 34 47
50 19 40 44
y2(:,:,2) =
36 27 15 22
17 11 3 8
18 42 41 12
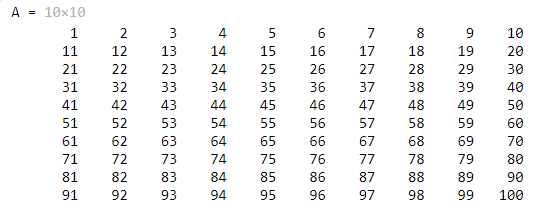
例4: 快速生成按行递增二维数组
A=resh
ape(1:100,10,10)'
3.6 复制和平铺数组 repmat( ) B = rep mat (A,n,m) 返回一个数组,该数组在其 行 维度包含 A 的 n 个副本, 列 维度包含 A 的 m个副本。 A = [ 1 , 2 , 3 ; 4 , 5 , 6 ]
B1 = repmat(A,2,3)
B2 = repmat(A,1,1,2)
A =
1 2 3
4 5 6
B1 =
1 2 3 1 2 3 1 2 3
4 5 6 4 5 6 4 5 6
1 2 3 1 2 3 1 2 3
4 5 6 4 5 6 4 5 6
B2(:,:,1) =
1 2 3
4 5 6
B2(:,:,2) =
1 2 3
4 5 6
3.7 Matlab对矩阵进行旋转、左右上下翻转 END
rot90( ):旋转矩阵 B=rot90(A) % 对矩阵A进行 逆时针 旋转,旋转角度为90度
B=rot90(A,n) % 逆时针旋转n*90度
>> x=reshape( randperm(16) , 4 , 4 )
x =
4 3 9 11
6 7 10 12
1 14 13 16
2 8 15 5
>> y1=rot90(x) % 逆 时针旋转90度
y1 =
11 12 16 5
9 10 13 15
3 7 14 8
4 6 1 2
>> y2=rot90(x, - 1 ) % 顺 时针旋转90度
y2 =
2 1 6 4
8 14 7 3
15 13 10 9
5 16 12 11
>> y3=rot90(x,2 ) % 逆时针旋转180度
y3 =
5 15 8 2
16 13 14 1
12 10 7 6
11 9 3 4
>> y4=rot90( rot90(x ) 嵌套法 逆时针旋转180度
y4 =
5 15 8 2
16 13 14 1
12 10 7 6
11 9 3 4
END
(3)左右、上下翻转 fliplr ()函数 为矩阵左右 翻转
B=flip lr (A)
例:
flipud ()函数 为矩阵上下 翻转
B=flip ud (A)
例:
END
例:字符串的反向输出
已知 str1='I LOVE MATLAB' ;
编写代码反向输出该字符串,既输出str2='BALTAM EVOL I';
方法1:
str1='I LOVE MATLAB'
str2=str1( [ end :-1:1] ) %对str1进行 逆向索引
方法2:
str1='I LOVE MATLAB'
N =length(str1) %利用length()函数得到str1的长度
str2=str1( [ N :-1:1] ) %对str1进行逆向索引
方法3:
str1='I LOVE MATLAB'
3.8 数组元素的循环移位 创建脚本文件并在其中 键入以下代码 -
a = [1 2 3; 4 5 6; 7 8 9] % the original array a b = circshift(a,1) % circular shift first dimension values down by 1. c = circshift(a,[1 -1]) % circular shift first dimension values %down by 1 % and second dimension values to the left % by 1 运行文件文件时,显示以下结果 -
a =
3.9 median( ) 数组的中位数
(1)M = median(A)返回 A 的中位数值。
如果 A 为向量,则 median(A) 返回 A 的中位数值。
如果 A 为非空矩阵,则 median(A) 将 A 的各列视为向量,并返回中位数值的行向量。
如果 A 为 0×0 空矩阵,median(A) 返回 NaN。
如果 A 为多维数组,则 median(A) 将沿大小不等于 1 的第一个数组维度的值视为向量。此维度的大小将变为 1,而所有其他维度的大小保持不变。
median 本身在 A 的数值类中计算,例如 class(M) = class(A)。
(2)M = median(A,'all'):
计算 A 的所有元素的中位数。
(3)M = median(A,dim)
返回维度 dim 上元素的中位数。例如,如果 A 为矩阵,则 median(A,2 行
(4)M = median(A,vecdim)
计算向量 vecdim 所指定的维度上的中位数。例如,如果 A 是矩阵,则 median(A,[1 2]) 是 A 中所有元素的中位数,因为矩阵的每个元素都包含在由维度 1 和 2 定义的数组切片中。
3.10 mean( ) 数组的均值
(1) M = mean(A)
返回 A 沿大小不等于 1 的第一个数组维度的元素的均值。
如果 A 是向量,则 mean(A) 返回元素均值。
如果 A 为矩阵,那么 mean(A) 返回包含每列均值的行向量。
如果 A 是多维数组,则 mean(A) 沿大小不等于 1 的第一个数组维度计算,并将这些元素视为向量。此维度会变为 1,而所有其他维度的大小保持不变。
(2) M = mean(A,'all') 计算 A 的所有元素的均值。
(3) M = mean(A,dim)
返回维度 dim 上的均值。例如,如果 A 为矩阵,则 mean(A,2) 是包含每一行均值的列向量。
(4) M = mean(A,vecdim)
计算向量 vecdim 所指定的维度上的均值。例如,如果 A 是矩阵,则 mean(A,[1 2]) 是 A 中所有元素的均值,因为矩阵的每个元素都包含在由维度 1 和 2 定义的数组切片中。
综合实例:中位数与均值的区别
%数组时=======
>> x=[1.1,1.2,1.3,1.4,1.5,3,12,50,99]
x =
1.1000 1.2000 1.3000 1.4000 1.5000 3.0000 12.0000 50.0000 99.0000
>> y1=median(x) %中位数
y1 =
1.5000
>> y2=mean(x) %均值
y2 =
18.9444
%矩阵时 =======
a=randi(100,9,5)'
md1=median(a)
md2=median(a,2)
md_all=median(a,'all')
me1=mean(a)
me2=mean(a,2)
me_all=mean(a,'all')
运行上面代码:
a =
8 24 13 19 24 42 5 91 95
50 49 34 91 37 12 79 39 25
41 10 14 95 96 58 6 24 36
83 2 5 17 65 74 65 46 55
30 75 19 69 19 37 63 79 9
md1 =
41 24 14 69 37 42 63 46 36
md2 =
24
39
36
55
37
md_all =
37
me1 =
42.4000 32.0000 17.0000 58.2000 48.2000 44.6000 43.6000 55.8000 44.0000
me2 =
35.6667
46.2222
42.2222
45.7778
44.4444
me_all =
42.8667
3.11 diag()函数
diag()
语法
D = diag(v)
D = diag(v,k)
x = diag(A)
x = diag(A,k)
D = diag(v) 返回主对角线为 向量 v 的对角矩阵。
D = diag(v,k) 将向量 v
x = diag(A) 返回 由 矩阵 A 列 向量。
x = diag(A,k) 返回 由 矩阵 A 组成的 列 向量。
(1)使用 diag 创建一个包含 向量v 在主对角线上的元素的矩阵。
创建一个 1×5 的向量。
v = [2 1 -1 -2 -5];
D = diag(v)
D = 5×5
2 0 0 0 0
0 1 0 0 0
0 0 -1 0 0
0 0 0 -2 0
0 0 0 0 -5
(2)创建一个包含 向量
D1 = diag(v,1)
D1 = 6×6
0 2 0 0 0 0
0 0 1 0 0 0
0 0 0 -1 0 0
0 0 0 0 -2 0
0 0 0 0 0 -5
0 0 0 0 0 0
结果为一个 6×6 矩阵。将一个长度为 n 的向量指定为输入时,diag 返回一个大小为 n+abs(k) 的方阵。
(3)获取矩阵的对角线元素
获取一个随机 6×6 矩阵的主对角线上的元素。
A = randi(10,6)
A = 6×6
9 3 10 8 7 8
10 6 5 10 8 1
2 10 9 7 8 3
10 10 2 1 4 1
7 2 5 9 7 1
1 10 10 10 2 9
x = diag(A)
x = 6×1
9
6
9
1
7
9
(4)获取矩阵 A 的第一个下对角线 (k=-1) 上的元素。
结果比主对角线少一个元素。
x1 = diag(A,-1)
x1 = 5×1
10
10
2
9
2
(5)调用 diag 两次将返回一个包含原始矩阵的对角元素的对角矩阵。
A1 = diag(diag(A))
A1 = 6×6
9 0 0 0 0 0
0 6 0 0 0 0
0 0 9 0 0 0
0 0 0 1 0 0
0 0 0 0 7 0
0 0 0 0 0 9
练习:生产 7×7的魔方矩阵a,求矩阵a的每行的平均值和中位数,求矩阵a的每行的和/每列的和/两条对角线的和。
a=magic(7)
m1=mean(a,2)
m2=median(a,2)
s1=sum(a)
s2=sum(a,2)
v1=diag(a)
v2=diag(rot90(a))
s_v1=sum(v1)
s_v2=sum(v2)
练习: 创建一个3×3魔方阵和3×3 的随机矩阵,将两个矩阵拼接起来。然后提取任意元素。
clear;
clc;
mat1 = magic(3)
mat2 = rand(3,3)
mat3 = [mat1 , mat2] %横向拼接
mat4 = [mat1 ; mat2] %纵向拼接
mat5 = mat3(2:3,[1,3,4]) %提取第2、3行,第1、3、4列的元素
mat6 = mat3([1,3],[2,4])
=================================
=================================
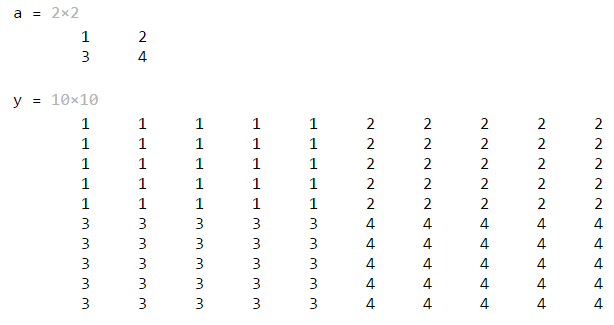
作业1:编程实现把任何一个输入的2*2的矩阵a变成10*10的矩阵y
要求效果如下:
提示,有两种方法。
方法1:采用repmat函数;
方法2:采用如下索引方式
作业2:
(1)先把A和B按纵向合成为一个6*3的矩阵C,然后再把C的3个列向量串接成一个18*1的列向量D,然后把D再变为一个1*18的 行向量E。
(2)把上一步得到的行向量E,采用reshape函数变形为一个2*9的新矩阵F;
(3)采用cat()函数把 A和B合并成一个3*3*2的三维数组G。
作业3: (1) 创建一个5*10*3的 随机 整数三维数组,要求所有元素都是1-150之间的整数,且 不许重复(提示:使用 randperm函数 ) ;(2)先求每一面 最大值 和最小 值,再求 整个矩阵的最大值和最小值 ;
作业4: (1)创建5*10的符合正态分布(均值为0)的随机矩阵a。(2)分别对a矩阵的 行 方向进行 升序 排序得到矩阵B,再对B矩阵的列方向 降序 排序 得到矩阵C 。(3)求这个C矩阵所有元素之和,以及 元素的 平均值。
作业5: (1)创建5*5的魔方矩阵a ;(2)对矩阵a 先进行 顺 时针90°的旋转,再 上下 翻转后得到矩阵b;(3)验证得到的这个新矩阵b 的,各行之和, 各 列之和,左对角线之和(提示:需要把对角线元素一个个都索引出来,作为一个行向量,再来求和 ),右对角线之和,看看这些和是否相等?
作业6: 生成一个400*400像素的纯色图(颜色调节到自己喜欢的状态)。提示,采用ones()/cat() 等函数生成400*400*3的三维数组,作为RGB三个通道的数据,然后用 imshow()函数显示这个数组。
===================================
本节重要函数总结:
随机数函数课外扩展:
(1)
unifrnd (a,b); 产生一个[a,b]的均匀随机数; unif rnd 是 unif orm ra nd om的缩写。
unifrnd (a, b, m, n); 产生m*n阶[a, b]均 匀分布;
(2)
binornd(n,p,[M,N,P,…]) 产生的是服从二项分布的随机数,二项分布的参数为:n和p,
考虑一个打靶的例子,每枪命中率为p,共射击N枪,那么一共击中的次数就服从参数为(N,p)的二项分布。其中p要小于等于1且非负,N要为整数;;
binornd(n,p,[M,N,P,…]) 生成的随机数服从参数为(N,p)的二项分布,这些随机数排列成MNP… 阶矩阵。如果只写M,则生成M*M矩阵;
(3)
exprnd (mu ,m, n)产生m*n阶期望值为mu的指数分布的随机数矩阵;
exprnd 是 expectation random的缩写。
常见分布的随机数产生 函数名
调用形式
注 释
Unifrnd
unifrnd ( A,B,m,n)
[A,B]上均匀分布(连续) 随机数
Unidrnd
unidrnd(N,m,n)
均匀分布(离散)随机数
Exprnd
exprnd(Lambda,m,n)
参数为Lambda的指数分布随机数
Normrnd
normrnd(MU,SIGMA,m,n)
参数为MU,SIGMA的正态分布随机数
chi2rnd
chi2rnd(N,m,n)
自由度为N的卡方分布随机数
Trnd
trnd(N,m,n)
自由度为N的t分布随机数
Frnd
frnd(N1 , N2 ,m,n)
第一自由度为N1 ,第二自由度为N2 的F分布随机数
gamrnd
gamrnd(A, B,m,n)
参数为A, B的
betarnd
betarnd(A, B,m,n)
参数为A, B的
lognrnd
lognrnd(MU, SIGMA,m,n)
参数为MU, SIGMA的对数正态分布随机数
nbinrnd
nbinrnd(R, P,m,n)
参数为R,P的负二项式分布随机数
ncfrnd
ncfrnd(N1 , N2, delta,m,n)
参数为N1 ,N2 ,delta的非中心F分布随机数
nctrnd
nctrnd(N, delta,m,n)
参数为N,delta的非中心t分布随机数
ncx2rnd
ncx2rnd(N, delta,m,n)
参数为N,delta的非中心卡方分布随机数
raylrnd
raylrnd(B,m,n)
参数为B的瑞利分布随机数
weibrnd
weibrnd(A, B,m,n)
参数为A, B的韦伯分布随机数
binornd
binornd(N,P,m,n)
参数为N, p的二项分布随机数
geornd
geornd(P,m,n)
参数为 p的几何分布随机数
hygernd
hygernd(M,K,N,m,n)
参数为 M,K,N的超几何分布随机数
Poissrnd
poissrnd(Lambda,m,n)
参数为Lambda的泊松分布随机数


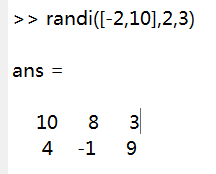













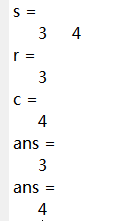


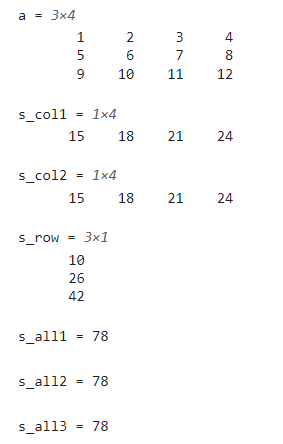


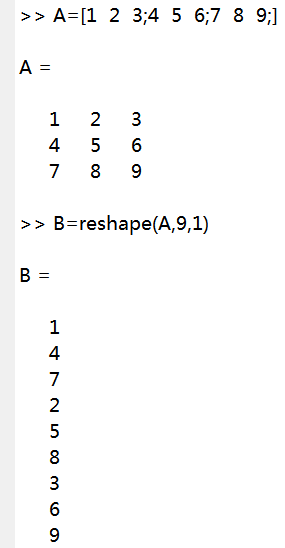


 、
、