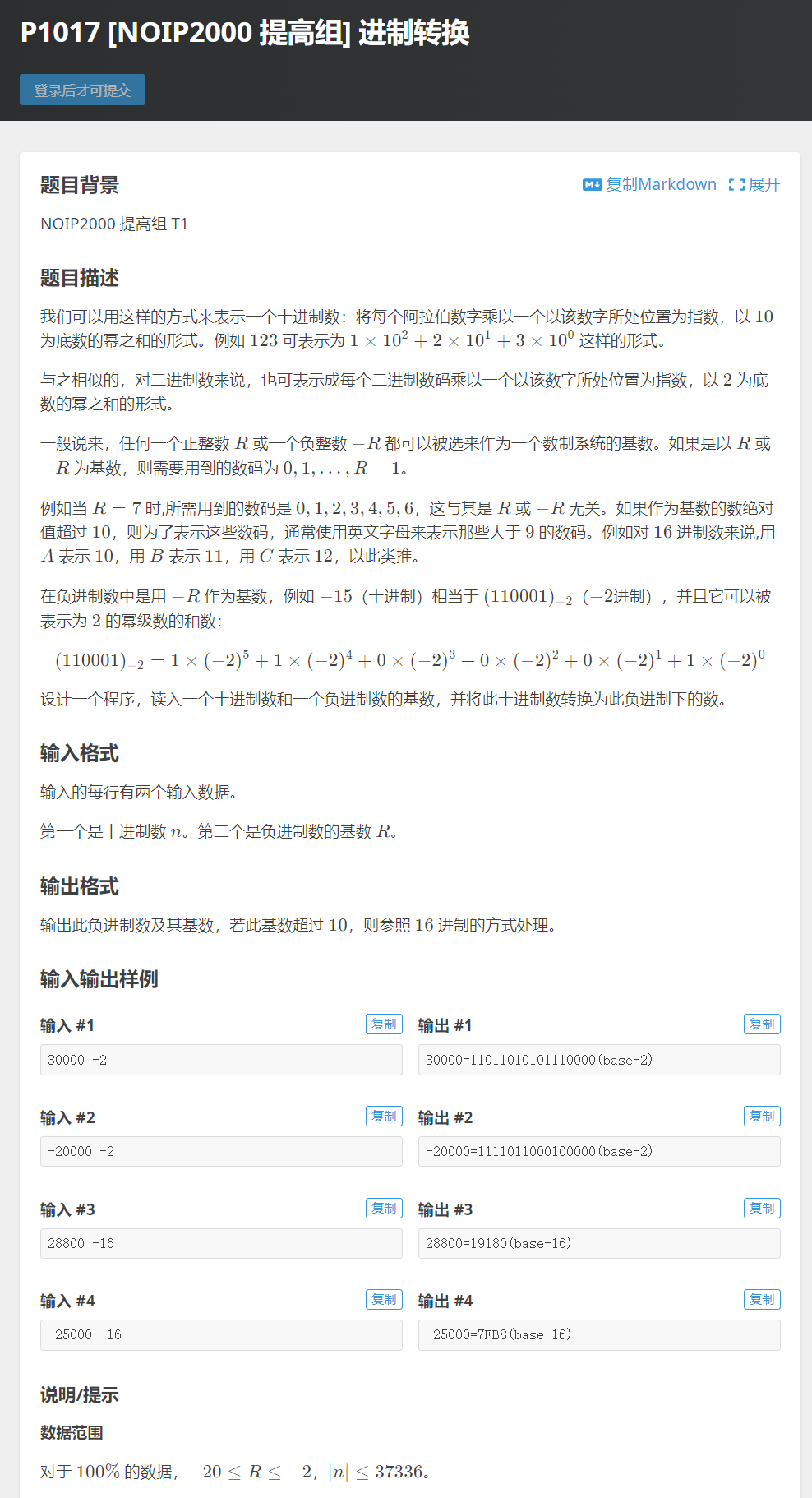
编程练习网站： https://projecteuler.net/archives

https://www.ilovematlab.cn/forum.php

信用卡校验

当你输入信用卡号码的时候，有没有担心输错了而造成损失呢？其实可以不必这么担心，因为并不是一个随便的信用卡号码都是合法的，它必须通过Luhn算法来验证通过。

该校验的过程：

1、从卡号最后一位数字开始，逆向将奇数位(1、3、5等等)相加。

2、从卡号最后一位数字开始，逆向将偶数位数字，先乘以2（如果乘积为两位数，则将其减去9），再求和。

3、将奇数位总和加上偶数位总和，结果应该可以被10整除。

例如，卡号是：5432123456788881

逆向奇数位为 4 2 2 4 6 8 8 1 和 = 35

逆向偶数位乘以2（有些要减去9）的结果：1 6 2 6 1 5 7 7，求和 = 35。

最后 35 + 35 = 70 可以被10整除，认定校验通过。

请编写一个程序，从标准输入获得卡号，然后判断是否校验通过。

通过显示：“成功”，否则显示“失败”。

比如，

输入：356827027232780

程序输出：成功

立方和等式

考虑方程式：a^3 + b^3 = c^3 + d^3

其中：“^”表示乘方。a、b、c、d是互不相同的小于30的正整数。

这个方程有很多解。比如：

a = 1，b=12，c=9，d=10 就是一个解。因为：1的立方加12的立方等于1729，而9的立方加10的立方也等于1729。

当然，a=12，b=1，c=9，d=10 显然也是解。

如果不计abcd交换次序的情况，这算同一个解。

你的任务是：找到所有小于30的不同的正整数解。把a b c d按从小到大排列，用逗号分隔，每个解占用1行。比如，刚才的解输出为：

1,9,10,12

不同解间的顺序可以不考虑。

1、分红酒

  有4个红酒瓶子，它们的容量分别是：9升, 7升, 4升, 2升

  

  开始的状态是 [9,0,0,0]，也就是说：第一个瓶子满着，其它的都空着。

  允许把酒从一个瓶子倒入另一个瓶子，但只能把一个瓶子倒满或把一个瓶子倒空，不能有中间状态。这样的一次倒酒动作称为1次操作。

  假设瓶子的容量和初始状态不变，对于给定的目标状态，至少需要多少次操作才能实现？

  本题就是要求你编程实现最小操作次数的计算。

 

  输入：最终状态（逗号分隔）

  输出：最小操作次数（如无法实现，则输出-1）

例如：

输入：

9,0,0,0

应该输出：

0

输入：

6,0,0,3

应该输出：

-1

输入：

7,2,0,0

应该输出：

2

第39级台阶

    小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!

    站在台阶前，他突然又想着一个问题：

    如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？

    请你利用计算机的优势，帮助小明寻找答案。

要求提交的是一个整数。

注意：不要提交解答过程，或其它的辅助说明文字。

匪警请拨110

匪警请拨110,即使手机欠费也可拨通！

    为了保障社会秩序，保护人民群众生命财产安全，警察叔叔需要与罪犯斗智斗勇，因而需要经常性地进行体力训练和智力训练！

    某批警察叔叔正在进行智力训练：

    1 2 3 4 5 6 7 8 9 = 110;

    请看上边的算式，为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法；123+4+5+67-89 是另一个可能的答案。

    请你利用计算机的优势，帮助警察叔叔快速找到所有答案。

    每个答案占一行。形如：

12+34+56+7-8+9

123+4+5+67-89

......

    已知的两个答案可以输出，但不计分。

   

    各个答案的前后顺序不重要。

123+4+5+67-89=110

123+4-5-6-7-8+9=110

123-4+5-6-7+8-9=110

123-4-5+6+7-8-9=110

12+34+56+7-8+9=110

12+3+45+67-8-9=110

12-3+4-5+6+7+89=110

1+234-56-78+9=110

1+2+34+5+67-8+9=110

1-2+3+45-6+78-9=110

clear

x=['1','2','3','4','5','6','7','8','9'];

y=['+','-','*'];

for n1=1:3

    if y(n1)=='*'

        z1=[x(1),x(2)];

    else

        z1=[x(1),y(n1),x(2)];

    end

    

    for n2=1:3

        if y(n2)=='*'

            z2=[z1(:)',x(3)];

        else

            z2=[z1(:)',y(n2),x(3)];

        end

        

        for n3=1:3

            if y(n3)=='*'

                z3=[z2(:)',x(4)];

            else

                z3=[z2(:)',y(n3),x(4)];

            end

           

            for n4=1:3

                if y(n4)=='*'

                    z4=[z3(:)',x(5)];

                else

                    z4=[z3(:)',y(n4),x(5)];

                end   

                            

                for n5=1:3

                    if y(n5)=='*'

                        z5=[z4(:)',x(6)];

                    else

                        z5=[z4(:)',y(n5),x(6)];

                    end      

 

                    for n6=1:3

                        if y(n6)=='*'

                            z6=[z5(:)',x(7)];

                        else

                            z6=[z5(:)',y(n6),x(7)];

                        end

                

                        for n7=1:3

                            if y(n7)=='*'

                                z7=[z6(:)',x(8)];

                            else

                                z7=[z6(:)',y(n7),x(8)];

                            end

                    

                            for n8=1:3

                                

                                if y(n8)=='*'

                                    z8=[z7(:)',x(9)];

                                else

                                    z8=[z7(:)',y(n8),x(9)];

                                end

                                

                                L=length(z8);

                                z='';

                                

                                for m=1:L

                                    z=strcat(z,z8(m));

                                end

                                if eval(z)==110

                                   disp(z)

                                end                  

                            end

                        end

                    end

               end           

            end          

        end

    end

end

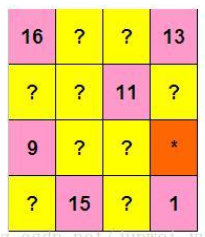
幻方填空

    幻方是把一些数字填写在方阵中，使得行、列、两条对角线的数字之和都相等。

    欧洲最著名的幻方是德国数学家、画家迪勒创作的版画《忧郁》中给出的一个4阶幻方。

    他把1,2,3,...16 这16个数字填写在4 x 4的方格中。

    表中有些数字已经显露出来，还有些用?和*代替。


    请你计算出? 和 * 所代表的数字。并把 * 所代表的数字作为本题答案提交。

clear

y=[2 3 4 5 6 7 8 10 12 14];

yperms=perms(y);  %对y进行全排列

n=length(yperms)

s=34;                      %4阶魔方的每列每行之和必为34，sum([1:16])/4

for k=1:n

    x=yperms(k,:);

    eq1=x(1)+x(2)+29-s;

    eq2=x(3)+x(4)+x(5)+11-s;

    eq3=x(6)+x(7)+x(8)+9-s;

    eq4=x(9)+x(10)+16-s;

    eq5=x(3)+x(9)+25-s;

    eq6=x(1)+x(4)+x(6)+15-s;

    eq7=x(2)+x(7)+x(10)+11-s;

    eq8=x(5)+x(8)+14-s;

    eq9=x(4)+x(7)+17-s;

    eq10=x(6)+x(9)+24-s;

    if (eq1==0)&(eq2==0)&(eq3==0)&(eq4==0)&(eq5==0)&...

       (eq6==0)&(eq7==0)&(eq8==0)&(eq9==0)&(eq10==0)

       x

    end

end

全排列：

x=[1 2 3 4 ]

L=length(x);

myperm(x,1,L)

function myperm(str,n1,n2)

if n1==n2

    str

else

    for k=n1:n2

        temp=str(n1);str(n1)=str(k);str(k)=temp;

        myperm(str,n1+1,n2);

        

    end

end

end

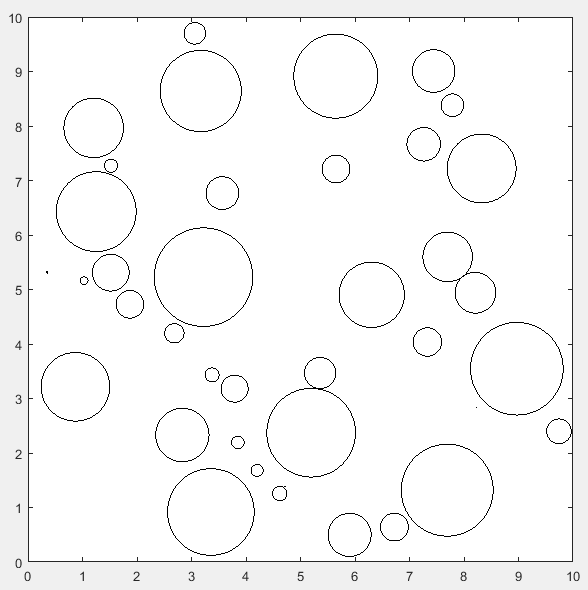
如何生成随机圆图案：

clear;

clc;

close all;

% 限定范围

width = 10;  

height = 10;

% 最多产生的圆的个数

circleNumber = 100;   

% 记录每个圆的横坐标、纵坐标、半径

paras = zeros(circleNumber, 3);  

num = 0;

hold on

while num < circleNumber

    num = num + 1;    

    % 圆半径小于1或者设定为固定值

    r = rand; 

    % 在范围内随机坐标

    xPos = rand*(width-2*r) + r;  

    yPos = rand*(height-2*r) + r;

    % 记录坐标、半径

    paras(num,:) = [xPos, yPos, r];

    % 判断每个圆的位置是否不相切、不相交

    if num > 1

        % 新产生的圆和之前产生的所有圆计算距离        

        xs = paras(1:num - 1, 1);

        ys = paras(1:num - 1, 2);

        rs = paras(1:num - 1, 3);

        dist1 = sqrt((xPos - xs).^2 + (yPos - ys).^2);

        dist2 = abs(r + rs);

        % 如果相离则绘制当前产生的圆，否则就重新生成一个圆

        if all(dist1 > dist2)

            rectangle('Position', [xPos-r, yPos-r, 2*r, 2*r], 'Curvature', [1 1]);

            axis equal

        else

            r = rand; 

            xPos = rand*(width-2*r) + r;  

            yPos = rand*(height-2*r) + r;

            paras(num,:) = [xPos,yPos,r];

            % 防止死循环

            temp = 0;

            maxTry = 100;

            while any(dist1 <= dist2) && temp < maxTry

                temp = temp + 1;

                dist1 = sqrt((xPos - xs).^2 + (yPos - ys).^2);

                dist2 = abs(r + rs);

            end

            if all(dist1 > dist2)

                rectangle('Position', [xPos-r, yPos-r, 2*r, 2*r], 'Curvature', [1 1]);

                axis equal

            end

        end      

    end

end

axis([0 width 0 height])

box on

hold off

leetcode-最大子序和(四种)

https://blog.csdn.net/zwzsdy/article/details/80029796

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],

输出: 6

解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

这道题在LeetCode中被归类为简单类，但是，却有三种甚至更多的解法，值得探讨。

1.暴力破解法——时间效率O(N^3)，超时
这是最容易想到的，通过枚举判断。

    private int max = Integer.MIN_VALUE;

    public int maxSubArray(int[] nums) {

        int sum;

        for (int i = 0; i < nums.length; i++) {// 子序列左端点

            for (int j = i; j < nums.length; j++) {// 子序列右端点

                sum = 0;

                for (int k = i; k <= j; k++) {//暴力计算

                    sum += nums[k];

                }

                if (sum > max) {

                    max = sum;

                }

            }

        }

        return max;

    }

2.改进暴力法——时间效率O(N^2)
其实我们可以发现，每次我们都是重复计算了一部分子序列，即当我计算前两个时，第三次我还是会计算前两个在加第三个，这样就造成了O(N^3)，现在我们根据前一次的进行计算，那么将会减少一层循环。

    private int max = Integer.MIN_VALUE;

    public int maxSubArray(int[] nums) {

        int sum;

        for (int i = 0; i < nums.length; i++) {// 子序列左端点

            sum = 0;

            for (int j = i; j < nums.length; j++) {// 子序列右端点

                sum += nums[j];// 这里就相当于每次根据前一次的序列来计算新的序列

                if (sum > max)

                    max = sum;

            }

        }

        return max;

    }

3.扫描法——O(N)

当我们加上一个正数时，和会增加；当我们加上一个负数时，和会减少。如果当前得到的和是个负数，那么这个和在接下来的累加中应该抛弃并重新清零，不然的话这个负数将会减少接下来的和。

据说这道题是《编程珠机》里面的题目，叫做扫描法，速度最快，扫描一次就求出结果，复杂度是O（n）。书中说，这个算法是一个统计学家提出的。

这个算法如此精炼简单，而且复杂度只有线性。但是我想，能想出来却非常困难，而且证明也不简单。在这里，我斗胆写出自己证明的想法：

关于这道题的证明，我的思路是去证明这样的扫描法包含了所有n^2种情况，即所有未显示列出的子数组都可以在本题的扫描过程中被抛弃。

1 首先，假设算法扫描到某个地方时，始终未出现加和小于等于0的情况。

我们可以把所有子数组（实际上为当前扫描过的元素所组成的子数组）列为三种：

1.1 以开头元素为开头，结尾为任一的子数组

1.2 以结尾元素为结尾，开头为任一的子数组

1.3 开头和结尾都不等于当前开头结尾的所有子数组

1.1由于遍历过程中已经扫描，所以算法已经考虑了。1.2确实没考虑，但我们随便找到1.2中的某一个数组，可知，从开头元素到这个1.2中的数组的加和大于0（因为如果小于0就说明扫描过程中遇到小于0的情况，不包括在大前提1之内），那么这个和一定小于从开头到这个1.2数组结尾的和。故此种情况可舍弃

1.3 可以以1.2同样的方法证明，因为我们的结尾已经列举了所有的情况，那么每一种情况和1.2是相同的，故也可以舍弃。

2 如果当前加和出现小于等于0的情况，且是第一次出现，可知前面所有的情况加和都不为0

一个很直观的结论是，如果子段和小于0，我们可以抛弃，但问题是是不是他的所有以此子段结尾为结尾而开头任意的子段也需要抛弃呢？

答案是肯定的。因为以此子段开头为开头而结尾任意的子段加和都大于0（情况2的前提），所以这些子段的和是小于当前子段的，也就是小于0的，对于后面也是需要抛弃的。也就是说，所有以之前的所有元素为开头而以当前结尾之后元素为结尾的数组都可以抛弃了。

而对于后面抛弃后的数组，则可以同样递归地用1 2两个大情况进行分析，于是得证。

class Solution {

    public int maxSubArray(int[] nums) {

        int current=nums[0];

        int sum=nums[0];

        //我们考虑如果全是负数，那么返回最大的负数，如果最后的和为正，那么就使用扫描法

        for(int i=1;i<nums.length;i++) {

            if(current<0)current=nums[i];//当前数小于0 肯定会舍去（否则将会影响接下来的和），换为下一个数

            else current+=nums[i];//如果当前数不小于0，那么他会对接下来的和有积极影响

            if(current>sum)sum=current;//这里既实现了负数返回最大也实现了扫描法

            //这里其实已经隐式的列举了所有可能，保留了所有可能的最大值

        }

        return sum;

    }

}

4.动态规划法——O(N)

设sum[i]为以第i个元素结尾且和最大的连续子数组。假设对于元素i，所有以它前面的元素结尾的子数组的长度都已经求得，那么以第i个元素结尾且和最大的连续子数组实际上，要么是以第i-1个元素结尾且和最大的连续子数组加上这个元素，要么是只包含第i个元素，即sum[i]

= max(sum[i-1] + a[i], a[i])。可以通过判断sum[i-1] + a[i]是否大于a[i]来做选择，而这实际上等价于判断sum[i-1]是否大于0。由于每次运算只需要前一次的结果，因此并不需要像普通的动态规划那样保留之前所有的计算结果，只需要保留上一次的即可，因此算法的时间和空间复杂度都很小

class Solution {

    public int maxSubArray(int[] nums) {// 动态规划法

        int sum=nums[0];

        int n=nums[0];

        for(int i=1;i<nums.length;i++) {

            if(n>0)n+=nums[i];

            else n=nums[i];

            if(sum<n)sum=n;

        }

        return sum;

    }

}

5.解题思路

定义当前子序和以及最大子序和为数组的一个元素；

遍历整数数组，比较当前子序和的值及当前遍历的值，取较大值重置赋值给当前子序和 cur_sum；

同时比较当前子序和及最大子序和的值，取较大值重置赋值给最大子序和 max_sum；

遍历结束，返回最大子序和的值 max_sum。

class Solution:

    def maxSubArray(self, nums: List[int]) -> int:

        '''查找连续子数组的最大和

        Args:

            nums: 整数数组

        

        Returns:

            返回整数数组的最大子序和

        '''

        # 比较当前子序和，最大子序和，返回最大值

        # 定义当前子序和以及最大子序和为第一个元素

        cur_sum = max_sum = nums[0]

        # 遍历整数数组

        for x in range(1, len(nums)):

            # 比较当前值和当前子序和的值，取较大值

            cur_sum = max(nums[x], cur_sum + nums[x])

            # 比较当前值和定义的最大子序和值，将最大值重置赋值给 max_sum

            max_sum = max(cur_sum, max_sum)

        return max_sum

            

很多人对这道题最开始都会有一个误区，就是 只要将连续的正数相加就肯定是最大的

这种思想当然是有问题的 最简单的例子 1, 2, 3, -99, 100000 如果用刚才那样想法求出的最大和是6，但是答案肯定是不对的

应该是最后一项数

所以这就引出了一种思想：

如果当前和大于0，则加上下一个数（当前和是正的 对后面的求和“有益处”）

如果当前和小于或等于0，则将下一个数赋给当前和

最后比较当前和与存储最大值的变量 取最大值

%崔春雷提供代码

str=[-2,1,-3,4,-1,2,1,-5,4,3,-1,2,-5,2,-3,4];

s_temp=0;

s_all=0;

for k=str

    if s_temp>0  %如果过去为正资产，则保留过去，同时拥抱未来。哪怕未来是负的，只要这个负不是很严重到可以把过去的正全部抵消，则一直保留过去，拥抱未来。

       s_temp=s_temp+k;

    else   %如果之前的s_temp位负资产，则舍弃过去，拥抱未来（哪怕未来也是负的，未来一个负总比过去的负加上未来的负强，如果未来是正的，更要拥抱）

        s_temp=k;

    end

    s_all=max(s_all,s_temp); %不断选择其中最大的

end

s_all

1、令S = {2，3，5，...，4999}是小于5000的质数的集合。

求出S的子集数，S的子项之和为素数。

求16位数的最大值作为答案。

%%MATLAB的向量化版:

function SUM = euler0249

tic;

M = int64(1e16);

p_set = primes(4999)';

s = cumsum(p_set);

p_set2 = primes(s(end));

cnt = zeros(s(end) + 1, 1, 'int64');

cnt(1) = 1;

for ii = 1:numel(p_set)

    p = p_set(ii);

    jj = p+1:s(ii)+1;

    cnt(jj) = mod(cnt(jj) + cnt(jj-p), M);

end

cnt2 = cnt(p_set2+1);

SUM = 0;

for ii = 1:numel(cnt2)

    SUM = mod(SUM + cnt2(ii), M);

end

toc;

end

2.求100万内所有素数之和。

3.

斐波那契数列中的每个新项都是通过将前两个项相加而生成的。从1和2开始，前10个项将是：

1，2，3，5，8，13，21，34，55，89，...

通过考虑斐波那契数列中值不超过400万的项，找到偶值项的总和。

4.

克里斯蒂安·戈德巴赫（Christian Goldbach）提出，每个奇数复合数字都可以写成一个素数和一个平方的两倍的和。

9 = 7 + 2×1 ²
15 = 7 + 2×2 ²
21 = 3 + 2×3 ²
25 = 7 + 2×3 ²
27 = 19 + 2×2 ²
33 = 31 + 2×1 ²

事实证明，这种猜想是错误的。

不能写为素数和平方的两倍的最小奇数复合物是什么？

%code：

clear all

clc

for k=10:3000   

      x=2*k+1;

      flag=0;

    if  isprime(x)==0     

        pri=primes(x);

        L=length(pri)

            

        for jj=1:L  

          

            if  rem(  sqrt( (x-pri(jj))/2 ) ,1)==0             

                 flag=flag+1;

                 break;           

            end

            

        end

        

        if  flag==0        

            fprintf('find the num=%d\n',x)         

            break;         

        end

        

    end

    

end

5.

质数41可以写为六个连续质数之和：

41 = 2 + 3 + 5 + 7 + 11 + 13

这是100内可以写成连续质数和的最长总和。1000内可以写成连续质数和的最长总和所对应的数为953，可以写成21个项之和。

那么，哪一个素数（一百万内）可以写为最长连续的素数之和？

%code：

clear all

clc

pri=primes(1000);

L=length(pri);

Q=0；

N=1;

while m<=L

s=0;

for k=N:L

      s= s+pri(k);

      Q(m)=Q(m)+1；

      if  isprime(s)==0

          N=N+1;

          break;

       end

end

未完成。。

   先说正向求解：
就是先生成100万以下的质数列表，然后依次从列表末端提取质数进行判断（因为通常越长的连续质数链意味着越大的和），如果某个质数是某段连续质数的和，取得质数链的个数，则始终保存最长质数链。大致思路就是这样。    

#coding:utf-8

'''Find the longest prime-chain sum which is also a prime below 1000000'''

import time

timestart = time.time()

primes = [True] * 1000000

primes[0],primes[1] = False,False

for i,prime in enumerate(primes):

    if prime:

        for j in range(i*i,1000000,i):

            primes[j] = False

plist = [k for k,trueprime in enumerate(primes) if trueprime]

longest, longestprime = 1, 2

while len(plist)>1:

    testprime = plist.pop()

    window_start = 0

    window_end = window_start + longest

    while sum(plist[window_start:window_end]) < testprime:

        window_end += 1

    if window_end == window_start + longest:

        break

    if sum(plist[window_start:window_end]) == testprime:

        if window_end-window_start > longest:

            longest = window_end-window_start

            longestprime = testprime

            break

    else:

        window_end -= 1

        while window_end>window_start+longest:

            flag = 0

            ws, we = window_start, window_end

            while we < len(plist)-1:

                if sum(plist[ws:we]) == testprime:

                    flag = 1

                    if we - ws > longest:

                        longest = we - ws

                        longestprime = testprime

                        break

                elif sum(plist[ws:we]) > testprime:

                    break

                we += 1

                ws += 1

            if flag:

                break

            else:

                window_end -= 1

print('Found the longest chain, which is %d with %d primes sum' % (longestprime, longest+1))

print('Time used: %.3f sec' % (time.time()-timestart))

再说反向求解：
就是先求得100万以下最长的质数链有多少个，然后再依次缩小质数链的长度，直到某个质数链的和正好也是质数。则这个质数链就是最长的质数链。
这个解法的好处就是只要求得第一个解，就是我们要找的最值，所以速度很快。

#coding:utf-8

'''Find the longest prime-chain sum which is also a prime below 1000000'''

import time

timestart = time.time()

primes = [True] * 1000000

primes[0],primes[1] = False,False

for i,prime in enumerate(primes):

    if prime:

        for j in range(i*i,1000000,i):

            primes[j] = False

plist = [k for k,trueprime in enumerate(primes) if trueprime]

# set max window size

window = 1

while sum(plist[:window]) < 1000000:

    window += 1

# moving window

while window > 1:

    # moving window start and end

    start = 0

    end = start + window

    # move till the end of prime list

    while end < len(plist):

        # test: always true, is sum of primes

        tmp = sum(plist[start:end])

        # too big, skip

        if tmp > 1000000:

            break

        # test: is prime, < n

        elif tmp < 1000000 and tmp in plist:

            print('Found the longest chain, which is %d with %d primes sum' % (tmp, window))

            print('Time used: %.3f sec' % (time.time()-timestart))

            exit()

        # sliding window

        start += 1

        end = start + window - 1

    # try next window size

    window -= 1

---------------------

from time import time st=time() def pr(n):#定义一个质数     if n==2:return True     for i in range(2,int(n**0.5)+1):         if n%i==0:             return False     return True n = 2 a = [] while True:#求出 连续质数和小于100w的质数     if pr(n):         a.append(n)     if sum(a)>1000000:         break     n+=1 def main():     le=len(a)     j=le     while j:         for k in reversed(range(0,le+1-j)):             y=sum(a[k:k+j])#在满足范围内求出连续质数和             # print(y)             if y<1000000:#质数和小于100w 且和为质数的数                 if pr(y):                     return y         j-=1 y=main() print(y) print(time()-st)

6.

7.

最长的Collatz序列

问题14

为正整数的集合定义了以下迭代序列：

n → n / 2（n为偶数）
n →3 n +1（n为奇数）

使用上面的规则并从13开始，我们生成以下序列：

13→40→20→10→5→16→8→4→2→1

可以看出，该序列（从13开始到1结束）包含10个项。尽管尚未得到证明（Collatz问题），但可以认为所有起始数字都以1结尾。

最长的链条中小于100万的哪个起始数字？

注意：连锁店一旦启动，条款就可以超过一百万。

8.

最大素数

问题3

13195的主要因子是5、7、13和29。既：13195=5*7*13*29

数字600851475143中最大的素数因子是多少？

9.

数字阶乘

问题34

145是一个奇数，等于1！+ 4！+ 5！= 1 + 24 + 120 = 145。

查找所有数字的总和，这些数字等于其数字的阶乘之和。

注意：作为1！= 1和2！= 2不是总和，不包括在内。

10

数字五次幂

问题30

令人惊讶的是，只有三个数字可以写为它们的数字的四次幂之和：

1634 = 1 ⁴ + 6 ⁴ + 3 ⁴ + 4 ⁴
8208 = 8 ⁴ + 2 ⁴ + 0 ⁴ + 8 ⁴
9474 = 9 ⁴ + 4 ⁴ + 7 ⁴ + 4 ⁴

由于1 = 1 ⁴不是总和，因此不包括在内。

这些数字的总和为1634 + 8208 + 9474 = 19316。

找到所有可以写为数字的五次幂之和的数字的总和。

11

强大的数字计数

问题63

5位数字16807 = 7 ⁵也是第五次幂。类似地，9位数字134217728 = 8 ⁹是九次幂。

存在多少个n位正整数，它们也是n次方？

12

13

吕克雷尔数

问题55

如果我们取47，则取反并加，即47 + 74 = 121，这是回文的。

并非所有数字都能如此迅速地产生回文。例如，

349 + 943 = 1292，

1292+ 2921 = 4213
       4213 + 3124 = 7337

也就是说，349进行了3次迭代才能得出回文。

尽管尚无人证明，但据认为有些数字（如196）从未产生过回文。从未通过反向和加法过程形成回文数的数字称为Lychrel数。由于这些数字的理论性质，并且出于此问题的目的，我们将假定一个数字为Lychrel，直到另行证明。此外，您得到的结果是，对于低于1万的每个数字，它要么（i）少于五十次迭代就成为回文，或者（ii）到目前为止，没有人拥有所有的计算能力将其映射到回文。实际上，10677是第一个在产生回文之前需要进行五十次迭代的数字：4668731596684224866951378664（53次迭代，28位数字）。

令人惊讶的是，回文数本身就是Lychrel数。第一个例子是4994。

一万以下有多少个Lychrel数？

注意：2007年4月24日，措词略有修改，以强调Lychrel数的理论性质。

14

计算至少四个不同质数小于100的数字

第268章

可以验证存在小于1000的23个正整数，这些整数可以被至少四个小于100的不同素数整除。

找出小于10 ^16的正整数可被至少四个小于100的素数整除。

15

关键平方和

第261章

让我们称之为正整数ķ一个正方形枢轴，如果有一对整数中号> 0且Ñ ≥ ķ，使得所述（总和米1）个连续的正方形高达ķ等于的总和米连续从（n +1）开始的平方：

（k - m）² + ... + k ² =（n +1）² + ... +（n + m）²。

一些小的方形枢轴是

• 4：3 ² + 4 ² = 5 ²

• 21：20 ² + 21 ² = 29 ²

• 24：21 ² + 22 ² + 23 ² + 24 ² = 25 ² + 26 ² + 27 ²

• 110：108 ² + 109 ² + 110 ² = 133 ² + 134 ²

找到所有的和独特的方形关键数据≤10 ¹⁰。

179. 最大数

.给定一组非负整数 nums，重新排列它们每个数字的顺序（每个数字不可拆分）使之组成一个最大的整数。

注意：输出结果可能非常大，所以你需要返回一个字符串而不是整数。

示例 1：

输入：nums = [10,2]

输出："210"

示例 2：

输入：nums = [3,30,34,5,9]

输出："9534330"

示例 3：

输入：nums = [1]

输出："1"

示例 4：

输入：nums = [10]

输出："10"

链接：https://leetcode-cn.com/problems/largest-number

152. 乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例 1:

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

202. 快乐数

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。

然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。

如果 可以变为  1，那么这个数就是快乐数。

如果 n 是快乐数就返回 true ；不是，则返回 false 。

示例 1：

输入：19

输出：true

解释：

12 + 92 = 82

82 + 22 = 68

62 + 82 = 100

12 + 02 + 02 = 1

示例 2：

输入：n = 2

输出：false

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/happy-number

289. 生命游戏

难度中等

根据 百度百科 ，生命游戏，简称为生命，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

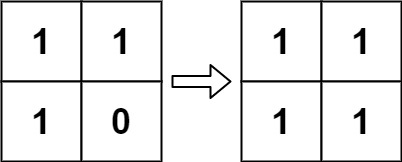
给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态：1 即为活细胞（live），或 0 即为死细胞（dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；

2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；

3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；

4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例 1：

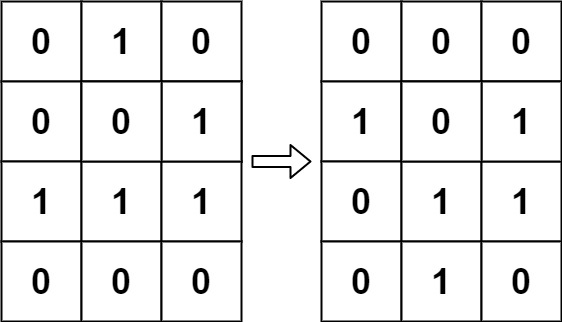
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]

提示：

• m == board.length

• n == board[i].length

• 1 <= m, n <= 25

• board[i][j] 为 0 或 1

进阶：

• 你可以使用原地算法解决本题吗？请注意，面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。

• 本题中，我们使用二维数组来表示面板。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题？

334. 递增的三元子序列

难度中等

给你一个整数数组 nums ，判断这个数组中是否存在长度为 3 的递增子序列。

如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ，使得 nums[i] < nums[j] < nums[k] ，返回 true ；否则，返回 false 。

 

示例 1：

输入：nums = [1,2,3,4,5]
输出：true
解释：任何 i < j < k 的三元组都满足题意

示例 2：

输入：nums = [5,4,3,2,1]
输出：false
解释：不存在满足题意的三元组

示例 3：

输入：nums = [2,1,5,0,4,6]
输出：true
解释：三元组 (3, 4, 5) 满足题意，因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6

 

提示：

• 1 <= nums.length <= 105

• -231 <= nums[i] <= 231 - 1

 

进阶：你能实现时间复杂度为 O(n) ，空间复杂度为 O(1) 的解决方案吗？

[编程题]寻找三角形

https://www.nowcoder.com/questionTerminal/c3f8d56fc9be4d55a36b0cf786c83ece?from=zhnkw

三维空间中有N个点，每个点可能是三种颜色的其中之一，三种颜色分别是红绿蓝，分别用'R', 'G', 'B'表示。
 现在要找出三个点，并组成一个三角形，使得这个三角形的面积最大。
 但是三角形必须满足：三个点的颜色要么全部相同，要么全部不同。

输入描述:

首先输入一个正整数N三维坐标系内的点的个数.(N <= 50) 

接下来N行，每一行输入 c x y z，c为'R', 'G', 'B' 的其中一个。x，y，z是该点的坐标。(坐标均是0到999之间的整数)

输出描述:

输出一个数表示最大的三角形面积，保留5位小数。

输入

5
R 0 0 0
R 0 4 0
R 0 0 3
G 92 14 7
G 12 16 8

输出

6.00000

超级素数幂

• https://www.nowcoder.com/questionTerminal/fb511c3f1ac447309368d7e5432c6c79?from=zhnkw
  

• 
  

如果一个数字能表示为p^q(^表示幂运算)且p为一个素数,q为大于1的正整数就称这个数叫做超级素数幂。现在给出一个正整数n,如果n是一个超级素数幂需要找出对应的p,q。

输入描述:

输入一个正整数n(2 ≤ n ≤ 10^18)

输出描述:

如果n是一个超级素数幂则输出p,q,以空格分隔,行末无空格。 如果n不是超级素数幂，则输出No

示例1

输入

27

输出

3 3

变换次数

https://www.nowcoder.com/questionTerminal/8c38063ca1574d93960c761f8f6efc81?from=zhnkw

牛牛想对一个数做若干次变换，直到这个数只剩下一位数字。
 变换的规则是：将这个数变成 所有位数上的数字的乘积。比如285经过一次变换后转化成2*8*5=80.
 问题是，要做多少次变换，使得这个数变成个位数。

输入描述:

输入一个整数。小于等于2,000,000,000。

输出描述:

输出一个整数，表示变换次数。

示例1

输入

285

输出

2

 LeetCode 第 279 号问题：完全平方数。

题目描述

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

输入: n = 12

输出: 3 

解释: 12 = 4 + 4 + 4.

输入: n = 13

输出: 2

解释: 13 = 4 + 9.

题目解析

这道题目很有意思。

大部分文章给出的答案都是依托于一个定理：四平方定理。

四平方定理讲的就是任何一个正整数都可以表示成不超过四个整数的平方之和。也就是说，这道题的答案只有 1，2 ，3，4 这四种可能。

同时，还有一个非常重要的推论满足四数平方和定理的数n（这里要满足由四个数构成，小于四个不行），必定满足 n = 4^a * (8b + 7)。

根据这个重要的推论来解决此题，首先将输入的n迅速缩小。然后再判断，这个缩小后的数是否可以通过两个平方数的和或一个平方数组成，不能的话我们返回3，能的话我们返回平方数的个数。

代码很简洁，如下：

% GDCP_ccl_20210530

%方法1：数学方法

clear
n=1472
y=0;

while rem(n,4)==0
    n=n/4;
end

if rem(n,8)==7
   y=4;
end

a=0;
while a*a<=n
      b=fix(sqrt(n-a^2));
      if a^2+b^2==n
         if (a~=0&b~=0)
            y=2;    
         else
            y=1;
         end
         break;
      end
      a=a+1;
end

if y~=1&y~=2&y~=4
   y=3;
end
y


         
%方法2：动态规划
%dp(i)的值表示数字i对应的完全平方数的个数。

clear
n=26;
dp(1:n)=ones(1,n)*10000;  %初始化数组dp()，设为非常大的数
dp(1)=1;  %初始化前3个元素
dp(2)=2;
dp(3)=3;

for k=2:fix(sqrt(n))  %把n之内符合平方数原则的，赋值为1
     dp(k^2)=1;
end

for i=2:fix(sqrt(n-1))   %
    for j=i^2+1:n        %dp(j)从第5个开始算起  
        dp(j)=min( dp(j) , dp(j-i^2)+1  ); %动态规划递推公式
    end
end
dp

我们要知道12最少有多少个数构成，实际上如果我们走了一步的话，我们需要知道11、8、3对应的步数，如果我们不走，我们就需要知道12的步数，我们只要通过比较是走0步小，还是走1步哪个更小即可。通过一个式子表示就是

num[n] = min(num[n], num[n-i**2] + 1)

所以我们可以先定义一个n大小的数组（static类型），这里我们要使数组初始化为无穷大，在python中我们可以使用float('inf')

class Solution:

    _dp = list()

    def numSquares(self, n):

        """

        :type n: int

        :rtype: int

        """

        dp = self._dp

        dp = [float('inf') for i in range(n + 1)]

        dp[0] = 0

        for i in range(n + 1):

            j = 1

            while i + j**2 <= n:

                dp[i + j**2] = min(dp[i + j**2], dp[i] + 1)

                j += 1

                

        return dp[n]

 这道题目其实是有很多种的解法，最容易想到的是使用递归来搜索所有可能的组合方案，在所有搜索到的方案中找到组成当前数字n的最少的平方个数。此外分析题目比较容易想到另外一种是完全背包模型，我们可以将n看成是背包的容量v，平方数字看成是每一种物品的体积，每种物品的价值为1，对于这道题目来说我们需要求解构成n的最少的平方数字的数目，所以dp的含义会发生变化，这里dp[j]的含义是当前体积为j使用的最少的平方数的数目，根据dp的含义进行递推即可，最终dp[n]就是我们要求解的答案，不过提交上去运行需要几秒。

import math

class Solution:

    def numSquares(self, n: int) -> int:

        dp = [100000] * (n + 2)

        dp[0] = 0

        s = int(math.sqrt(n))

        vi = [0]

        for i in range(1, s + 1):

            vi.append(i * i)

        for i in range(1, s + 1):

            for j in range(vi[i], n + 1):

                # 当前背包容量为j而且使用当前物品vi[i]的最少平方数字的数目

                dp[j] = min(dp[j], dp[j - vi[i]] + 1)

        return dp[n]

动规解法：对一个数字n而言，组成的它的完全平方数的最少个数可以根据它减去i*i（这里i*i<n）后对应的那个数的最少完全平方数加一，通过改变i的值最终取得最小值。

还是从简单情况开始

1   1>=1*1 所以1对应等于0对应的最小个数加1,这里0对应的个数为0

2   2>=1*1 所以2对应等于1对应的最小个个数加1，因为之前已经记录了1对应的最小值为1，所以这里最小为2

3   3>=1*1 所以3对应等于2对应的最小个个数加1，因为之前已经记录了2对应的最小值为1，所以这里最小为3

4   4>=1*1和4>=4 所以4对应等于3或者0对应的最小个个数加1，因为之前已经记录了3对应的最小值为3，0对应的最小值为0，所以最终的最小值为1。

往后的情况依次类推。。。

广度优先搜索

建立一个队列，用于广度优先搜索，广度优先搜索是层层推进的，当到某层符合条件了，就break，返回ans；注意，这里不能用深度优先搜索，大家思考下为什么。

四平方数定理

这个问题本身是存在数值解的。大家可以搜索下"四平方数定理"，所有我在循环设置了超过4层就退出的条件，提升算法效率

候选数用数组缓存起来

var numSquares = function(n) {

        //4平方数定律，最大的返回值不超过4，而且先把候选数用数组缓存起来

        let ans = 4;

        const squared = [10000,9801,9604,9409,9216,9025,8836,8649,8464,8281,8100,7921,7744,7569,7396,7225,7056,6889,6724,6561,6400,6241,6084,5929,5776,5625,5476,5329,5184,5041,4900,4761,4624,4489,4356,4225,4096,3969,3844,3721,3600,3481,3364,3249,3136,3025,2916,2809,2704,2601,2500,2401,2304,2209,2116,2025,1936,1849,1764,1681,1600,1521,1444,1369,1296,1225,1156,1089,1024,961,900,841,784,729,676,625,576,529,484,441,400,361,324,289,256,225,196,169,144,121,100,81,64,49,36,25,16,9,4,1];

        //建立一个队列，用于广度优先搜索，广度优先搜索是层层推进的，当到某层符合条件了，就break，返回ans

        const q = [];

        q.push(n);

        let level= 0;

        while (q.length > 0) {

            const size = q.length;

            level++;

            if (level >= 4) break;

            for (let i=0; i<size; i++) {

                const item = q.shift();

                //console.log('q=%o size=%o item=%o level=%o', q, size, item, level);

                if (squared.includes(item)) {

                    return level;

                } else {

                    for (let i=squared.length-1; i>=0; i--) {

                        if (squared[i] < item) q.push(item - squared[i]);

                        else break;

                    }

                }

            }

        }

        return ans;

};

约瑟夫环问题。

我的代码：20210405

%%  约瑟夫环

clear clc

s=1:33   %生成原始环

k=7;       %间隔数

while  length(s)>1

      if  length(s)>k-1 

          s( length(s)+1 : length(s)+k-1 ) = s( 1 : k-1 );

          s( 1 : k ) = [];

          s

      else

           if    mod( k , length(s) )==0

                 s(end)=[];

                 s

            else 

                 s( mod( k , length(s) ) )=[];

                 s

            end

      end

end      

方法2：递归调用。。

有 个人围成一个圈，每 个人踢掉一个人，问最后留下来的人是几号？

是不是很熟悉？当初你们刚学的时候怎么做的？是不是用链表？是不是写得痛不欲生，还超时了？哦不是那算了。

如果用链表暴力求解的话，时间复杂度是 ，但是用我下面的方法，可以加速到 。

下面我讲一个具体数学课上讲到的简洁解法：

假设初始编号为 ，现在考虑一种新的编号方式。

第一个人不会被踢掉，那么他的编号从 开始往后加 1 ，变成 ，然后第二个人编号变为 ，直到第 个人，他被踢掉了。

然后第 个人编号继续加 1 ，变成了 ，依次下去。

考虑当前踢到的人编号为 ，那么此时已经踢掉了 个人，所以接下去的人新的编号为 。

所以编号为 的人编号变成了 ，其中 。

直到最后，可以发现活下来的人编号为 ，问题是怎么根据这个编号推出他原来的编号？

以 为例，下图就是每个人新的编号：

令 ，那么他上一次的编号是

因为

所以上一次编号可以写为

因此最后存活的人编号可以用如下的算法计算：

N = qn
while N > n:
    N = k + N - n
ans = N

其中 。

如果我们用 替代 ，将会进一步简化算法：

算法伪代码如下：

D = 1
while D <= (q-1)n:
    D = k
ans = qn + 1 - D

其中 。

最后用这个算法来求解一道经典约瑟夫环题目，题目链接：

Problem - 3089acm.hdu.edu.cn

注意到这题 的范围高达 ，不管用 的暴力还是 的递归都会原地爆炸boom boom boom~ 这时候就得动用上面的方法了。

C++代码如下：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

LL Ceil(LL x, LL y) {
    return x / y + (x % y != 0);
}

LL J(LL n, LL q) {
    LL D = 1, end = (q - 1) * n;
    while (D <= end) {
        D = Ceil(q * D, q - 1);
    }
    return q * n + 1 - D;
}

int main() {
    LL n, q;
    while (~scanf("%lld%lld", &n, &q)) {
        printf("%lld\n", J(n, q));
    }
    return 0;
}

约瑟夫环

问题： N个人编号为1，2，……，N，围成一个环，依次报数，每报到M时，杀掉那个人，求最后胜利者的编号。

换一下编号，现在假设有10个人编号为a,b,c,d,e,f,g,h,i,j，M=3吧。

杀第一个人的结果如下

杀第二个人的时候相当于从d开始，结果如下

最后我们可以知道d最终存活了下来,设f(n) = x 表示有n个人时存活下来的是x,这里f(10)=d。

现在我们来跟踪一下d的位置变化

一开始杀第一个人时d的位置

然后杀第二个人时d的位置

看到这里我想你应该什么都看不出来，如果我此时问你如果只有9个人那么那个人存活的下标是多少你应该也是看不出来的。

这里不是说大家笨，大家都是这样子，一开始谁能反映的过来的啊。不用急听我细细道来。

在看一下这个图

我们很容易就可以得知最后一个是一个死人，死人是不会再被数一次的，那我们就吧最后一个死人删掉吧。

那此时不就相当于只有9个人的情况吗

虽然字母顺序对不上，但是如果只看下标的话你应该能够说出9个人的时候下标是多少的人存活下来吧也就是下标为0。

而且这个下标不是随便来的，而是按照一定的规律出现的，也就是f(9) = f(10) - M,可能有人会问如果下标越界了咋办啊。那还不简单取模不就可以了。f(n)有可能会是负数，负数取模可能比较抽象，那我们转换成正数取模吧(这一步是比较顺理成章的希望没有把你困扰住） 也就是 f(10) = f(9)+M ， 为了预防越界也就是f(10) = (f(9)+M) %10; 为什么是和10取模而不是和9取模呢？这一点的是因为9个人时是由10个人通过移位再去掉最后一个死人后得到的本质上还是10个人，自然就是要和10取模，也可以通过上面的图，更好的理解这一点。

通过这个例子，想必你能够简单的写出递归式子了吧，也就是f(n) = (f(n-1)+M)%n。

全过程如下：

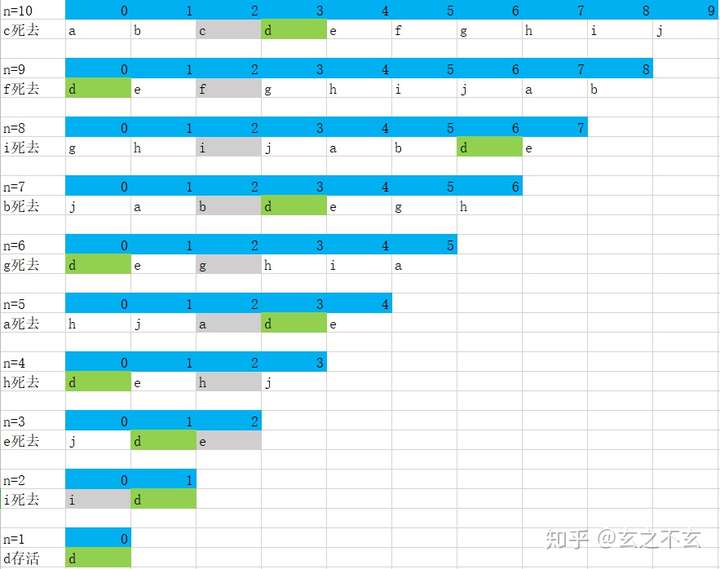
代码很简单

public int f(int n,int m){
        if(n==1) return 0;
        return (f(n-1,m)+m)%n;
    }

当然这题还有其他解法，数组法和链表法，这些思维量就少一些了。

问题描述

约瑟夫环问题是这样的：

0, 1, …, n - 1 这 n 个数字排成一个圆圈，从数字 0 开始，每次从这个圆圈里删除第 m 个数字。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4 这 5 个数字组成一个圆圈，从数字 0 开始每次删除第 3 个数字，则删除的前 4 个数字依次是 2、0、4、1，因此最后剩下的数字是 3。如下图所示。

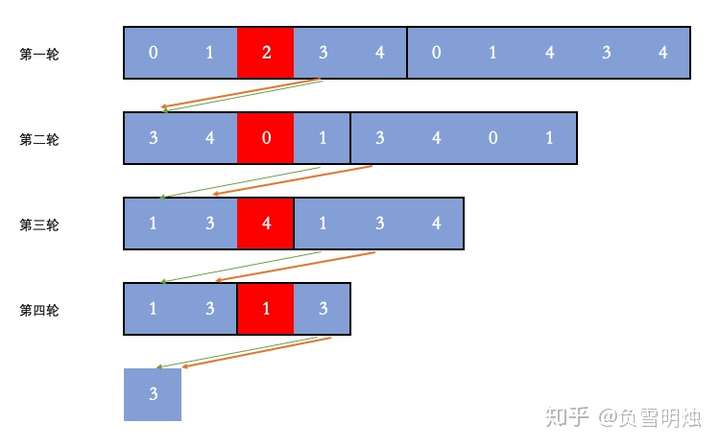
解法

解决约瑟夫环问题，我们采用倒推，我们倒推出：最后剩下的这个数字，在最开始的数组中的位置。

1. 剩下最后一个数字（简称“它”）的时候，总个数为 1，它的位置 pos = 0。

2. 那么它在上一轮也是安全的，总个数为 2，它的位置 pos = (0 + m) % 2；

3. 那么它在上上轮也是安全的，总个数为 3，它的位置 pos = ((0 + m) % 2 + m) % 3；

4. 那么它在上上上轮也是安全的，总个数为 4，它的位置 pos = (((0 + m) % 2 + m) % 3) % 4；

5. ...

6. 那么它在游戏开始的第一轮也是安全的，总个数为 n，它的位置 pos 就是最后的结果。

即如果从下向上反推的时候：假如它前一轮的索引为 pos，那么当前轮次的位置就是 (pos + m) % 当前轮次的人数。

最后，由于给出的数字是 nums = 0, 1, 2, .., n - 1，即 nums[i] = i，因此找出 pos 就相当于找到这个数字。

大部分解法解到这里就结束了，缺乏递推公式的数学证明，现就数学推导说明如下。

数学推导

定义：

1. 约瑟夫环操作：把一些数字排成一个圆圈，从数字 0 开始，每次从这个圆圈里删除第 m 个数字，直到最后只剩一个数字。

2. 函数 f(n, m) ：表示对 n 个数字 0, 1, …, n - 1 做约瑟夫环操作，最后剩下的这个数字。（这个定义特别重要，理解之后才向下看）

下面开始推导。

整体思路：
在以 0 为起始的长度为 n 的序列上做约瑟夫环操作的最终结果 f(n, m) =
在完成上轮操作删除数字 k 之后的新序列上的约瑟夫环操作的最终结果 h(n - 1, m) =
将新序列映射成以 0 为起始的长度为 n - 1 的序列上的约瑟夫环操作的最终结果 f(n - 1, m) 的逆映射。

1. 得到下次操作的新序列

在 0, 1, …, n - 1 这 n 个数字中，第一个被删除的数字是 (m - 1) % n。为了简单起见，我们把 (m - 1) % n 记为 k，那么删除 k 之后剩下的 n - 1 个数字为 0, 1, …, k - 1, k + 1, …, n - 1，并且下一次删除时要从 k + 1 开始计数。相当于在剩下的序列中， k + 1 排在最前面，所以第二次操作的序列是 k + 1, …, n - 1, 0, 1, …, k - 1。

2. 得到新序列上函数

在这个新序列上再完成约瑟夫环操作，最后剩下的数字应该是关于 n 和 m 的函数，即也可以用 f(n, m) 进行表示。但由于现在的这个序列的排列（从 k + 1 开始）和最初的序列（从 0 开始）不一样，因此这个时候的函数已经不同于最初的函数，记为 h(n - 1, m)，此函数的定义：在 k + 1, …, n - 1, 0, 1, …, k - 1 这 n - 1个数字的序列上做约瑟夫环操作，最后剩下的这个数字。

3. 求解新函数

由于 在最初序列上 和 在新序列上 完成约瑟夫操作剩下的数字均为同一个数字，所以有 f(n, m) = h(n - 1, m)。（新序列是从最初序列转化的，会最终转化到同一个数字）

下面的工作就是求解新函数 h(n - 1, m) ，使其能够用 f(n - 1, m) 表示出来。

由于 f(n - 1, m) 是定义在以 0 为开始的序列上的，所以我们把剩下的这 n - 1 个数字的序列 k + 1, …, n - 1, 0, 1, …, k - 1 进行映射，映射到结果是形成一个 0 ~ n - 2 的序列。

 k + 1 → 0

 k + 2→ 1

...

 n - 1 → n - k -2

 0 → n - k - 1

 1 → n - k

...

 k - 1 → n - 2

该映射函数是个一元一次函数，定义为 p(x)，则 p(x) = (x + n - k - 1) % n。（还记得初中的 y = x + a 怎么求么？如果不懂见附录1）

从左到右的映射是 p(x)，从右到左的映射叫做逆映射 p-1(x) = (x + k + 1) % n。（该逆映射的求法见本章结尾附录2）

由于映射之后的序列和最初的序列有同样的形式，即都是从 0 开始的连续序列，因此在映射之后的序列上做约瑟夫环操作的结果仍可以用函数 f 表示，记为 f(n - 1, m)。

在映射之前的序列上的约瑟夫环操作的结果是 h(n - 1, m)，在映射之后的序列上的约瑟夫环操作的结果是 f(n - 1, m)，则 f(n - 1, m) = p( h(n - 1, m) )。

所以有：

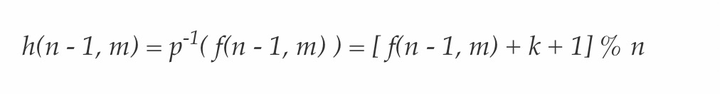
把 k = (m - 1) % n 代入得到：（k 中有取余运算，为什么代入之后没有了？见本章结尾附录3）

 f(n, m) = h(n - 1, m) = [ f(n - 1, m) + m ] % n

终于，经过复杂的分析，我们找到了一个只包含有 f 函数的递推公式。要得到 n 个数字的序列中完成约瑟夫环操作最后剩下的数字，只需要得到 n - 1 个数字的序列中最后剩下的数字，并以此类推。（像不像递归？）

当 n = 1 时，也就是序列中只有 1 个数字 0，那么完成约瑟夫操作最后剩下的数字就是0。（像不像递归终止条件？）

我们把这种关系表示为：

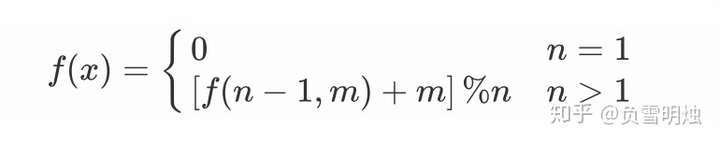
这个公式无论是递归还是循环都很好实现。

附录1. p(x)的推导

看到这里的同学肯定好奇公式中的%号是怎么得到的，其实是个分段函数归纳的。

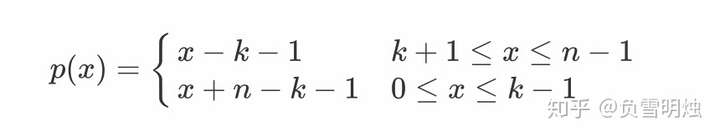
所以，为了把分段函数统一，使用 p(x) = (x + n - k - 1) % n。

附录2. p-1(x)的推导

已知p(x) = (x + n - k - 1) % n，求 p-1(x)。

p(x) = (x + n - k - 1) % n = (x + n - k - 1) + (T - 1)n = x - k - 1 + Tn

其中引入的正整数 T 的取值方法：取合适的 T 以保证0 <= p(x) <= n。（这一步不懂的可以用p(0) = n - k -1代入，此时 x = 0, T = 1）

可以得到x = p(x) + k + 1 - Tn，逆函数就是把 x 替换成 p(x)，把 p(x) 替换成 x。

所以逆函数 p-1(x) = x + k + 1 - Tn = (x + k + 1) % n。

附录3. 消除括号里的模运算

模运算的四则规则：(a + b) % p = (a % p + b % p) % p，选自百度百科。

证明 [ f(n - 1, m) + (m - 1) % n + 1] % n = [ f(n - 1, m) + m ] % n .

左边 = [ f(n - 1, m) + (m - 1) % n + 1] % n

= [ (f(n - 1, m) + 1) % n + (m - 1) % n] % n ，由于0 < 映射后的取值 f(n - 1, m) < n - 2，所以1 < f(n - 1, m) + 1< n - 1，所以可以添加第一个取余运算。

= [ (f(n - 1, m) + 1) + (m - 1) ] % n ，运用四则运算公式

= [ f(n - 1, m) + m ] % n

= 右边

得证。

代码

pos = 0 开始，代表了最后结果只剩下了 1 个数字，这个数字处于第 0 个位置。

循环从数组长度有 2 个开始，即从剩下了两个数字开始计算。

循环到数组中剩下 n 个人结束，即到达了题目要求的那么多数字，此时的 pos 就是最后剩下的那个数字的在 n 个数字中位置。

Python 代码如下：

class Solution:
    def lastRemaining(self, n: int, m: int) -> int:
        pos = 0
        for i in range(2, n + 1):
            pos = (pos + m) % i
        return pos

*注：本数学推导基于《剑指Offer》中的推导进行了更详细的讲解。

参考文献：

1. 《剑指Offer》

2. 力扣（LeetCode）链接：https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof

3. https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/javajie-jue-yue-se-fu-huan-wen-ti-gao-su-ni-wei-sh/

===================================

===================================

1、输入一个非负整数 n，请你计算阶乘 n! 的结果末尾有几个 0。

比如说输入 n = 5，算法返回 1，因为 5! = 120，末尾有一个 0。

函数签名如下：

int trailingZeroes(int n);

2、输入一个非负整数 K，请你计算有多少个 n，满足 n! 的结果末尾恰好有 K 个 0。

比如说输入 K = 1，算法返回 5，因为 5!,6!,7!,8!,9! 这 5 个阶乘的结果最后只有一个 0，即有 5 个 n 满足条件。

函数签名如下：

int preimageSizeFZF(int K);

我把这两个题放在一起，肯定是因为它们有共性，下面我们来逐一分析。

题目一

肯定不可能真去把 n! 的结果算出来，阶乘增长可是比指数增长都恐怖，趁早死了这条心吧。

那么，结果的末尾的 0 从哪里来的？我们有没有投机取巧的方法计算出来？

首先，两个数相乘结果末尾有 0，一定是因为两个数中有因子 2 和 5，因为 10 = 2 x 5。

也就是说，问题转化为：n! 最多可以分解出多少个因子 2 和 5？

比如说 n = 25，那么 25! 最多可以分解出几个 2 和 5 相乘？这个主要取决于能分解出几个因子 5，因为每个偶数都能分解出因子 2，因子 2 肯定比因子 5 多得多。

25! 中 5 可以提供一个，10 可以提供一个，15 可以提供一个，20 可以提供一个，25 可以提供两个，总共有 6 个因子 5，所以 25! 的结果末尾就有 6 个 0。

PS：我认真写了 100 多篇原创，手把手刷 200 道力扣题目，全部发布在 labuladong的算法小抄，持续更新。建议收藏，按照我的文章顺序刷题，掌握各种算法套路后投再入题海就如鱼得水了。

现在，问题转化为：n! 最多可以分解出多少个因子 5？

难点在于像 25，50，125 这样的数，可以提供不止一个因子 5，怎么才能不漏掉呢？

这样，我们假设 n = 125，来算一算 125! 的结果末尾有几个 0：

首先，125 / 5 = 25，这一步就是计算有多少个像 5，15，20，25 这些 5 的倍数，它们一定可以提供一个因子 5。

但是，这些足够吗？刚才说了，像 25，50，75 这些 25 的倍数，可以提供两个因子 5，那么我们再计算出 125! 中有 125 / 25 = 5 个 25 的倍数，它们每人可以额外再提供一个因子 5。

够了吗？我们发现 125 = 5 x 5 x 5，像 125，250 这些 125 的倍数，可以提供 3 个因子 5，那么我们还得再计算出 125! 中有 125 / 125 = 1 个 125 的倍数，它还可以额外再提供一个因子 5。

这下应该够了，125! 最多可以分解出 20 + 5 + 1 = 31 个因子 5，也就是说阶乘结果的末尾有 31 个 0。

理解了这个思路，就可以理解解法代码了：

int trailingZeroes(int n) {
    int res = 0;
    long divisor = 5;
    while (divisor <= n) {
        res += n / divisor;
        divisor *= 5;
    }
    return res;
}

这里 divisor 变量使用 long 型，因为假如 n 比较大，考虑 while 循环的结束条件，divisor 可能出现整型溢出。

上述代码可以改写地更简单一些：

int trailingZeroes(int n) {
    int res = 0;
    for (int d = n; d / 5 > 0; d = d / 5) {
        res += d / 5;
    }
    return res;
}

这样，这道题就解决了，时间复杂度是底数为 5 的对数，也就是 O(logN)，我们看看下如何基于这道题的解法完成下一道题目。

===================================

以下题目来自：https://www.lintcode.com/

最大点的集合

中等

给定一个坐标点列表 Points，其中Points 中 Point[i][0] 表示横轴坐标，Points[i][1] 表示纵轴坐标。
当存在点 p 满足 Points 中任意点都不在 p 的右上方区域内（横纵坐标都大于p），则称其为最大点。
返回所有最大点，列表中的最大点按照 X 轴从小到大的方式排序。

• Points 点集中点的个数范围是: [1, 500000]

• points[i][0] 和 points[i][1]的范围是: [0, 10^9]

• 保证横坐标和纵坐标都不重复

样例

示例 1:
输入:
Points = [[1, 2], [5, 3], [4, 6], [7, 5], [9, 0]]
输出: [[4, 6], [7, 5], [9, 0]]
解释: 不存在其他点的横纵坐标都大于点[4, 6], [7, 5], [9, 0]

示例 2:
输入:
Points = [[9,10],[7,8],[8,9],[1,1],[5,2]]
输出: [[9, 10]]
解释: 不存在其他点的横纵坐标都大于点[9, 10]


首先对于所有的点进行x坐标从大到小排序。 
然后用一个变量 max_y 来存储目前最大的y。 
当你遍历这个排好序的数组的时候，只要该点的 y 大于 max_y 就证明是最大点。
/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param Points: a list of [x, y]
    @return: return a list of points
    """
    def MaximumPointsSet(self, Points):
        # write your code here
        n, max_y = len(Points), -1
        vis, result = [0] * n, []

        nums = sorted(Points, key=lambda x: -x[0])
        
        for i in range(n):
            if nums[i][1] > max_y:
                vis[i] = 1
            max_y = max(nums[i][1], max_y)
        
        for i in range(n - 1, -1, -1):
            if vis[i] == 1:
                result.append([nums[i][0], nums[i][1]])
        
        return result

 最小分解

中等

给定一个正整数a，找到最小的正整数b，它的每个数字相乘之后等于a。

如果没有答案，或者答案超过了32位有符号整型的范围，返回0。

样例

样例 1:

输入: 48
输出: 68

样例 2:

输入: 15
输出: 35

用 2-9 对 a 因数分解, 如果无法分解说明无解, 比如说 a = 11.

为了使 b 尽可能小, 所以我们首选尽可能大的数字来分解 a, 即从9到2依次尝试, 尽可能多地提取每一个数字.

然后将分解的因数从小到大排列就可以组成答案 b, 在返回之前, 需要检查是否溢出/超过int范围.

以上算法中蕴含贪心的思想.

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

# python3
class Solution:
    """
    @param a: a positive integer
    @return: the smallest positive integer whose multiplication of each digit equals to a
    """
    def smallestFactorization(self, a):
        res = ''
        for i in range(9, 1, -1):
            while a % i == 0:
                res = str(i) + res
                a //= i
        if a != 1:
            return 0
        res = int(res) 
        if res > 0x7fffffff:
            return 0
        else:
            return res

等差切片

中等

如果一个数字序列由至少三个元素组成并且任何两个连续元素之间的差值相同，则称为等差数列。

举个例子，这些是等差数列：

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

下面的序列不是等差数列：

1, 1, 2, 5, 7

给一个由 N 个数组成且下标从 0 开始的数组A。这个数组的一个切片是指任意一个整数对 (P, Q) 且满足 0 <= P < Q < N。

如果 A 中的一个切片(P, Q) 是等差切片，则需要满足A[P], A[p + 1], ..., A[Q - 1], A[Q] 是等差的。还需要注意的是，这也意味着 P + 1 < Q。

需要实现的函数应该返回数组 A 中等差切片的数量。

样例

样例1

输入： [1, 2, 3, 4]
输出： 3
解释：
 A 中的 3 个等差切片为: [1, 2, 3], [2, 3, 4] 以及 [1, 2, 3, 4].

样例2

输入： [1, 2, 3]
输出： 1

不妨设dpi表示以ai结尾的最长的等差数列长度。 转移方程为： $dpi=dpi-1+1 \quad if(ai-ai-1==ai-1-ai-2)$ $dpi=2 \quad if(ai-ai-1!=ai-1-ai-2)$ 最后的答案为$\sum_{i=0}^{n}dpi-2 \quad if(dpi>2)$

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param A: an array
    @return: the number of arithmetic slices in the array A.
    """

    def numberOfArithmeticSlices(self, A: list)->int:
        # Write your code here
        size = len(A)
        if size in (0, 1, 2):
            return 0

        t = [A[i] - A[i - 1] for i in range(1, len(A))]
        dp = [0 for i in range(size)]
        for i in range(2, size):
            if t[i-2] == t[i - 1]:
                dp[i] = dp[i - 1] + 1
            else:
                dp[i] = 0

        return sum(dp)

有效的括号字符串

中等

给定一个只包含三种类型字符的字符串：'（'，'）'和 '*'， 编写一个函数来检查该字符串是否有效。 我们通过以下规则定义字符串的有效性：

1.任何左括号 '('必须有一个相应的右括号')'。
2.任何右括号 ')' 必须有一个相应的左括号'('。
3.左括号'(' 必须在相应的右括号 ')' 之前。
4.*可以被视为单个右括号'）'或单个左括号'（'或空字符串。
5.空字符串也有效。

1. 字符串的长度范围为 [1, 100]。

样例

样例 1:
	输入:  "()"
	输出:  true

	
样例 2:
	输入: "(*)"
	输出:  true
	
	解释:
	'*' 看作是空串.
	
样例 3:
	输入: "(*))"
	输出: true
	
	解释:
	'*' 当作'('

dfs with memorization, maybe more straightforward in thinking

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

def checkValidString(self, s):
        if s == '':
            return True
        
        memo = {}
        return self.dfs(0, 0, s, memo)
    
    def dfs(self, index, leftDegree, s, memo):
        if (index, leftDegree) in memo:
            return memo[(index, leftDegree)]
        
        result = False 
        
        if index == len(s):
            if leftDegree == 0:
                return True 
            else:
                return False
            
        # leftDegree could never be less than 0
        if leftDegree < 0:
            result = False 
        else:
            if s[index] == '(':
                if self.dfs(index + 1, leftDegree + 1, s, memo):
                    result = True
            elif s[index] == ')':
                if self.dfs(index + 1, leftDegree - 1, s, memo):
                    result = True 
            else:
                if self.dfs(index + 1, leftDegree, s, memo):
                    result = True 
                if self.dfs(index + 1, leftDegree + 1, s, memo):
                    result = True
                if self.dfs(index + 1, leftDegree - 1, s, memo):
                    result = True
        
        memo[(index, leftDegree)] = result
        return result

一道简单的思维题，考虑到星号在其中的用处就能解决. 1. 首先进行最基础的考虑，（在不考虑星号的情况下）我们必定会选择位置最接近的左右括号配对，这样避免了人为造成的右括号前面没有左括号匹配的惨剧。因此我们在写程序进行处理的时候，对于每个右括号判断前面是否有1个左括号能被他拥有，如果左括号数量不足，这个字符串必定是false，或者当整个串被匹配完之后发现有多余的左括号，这个字符串同样是false

2. 接下来考虑有星号的情况:”)”必须由位置在它之前的”(”或”*”匹配，如果”(”或者”*”数量不足导致的false是无法避免的，而如果”(“ 比”)”多，将”(”与”*”优先匹配可以减小false的可能性。举个例子如样例3，从左往右遍历的时候，优先匹配”(”和”*”，遇见第一个”)”，发现没有单独的”(”,从”(*”的组合中拆出一个”(“与之匹配，而原先匹配中的*因为可以等同于不存在便不予理会，接着遇到第二个”)”,拿走刚才剩余的”*”。综上我们可以观察到，”(”容易受制于”)”而将其与”*”匹配后就很灵活，不仅避免了数量太多带来的麻烦，也能在和*匹配后再次提供自身给”)”进行匹配。而如果这样匹配结束还有多余的”(”则必定false

3. 我们设l（left）为必须被右括号匹配的左括号数量，cp（couple）为前面左括号和星号数量。遍历字符串，遇到左括号和星号的时候,cp++; 遇到右括号的时候cp--; 遇到星号，默认先于前面的左括号(l>0)匹配,此时(l—)，遇到右括号，默认先与前面必须与右括号匹配的左括号匹配，此时(l—;cp—;)或者在支援兵中考虑(cp—) 注意cp是前方左右的左括号和星号数量，一旦cp<0即false. 匹配完发现(l>0)即多出了左括号，也为false。剩下的情况就是true了

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param s: the given string
    @return: whether this string is valid
    """
    def checkValidString(self, s):
        # Write your code here
        n = len(s)
        left, cp = 0, 0
        for i in range(0, n):
            if s[i] == '(':
                left += 1
                cp += 1
            elif s[i] == '*':
                if left > 0:
                    left -= 1
                cp += 1
            else:
                if left > 0:
                    left -= 1
                cp -= 1
                if cp < 0:
                    return False
        
        if left > 0:
            return False
        else:
            return True

组合新数字

中等

现在有一个数组a，你可以从里面取任意个数字，用这些数字组成一个新的数字，例如5，12，3三个数字可以组成新数字5123。
题目需要你求出最大的能被3整除的新组合数字。

1. 0< |a| <1000

2. 0<= a[i] <=1000 (0<= i < |a|)

3. 题目保证数据一定有解

样例

样例1：

输入：[1,2,2]
输出："21"

样例2：

输入：[1,2,4,6]
输出："642"

样例3：

输入：[3,0,6,9]
输出："9630"

这题分两步走： 1. 去掉1个或者2个数字，令余下的数字加起来是3的倍数 （类似Leetcode 1363. Largest Multiple of Three） 2. 把剩下的数组合起来，令这个数字越大越好 （类似LeetCode 179 Largest Number）

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

from functools import cmp_to_key
class Solution:
    def Combine(self, a):
        tot = 0
        cnt = [[] for i in range(2)]
        a.sort()
        for i in range(len(a)):
            n = a[i]
            tot = tot + n
            if n % 3 == 1 and len(cnt[0]) <= 2:
                cnt[0].append(i)
            if n % 3 == 2 and len(cnt[1]) <= 2:
                cnt[1].append(i)
                
        RmIdx = []
        if tot % 3 == 1:
            if len(cnt[0]) >= 1:
                RmIdx = [cnt[0][0]]
            else:
                RmIdx = cnt[1]
        
        if tot % 3 == 2:
            if len(cnt[1]) >= 1:
                RmIdx = [cnt[1][0]]
            else:
                RmIdx = cnt[0]
                
        a = [str(a[i]) for i in range(len(a)) if i not in RmIdx]
        a.sort(reverse=True, key=cmp_to_key(lambda x, y: -1 if x + y < y + x else 1))
        return ''.join(a)

排除法+字典排序法

首先， 我们要组合最大的数字分2个步骤， 一个是从list里面挑尽可能多的数出来。 digits越多， 数越大嘛。 另一个是， 这些数要从大到小排。 遇到2位数跟1位数去比的， 咱们就看看他们用str加一起哪个大。

然后我们就要看选数的时候， 怎么选。 我们发现整除3其实就是每个位置上加起来等于3. 那么如果加起来直接整除3的， 就说明都要。 如果mod 3余1， 那说明淘汰个最小的余1的就行。 如果余2， 那么淘汰2个余1， or 1个余2即可。 有的人可能想不通， 为什么不直接淘汰余2的。 有个test case， 比如说最小的几个数是 1， 1， 23这个时候肯定淘汰2个1

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

import functools

class Solution:
    """
    @param a: the array in problem.
    @return: represent the new number.
    """
    def Combine(self, A):
        sum_a = sum(A)
        if sum_a % 3 == 0:
            return self.largest_num_from_list(A)

        sorted_a = sorted(A)
        if sum_a % 3 == 1:
            index_1 = self.smallest_k_from_index(sorted_a, 1, 0)
            sorted_a.pop(index_1)
        else:
            index_1a = self.smallest_k_from_index(sorted_a, 1, 0)
            index_1b = self.smallest_k_from_index(sorted_a, 1, index_1a + 1)
            index_2 = self.smallest_k_from_index(sorted_a, 2, 0)
            if not index_1a or not index_1b or (sorted_a[index_2] < int(str(index_1a) + str(index_1b)) or sorted_a[index_2] < int(str(index_1b) + str(index_1a))):
                sorted_a.pop(index_2)
            else:
                sorted_a.pop(index_1b)
                sorted_a.pop(index_1a)
        return self.largest_num_from_list(sorted_a)

    def smallest_k_from_index(self, A, K, index):
        for i in range(index, len(A)):
            if A[i] % 3 == K:
                return i

    def largest_num_from_list(self, A):
        A.sort(key = functools.cmp_to_key(self.cmp))
        return "".join([str(num) for num in A])

    def cmp(self, a, b):
        return 1 if str(a) + str(b) < str(b) + str(a) else -1

解题思路：

按照题意的思路去考虑取哪些数，这样情况会比较复杂，解题费时。可以考虑不取哪些数。 可以想到，当数组和模三余0时，必定全取； 当数组和模三余1时，不取一个模三余1的数，或者不取两个模三余2的数； 当数组和模三余2时，不取一个模三余2的数，或者不取两个模三余1的数。

算法流程：

• 列表项目计算数组和模三的余数sum，将数组按数值从小到大排序并遍历，第一个模三余数等于sum的数不取，其他数均取

• 将数组内所有值进行排序得到最大值字符串ans_1（自定义排序，比较数字a和b不同顺序连接得到的两个字符串ab和ba大小决定其排序）

• 将数组按数值从小到大遍历，第一个和第二个模三余数等于（3-sum）的数不取，其他数均取，同上得到ans_2

• 若ans_2均存在，返回max(ans_1，ans_2)，否则返回ans_1

复杂度分析：

• 时间复杂度：O(nmlogn) n为数组长度，m为数组中数字位数，因为排序时复杂度为nlogn，且在其基础上定义了字符串比较大小

• 空间复杂度：O(nm) 需要存下将数组中数组转化为字符串的所有字符

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param a: the array in problem.
    @return: represent the new number.
    """
    # 自定义排序函数
    def c(self, x, y):
        if x + y > y + x:
            return -1
        return 1
    
    def Combine(self, a):
        tmp_1 = []
        tmp_2 = []
        ans_1 = ""
        ans_2 = ""
        flag = 0
        # 求数组和模三的余数sum
        mod = sum(a) % 3
        a.sort()
        for i, v in enumerate(a):
            if flag == 0 and v % 3 == mod and mod != 0:
                # 第一个模三余数等于sum的数不取
                flag = 1
            else:
                tmp_1 += [str(v)]
        tmp_1 = sorted(tmp_1,self.c)
        for i,v in enumerate(tmp_1):
            ans_1 += v
        flag = 0;
        for i, v in enumerate(a):
            if flag < 2 and v % 3 == 3 - mod:
                # 第一个和第二个模三余数等于3 - sum的数不取
                flag += 1
            else:
                tmp_2 += [str(v)]
        tmp_2 = sorted(tmp_2,self.c)
        for i,v in enumerate(tmp_2):
            ans_2 += v
        if flag == 2 and (len(ans_1) < len(ans_2) or (len(ans_1) == len(ans_2) and ans_1 < ans_2)):
            return ans_2
        return ans_1

矩阵中的最长递增路径

https://www.lintcode.com/problem/longest-increasing-path-in-a-matrix/solution?utm_source=sc-zhihu-sy0125-1

困难

给出一个矩阵，矩阵内的元素都是整数。
你需要找出矩阵中的一条最长的递增路径，并返回它的长度。
路径可以以矩阵中任何一个坐标作为起点，每次向上、下、左、右四个方向移动，并保证移动路线上的数字递增。
你不可以走出这个矩阵。

数据保证矩阵的行数和列数不超过200。

样例

样例 1：

输入： 
[[1,2,3],[6,5,4],[7,8,9]]
输出： 
9
解释： 
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9

样例 2：

输入： 
[[9,8,3],[9,2,1],[6,5,7]]
输出： 
5
解释： 
9 -> 6 -> 5 -> 2 -> 1

利用dfs来扫描所有可能的路径 用dp数组记录从(i, j)出发的最长递增路径，以此防止重复计算

时间复杂度：O(nm) 因为每个点都只访问了一遍

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y


class Solution(object):
    def longestIncreasingPath(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: int
        """
        if not matrix or not matrix[0]:
            return 0
        
        res = 0
        n, m = len(matrix), len(matrix[0])
        
        # dp[i][j]表示从(i, j)点出发获得的Longest Increasing Path
        dp = [[0 for j in xrange(m)] for i in xrange(n)] 
        
        for i in xrange(n):
            for j in xrange(m):
                res = max(res, self.dfs(matrix, Point(i, j), dp))
        return res
        
    def dfs(self, matrix, point, dp):  
        n, m = len(matrix), len(matrix[0])
        
        if dp[point.x][point.y] != 0:
            return dp[point.x][point.y]
        
        for dx, dy in [[-1, 0], [1, 0], [0, -1], [0, 1]]:
            x = point.x + dx
            y = point.y + dy

            if x < 0 or x >= n:
                continue

            if y < 0 or y >= m:
                continue
            
            if matrix[x][y] <= matrix[point.x][point.y]:
                continue
                
            # 从四周选一个最长的path
            dp[point.x][point.y] = max(dp[point.x][point.y], self.dfs(matrix, Point(x, y), dp))
            
        dp[point.x][point.y] += 1  # 再加上当前点
        
        return dp[point.x][point.y]

Python3 和 Longest Continuous Increasing subsequence II 一模一样..

DP

因为这种写法要sort, 时间复杂度 O(NlogN), N = m*n 空间复杂度O(N)

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

DIRECTIONS = [(1, 0), (-1, 0), (0, -1), (0, 1)]
class Solution:
    """
    @param matrix: an integer matrix
    @return: the length of the longest increasing path
    """
    def longestIncreasingPath(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: int
        """
        if not matrix or not matrix[0]:
            return 0
        sequence = []
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                sequence.append((matrix[i][j], i, j))
        sequence.sort()
        
        check = {}
        for h, x, y in sequence:
            cur_pos = (x, y)
            if cur_pos not in check:
                check[cur_pos] = 1
            cur_path = 0
            for dx, dy in DIRECTIONS:
                if self.is_valid(x+dx, y+dy, matrix, h):
                    cur_path = max(cur_path, check[(x+dx, y+dy)])
            check[cur_pos] += cur_path
        
        vals = check.values()
        return max(vals)
    
    def is_valid(self, x, y, matrix, h):
        row, col = len(matrix), len(matrix[0])
        return x >= 0 and x < row and y >= 0 and y < col and matrix[x][y] < h

DP版

这个题目可以DP， 但是需要按值重新排列一下。 然后再用LCS的方法做即可。 算法班讲过

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

DIR = [-1, 0, 1, 0, -1]

class Solution:
    """
    @param matrix: A matrix
    @return: An integer.
    """
    def longestIncreasingPath(self, matrix):
        points = []
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                points.append((matrix[i][j], i, j))
        points.sort()

        parsed_to_index = {}
        dp = [1] * len(points)
        max_length = 0
        for i in range(len(points)):
            for j in range(len(DIR) - 1):
                x = points[i][1] + DIR[j]
                y = points[i][2] + DIR[j + 1]
                if (x, y) in parsed_to_index:
                    k = parsed_to_index[(x, y)]
                    if points[i][0] > points[k][0]:
                        dp[i] = max(dp[i], dp[k] + 1)
                        max_length = max(max_length, dp[i])
            parsed_to_index[(points[i][1], points[i][2])] = i
        return max(dp)

解法：记忆化搜索+深度优先搜索

算法 / 数据结构：dfs(深度优先搜索）

解题思路

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

这道题普通的搜索是会超时的，于是我们选择优化的方法，记忆化搜索+深度优先搜索。
首先，我们从每个点开始遍历，深度优先搜索找到最长递增路径，在递归的过程中，我们要分四个方向进行讨论，若该点被搜索过，直接调用vis中保存的数组，并且返回结果。

复杂度分析

时间复杂度：O(nm) 和 O(V+E)

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

其中 n 和 m 是矩阵的行和列，nm为矩阵的大小。
深度优先搜索的时间复杂度是 O(V+E)，其中 V 是节点数，E 是边数。

空间复杂度：O(nm)

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

其中 n 和 m 是矩阵的行和列，nm为矩阵的大小。

源代码

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

def __init__(self):
        self.DIRECTIONS = [[0, 1], [1, 0], [0, -1], [-1, 0]]

    def longestIncreasingPath(self, matrix):
        indegrees = self.get_indegrees(matrix)
        queue = collections.deque()
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if indegrees[(i, j)] == 0:
                    queue.append((i, j))

        path_length = 0
        while queue:
            n = len(queue)
            
            path_length += 1
            for _ in range(n):
                x, y = queue.popleft()
                for direction in self.DIRECTIONS:
                    new_x = x + direction[0]
                    new_y = y + direction[1]
                    if not self.is_valid(new_x, new_y, matrix):
                        continue
                    if matrix[x][y] <= matrix[new_x][new_y]:
                        continue
                    indegrees[(new_x, new_y)] -= 1
                    if indegrees[(new_x, new_y)] == 0:
                        queue.append((new_x, new_y))
        
        return path_length

    def get_indegrees(self, matrix):
        indegrees = {}
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                indegrees[(i, j)] = 0
                for direction in self.DIRECTIONS:
                    new_x = i + direction[0]
                    new_y = j + direction[1]
                    if not self.is_valid(new_x, new_y, matrix):
                        continue
                    if matrix[i][j] < matrix[new_x][new_y]:
                        indegrees[(i, j)] += 1

        return indegrees

    def is_valid(self, x, y, matrix):
        if x < 0 or x >= len(matrix):
            return False
        if y < 0 or y >= len(matrix[0]):
            return False
        return True

算法：BFS、拓扑排序

思路：

使用求解拓扑排序的算法，使用分层BFS，层数就是最长路径长。 虽然是求递增序列长，但是建图时要使用大的数字向小的数字建立有向边，也就是说在求拓扑排序的时候是从一个数值相对大的点搜索到数值相对小的点。

复杂度分析

以下的 n 和 m 是矩阵的行数和列数。

时间复杂度：O(n * m)

空间复杂度：O(n * m)

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    def __init__(self):
        self.DIRECTIONS = [[0, 1], [1, 0], [0, -1], [-1, 0]]

    def longestIncreasingPath(self, matrix):
        indegrees = self.get_indegrees(matrix)
        queue = collections.deque()
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if indegrees[(i, j)] == 0:
                    queue.append((i, j))

        path_length = 0
        while queue:
            path_length += 1
            n = len(queue)
            for _ in range(n):
                x, y = queue.popleft()
                for direction in self.DIRECTIONS:
                    new_x = x + direction[0]
                    new_y = y + direction[1]
                    if not self.is_valid(new_x, new_y, matrix):
                        continue
                    if matrix[x][y] <= matrix[new_x][new_y]:
                        continue
                    indegrees[(new_x, new_y)] -= 1
                    if indegrees[(new_x, new_y)] == 0:
                        queue.append((new_x, new_y))
        
        return path_length

    def get_indegrees(self, matrix):
        indegrees = {}
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                indegrees[(i, j)] = 0
                for direction in self.DIRECTIONS:
                    new_x = i + direction[0]
                    new_y = j + direction[1]
                    if not self.is_valid(new_x, new_y, matrix):
                        continue
                    if matrix[i][j] < matrix[new_x][new_y]:
                        indegrees[(i, j)] += 1

        return indegrees

    def is_valid(self, x, y, matrix):
        if x < 0 or x >= len(matrix):
            return False
        if y < 0 or y >= len(matrix[0]):
            return False
        return True

Top Down Solution With Memoization 遍历每个点，搜索比起小的最长子串长度并使用boolean数组进行记忆化搜索

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param matrix: an integer matrix
    @return: the length of the longest increasing path
    """
    def longestIncreasingPath(self, matrix):
        if len(matrix) == 0 or len(matrix[0]) == 0:
            return 0
            
        n, m = len(matrix), len(matrix[0])
        
        count = 0
        dp = [[0 for i in range(m)]for j in range(n)]
        computed = [[False for i in range(m)]for j in range(n)]
        
        for i in range(n):
            for j in range(m):
                count = max(count, self.rec(matrix, dp, computed, i, j, n, m))
        
        return count
    
    def rec(self, matrix, dp, computed, i, j, n, m):
        if computed[i][j]:
            return dp[i][j]
        
        value = 1
        
        if self.inrange(i+1, j, n, m) and matrix[i][j] < matrix[i+1][j]:
            value = max(value, self.rec(matrix, dp, computed, i+1, j, n, m) + 1)
        if self.inrange(i-1, j, n, m) and matrix[i][j] < matrix[i-1][j]:
            value = max(value, self.rec(matrix, dp, computed, i-1, j, n, m) + 1)
        if self.inrange(i, j+1, n, m) and matrix[i][j] < matrix[i][j+1]:
            value = max(value, self.rec(matrix, dp, computed, i, j+1, n, m) + 1)
        if self.inrange(i, j-1, n, m) and matrix[i][j] < matrix[i][j-1]:
            value = max(value, self.rec(matrix, dp, computed, i, j-1, n, m) + 1)
            
        dp[i][j] = value
        computed[i][j] = True
        
        return dp[i][j]
        
    def inrange(self, i, j, n, m):
        return 0 <= i < n and 0 <= j < m

Top Down Solution With Memoization 遍历每个点，搜索比起小的最长子串长度并使用boolean数组进行记忆化搜索

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param matrix: an integer matrix
    @return: the length of the longest increasing path
    """
    def longestIncreasingPath(self, matrix):
        if len(matrix) == 0 or len(matrix[0]) == 0:
            return 0
            
        n, m = len(matrix), len(matrix[0])
        
        count = 0
        dp = [[0 for i in range(m)]for j in range(n)]
        computed = [[False for i in range(m)]for j in range(n)]
        
        for i in range(n):
            for j in range(m):
                count = max(count, self.rec(matrix, dp, computed, i, j, n, m))
        
        return count
    
    def rec(self, matrix, dp, computed, i, j, n, m):
        if computed[i][j]:
            return dp[i][j]
        
        value = 1
        
        if self.inrange(i+1, j, n, m) and matrix[i][j] < matrix[i+1][j]:
            value = max(value, self.rec(matrix, dp, computed, i+1, j, n, m) + 1)
        if self.inrange(i-1, j, n, m) and matrix[i][j] < matrix[i-1][j]:
            value = max(value, self.rec(matrix, dp, computed, i-1, j, n, m) + 1)
        if self.inrange(i, j+1, n, m) and matrix[i][j] < matrix[i][j+1]:
            value = max(value, self.rec(matrix, dp, computed, i, j+1, n, m) + 1)
        if self.inrange(i, j-1, n, m) and matrix[i][j] < matrix[i][j-1]:
            value = max(value, self.rec(matrix, dp, computed, i, j-1, n, m) + 1)
            
        dp[i][j] = value
        computed[i][j] = True
        
        return dp[i][j]
        
    def inrange(self, i, j, n, m):
        return 0 <= i < n and 0 <= j < m

Top Down Solution With Memoization 遍历每个点，搜索比起小的最长子串长度并使用boolean数组进行记忆化搜索

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param matrix: an integer matrix
    @return: the length of the longest increasing path
    """
    def longestIncreasingPath(self, matrix):
        if len(matrix) == 0 or len(matrix[0]) == 0:
            return 0
            
        n, m = len(matrix), len(matrix[0])
        
        count = 0
        dp = [[0 for i in range(m)]for j in range(n)]
        computed = [[False for i in range(m)]for j in range(n)]
        
        for i in range(n):
            for j in range(m):
                count = max(count, self.rec(matrix, dp, computed, i, j, n, m))
        
        return count
    
    def rec(self, matrix, dp, computed, i, j, n, m):
        if computed[i][j]:
            return dp[i][j]
        
        value = 1
        
        if self.inrange(i+1, j, n, m) and matrix[i][j] < matrix[i+1][j]:
            value = max(value, self.rec(matrix, dp, computed, i+1, j, n, m) + 1)
        if self.inrange(i-1, j, n, m) and matrix[i][j] < matrix[i-1][j]:
            value = max(value, self.rec(matrix, dp, computed, i-1, j, n, m) + 1)
        if self.inrange(i, j+1, n, m) and matrix[i][j] < matrix[i][j+1]:
            value = max(value, self.rec(matrix, dp, computed, i, j+1, n, m) + 1)
        if self.inrange(i, j-1, n, m) and matrix[i][j] < matrix[i][j-1]:
            value = max(value, self.rec(matrix, dp, computed, i, j-1, n, m) + 1)
            
        dp[i][j] = value
        computed[i][j] = True
        
        return dp[i][j]
        
    def inrange(self, i, j, n, m):
        return 0 <= i < n and 0 <= j < m

两数之和

简单

给一个整数数组，找到两个数使得他们的和等于一个给定的数 target。

你需要实现的函数twoSum需要返回这两个数的下标, 并且第一个下标小于第二个下标。注意这里下标的范围是 0 到 n-1。

你可以假设只有一组答案。

样例

样例1:
给出 numbers = [2, 7, 11, 15], target = 9, 返回 [0, 1].
样例2:
给出 numbers = [15, 2, 7, 11], target = 9, 返回 [1, 2].

挑战

给自己加点挑战

• $O(n)$ 空间复杂度，$O(nlogn)$ 时间复杂度，

• $O(n)$ 空间复杂度，$O(n)$ 时间复杂度，

Given an array of integers, find two numbers such that they add up to a specific target number.

The function twoSum should return indices of the two numbers such that they add up to the target, where index1 must be less than index2. Please note that your returned answers (both index1 and index2) are not zero-based.

You may assume that each input would have exactly one solution.

Input: numbers={2, 7, 11, 15}, target=9 Output: index1=1, index2=2

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution(object):
    def twoSum(self, nums, target):
        #hash用于建立数值到下标的映射
        hash = {}
        #循环nums数值，并添加映射
        for i in range(len(nums)):
            if target - nums[i] in hash:
                return [hash[target - nums[i]], i]
            hash[nums[i]] = i
        #无解的情况
        return [-1, -1]

使用双指针算法，时间复杂度 $(nlogn)$，空间复杂度 $O(n)$

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1, index2] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        if not numbers:
            return [-1, -1]
        
        # transform numbers to a sorted array with index
        nums = [
            (number, index)
            for index, number in enumerate(numbers)
        ]
        nums = sorted(nums)
        
        left, right = 0, len(nums) - 1
        while left < right:
            if nums[left][0] + nums[right][0] > target:
                right -= 1
            elif nums[left][0] + nums[right][0] < target:
                left += 1
            else:
                return sorted([nums[left][1], nums[right][1]])
        
        return [-1, -1]

要返回的是原数组的index而不是排序之后的数组

所以 argsort 一下原数组, 获取到排序后原数组的 index

然后正常排序 Two Pointers 做

目测我这个版本最简单?

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1, index2] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        # write your code here
        if not numbers or len(numbers) < 2:
            return [-1, -1]

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

    arg_nums = [x for x, y in sorted(enumerate(numbers), key = lambda x: x[1])]
    numbers.sort()
    left, right = 0, len(numbers) - 1
    while left <= right:
        if numbers[left] + numbers[right] == target:
            return sorted([arg_nums[left], arg_nums[right]])
        elif numbers[left] + numbers[right] < target:
            left += 1
        else:
            right -= 1

    return [-1, -1]

python双指针解法：sort array后运用相向双指针法。 找到目标pair的value后，重新找回它们在原array中的index。

注意最后找回index value时，如果pair里的两数相同需要特殊处理。

每一步复杂度分析： copy array: O(n), sort array: O(nlogn), 双指针找target pair: O(n), 找回原先的index：O(nlog)+O(nlogn) 总复杂度:O(nlogn)

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1, index2] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        # write your code here
        if not numbers:
            return -1
        nums = sorted(numbers)
        #print(nums)
        left, right = 0, len(numbers) - 1 
        while left < right:
            #print('left, right', left, right)
            if nums[left] + nums[right] == target:


                #print('yes')  #所以这种方法不行
                #array.index(x)   Return the smallest i such that i is the index of the first occurrence of x in the array.
                i = numbers.index(nums[left])
                j = numbers.index(nums[right])
                print('i, j',i, j)
                if i == j:  ##两个重复的数字时候，index只能返回最小的指针
                    k = numbers[i+1:].index(nums[right]) + i + 1
                    return [i, k]
                elif i < j:
                    return [i, j] 
                else:
                    return [j, i]
                #return [numbers.index(nums[left]), numbers.index(nums[right])]
            if nums[left] + nums[right] < target:
                left += 1 
            if nums[left] + nums[right] > target:
                right -= 1 
        return -1
                
numbers = [0,4,3,0]
target = 0
obj = Solution()
result = obj.twoSum(numbers, 0)
print(result)

一种python解法

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1 + 1, index2 + 1] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        for i, a in enumerate(numbers):
            for j, b in enumerate(numbers[i + 1 - len(numbers):]):
                if a + b == target:
                    return [i, j + i + 1]
        return [-1, -1]

双指针的解法，时间复杂度O(NlogN)。 要求返回的是原来位置的下标，这个问题使用双指针的解法需要排序，所以要构建一个pair来记录原始的下标。

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1, index2] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        # write your code here
        self.construct_pairs(numbers)
        sorted_nums_pair = sorted(numbers, key = lambda x : x[1])
        
        left_idx = 0
        right_idx = len(numbers) - 1 
        
        while left_idx < right_idx:
            if sorted_nums_pair[left_idx][1] + sorted_nums_pair[right_idx][1] == target:
                return [min(sorted_nums_pair[left_idx][0], sorted_nums_pair[right_idx][0]),
                        max(sorted_nums_pair[left_idx][0], sorted_nums_pair[right_idx][0])]
            
            if sorted_nums_pair[left_idx][1] + sorted_nums_pair[right_idx][1] < target:
                left_idx += 1 
            else:
                right_idx -= 1 
        
        return []
    
    def construct_pairs(self, nums):
        for i, num in enumerate(nums):
            nums[i] = [i, num]

算法：hashmap

用map记录所有当前查找过的num[i]，存下target-num[i]

如果存在num[j]在map中说明存在一对i,j的使得num[i],num[j]和为target，

即找到了答案

复杂度分析

• 时间复杂度O(n)

• n为数组的大小

• 空间复杂度O(n)

• n为数组的大小

算法：双指针

先对数组拷贝

然后对数组排序，在排序后的数组中利用双指针从左右向中间寻找

• 如果numbers[i] + numbers [j] == target 说明找到答案

• 如果numbers[i] + numbers [j] < target 说明当前和比答案小。左指针右移

• 如果numbers[i] + numbers [j] > target 说明当前和比答案大。右指针左移

然后在拷贝数组中找到对应numbers[i]和numbers[j] 的下标，对这两个下标排个序

复杂度分析

• 时间复杂度O(nlogn)

• n为数组的大小

• 空间复杂度O(n)

• n为数组的大小

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

//hashmap
class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1, index2] (index1 < index2)
    """
    def twoSum(self, nums, target):
        um = dict()
        for i in range(len(nums)):
        #查找是否存在满足一个数+nums[i]==target
            if nums[i] in um:
                result=[]
                result.append(um[nums[i]])
                result.append(i)
                return result
            um[target-nums[i]] = i;
        return [0,0]
//双指针
class Solution:
    """
    @param numbers : An array of Integer
    @param target : target = numbers[index1] + numbers[index2]
    @return : [index1 + 1, index2 + 1] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        backUp = numbers[:]
        numbers = sorted(numbers)
        i,j = 0,len(numbers) - 1
        while i < j:
            # 找到答案
            if numbers[i] + numbers [j] == target:
                break
            # 左指针右移
            elif numbers[i] + numbers [j] < target:
                i += 1
            # 右指针左移
            else:
                j -= 1
        a,b = 0,0 #标记是否找到，避免i，j值相同的情况
        for k in range(len(backUp)):
            #查找对应下标
            if backUp[k] == numbers[i] and a == 0:
                i = k
                a = 1
            elif backUp[k] == numbers[j] and b == 0:
                j = k
                b = 1
            elif a == 1 and b == 1:
                break
        return sorted([i,j])

create a dictionary to record all the number and index. Then traverse the list and check if target-number exist in dictionary.

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1, index2] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        # write your code here
        dic = {}
        res = []
        for i in range(len(numbers)):
            dic[numbers[i]] = i
        
        
        for i in range(len(numbers)):
            if i not in res:
                tmp = target-numbers[i]
                if tmp in dic and i<dic[tmp]:
                    res.append(i)
                    res.append(dic[tmp])
                
        return res

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param numbers: An array of Integer
    @param target: target = numbers[index1] + numbers[index2]
    @return: [index1, index2] (index1 < index2)
    """
    def twoSum(self, numbers, target):
        # write your code here
        if not numbers:
            return [-1, -1]
        
        # time complexity O(n)
        dict_num_index = {}
        for i, val in enumerate(numbers):
            dict_num_index[val] = i 
        
        for i, val in enumerate(numbers):
            target2 = target - val 
            if target2 in dict_num_index:
                return [i, dict_num_index[target2]]
        
        return [-1, -1]

反转字符串 III

简单

给定一个字符串句子，反转句子中每一个单词的所有字母，同时保持空格和最初的单词顺序。

字符串中，每一个单词都是由空格隔开，字符串中不会有多余的空格。

样例

输入: "Let's take LeetCode contest"
输出: "s'teL ekat edoCteeL tsetnoc"

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param s: a string
    @return: reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order
    """

    def reverseWords(self, s):
        # Write your code here
        word = ""
        answer = ""
        for c in s:
            if c == ' ':
                if word != "":
                    answer += word[::-1]
                word = ""
                answer += c
            else:
                word += c
        if word != "":
            answer += word[::-1]
        return answer

利用 Python 字符串的 split() 、反转方法（s[::-1]）和 join() 轻松通关`

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    def reverseWords(self, s): return " ".join([i[::-1] for i in s.split()])
    
    
   
   
 乘积最大子序列   
   
找出一个序列中乘积最大的连续子序列（至少包含一个数）。
It is guaranteed that the length of nums doesn't exceed 20000
The product of the subsequence with maximum product, less than 2147483647
样例
样例 1:
输入:[2,3,-2,4]
输出:6

样例 2:
输入:[-1,2,4,1]
输出:8

这道题和maximal subarray思路一样，不同的是对于加法加上负数会变小，加上正数会变大；而对于乘法，乘以正数有可能变大也有可能变小（原数是负数的情况下），乘以负数也有可能变大或者变小
所以需要两个变量： min_p表示行进到当前subarray能得到的最小的积 max_p表示行进到当前subarray能得到的最大的积
对于某一个subarray来说，它最大的积，有可能来自之前的最大积乘以一个正数，或者之前的最小积乘以一个负数，或者numsi就是最大的 因此 max_p = max(numsi, max_p numsi, min_p numsi) 最小积同理
最后用res变量跟踪一下全局最大
/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution(object):
    def maxProduct(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not nums:
            return 0
        
        res = nums[0]
        min_p = max_p = nums[0]
        for i in xrange(1, len(nums)):
            tmp = min_p
            min_p = min(nums[i], min_p * nums[i], max_p * nums[i])
            max_p = max(nums[i], max_p * nums[i], tmp * nums[i])
            res = max(res, max_p)
        return res

动态规划，先用数组的方式写一遍，熟悉思路；然后优化空间复杂度，用变量代替数组。

【确认条件】 （1）本题中是可以有负数的，如果只有正数，会更简单。 （2）思考一下numsi为0时会不会有corner case。 （3）确认异常输入的检测与返回值。

【解题思路】 （1）确定状态： 先假设所有值为正数，如果以当前序列以numsi结尾, 那么乘积最大的就是以numsi - 1为结尾的序列的最大乘积, 再乘numsi。 此时答案为：遍历以numsi为结尾的所有n个序列，找到连乘积最大的那个。

如果numsi为负数，那么此时乘积最大值就是以numsi - 1为结尾的序列的最小乘积, 再乘上numsi。 因此我们需要两个状态数组记录状态：max_arri用于记录最大值, min_arri用于记录最小值。

为了求max_arri 和 min_arri，我们需要先获得max_arri - 1和 min_arri - 1。 最终答案为max(max_arr)。

（2）转移方程： 如果numsi > 0 max_arri = max(max_arri, max_arri - 1 numsi) min_arri = min(min_arri, min_arri - 1 numsi)

如果numsi < 0 max_arri = max(max_arri, min_arri - 1 numsi) min_arri = min(min_arri, max_arri - 1 numsi)

（3）初始状态和边界情况： 因为序列长度最小为1，所以候选序列至少得考虑当前numsi的值。 所以max_arr和min_arr初始化的时候，直接深度复制nums。

（4）计算顺序： 从nums1到numsn - 1。

【优化思路】 观察发现max_arri 和 min_arri至于前一状态max_arri - 1和 min_arri - 1有关，所以没有必要使用数组来保存状态，可以简化为状态变量，空间上可以减少一个维度。

所以用prev_max, prev_min来记录以numsi - 1为结尾序列的最大/最小乘积，以cur_max, cur_min来记录以numsi为结尾序列的最大/最小乘积。

另外可以偷懒把numsi是否大于0的判断融合进max，min操作中（虽然增加了运算，但是复杂度的维度不变）。

【实现要点】 在使用数组的时候，初始化max_arr和min_arr要分别深度copy。

【复杂度】 时间复杂度：O(n) 空间复杂度：O(1)

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

# 把数组简化为变量的DP写法
class Solution:
    def maxProduct(self, nums):
        if not nums:
            return None
            
        global_max = cur_max = cur_min = nums[0]
        
        for num in nums[1:]:
            prev_max, prev_min = cur_max, cur_min
            cur_max = max(num, prev_max * num, prev_min * num)
            cur_min = min(num, prev_max * num, prev_min * num)
            global_max = max(global_max, cur_max)
            
        return global_max


# 使用数组的DP写法
class Solution:
    def maxProduct(self, nums):
        if not nums:
            return None
        
        min_arr = nums[::]
        max_arr = nums[::]
        
        for i in range(1, len(nums)):
            if nums[i] > 0:
                max_arr[i] = max(max_arr[i], max_arr[i - 1] * nums[i])
                min_arr[i] = min(min_arr[i], min_arr[i - 1] * nums[i])
            elif nums[i] < 0:
                max_arr[i] = max(max_arr[i], min_arr[i - 1] * nums[i])
                min_arr[i] = min(min_arr[i], max_arr[i - 1] * nums[i])
        
        return max(max_arr)

动态规划加滚动数组, 相对好理解一点。 转移方程 Maxi=max{ai, Maxi-1ai, Mini-1ai}; Mini=min{ai, Maxi-1ai, Mini-1ai}; maxProduct = max(maxProduct, Maxi)

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param nums: An array of integers
    @return: An integer
    """
    def maxProduct(self, nums):
        # write your code here
        if not nums:
            return 0
        if len(nums) == 1:
            return nums[0]
            
        dp_max = [0] * 2
        dp_min = [0] * 2
        max_product = nums[0]
        dp_max[0] = nums[0]
        dp_min[0] = nums[0]
        for i in range(1, len(nums)):
            dp_max[i%2] = max(nums[i], dp_max[(i-1) % 2] * nums[i], dp_min[(i-1) % 2] * nums[i])
            dp_min[i%2] = min(nums[i], dp_max[(i-1) % 2] * nums[i], dp_min[(i-1) % 2] * nums[i])
            max_product = max(max_product, dp_max[i%2])
            
        return max_product

mx 传递最大值，mn 传递最小值

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    
    def maxProduct(self, nums):
        
        result = nums[0]
        mx, mn = 1, 1 
        for num in nums:
            choices = num, mx * num, mn * num 
            mx, mn = max(choices), min(choices)
            result = max(result, mx)
        return result

算法：dp

比较容易想出来的线性dp。由于数据中有正有负，所以我们利用两个dp数组来完成。用fi来保存计算到第i个时的最大值，用gi来保持计算到第i个时的最小值。

• 在得出了第i-1的dp值之后，即包含i-1的可能值区间为[gi-1,fi-1]（左闭右闭区间）。我们考虑第i个数的情况。

• 若numsi为正数，可能值区间为[gi-1×numsi,fi-1×numsi]，和numsi。

• 若numsi为负数，可能值区间为[fi-1×numsi,gi-1×numsi]，和numsi。

• 所以我们直接根据上述的情况，就能得出包含numsi的最大值fi=max(max(fi-1×numsi, gi-1×numsi), numsi)。同理，gi=min(min(fi-1*×i, gi-1×numsi), numsi)。

• 最后由于我们要求的是最大值，直接对f数组取最大值即可。

复杂度分析

• 时间复杂度O(n)

• 枚举了数组的长度

• 空间复杂度O(n)

• 消耗了等长的空间

**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param nums: An array of integers
    @return: An integer
    """
    def maxProduct(self, nums):
        if not nums:
            return None
            
        global_max = prev_max = prev_min = nums[0]
        for num in nums[1:]:
            if num > 0:
                curt_max = max(num, prev_max * num)
                curt_min = min(num, prev_min * num)
            else:
                curt_max = max(num, prev_min * num)
                curt_min = min(num, prev_max * num)
            
            global_max = max(global_max, curt_max)
            prev_max, prev_min = curt_max, curt_min
            
        return global_max

算法：dp

比较容易想出来的线性dp。由于数据中有正有负，所以我们利用两个dp数组来完成。用fi来保存计算到第i个时的最大值，用g[i]来保持计算到第i个时的最小值。

• 在得出了第i-1的dp值之后，即包含i-1的可能值区间为[g[i-1],f[i-1]]（左闭右闭区间）。我们考虑第i个数的情况。

• 若nums[i]为正数，可能值区间为[g[i-1]×nums[i],f[i-1]×nums[i]]，和nums[i]。

• 若nums[i]为负数，可能值区间为[f[i-1]×nums[i],g[i-1]×nums[i]]，和nums[i]。

• 所以我们直接根据上述的情况，就能得出包含nums[i]的最大值f[i]=max(max(f[i-1]×nums[i], g[i-1]×nums[i]), nums[i])。同理，g[i]=min(min(f[i-1]*×[i], g[i-1]×nums[i]), nums[i])。

• 最后由于我们要求的是最大值，直接对f数组取最大值即可。

复杂度分析

• 时间复杂度O(n)

• 枚举了数组的长度 

• 空间复杂度O(n)

• 消耗了等长的空间

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */


# 本参考程序来自九章算法，由 @ 提供。版权所有，转发请注明出处。

# - 九章算法致力于帮助更多中国人找到好的工作，教师团队均来自硅谷和国内的一线大公司在职工程师。

# - 现有的面试培训课程包括：九章算法班，系统设计班，算法强化班，Java入门与基础算法班，Android 项目实战班，

# - Big Data 项目实战班，算法面试高频题班, 动态规划专题班

# - 更多详情请见官方网站：[http://www.jiuzhang.com/?source=code](http://www.jiuzhang.com/?source=code)


class Solution:

    """

    @param nums: An array of integers

    @return: An integer

    """

    def maxProduct(self, nums):

        if not nums:

            return None

            

        global_max = prev_max = prev_min = nums[0]

        for num in nums[1:]:

            if num > 0:

                curt_max = max(num, prev_max * num)

                curt_min = min(num, prev_min * num)

            else:

                curt_max = max(num, prev_min * num)

                curt_min = min(num, prev_max * num)

            

            global_max = max(global_max, curt_max)

            prev_max, prev_min = curt_max, curt_min

            

        return global_max

提供一种双记忆数组加最后比较的算法 在最后进行max查找 防止在loop中比较时候犯头晕

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

def maxProduct(self, nums):
        # write your code here
        if not nums:
            return 0
        if len(nums) == 1:
            return nums[0]
        
        MAX = 100000000
        MIN = - MAX
        max_value = [MIN for _ in range(len(nums))]
        min_value = [MAX for _ in range(len(nums))]
        max_value[0], min_value[0] = nums[0], nums[0]
        
        for i in range(1, len(nums)):
            max_value[i] = max(nums[i], max_value[i - 1] * nums[i], min_value[i - 1] * nums[i])
            min_value[i] = min(nums[i], max_value[i - 1] * nums[i], min_value[i - 1] * nums[i])
        
        # 记住 此题的确定状态不是最后一个对应的值 而是所有数组中的最大值
        return max(max_value)

最大值和最小值都要记录，因为有负数存在。一开始很大也可能乘了负数变成最小值，最小值也可能变成最大的。因此都要记录。

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        
        low_now = high = high_now = nums[0]
        for i in range(1, len(nums)):
            temp = high_now
            high_now = max(low_now*nums[i], high_now*nums[i], nums[i])
            low_now = min(low_now*nums[i], temp*nums[i], nums[i])
            high = max(high, high_now)
        return high

 最长回文子串

中等

给出一个字符串（假设长度最长为1000），求出它的最长回文子串，你可以假定只有一个满足条件的最长回文串。

样例

样例 1:

输入:"abcdzdcab"
输出:"cdzdc"

样例 2:

输入:"aba"
输出:"aba"

挑战

时间复杂度可为O(n2)，你能将其优化为O(n)吗

这里很热闹，同学们很踊跃，可能是令狐冲老师的免费公开课的原因？

这么多解法，你该看那个？你要是自己写不出来，你该背那个？

马拉车肯定不行，动态规划是可以的，可是面试时你可能一紧张，太复杂，想不起来。

所以这个背向双指针的代码最适合你。这个双指针写法不一定是双指针里最好的，但可能是最容易背的。

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    
    def longestPalindrome(self, s):
        
        self.longest_string = ''
        
        for mid in range(len(s)):
            
            self.extends_palindrome(s, mid, mid)
            
            self.extends_palindrome(s, mid, mid+1)
                
        return self.longest_string
        
    def extends_palindrome(self, s, lo, hi):
        
        while lo >= 0 and hi < len(s) and s[lo] == s[hi]:
            lo -= 1 
            hi += 1 
            
        lo += 1 
        
        if hi - lo > len(self.longest_string):
            self.longest_string = s[lo:hi]

基于区间型动态规划的解法

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        if not s:
            return ""
            
        n = len(s)
        is_palindrome = [[False] * n for _ in range(n)]
        
        for i in range(n):
            is_palindrome[i][i] = True
        for i in range(1, n):
            is_palindrome[i][i - 1] = True
            
        longest, start, end = 1, 0, 0
        for length in range(1, n):
            for i in range(n - length):
                j = i + length
                is_palindrome[i][j] = s[i] == s[j] and is_palindrome[i + 1][j - 1]
                if is_palindrome[i][j] and length + 1 > longest:
                    longest = length + 1
                    start, end = i, j
                    
        return s[start:end + 1]

基于中心线枚举的方法

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        # 重点1：任何代码都要进行异常检测
        if not s:
            return ""
        
        # 重点2：用空行区分开异常检测部分，核心代码部分，和返回值部分，属于高端代码风格技巧
        longest = ""
        for middle in range(len(s)):
            # 重点3：子函数化避免重复代码
            sub = self.find_palindrome_from(s, middle, middle)
	        # 重点4：通过返回值来避免使用全局变量这种不好的代码风格
            if len(sub) > len(longest):
                longest = sub
            sub = self.find_palindrome_from(s, middle, middle + 1)
            if len(sub) > len(longest):
                longest = sub
                
		# 重点2：用空行区分开异常检测部分，核心代码部分，和返回值部分，属于高端代码风格技巧
        return longest
        
    def find_palindrome_from(self, string, left, right):
        while left >= 0 and right < len(string):
            # 重点5：将复杂判断拆分到 while 循环内部，而不是放在 while 循环中，提高代码可读性
            if string[left] != string[right]:
                break
            left -= 1
            right += 1
            
        return string[left + 1:right]

动态规划版本： 1. 先创建一个二维数组DP， 全部置为False， 同时设置最大回文串长度为0以及其初始位置 2. 循环第一遍， 把对角线置为True, 因为每单个字符都构成长度为1的回文串 3. 循环第二遍， 把连续两个字母相同出现的情况置为True 4. 两重循环， 根据动规转移方程写完剩下的DP矩阵，一边写一边更新最大回文串长度和初始位置 5. 打擂台， 取出最大的回文串长度和其初始位置， 返回结果

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        # write your code here

        n = len(s)
        maxLen = 0
        maxStartIndex = 0
        dp = [([False] * n) for i in range (n)]
        for i in range(n):
            dp[i][i] = True
            maxLen = 1
            maxStartIndex = i
        for i in range(n-1):
            if s[i] == s[i+1]:
                dp[i][i+1] = True
                maxLen = 2
                maxStartIndex = i
        for curLen in range(3, n+1):
            for startIndex in range(n-curLen+1):
                endIndex = startIndex + curLen - 1
                dp[startIndex][endIndex] = (dp[startIndex+1][endIndex-1] and s[startIndex] == s[endIndex])
                if dp[startIndex][endIndex] == True and curLen > maxLen:
                    maxLen = curLen
                    maxStartIndex = startIndex
        return s[maxStartIndex:maxStartIndex + maxLen]

方法一

解题思路

最暴力的想法是，枚举子串的头尾，判断该子串是否是回文串。

复杂度分析

设字符串的长度为 N。

时间复杂度

• 枚举首尾的复杂度为 O(N^2)。

• check 一个字符串是否是回文，复杂度为 O(N)。

• 总时间复杂度为 O(N^3)。

空间复杂度

• 如果用substring函数取出子串并判断的话，空间复杂度为O(n)。

• 如果直接在原数组上对子串进行check的话，空间复杂度为o(1)。

方法二

解题思路

由回文串正序和反序的性质相同，可以得出一个性质，如果一个字符串，其中心不是回文串，那么它一定不是个回文串。所以我们每次从中心开始，向两边延展首尾，判断是否是回文串。

代码思路

1. 枚举中心 center，需要两个指针 start， end。

2. 如果 s[start] == s[end]，则 start--，end++，更新答案

3. 重复上一步，直到不相等就停止。

4. 注意：奇数和偶数长度的回文串是不同的，奇数中心是单独的一个字符，偶数的是相邻的两个字符。

复杂度分析

设字符串的长度为 N。

时间复杂度

• 枚举回文中心，复杂度 O(n)。

• 向两边延展并 check，复杂度 O(n)。

• 总时，时间复杂度为 O(n^2)。

空间复杂度

• 不需要额外变量，空间复杂度为 O(1)。

方法三

解题思路

由回文串正序和反序的性质相同，可以得出一个性质，如果一个字符串，其中心不是回文串，那么它一定不是个回文串。如果去掉头和尾，它依然还是一个回文串。在头和尾加上同一个字符也是一个回文串。

由此可以得出判断一个区间是否是回文串，可以由更小的区间得到，并且不受包含这个区间的大区间影响，所以满足无后效性且是最有子结构，可以用动态规划求解。

代码思路

动态规划

设dp(l, r)，代表区间[l, r]是否是回文串。

如果s[l] == s[r]，并且s[l + 1 ~ r - 1]是回文串的话，s[l ~ r]就是回文串。

复杂度分析

设字符串长度为 N。

时间复杂度

• 枚举端点，O(1)时间转移，时间复杂度为O(n^2)。

空间复杂度

• 需要额外O(n^2)空间记录dp值。

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

# 方法一
class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        length = len(s)
        max_len, result = 0, ""
        
        for start in range(length):
            for end in range(start, length):
                new_len = end - start + 1
                # 小优化
                if new_len <= max_len:
                    continue
                if self.is_palindrome(s[start : end + 1]):
                    max_len = new_len
                    result = s[start : end + 1]
        
        return result
    
    
    # 判断是否回文
    def is_palindrome(self, s):
        length = len(s)
        for i in range(length // 2):
            if s[i] != s[length - i - 1]:
                return False
        return True

# 方法二
class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        length = len(s)
        max_len, result = 0, ""
        
        for center in range(length):
            # 奇数情况
            start, end = center, center
            while self.valid(start, end, length):
                if s[start] != s[end]:
                    break
                new_len = end - start + 1
                if new_len > max_len:
                    max_len = new_len
                    result = s[start : end + 1]
                start -= 1
                end += 1
            
            # 偶数情况
            start, end = center, center + 1
            while self.valid(start, end, length):
                if s[start] != s[end]:
                    break
                new_len = end - start + 1
                if new_len > max_len:
                    max_len = new_len
                    result = s[start : end + 1]
                start -= 1
                end += 1
        return result
    
    # 判断指针范围是否合法
    def valid(self, start, end, length):
        return start > -1 and end < length

# 方法三
class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        length = len(s)
        max_len = 1
        start = 0
        is_palindrome = [[False] * length for _ in range(length)]
        
        # 将长度为 1 的 dp 值设为真
        for i in range(length):
            is_palindrome[i][i] = True;
        
        for i in range(length - 1):
            if s[i] == s[i + 1]:
                is_palindrome[i][i + 1] = True
                max_len = 2
                start = i
        
        for new_len in range(3, length + 1):
            for left in range(length - new_len + 1):
                right = left + new_len - 1
                if is_palindrome[left + 1][right - 1] and s[left] == s[right]:
                    is_palindrome[left][right] = True
                    # 更新答案
                    if new_len > max_len:
                        max_len = new_len
                        start = left
        
        return s[start : start + max_len]
``` for left in range(length - new_len + 1):
                right = left + new_len - 1
                if is_palindrome[left + 1][right - 1] and s[left] == s[right]:
                    is_palindrome[left][right] = True
                    # 更新答案
                    if new_len > max_len:
                        max_len = new_len
                        start = left
        
        return s[start : start + max_len]

相比于现在题解中的Python代码，优化了几个方面： 1.while循环代替for循环，因为for循环后期由于不可能超过最大值已经没有意义； 2.if i&1之后left和right直接赋值下一个要check的两个位置，省掉一拨循环 3.现题解中max的初值为0（应为1），后期赋值为right-left（应再调整1），进行了改正 4.现题解中left的初值为0，但right的初值为1，此处也不准确，right初值应为0，否则如果s='a'，输出将是s0:2，虽然能输出正确结果，但表达不精确 5.用//替代/改正了整除写法

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    def longestPalindrome(self, s):
        if s == None or len(s) == 0:
            return ""
        longest = 1
        start = 0
        end = 0
        i = 1
        while 2 * len(s) - 1 - i > longest:
            if i & 1:
                left = (i - 1) // 2
                right = left + 1
            else:
                left = i // 2 - 1
                right = left + 2
            while left >= 0 and right < len(s) and s[left] == s[right]:
            	left -= 1
                right += 1
            # left和right此时为试探失败的一对位置 
            if right - left - 1 > longest:
                longest = right - left - 1
                start = left + 1
                end = right - 1
            i += 1
        return s[start: end + 1]

使用同样结构的Brutal force (O(n^2)) 和 Manacher(O(n)) 两种算法

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        # write your code here
        def brutal_force(s,lengthPalindrome):
            size = len(new_s)
            length = 0
            longestPos = 0
            for i in range(size):
                l = 0
                while (i-l) >= 0 and (i+l) < size and new_s[i-l]==new_s[i+l]:
                    l += 1
                lengthPalindrome[i] = l
                if (l-1) > length:
                    length = l-1
                    longestPos = i
            return longestPos
            
        def manacher(s,lengthPalindrome):
            size = len(new_s)
            length = 0
            longestPos = 0
            right = 0
            pivot = 0
            for i in range(size):
                l = 0
                if i < right:
                    l = min(lengthPalindrome[2*pivot - i],right-i)
                while (i-l) >= 0 and (i+l) < size and new_s[i-l]==new_s[i+l]:
                    l += 1
                lengthPalindrome[i] = l
                if (l-1) > length:
                    length = l-1
                    longestPos = i
                # update pivot and right boundary 
                if i+l > right:
                    right = i+l
                    pivot = i
            return longestPos
                
                
        ans = ''
        new_s = '#'+'#'.join(s)+'#' # splited by '#'
        lengthPalindrome = [ 0 for _ in range(len(new_s)) ]
        #longestPos = brutal_force(new_s,lengthPalindrome)
        longestPos = manacher(new_s,lengthPalindrome)
        l = lengthPalindrome[longestPos]
        ans = s[(longestPos-l+1)/2:(longestPos+l-1)/2]
        return ans

使用 Manacher's Algorithm 可以在 O(n) 的时间内解决问题 参考资料：https://www.felix021.com/blog/read.php?2040

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    """
    @param s: input string
    @return: the longest palindromic substring
    """
    def longestPalindrome(self, s):
        if not s:
            return

        # Using manacher's algorithm
        # abba => #a#b#b#a#
        chars = []
        for c in s:
            chars.append('#')
            chars.append(c)
        chars.append('#')
        
        n = len(chars)
        palindrome = [0] * n
        palindrome[0] = 1
        
        mid, longest = 0, 1
        for i in range(1, n):
            length = 1
            if mid + longest > i:
                mirror = mid - (i - mid)
                length = min(palindrome[mirror], mid + longest - i)

            while i + length < len(chars) and i - length >= 0:
                if chars[i + length] != chars[i - length]:
                    break;
                length += 1
            
            if length > longest:
                longest = length
                mid = i
            
            palindrome[i] = length
        
        # remove the extra #
        longest = longest - 1
        start = (mid - 1) // 2 - (longest - 1) // 2
        return s[start:start + longest]

动态规划最好理解的方案，带注释

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

def longestPalindrome(self, s: str):
        n = len(s)
        dp = [[False] * n for _ in range(n)]
        ans = ""
        # 枚举子串的长度 l+1
        for l in range(n):
            # 枚举子串的起始位置 i，这样可以通过 j=i+l 得到子串的结束位置
            for i in range(n):
                j = i + l
                if j >= len(s):
                    break
            #判断几种情况0直接True，1考虑是否相等 ， 大于1需要dp转换
                if l == 0:
                    dp[i][j] = True
                elif l == 1:
                    dp[i][j] = (s[i] == s[j])
                else:
                    dp[i][j] = (dp[i + 1][j - 1] and s[i] == s[j])
             # j - i +1 = i+l - i +1 = l + 1
                if dp[i][j] and l + 1 > len(ans):
                    ans = s[i:j+1]
        return ans

/**
 * This reference program is provided by @jiuzhang.com
 * Copyright is reserved. Please indicate the source for forwarding
 */

class Solution:
    def longestPalindrome(self, s):
        # write your code here
        # dp 算法班版本
        if not s:
            return ""
        
        # state dp[i][j]代表i到j间的字符是否是回文
        n = len(s)
        dp = [[False] * n for _ in range(n)]
        
        # initialize 单字符和相邻相等字符初始化
        longest, start, end = 1, 0, 0
        for i in range(n):
            dp[i][i] = True
        for i in range(n-1):
            if s[i] == s[i+1]:
                dp[i][i+1] = True
                longest = 2
                start, end = i, i+1 
            
        # function
        for length in range(3, n+1):
            for i in range(n - length + 1):
                j = i + length - 1 
                dp[i][j] = s[i] == s[j] and dp[i + 1][j - 1]
                if dp[i][j] and length > longest:
                    longest = length
                    start, end = i, j
                    
        return s[start:end + 1]

=====================================

======================================

2020-2021学年第二学期移动19级《通信仿真》期末考试试题：

1.采用向量化编程或者for循环，实现如下要求。（15分）

（1）采用随机函数randn()生成一个8*8的随机矩阵A，假设x为A中的任意一个元素，采用逻辑索引等方法找出A中所有满足：-0.5<x<0.5的元素，把这些元素给y。

（2）求出数组y的元素的数目。

（3）把A中满足（1）中要求的元素替换成0，然后输出最新的A；

A=randn(8)

loc=(A>-0.5)&(A<0.5)

y=A(loc)

n=numel(y)

A(loc)=0

2.数组基础操作     （20分）

（1）用magic函数生成一个3*3的魔方矩阵A。

（2）采用randn（）生成一个3*3的的随机矩阵B；

（3）计算C=A+B，并计算C的点2次幂，既D=C.^2；

（4）把A和B水平连接为一个3*6的矩阵E，并求E的转置矩阵F。

（5）求出矩阵E所有元素之和，以及E的所有元素的平均值。

A=magic(3)

B=randn(3)

C=A+B

D=C.^2

E=cat(2,A,B)  %或者 E=[A,B]

F=E'

s=sum(E(:))

m=mean(E(:))

3.求1000-9999之间的全部4位数的水仙花数。（15分）

四位数水仙花数是指：一个四位数，其各位数字4方和等于该数本身。

例如： 1^4 + 6^4 + 3^4 + 4^4 = 1634.那么1634就是一个四位数的水仙花数。

for k=1000:9999

      s=num2str(k);

      n1=str2num(s(1));

      n2=str2num(s(2));

      n3=str2num(s(3));

      n4=str2num(s(4));

      if n1^4+n2^4+n3^4+n4^4==k

         fprintf('找到一个4位的水仙花数：%d\n',k)

      end

end

4.采用循环或向量化编程实现如下要求。（15分）

要求：给两个数组A和B，编程判断B是否是A的子集；（如果B中所有元素都在A中，则称B为A的子集）；

如:  A=[1 3 5 7 9 11]; B=[5 9 3 7]; 则输出“B是A的子集‘；

如： A=[1 3 5 7 9 11]; B=[ 7 9  14]; 则输出“B不是A的子集‘；

A=[1 3 5 7 9 11 5];

B=[5 9 3 7 ];

L=length(B);

s=0;

for k=B

      temp=(A==k);      %如k=5时，temp=[0 0 1 0 0 0 1]

      if sum(temp)>=1  %如果k在A中出现至少1次，即temp中1的个数大于等于1个。

          s=s+1;               %计数器加1

      end

end

if  s==L                        %如果计数器的值和B的长度L相等

    fprintf('B是A的子集\n')

else 

    fprintf('B不是A的子集\n')

end

5.画图          （15分）

x=0:0.01:15;

y1=cos(x).*sin(30*x).*exp(-x/6);

y2=sin(x-8)./(x-8);

plot(x,y1,x,y2)

grid on

title('电压随时间运动关系图')

xlabel('时间（s）');

ylabel('振幅（V）')

6.编程实现月份天数的输出。（20分）

需要满足以下要求。

要求：先用两次input函数，让对方分别输入年份和月份两个数字。然后根据年份以及月份的对应情况，按照以下规则，用fprintf函数输出该月的天数。

规则1： 如果月份为1,3,5,7,8,10,12这些月份，输出天数为31天；

规则2：如果月份为4,6,9,11这些月份，输出天数为30天；

规则3：对于2月份，如果年份为闰年，则2月份天数为29天；如果年份为非闰年（平年），则2月份的天数为28天。

提示1：闰年分为普通闰年和世纪闰年。1、普通闰年：公历年份是4的倍数的，且不是100的倍数，为普通闰年。（如2004、2020年就是闰年）；2、世纪闰年：公历年份是整百数的，必须是400的倍数才是世纪闰年（如，2000年是世纪闰年，而1900年既不是普通闰年也不是世纪闰年，既1900年是平年）

提示2：可以采用switch- case以及if语句完成程序主体；其中判断年份是否为闰年时需要与运算或运算，以及mod()函数。

year     = input('请输入年份：');
month = input('请输入月份：');;
switch month
    case {1,3,5,7,8,10,12}       % 一三五七八十腊，三十一天永不差
        days = 31;
    case {4,6,9,11}                 % 四六九冬三十日
        days = 30;
    case 2                              % 二月需要判断是否为闰年
        if (mod(year,4) == 0 && mod(year,100) ~= 0) || (mod(year,400) == 0)
            days = 29;
        else
            days = 28;
        end
end

fprintf('%d年%d月有%d天。\n',year,month,days )

2000NOIP提高组（全解）

https://www.cnblogs.com/lonely-wind-/p/13227825.html

https://www.cnblogs.com/lonely-wind-/p/13227922.html

https://www.cnblogs.com/lonely-wind-/p/13053965.html

动态规划类题目：（DP+大整数）

（DFS+暴力）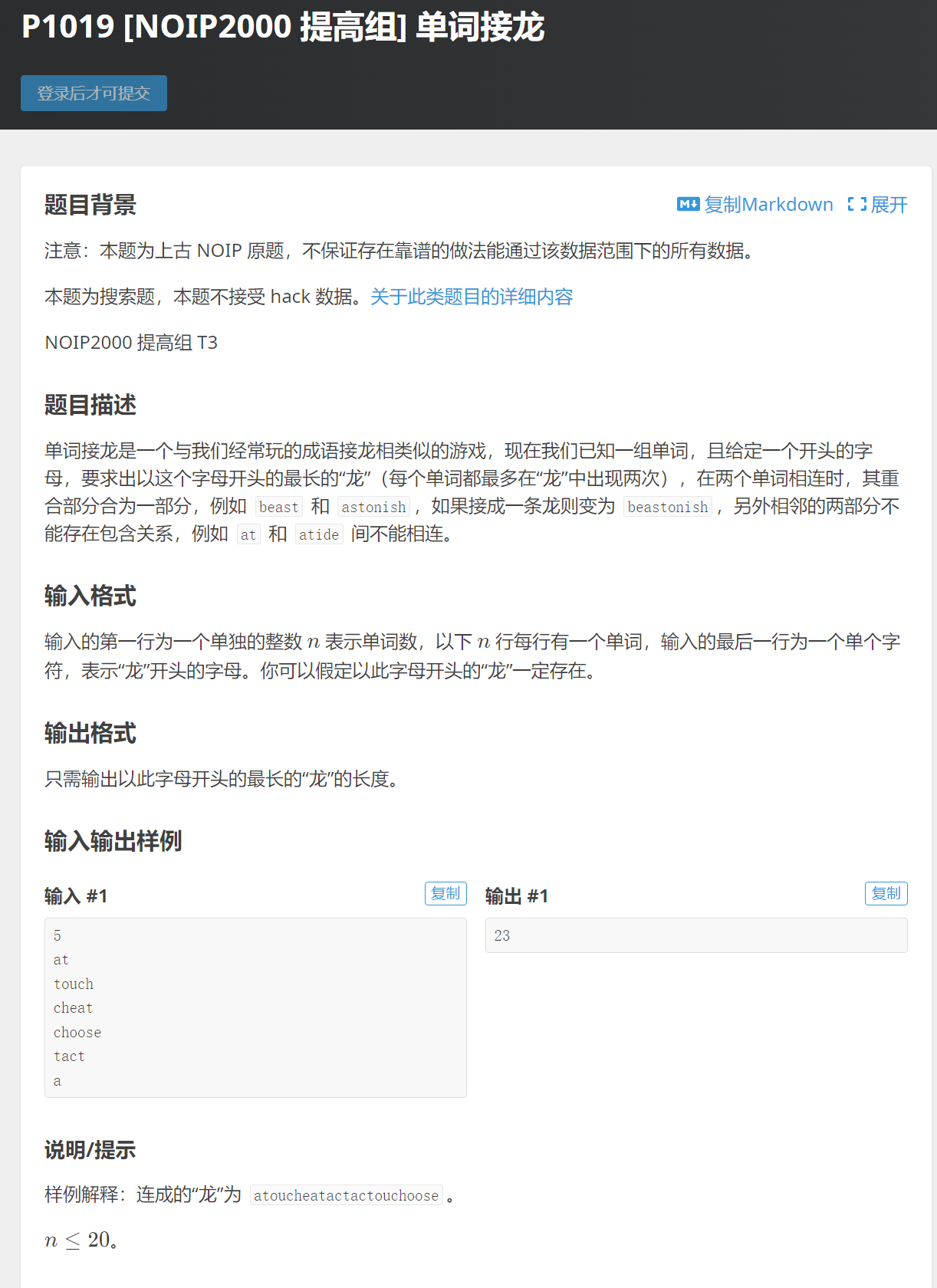           

（DP）

进制转换（负进制的处理）