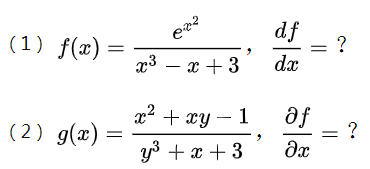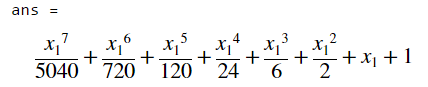MATLAB的符号运算基础            

    在数学运算中，运算的结果如果是一个数值，可以称这类运算为数值运算；如果运算结果为表达式，在MATLAB中称为符号运算，符号计算是对未赋值的符号对象(可以是常数、变量、表达式)进行运算和处理。MATLAB具有符号数学工具箱(SymbolicMath Toolbox)，将符号运算结合到MATLAB的数值运算环境。

符号运算常用函数：

syms     sym()    expand(f)      simplify(f)     factor(f)     collect(f) 

finverse(f, x)     subs(f,x,x0)    solve(eq1,eq2,x,y)    fplot(f,x)    fsurf(z)

limit(f,x,x0)     diff(f,x,n)      int(f,x,a,b)    symsum(s,x,n1,n2)     taylor(f)

(一) 符号变量建立符号变量和符号常数

  建立符号变量的方法有两种 : 应用sym与syms函数，通常应用sym建立符号表达式，应用syms同时定义多个符号变量。

(1)函数：sym与syms

函数：sym（‘表达式或变量’）

sym函数用于建立单个符号对象，其常用调用格式为：符号对象名=sym(A)，将由A来建立符号对象。其中，A可以是一个数值常量、数值矩阵或数值表达式（不加单引号），此时符号对象为一个符号常量；A也可以是一个变量名（加单引号），这时符号对象为一个符号变量。

符号表达式的四则运算与数值运算一样，用+、-、*、/运算符实现，其运算结果依然是一个符号表达式(符号变量的传染性)。

>> x=sym(2)      %相当于把符号‘2’赋给了符号变量x.

x =

2

>> y=10*x-x^2-1

y =

15

>> x1=sym('a');   %相当于把符号‘a’赋给了符号变量x1.

>> y1=sym('b');

>> z=sqrt(x1^2+y1^2)-10

z =

(a^2 + b^2)^(1/2) - 10

>> whos

  Name      Size            Bytes  Class    Attributes

  x            1x1                 8      sym                

  x1          1x1                 8      sym                

  y            1x1                 8      sym                

  y1          1x1                 8      sym                

  z            1x1                 8      sym     

 

%通过sym函数建立符号常量数组！

>> d=sym( [1:10] )

d =

[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

>> f=sym([1,3,5 ; 2,4,6])  %通过sym函数建立符号常量矩阵！

f =

[ 1, 3, 5]

[ 2, 4, 6]

函数：syms        功能：定义多个符号变量

 语法：syms  Var1 Var2 ……Varn

 说明：函数定义符号变量var1，var2，……，Varn等。在用这种格式定义符号变量时无需在变量名上加字符分解符（‘’），变量间用空格而不要用逗号分隔，要用空格来分隔。

例2：应用syms函数定义符号变量

syms x y          %同时定义x，y为符号变量  
A = [sin(x)  sin(y) ; cos(x)  cos(y)]

（2）创建符号数字:

使用sym函数可以创建符号数字.使用符号数字可以精确地保存无理数,不会产生误差.

sym(1/3)     % 得到 1/3
1/3              % 得到 0.3333

将无理数保存为符号数字可以避免将其转换为浮点数的误差:

使用符号数字计算$sin(pi)$

sin(sym(pi))     % 得到 0
sin(pi)              % 得到 1.2246e-16

注意：符号运算的精确值可以达到50万位，远远高于数值计算的精度！

所以当需要进行超大数的运算的时候，尽量采用符号运算。

如，要算2021^2021：

直接double类型数值计算：

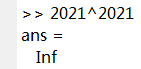，算不出！！

再来看采用符号计算的效果：

再比如，计算1000的阶乘：

直接用factorial(1000)，数值计算只能显示无穷大。

%采用符号计算，方法1：

expand( factorial(sym(1000)) )

%采用符号计算，方法2：

syms n
n=sym(1:1000);
prod(n)

%斐波那契数列求解：

a=sym([1,1])

for  n=3:300

      a(n)=a(n-1)+a(n-2);

end

a(300)

ans =

222232244629420445529739893461909967206666939096499764990979600

如果采用数值型来计算，比如:

a(1)=1,a(2)=1;

for n=3:300

    a(n)=a(n-1)+a(n-2);

end

a(300)

则，无法计算这么大的数字。

练习：创建一个10*10的希尔伯特矩阵

z=sym(zeros(10,10))

for n=1:10

     for m=1:10

         z(n,m)=1/(n+m-1);

     end

end

z

（3）创建符号变量

使用sym和syms可以创建符号变量,区别在于:

sym每次只能创建一个符号变量, 而syms一次可以创建多个符号变量.

as = sym('a');      %定义符号变量a,下同  
bs = sym('b'); cs = sym('c'); ds = sym('d'); %至此定义了4个符号变量  
w = 10; x = 5; y = -8; z = 11;    
A = [as,bs;cs,ds]    %建立符号矩阵A  
B = [w,x;y,z]        %建立数值矩阵B  
C = det(A)           %计算符号矩阵A的行列式  
D = det(B)           %建立数值矩阵B的行列式


A =
    [ a, b]
    [ c, d]
B =
    10     5
    -8    11
C =
    a*d - b*c
D =
    150

若所指定的符号变量已存在,sym不会保留其原有的值,而syms会清空其值.

syms x y
f = x+y;    % 隐式创建符号变量f,即f = x + y

syms x y
f = x+y;    % 隐式创建符号变量f,即f = f

使用sym可以创建符号变量矩阵.

A = sym('a', [2 5])   % 创建一个2*5的符号变量矩阵

得到的输出如下:

A =
[ a1_1, a1_2, a1_3, a1_4, a1_5]
[ a2_1, a2_2, a2_3, a2_4, a2_5]

联合使用sym和syms可以快速创建一系列带下标的变量

clear all
syms(sym('a', [1 5]))
whos

得到输出如下:

   Name      Size            Bytes  Class    Attributes
  a1        1x1                 8   sym                
  a2        1x1                 8   sym                
  a3        1x1                 8   sym                
  a4        1x1                 8   sym                
  a5        1x1                 8   sym

（4）符号多项式与多项式系数向量之间的转换：
           符号多项式转换为多项式系数向量：p=sym2poly(s)
          

 多项式系数向量转换为符号多项式：s=ploy2sum()  

（5）符号变量和字符型以及数值型之间的相互转换：

符号型转字符型：使用函数char

>> z1=sym(88)^88;

z2=char(z1)

z2 =

 '1301592834942972055182648307417315364538725075960067827915311484722452340966317215805106820959190833309704934346517741237438752456673499160125624414995891111204155079786496'

>> z3=str2num(z2)

z3 =

  1.3016e+171

符号型转数值型：

方法1：r = double(S) 

例：r = double(sym((1+sqrt(5))/2)) 

综合实例：

>>  s0=123456789      %生成double型

s0 =

   123456789

>> s1=num2str(s0)    %double型转换为字符串

s1 =

    '123456789'

>> s2=sym(s1)          %字符串转为符号型

s2 =

123456789

>> s3=sym(s0)          %double型转为符号型

s3 =

123456789

>> s4=str2num(s1)    %字符号型转为数值型

s4 =

   123456789

>> s5=double(s2)      %符号型转为数值

s5 =

   123456789

>> whos

  Name      Size            Bytes  Class     Attributes

  s0        1x1                 8        double              

  s1        1x9                18       char                

  s2        1x1                 8        sym                 

  s3        1x1                 8        sym                 

  s4        1x1                 8        double              

  s5        1x1                 8        double         

(二)基本的符号运算

1.基本符号运算函数

在MATLAB中,有很多应用于符号运算的函数，常用的函数如下表所示：

2.符号表达式基本运算

 （1）符号表达式的四则运算

syms x y z;              %定义x,y,z为符号变量  
f1 = 2*x+x^2*x-5*x+x^3  
f2 = 2*x/(5*x)  
f3 = (x+y)*(x-y)

      （2）符号表达式的化简

使用simplify()函数可以化简符号表达式.

syms x;

f = 2*(x-1)/(x^2+2*x-3)    %输入表达式 

F = factor(f)                       %对符号表达式f进行因式分解 

F =

[ 2, 1/(x + 3)]

syms x a b c

simplify( sin(x)^2 + cos(x)^2 )       % 得到 1
simplify( exp(c*log(sqrt(a+b))) )     % 得到 (a + b)^(c/2)

符号矩阵也是一种符号表达式，所以符号表达式运算都可以在矩阵意义下进行。
注意：这些函数作用于符号矩阵时，是分别作用于矩阵的每一个元素。

表达式化简的标准是不确定的,下面三个函数分别按照不同标准化简表达式:

• expand()函数可以展开表达式

  syms x
  
  f = (x ^2- 1)*(x^4 + x^3 + x^2 + x + 1)*(x^4 - x^3 + x^2 - x + 1);
  expand(f)    % 得到 x^10 - 1
  

• factor()函数可以分解因式

  syms x
  
  g = x^3 + 6*x^2 + 11*x + 6;
  factor(g)       % 得到 (x + 3)*(x + 2)*(x + 1)
  

• horner()函数可以将多项式变为嵌套形式

  syms x
  h = x^5 + x^4 + x^3 + x^2 + x;
  horner(h)       % 得到 x*(x*(x*(x*(x + 1) + 1) + 1) + 1)

3、符号表达式的代入subs（）使用subs(expr, old, new)函数可以将符号表达式expr中的old替换为new.

syms x
f = 2*x^2 - 3*x + 1;
subs(f, 1/3)                   % 得到 2/9

>> syms x y
>> f = x^2*y + 5*x*sqrt(y);
>> d1=subs(f, x, 3)       % 代入x的值
d1 =9*y + 15*y^(1/2)

>> d2=subs(d1, y, 2)     % 代入y的值
d2 =15*2^(1/2) + 18

>> vpa(d2)
ans =39.213203435596425732025330863145

4.符号多项式以及求根roots

syms a b c

p=[a ,b,c]

roots(p)

4、 符号方程的解析解solve（）

使用solve(eqn,var)和solve(eqns,vars)可以求取方程式的解析解.

符号运算中变量的确定:

如果没有明确指定自变量，MATLAB将按以下原则确定主变量并对其进行相应运算：

寻找除了i、j之外，在字母顺序上最接近x的小写字母。

若表达式中有两个符号变量与x的距离相等，则ASCII码大者优先。

symvar()函数可以用于查找一个符号表达式中的符号变量，函数的调用格式为：symvar(s,n)。函数返回符号符号表达式s中的n个符号变量。因此，可以用symvar(s, 1)查找表达式s的主变量。

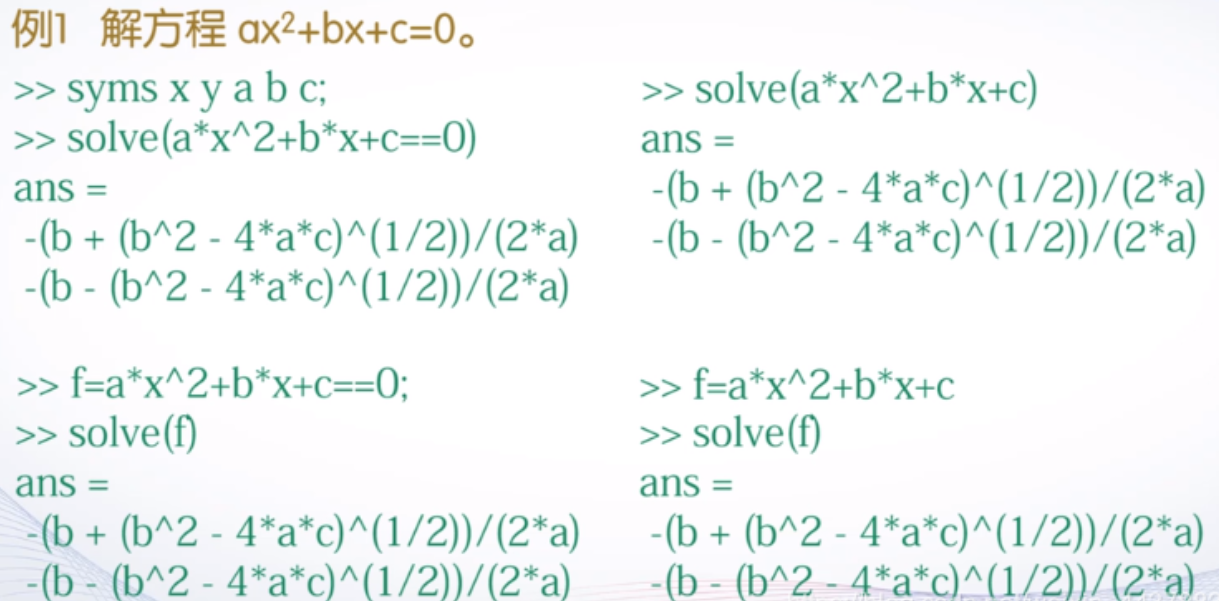
4.1 解单变量方程

使用==定义一个方程,并对其调用solve函数求解.

syms x y a b r
solve((x - a) ^ 2 + (y - b) ^ 2 - r ^ 2,x)

ans =
 a + (b + r - y)^(1/2)*(r - b + y)^(1/2)
 a - (b + r - y)^(1/2)*(r - b + y)^(1/2)

若不指定==符号右边的值,则默认等式右边为0.

syms x
eqn = x^3 - 6*x^2 + 11*x - 6;
solve(eqn)     % 得到 [1 2 3]

4.2 解多变量方程

对于多变量方程,我们需要指定针对哪个变量进行求解.

syms x y
eqn = [6*x^2 - 6*x^2*y + x*y^2 - x*y + y^3 - y^2 == 0];
solve(eqn, y)    % 得到 [1, 2*x, -3*x]

4.3 解方程组

向solve()函数传入方程组可以解方程.

syms u v
%写法1：
eqns = [2*u + v == 0, u - v == 1];
S = solve(eqns,u,v)    %解S为结构体类型
%写法2：
%eqn1 = 2*u + v == 0;
%eqn2 = u - v == 1;
%S = solve(eqn1,eqn2,u,v)    %解S为结构体类型

%运行上述代码得到:
S = 
  包含以下字段的 struct:

    u: [1×1 sym]
    v: [1×1 sym]
>> S.u
ans =
1/3
>> S.v
ans =
-2/3

可以通过变量名索引方程的解,并可以将该解代入其他表达式中.

S.u;       % 得到 1/3
S.v;       % 得到 -2/3
subs(3*v + u, S);  % 得到 -3/5

运行后，得到方程的解a，a是一个结构体。

%如果方程中存在多个符号变量，怎么解？

>> syms x a b

>> eq=a*x^2-b;

>> s1=solve(eq)   %如果有x这个字母作为符号变量，则首先默认它是需要求的未知量

s1 =

  b^(1/2)/a^(1/2)

 -b^(1/2)/a^(1/2)

>> s2=solve(eq,a)  %把a当初未知量求解。

s2 =

b/x^2

>> s3=solve(eq,b)    %把b当初未知量求解。

s3 =

a*x^2

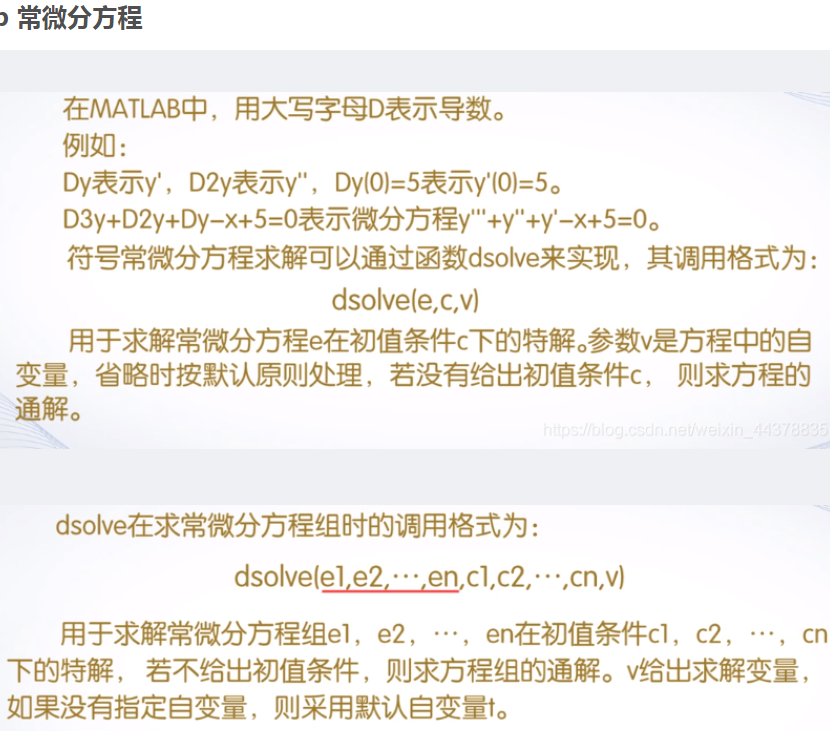
4.4常微分方程 dsolve()

close all;clc;

hold on;

fimplicit(@(x,y)(x-2).^2+(y-3+2.*x).^2-5,[1.5,5 -8,3]);

fimplicit(@(x,y)2.*(x-3).^2+(y./3).^2-4,[1.5,5 -8,3]);

hold off;

% 将两个椭圆和求得的交点绘制在同一图形中

fun=@(x)[(x(1)-2).^2+(x(2)-3+2.*x(1)).^2-5,2.*(x(1)-3).^2+(x(2)./3).^2-4];

[x,f,h]=fsolve(fun,[2,2])

[x,f,h]=fsolve(fun,[3.5,-5])

[x,f,h]=fsolve(fun,[4,-4])

hold on;

plot([1.6581 1.7362 3.4829 4.0287],[1.8936 -2.6929 -5.6394 -4.1171],'ro');

fimplicit(@(x,y)(x-2).^2+(y-3+2.*x).^2-5);

fimplicit(@(x,y)2.*(x-3).^2+(y./3).^2-4);

hold off;

5、符号表达式的微积分运算

5.1 符号表达式的极限limit()

limit(F, x, a)：求当时，符号表达式F的极限。

limit(F,a)：符号表达式F采用默认自变量（可由函数findsym求得），该函数求F的自  变量趋于a时的极限值。

limit(F)：符号表达式采用默认变量，并以a=0作为自变量的趋近值。

limit(F,x,a,'right') 或 limit(F,x,a,'left')：分别求符号表达式的左极限和右极限。

>> syms x

>> f1=(cos(x)+sin(x)-x)/x

>> limit (f1 ,x ,inf) 

ans =-1

>> limit(f1,x,-inf)

ans = -1

 

>> limit(f1,x,0)

ans = NaN

 

>> f2=(sin(x)-x)/x;

>> limit(f2,x,0,'right')

 ans =0

 

>> limit(f2,x,0,'left') 

ans = 0

练习：利用符号求极限方式，计算下列两个极限

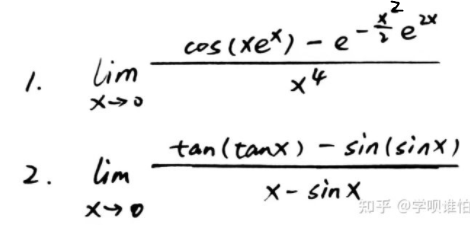
5.2 符号表达式的微积分运算:diff函数

函数diff可以完成一元或多元函数任意阶数的微分。

diff函数语法：

diff(S ,'v')：将符号“ v ”视作变量，对符号表达式或者符号矩阵求取微分。

diff(S , n)：将S中的默认变量进行n阶微分运算，其中默认变量可用findsym函数确定。

diff(S,'v',n)：将符号“ v ”视作变量，对符号表达式或矩阵S进行n阶微分运算。

>> syms x y z;

>> f1=exp(x*sin(y))+log(z);

>> diff(f1 , x , 1 )

ans = exp(x*sin(y))*sin(y)

>> diff(f1,y)

ans =x*exp(x*sin(y))*cos(y) 

>> diff(f1,z)

ans = 1/z 

>> diff(f1,x,2)

ans =exp(x*sin(y))*sin(y)^2

>> syms a b c x;

expr = a*x^2 + b*x + c;

>> diff(expr, a)

ans = x^2

>> diff(expr, b)

ans = x

>> diff(expr, x)

ans =b + 2*a*x

>> diff(expr, x, 2)

ans =2*a

syms x y
%% 第一题
y1 = (exp(x^2)) / (x^3-x+3)
dy1 = diff(y1)         

%% 第二题
y2 = (x^2+x*y-1)/(y^3+x+3)
dy2=diff(y2,x)  

多元偏导数：

求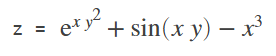的多元偏导数

syms x y

z=exp(x*y^2)*sin(x*y)-x^3;

fxy=diff(z,x,y)   %先求x偏导，再求y偏导

fyx=diff(z,y,x)   %先求y偏导，再求x偏导

练习：

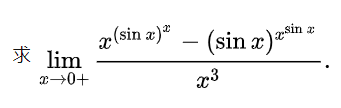
5.3 jacobian函数

对于自变量的个数多于一个的符号矩阵，微分为Jocabian矩阵，采用功能函数Jacobian实现。

R=jacobian(w,v)：其中w是一个符号列向量，v是指定进行变换的变量所组成的行向量。（第一个参数必须是列向量，第二个参数必须是行向量）

>> f2=sym('[x^2+y^2 ; y*z]')

f2 =

 x^2 + y^2

       y*z

>> J=jacobian(f2,[x,y])

J =

[ 2*x, 2*y]

[   0,   z]

5.4 符号表达式的积分 int()

R=int(S)：用默认变量求符号表达式S的不定积分，默认变量可用函数findsym确定。

R=int(S,v)：用符号标量v作为变量求符号表达式S的不定积分。

R=int(S,a,b)：符号表达式采用默认变量，该函数求默认变量从a到b时符号表达式S的定积分值。如果S是符号矩阵，那么积分将对各个元素分别进行。

R=int(S,v,a,b)：用符号标量v作为变量，求当v从a变到b时，符号表达式S的定积分值。

>> syms x y

>> f1=x+x^-1 ;

>> int(f1)

ans =log(x) + x^2/2 

>> f2 =1/(x*y) + x*y 

>> int(f2 , y)

ans =log(y)/x + (x*y^2)/2

s=int(f1, 1, 2)

s2=vpa(s)

s3=eval(s)     %eval的作用见附录

class(s2)       %查看两种方式显示具体值的数值的类型。

class(s3)

s =log(2) + 3/2

s2 =2.1931471805599453094172321214582

s3 =2.1931

ans ='sym'

ans = 'double'

>> int(f2, y, 1 ,2)

ans =(3*x)/2 + log(2)/x

练习：

syms x;
 f = (x^2-x+1) / (x+3);
Fint = int(f,x,[0 10])

Fint =
log(302875106592253/1594323) + 10

，

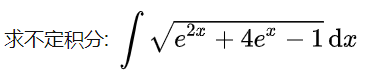
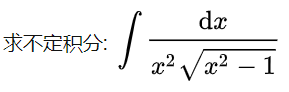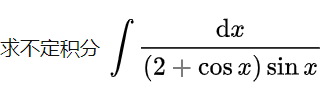
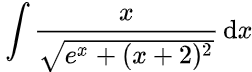
5.5 符号表达式的级数求和: symsum(expr, n, [a b])

r=symsum(s,a,b)：求符号s表达式中默认变量从a变到b时的有限和。

symsum(s,x,a,b)：求符号s表达式中变量x从a变到b时的有限和。

>> syms x y n

>> f1=x^2; 

>> symsum(f1,0,n-1)

ans =(n*(2*n - 1)*(n - 1))/6

>> f2=sym('x^n')

f2 =x^n

>> symsum(f2,n,0,inf)

ans =piecewise([1 <= x, Inf], [abs(x) < 1, -1/(x - 1)])

syms k x

symsum(k^2, k)   % 得到 k^3/3 - k^2/2 + k/6
symsum(k^2, k, [0 10])           % 得到 385
symsum(x^k/factorial(k),k,1,Inf)  % 得到 exp(x) - 1

用以下公式计算圆周率：

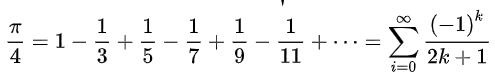
5.6  符号表达式的泰勒级数

r=taylor( f )：f是符号表达式，其变量采用默认变量，该函数返回f在变量等于0处作5阶泰勒展开时的展开式。

r=taylor(f , n ,x)：符号表达式f以符号标量x作为自变量，返回f的n-1阶麦克劳林级数(即在x=0 处的泰勒展开)展开式。

r=taylor(f,n,x,a)：返回符号表达式f在x=a处作n-1阶泰勒展开时的展开式。

>> syms  x y

>> f1=sin(x)/(sin(x) + 2)

>> taylor(f1)

ans = - (13*x^5)/480 + x^4/48 + x^3/24 - x^2/4 + x/2

syms x1

taylor(exp(x1),x1,0,'Order',8)

5.7 fminbnd 和 fminsearch 函数求极值点的确切位置

fun=@(x)abs(x.^3-x.^2-x-2);

fplot(fun)

grid on;

[x,f]=fminbnd(fun,0,2)

[x,f]=fminbnd(fun,1,3)

[x,f]=fminsearch(fun,1)

[x,f]=fminsearch(fun,2)

2）假定某天的气温变化记录如下：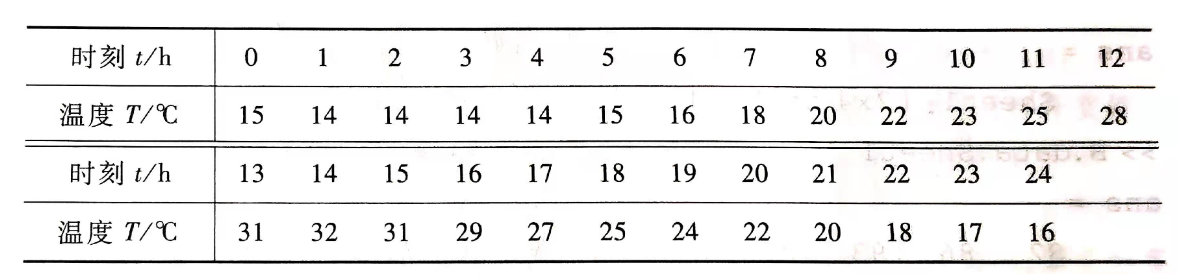

试用最小二乘法找出这一天的气温变化规律. 考虑下列类型函数，作图比较结果，并计算误差平方和

1）三次函数

x=0:24;

y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];

fun1=@(c,x)c(1)*x.^3+c(2)*x.^2+c(3)*x+c(4);

[c1,Q1]=lsqcurvefit(fun1,[0,0,0,0],x,y)

z=c1(1)*x.^3+c1(2)*x.^2-c1(3)*x+c1(4);

plot(x,y,'ro',x,z,'b')

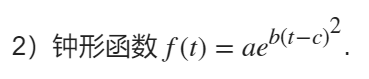
x=0:24;

y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];

fun2=@(c,x)c(1)*exp(c(2)*(x-c(3)).^2);

[c2,Q2]=lsqcurvefit(fun2,[0,0,0],x,y)

z=c2(1)*exp(c2(2)*(x-c2(3)).^2);

plot(x,y,'ro',x,z,'b')

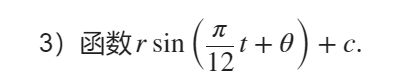
x=0:24;

y=[15 14 14 14 14 15 16 18 20 22 23 25 28 31 32 31 29 27 25 24 22 20 18 17 16];

fun3=@(c,x)c(1)*sin(pi/12*x+c(2))+c(3);

[c3,Q3]=lsqcurvefit(fun3,[0,0,0],x,y)

z=c3(1)*sin(pi/12*x+c3(2))+c3(3);

plot(x,y,'ro',x,z,'b')

（三）符号函数的图像绘制

可以对符号表达式绘制图像,常用的绘图函数如下:

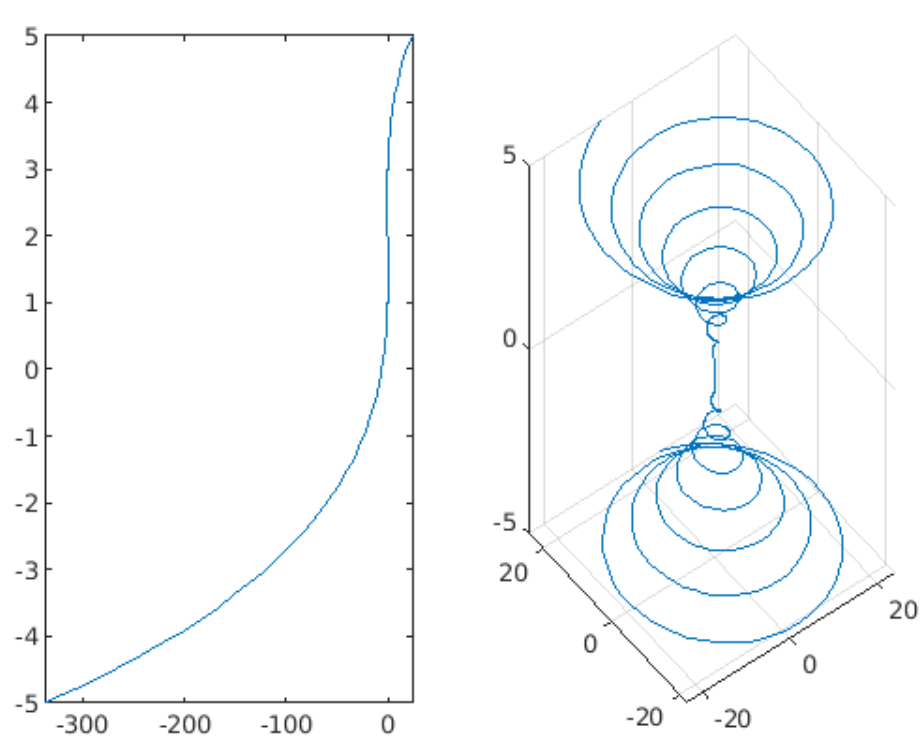
下面例子展示二维和三维线图像的绘制

subplot(1, 2, 1)
syms x
f = x^3 - 6*x^2 + 11*x - 6;
fplot(f, x)

subplot(1, 2, 2)
syms t
fplot3(t^2*sin(10*t), t^2*cos(10*t), t)

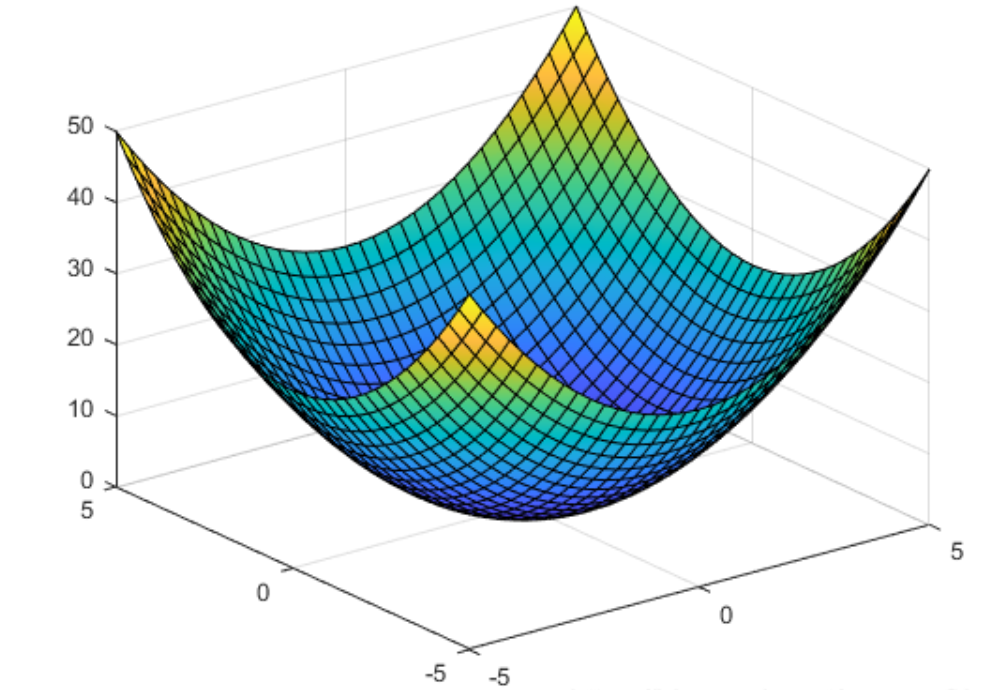
下面例子演示三维面的绘制

syms x y
fsurf(x^2 + y^2)

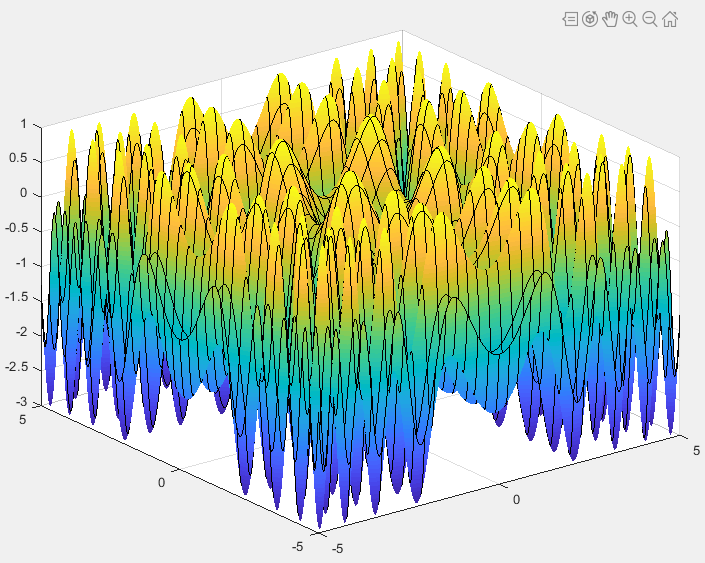
sym x y

fsurf(sin(x^2 )+ sin(y^2)-1)

1. 下面例子演示隐含函数关系图像的绘制

   syms x y
   eqn = (x^2 + y^2)^4 == (x^2 - y^2)^2;
   fimplicit(eqn, [-1 1])
   

   
   

=====================================

作业：上机实操例子

   
    %符号变量
        a = sym('a')
        syms b;
        b
    %符号常量
        c = sym('3');
    
    %符号表达式
        syms x
        f1 = 3*x+6
        f2 = 3*x+6
    %符号四则运算
        fadd1 = f1 + f2
        fsub1 = f1 - f2
        fmu1 = f1*f2
        fdiv = f1 / f2
    
    %符号表达式化简
        syms x y
        s = (x^2+y^2)^2+(x^2-y^2)^2;
        spy = simplify(s); 
    
    %符号表达式和数值的转换
        eval(c)
    %因式分解，展开和合并同类项
        syms a b x y
        f1 = a^3 - b^3;
        factor(f1) %因式分解
    
        f2=(3*x^2+8*y^2)*(-x^2+3*y);
        expand(f2) % 展开
    
        f3=3*x^2+4*x^2+5*x^2*y;
        collect(f3) % 合并同类型
    
    %符号矩阵
            a1 = [x x+y;y y^2] 
            transpose(a1) % 普通转置
            a1' % 共轭转置
    
        %符号函数值的求解
            syms x
            f1 = x^3-9;
            subs(f1,3)
    
        % 符号极限，符号微分，符号积分
            syms x a
            y =sin(x+a);
            limit(y,0)
            y2 = sqrt(1+exp(x));
        
        diff(y2)  % 数值中是求差分，符号计算是求解导数
        diff(y2,2) % 求二重导数
        diff(y2,3)
    
        y3 = (3-x^2)^3; % 不定积分
        int(y3)
    
    % 求定积分
        y4 = abs(1-x);
        int(y4,1,2)
    
    % 符号级数求和、泰勒级数
        syms n
        f = 1/ n^2;
        s1 = symsum(f,n,1,inf) % 无穷级数  
    
    %泰勒展开  
        syms x
        y = (1 + x + x^2) / (1 - x + x^2);
        taylor(y,x,1,'Order',3) % 在x=1处进行taylor展开并且 得到第三项的值
    
    %符号代数方程
        clear 
        syms x
        eval(solve(x+x*exp(x)-10))     %eval的作用见附录
        
    % 方程组
        clear
        syms x y
        [x y] = solve('x+y-98','x^(1/3)+y^(1/3)-2','x,y')
    
        [x y] = solve('1/x^3+1/y^3-28','1/x+1/y-4','x,y')
    
    %符号微分方程
        dsolve('Dy-(x^2+y^2)/x^2/2','y(1)=2','x')
        
=====================================================        
        
syms x
y=x.^3+2*x.^2+2;
d=diff(y)            %求一阶导数
>>d=3*x^2 + 4*x


syms x
syms t
y=x.^3+2*x.^2+2;
q1=int(y)
q2=int(y,1,2)
q3=int(y,'t')
d=diff(y)
d2=diff(y,2)
d3=diff(y,'t')

>> 
q1 = (x*(3*x^3 + 8*x^2 + 24))/12
q2 =125/12 
q3 =t*(x^3 + 2*x^2 + 2)
d =3*x^2 + 4*x
d2 =6*x + 4
d3 =0

应用 
例子一：
clc,clear
syms dt
dv=0.1                        %速度=0.1m/s        %恒速运动
ds=dv*dt
s=int(ds,'dt',0,2)        %求走过的距离

>>s=1/5 

===============================================

选学内容：

1、eval的作用

help eval 将看到matlab自带的说明：
eval Execute string with MATLAB expression. eval(s), where s is a string, causes MATLAB to execute the string as an expression or statement.
翻译一下，就是说eval函数的功能是将字符串转换为matlab可执行语句。通俗而言，比如：
你输入
a='b=1';
会在workspace里看见生成了变量a，a的类型是字符串，字符串的内容是b=1
然后你输入eval(a)
就会看见变量里生成了变量b，b是一个1乘1的double型矩阵，元素的值为1
也就是说，执行eval(a)相当于执行a的内容，相当于执行b=1
如果说for语句可以将数字进行循环，那么eval结合for语句后，则大大提高其循环范围。
比如你要载入一些数据，m1.mat，m2.mat等等一直到m100.mat
普通青年可能会这样写程序
load m1.mat
load m2.mat
然后一直写100行，这显然太笨了！但普通的for语句又无法完成
于是eval函数结合for语句就体现出其价值了
for i=1:100
    eval(['load ' num2str(i) '.mat'])
end
只需要三行！
除此之外，eval还广泛用于人机交互，因为matlab的gui中，get命令得到的str格式的字符
串，通常，会通过str2num将字符串转换为数字，供后续处理。而如果读入的str字符串是
cos，sin之类的指令呢？那么就需要结合eval函数，将字符串转换为指令。

eval函数具有将字符串自动识别并转化为matlab命令的功效。
比如eval('x=1') 可以直接定义变量x，并为之赋值为1，即执行引号内matlab命令。


eval（s）即 把字符串s的内容当作语句来执行
比如：eval_r('a=3*5') 和直接在command 窗口中输入 a=3*5 等效
（注：本文的eval（）都被页面处于安全考虑而自动改成了 eval_r（））

eval 一个经常用到的地方就是 将一些[符号表达式] 转换为 [数值]结果，比如用solve解一个方程得到 ：
syms x
a=solve(x^2+4*x-9=)
a =
     - 13^(1/2) - 2
     13^(1/2) - 2
为了得到直观的小数表示，我们输入 eval(a)就得到：
 ans =
-5.6056
  1.6056
ps：可以试试 eval（'a'）和eval_r（a） ，结果是不一样的，为什么？



1、假如我要对a1,a2,a3,a4,……,a10分别赋予1,4,9，……，100，这时eval就发挥作用了。
for i=1:10
    eval(['a' num2str(i) '=' num2str(i^2)]);
end
k=0;
limit=9;
for n=1:9
    for m=1:limit
        fprintf('%d * %d =-    ',n,m,n*m)
        k=k+1;
        if k==limit
           fprintf('
')
           k=0;  
        end
    end
    limit=limit-1;
end

作业1：

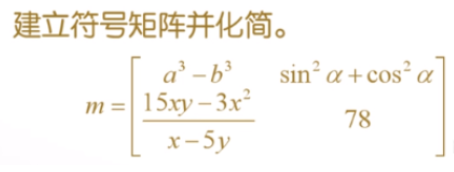
作业2：

作业3：

作业4：

作业5：

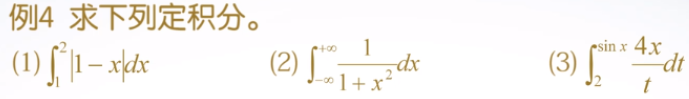
作业6：

作业7：

==============================================

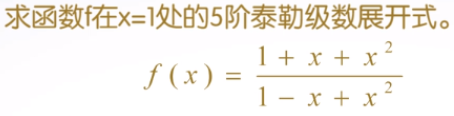
             符号运算 sym与表达式操作总结

1  f = sym(‘符号表达式’) % 定义符号表达式，并将它赋值给变量f

不行用str2sym

2.求反函数 

调用函数：finverse 

函数功能：求得符号函数的反函数 

调用格式：finverse(f, v), 其中f为符号表达式，v是自变量

3.求复合函数 

调用函数：compose 

函数功能：求符号函数的复合函数 

调用格式： 

compose(f, g) 

compose(f, g, z) 

compose(f, g, x, z) 

compose(f, g, x, y, z)

4.表达式替换 

调用函数：subs 

函数功能：表达式替换 

调用格式： 

subs(s) 

subs(s, new) 

subs(s, old, new)

5 极限

调用函数：limit 

调用格式： 

g = limit(f) 

g = limit(f, a) 

g = limit(f, x, a) 

g = limit(f, x, a, ‘left’) 

g = limit(f, x, a, ‘right’)

Note：如果自变量不是x，最好显示说明 

代码示例：

syms h x;

limit((sin(x + h) - sin(x))/h, h, 0)

6 微分

调用函数：diff 

调用格式： 

diff(f) 

diff(f, t) 

diff(f, n) 

diff(f, t, n)

例题：已知f(x) = a*x^2 + b*x + c, 求f(x)的微分 

代码如下：

syms a b c x 

f = a*x^2 + b*x + c

diff(f)

diff(f, 2)

diff(f, a, 2)

diff(diff(f), a)

7 积分

调用函数：int 

调用格式： 

int(f) 

int(f, t) 

int(f, a, b), (a, b为数值式) 

int(f, t, a, b) 

int(f, m, n), (m, n为符号式)

例题：已知f(x) = a*x^2 + b*x + c, 求f(x)的积分 

代码如下：

syms a b c x;

f = a*x^2 + b*x + c

int(f)

int(f, x, 0, 2)

int(f, a)

int(int(f, a), x)

 8 级数

调用函数：symsum, taylor 

调用格式： 

symsum(s, v, a, b) 

taylor(F, v, n)

代码如下：

syms k;

synsum(1/k, k, 1, inf)

symsum(1/(k*(k + 1)), k, 1, inf)

syms x

ou = taylor(sin(x), x, 10);

subs(ou, x, pi/2)

 9 方程求解

调用函数：solve 

调用格式：solve(f1, f2, …, fn, v1, v2, …, vn)

例题：求一元二次方程f(x) = a*x^2 + b*x + c的根 

f = a*x^2 + b*x + c

solve(f) 

syms a 

solve(f, a)//一个为方程，一个为要求的变量

10 微分方程求解

调用函数：dsolve 

调用格式： 

dsolve(f, cond, v) 

dsolve(f1, f2, …, fn, cond1, cond2, …, condn, v1, v2, …, vn) 

dsolve(f1, f2, …, fn)