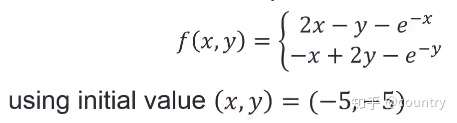Matlab中的数值计算
MATLAB中方程求解内置函数 solve, vpasolve, fsolve, fzero, roots功能和信息概览
求解 函数 | 多项式型 | 非多项式型 | 一维 | 高维 | 符号 | 数值 | 算法 |
| solve | 支持,得到全部符号解 | 若可符号解则得到根 | 支持 | 支持 | 支持 | 当无符号解时 | 符号解方法:利用等式性质得到标准可解函数的方法 基本即模拟人工运算 |
| vpasolve | 支持,得到全部数值解 | (随机初值)得到一个实根 | 支持 | 支持 | 支持 | 未知 | |
| fsolve | 由初值得到一个实根 | 由初值得到一个实根 | 支持 | 支持 | 支持 | 优化方法,即用优化方法求解函数距离零点最近,具体方法为信赖域方法。 包含预处理共轭梯度(PCG)、狗腿(dogleg)算法和Levenberg-Marquardt算法等 | |
| fzero | 由初值得到一个实根 | 由初值得到一个实根 | 支持 | 支持 | 一维解非线性方程方法,二分法、二次反插和割线法的混合运用 具体原理见数值求解非线性方程的二分法、不动点迭代和牛顿法和插值方法 | ||
| roots | 支持,得到全部数值解 | 支持 | 支持 | 特征值方法,即将多项式转化友矩阵(companion matrix) 然后使用求矩阵特征值的算法求得所有解(那是另外一个问题了) |
MATLAB求解方程根的方法:
(1)Analytical Solutions(解析解) solve
(2)Graphical Illustration(图解法)
(3)Numerical Solutions(数值解)fsolve, fzero, roots

1. (符号/数值)解方程(组)函数 solve
官方参考页:Equations and systems solver - MATLAB solve
solve函数语法:
S = solve(eqn,var)
S = solve(eqn,var,Name,Value)
Y = solve(eqns,vars)
Y = solve(eqns,vars,Name,Value)
[y1,...,yN] = solve(eqns,vars)
[y1,...,yN] = solve(eqns,vars,Name,Value)
[y1,...,yN,parameters,conditions] = solve(eqns,vars,'ReturnConditions',true)
S = solve(eqn,var) 求解变量var的方程eqn 。如果未指定var, symvar 函数将确定要为其求解的变量。例如, solve(x + 1 == 2, x)解决等式 x + 1 = 2为x .
例子
S = solve(eqn,var,Name,Value) 使用由一个或多个Name,Value对参数指定的附加选项。
例子
Y = solve(eqns,vars) 解决了方程组eqns的变量vars , 并返回一个结构, 包含解决方案。如果不指定vars, 则solve使用 symvar 查找要解决的变量。在这种情况下, symvar发现的变量数等于等式的个数eqns.
例子
Y = solve(eqns,vars,Name,Value) 使用由一个或多个Name,Value对参数指定的附加选项.
例子
[y1,...,yN] = solve(eqns,vars) 解决了变量vars的eqns方程组。解决方案被分配给y1,...,yN的变量。如果不指定变量, solve使用symvar查找要解决的变量。在这种情况下, symvar发现的变量数等于输出参数的个数N.
[y1,...,yN] = solve(eqns,vars,Name,Value) 使用由一个或多个名称指定的附加选项Name,Value对参数。
例子
[y1,...,yN,parameters,conditions] = solve(eqns,vars,'ReturnConditions',true) 返回指定解决方案中的参数和解决方案条件的附加参数parameters和conditions。
S = solve(eqn,var):解出关于变量var的方程eqn,如果不指定var,则由symvar函数决定要解的变量。solve(x + 1 == 2, x) 解出x的方程x + 1 = 2。
通过solve()求解出来的解也是sym类型,不是double类型的数值。
C = symvar(expr) 搜索表达式 expr,查找除 i、j、pi、inf、nan、eps 和公共函数之外的标识符。这些标识符是表达式中变量的名称。symvar 返回搜索到的标识符。如果 symvar 找不到标识符,则 C 是一个空的元胞数组。
较新版本matlab删除了对字符向量或字符串输入的支持。需要先使用 syms 来声明sym变量,然后将 solve('2*x == 1','x') 这样的输入替换为 solve(2*x == 1,x) 。
①求解单个一元方程的数值解
syms x;
x0 = double(solve(x +2 - exp(x),x));
求x+2 = exp(x)的解,结果用double显示.
使用过程中,也可以写作x+2 == exp(x),注意是‘==’.
另外,若有多个解,该函数只返回一个的解.
②求解含有符号变量方程的解
syms x a b c;
x0 = solve(a*x^2+b*x+c , x);
可以求得两个解.
③求解方程组
syms x y z;
e1 = 2*x - y +z;
e2 = x + y - 6;
e3 = z^2 +2*y;
[x0,y0,z0] = solve(e1,e2,e3,x,y,z);
double([x0,y0,z0])
可以返回多个解,注意不能直接solve进行double转换.
(1)
syms x
y =cos(x) ^ 2 - sin(x) ^ 2
solve(y,x) %y是equation
ans =
pi/4
(2)
syms x
y =cos(x) ^ 2 + sin(x) ^ 2
solve(y,x) %y是equation
ans =
Empty sym: 0-by-1 %说明,该方程本身无解,或者该方程过于复杂。
solve 函数的局限性:
对于非多项式方程,只能求出一个解
对于稍许复杂的方程,求解结果出现很大误差
求解复杂的多项式方程时,可能会产生错误的求解结果
求解复杂的多项式方程时,可能无法求解,且非常耗时
求解超越方程时,只能返回一个解;
求解超越方程时,可能返回错误解;
fsolve函数
fsolve函数语法:
x = fsolve(fun,x0)
[x,fval,exitflag] = fsolve(fun,x0,options)
fun: 函数,用于定义方程(组)
x0: 计算初值
x: 求解结果(方程的根)
fval: 将求解结果x 带入方程(组) fun,对应的值,即fun(x),既精度!
exitflag: 返回方程组求解结果的状态(详见help 文档)
options: 方程的求解设置
MATLAB fsolve函数总结
fsolve可以求解方程(组) 的实数根和复数根
fsolve采用迭代的数值算法,速度快
给定不同的初值,可以求得不同的根(局部寻根)
初值给的不好,可能导致求解失败
关于初值如何给定的问题?
a) 通过图解法,大概观察根的个数,并粗略地估计出根的值,用做fsolve的初值
b) 根据方程组中变量的实际意义,合适地给出初值。例如,时间/ 长度/ 质量等物理量,应该大于0
c) 通过更多的练习和经验积累,自然会见多识广
fsolve 是数值求解,solve是符号求解。具体到调用语法上,fsolve要求输入是一个函数句柄,solve则是符号表达式或者string定义的表达式
如果非要找出个规律的话,只能说很多带 f 前缀的函数是数值求解,需要接受的是函数句柄,如:fsolve、fzero、fminsearch 等
总结:
尽量避免使用solve函数
尽可能使用fsolve求解数值解
fzero与fsolve解方程的区别? “二者主要面向的对象不同,fzero 是求一元方程的,fsolve主要是求多元方程组(当然也包括一元方程)。在求一元方程上,从用户使用的角度并无什么区别,只是内核算法不同。fzero 求解一元方程往往更容易些,因为他不仅支持提供初值的搜索,还可以在一个区间上搜索,但是他不支持多元方程。
求一个区间内所有的零点,只能提供不同的初值依次求解”
对于复杂的方程,先作图得到解的分布情况然后再确定初值应该会比较靠谱吧,纯靠猜感觉很难得到自己想要的解。
solve 是基本的用于符号解方程的内置函数,返回类型为符号变量矩阵( sym)。当无法符号求解时,抛出警告并输出一个数值解。基本形式为:
1 | solve(eqn, var, Name, Val); % eqn为符号表达式/符号变量/符号表达式的函数句柄, var为未知量; Name为附加要求,Val为其值 |
可以用solve解一维方程。对于多项式,solve可以返回其所有值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
syms x exp1; % 定义符号变量 x, exp1;
solve(exp1 == 0, x) % 传入一个包含符号表达式的等式,x为所要求的变量solve(exp1, x) % 传入一个符号表达式,函数默认求其零点solve(func1(x), x) % 传入参数func1(x)等价于传入了符号表达式,和输入b完全一样solve(func1(x) == 0, x) % 这句话和上式完全一样solve(func1, x) % 传入参数func1,这是一个函数句柄,函数默认求其零点ans= % 命令行输出,三个解,为3*1的符号向量。对以上五种输入输出都完全一样-5520 |
对于不可符号求解的函数零点/方程解,solve抛出警告并返回一个数值解:
1 2 3 4 5 6 | exp1 = atan(x) - x - 1; % 不可符号求零点的表达式solve(exp1 == 0, x) % 命令行输入% 命令行输出:警告: Cannot solve symbolically. Returning a numeric approximation instead.ans =-2.132267725272885131625420696936 |
值得注意的是,虽然称之为“数值解”,并且输出了一个位数非常多的小数,但查看数据类型发现ans的数据类型依然是符号变量。其实,如果是正常的double类型的变量,直接输出是不可能给出这么多位的。matlab里面默认打印精度是4位小数,可以用 format long 语句调整到15位小数,和机器精度基本持平。
solve也可以求解方程组,此时输入的表达式epn和变量var为行向量(亲测列向量不可用):
1 2 3 4 5 6 7 8 9 10 11 12 | exp1 = [x^2/9 + y^2/4 == 1, 2*x - 3*y == 0]; % 联立椭圆方程和直线方程solution = solve(exp1, [x, y]); % 解方程组% 命令行输出solution = 包含以下字段的
% 这意味着x和y均有两个解。函数输出的solution是一个struct,访问方法和C语言访问struct成员一样:struct.x % 命令行输入ans= % 命令行输出 (3*2^(1/2))/2-(3*2^(1/2))/2 |
可以看出,当solve给出符号解的时候,它是不会化简计算的。任何matlab的符号计算,包括四则运算、求导积分,都不具备化简/数值计算的功能。
此外,solve函数还有一些选项可选,这使得符号求解名副其实,这才是solve的强大之处。运用solve函数,Name设定为'ReturnConditions',其值设定为true,表示要求solve函数输出详细信息。用这个方法我们可以得出一族解:
1 2 3 4 5 6 7 | % 求解方程sin(x)=cos(x),我们知道这个方程有无穷多解[solution, parameter, condition] = solve(sin(x)==cos(x), x, 'ReturnConditions', true);% 命令行输出solution = pi/4 + pi*k
% parameter输出的是构成解的参数(符号变量)condition =in(k, 'integer'); % condition表明parameter的条件,此处k为整数 |
而一般地,对于多变量的多项式(组),当多项式数量不足以确定所有参数时,按照以上设定,solve函数可以解出几个变量关于其他变量的函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
solution.x % 命令行输入:访问solution结构体的x参数
(3*2^(1/2)*(-(z - 1)*(z + 1))^(1/2))/2-(3*2^(1/2)*(-(z - 1)*(z + 1))^(1/2))/2% 结构体还有参数parameters和conditions。此处没有新生成的参数,因此parameters和conditions没有意义solution.parameters % 命令行输入ans =Empty sym: 1-by-0solution.conditions % 命令行输入
TRUETRUE |
在solve中,还可以使用 assume 函数来规定符号变量的性质(如整数、大于零、区间等等)。
2. 多初值的数值解方程(组)函数 vpasolve
官方参考页:Solve equations numerically - MATLAB vpasolve
vpasolve是一款数值解方程(组)的函数。输入一些个参数,返回符号型数值标量/向量(即以数值的形式显示但实际上还是符号变量)。它的基本使用方式是:
1 |
|
它的输入、功能和输出都和solve相仿。方程组的输入同样为行向量,变量组的输入也一样。
当输入一个可以定解的多项式方程(组)时,vpasolve将会直接给出方程的数值解;若多项式方程数量不足以确定所有的解,那么vpasolve将会给出以剩余变量表示的所求变量的函数,只是表达式的一部分(系数等)可能会以数值的形式呈现。注意,有理分式方程将会多项式化以后一样处理。对于这些方程,init_guess的值写了也没用。
1 2 3 4 5 | exp1 = (x-1)*(x-2)/(x-3); % 分式方程solution = vpasolve(exp1, x) % 命令行输入solution = % 命令行输出,得到了全部解1.02.0 |
>> exp1 = [x^2/9 + y^2/4 == 1, 2*x - 3*y == 0]; % 联立椭圆方程和直线方程
solution = vpasolve(exp1, [x, y]); % 解方程组
>> solution
solution =
包含以下字段的 struct:
x: [2×1 sym]
y: [2×1 sym]
>> solution.x
ans =
-2.1213203435596425732025330863145
2.1213203435596425732025330863145
>> solution.y
ans =
-1.4142135623730950488016887242097
1.4142135623730950488016887242097
对于多元方程组,vpasolve的输出也是struct结构体,访问方法也和solve输出的struct一样。不同的是,vpasolve无法求出含参的解,即无法设定'ReturnConditions'选项。和solve类似,除了多项式方程和有理分式方程以外的任何方程,vpasolve都不会给出全部解。这样一看,似乎vpasolve只不过就是把solve的结果全部转化为数值形式,甚至许多solve的功能都不能满足。这样的想法当然不对,vpasolve也有其自身的优势,这来源于:
A)可以设置初值进行数值求解。对于不可符号求解的方程,solve因为没有设定初值,可能无法搜索到合适的解。vpasolve则可以设置初值,从而可以进行后续解的搜索;B)可以随机取初值。我们都知道求解方程和最优化问题的初值选取非常玄学,而同样的初值最多只能有一个解。而结合循环等控制语句,利用vpasolve的随机初值功能可以让这一过程变得比较简单。比如可以写作初等函数的半整数阶Bessel(贝塞尔)函数,其零点有无穷多,但无法通过符号方法求解,在solve中会遇到很大的问题,但是用vpasolve设置合适的初值可以得到许多组临近初值的解。比如:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | syms x;exp1 = sin(x)/x;exp1 = diff(exp1, x); % 对原函数求导,得到的函数零点和3/2阶贝塞尔函数的零点相同% 命令行输入solution = solve(exp1, x)% 命令行输出,每次得到的结果均一样,为一个很遥远的解警告: Cannot solve symbolically. Returning a numeric approximation instead.solution =-227.76107684764829218924973598808solution = vpasolve(exp1, x, 1) % 命令行输入solution = % 命令行输出大概就是00.00000000000000000000000014187233415524662526214503949551solution = vpasolve(exp1, x, 3) % 命令行输入solution = % 命令行输出4.4934094579090641753078809272803 |
另外,一些有限个解的方程,比如 ,我们已经知道它有解0,根据画图还可以确定在x>0和x<0范围内各有一个解。根据atanx的性质,我们知道所有的解肯定在区间[-5,5]之中。如果使用solve,每次均有警告并且输出一样,无法获得三个不同的解;即使是之后讲的fsolve也需要每次给定初始估计(init guess)。对于vpasolve,当确定范围了以后可以简单地使用循环的控制语句,只需要规定随机撒点的区间为[-5,5]:
1 2 3 4 5 6 | syms x;exp1 = atan(x) - x/2;for i= 1:5 solution = vpasolve(exp1 == 0, x, [-5, 5], 'Random', true); disp(solution);
|
输出结果:
1 2 3 4 5 | -1.3628993400364241574879337535051e-53 % 也差不多即02.3311223704144226136678359559171 % 这就是要求的正根-2.3311223704144226136678359559171 % 这就是要求的负根,和正根关于原点对称2.33112237041442261366783595591710 |
很轻松地得到了该方程的全部解而不用再去手动猜测了。
3. 数值解方程(组)函数 fsolve
官方参考页:Solve system of nonlinear equations - MATLAB fsolve
fsolve可能是目前matlab的内置库函数中最常用的求(非线性)方程(组)解的函数,也是最为人熟知的。它用于数值求解方程(组),具有较广的适用范围(适用于高维和非线性、非多项式情形),甚至可以求矩阵方程的解(即甚至可以求解未知量为矩阵的情景)。fsolve函数的基本形式是:
1 2 3 | [x, fval, exitflag, output, jacobian] = fsolve(func, init_guess, options);% 输入函数句柄func,初值(向量)init_guess,求解选项options(可缺省);% 输出解x,x处值fval(也就是残差,可缺省),计算终止信息exitflag、输出信息output、x处雅可比矩阵jacobian(均可缺省) |

对于非线性方程组F(X)=0,用fsolve函数求其数值解。fsolve函数的调用格式为:
X=fsolve('fun',X0,option)
其中X为返回的解,fun是用于定义需求解的非线性方程组的函数文件名,X0是求根过程的初值,option为最优化工具箱的选项设定。最优化工具箱提供了20多个选项,用户可以使用optimset命令将它们显示出来。如果想改变其中某个选项,则可以调用optimset()函数来完成。例如,Display选项决定函数调用时中间结果的显示方式,其中‘off’为不显示,‘iter’表示每步都显示,‘final’只显示最终结果。optimset(‘Display’,‘off’)将设定Display选项为‘off’。
例1:求下列非线性方程组在(0.5,0.5) 附近的数值解。
(1) 建立函数文件myfun.m。
function q=myfun(p)
x=p(1);
y=p(2);
q(1)=x-0.6*sin(x)-0.3*cos(y);
q(2)=y-0.6*cos(x)+0.3*sin(y);
(2) 在给定的初值x0=0.5,y0=0.5下,调用fsolve函数求方程的根。
x=fsolve('myfun',[0.5,0.5],optimset('Display','off'))
x =
0.6354
0.3734
将求得的解代回原方程,可以检验结果是否正确,命令如下:
q=myfun(x)
q =
1.0e-009 *
0.2375 0.2957
可见得到了较高精度的结果。
备注:在MATLAB中使用fsolve相对应的function 函数定义时,变量与变量之间除了加减之外的运算如"*,/,^"等符号应该在前面加上“.”,类似于矩阵或者向量的点乘,否则最优运算不能进行,而且系统并不提示出错。
例1:
f=@(x) [2.*x(1)-x(2)-exp(-x(1));-x(1)+2.*x(2)-exp(-x(2))];
fsolve(f,[-5,-5])
运行代码得到:
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
<stopping criteria details>
ans =
0.5671 0.5671
例2:非线性方程组:
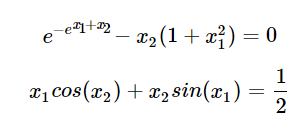
这是一个迷一般的方程组,嵌套的自然指数让人十分混乱,我们也并不期望得到这个方程的符号解或者解析解。我们将该方程组转化为matlab函数句柄:
1 2 3 4 5 | x = sym('x', [1,2]);% 生成符号变量向量f = [exp(-exp(-x(1)+x(2))) - x(2)*(1 + x(1)^2), x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5];% 生成函数句柄func,该句柄的输入参数为一向量func = matlabFunction(f, 'Vars',{[x(1), x(2)]}); |
然后调用fsolve对于函数func进行求解,输出一个求解消息和解solution:
1 2 3 4 5 6 7 8 9 | % 命令行输入solution = fsolve(func, [0,0])% 命令行输出Equation solved.fsolve completed because the vector of function values is near zeroas measured by the default value of the function tolerance, andthe problem appears regular as measured by the gradient.solution = 0.3931 0.3366 |

需要注意的是,fsolve输入的函数句柄func只接受一个变量!
>> f = @(x) [2.*x(1) - x(2) - exp(-x(1)); -x(1) + 2.*x(2) - exp(-x(2))];
fsolve(f,[-5,-5])
ans =
0.5671 0.5671
%如果是给出两个变量则出错
>> f = @(x,y) [2.*x - y - exp(-x); -x + 2.*y - exp(-y)];
fsolve(f,[-5,-5])
输入参数的数目不足。
出错 @(x,y)[2.*x-y-exp(-x);-x+2.*y-exp(-y)]
出错 fsolve (第 258 行)
fuser = feval(funfcn{3},x,varargin{:});
原因:
Failure in initial objective function evaluation. FSOLVE cannot continue.
%初始目标函数评估失败。FSOLVE无法继续。
fsolve可用于高维的情形,如例子中的二维,是通过将函数句柄的输入转化为向量实现的,即func接受一个向量形式的变量。对于创建一个输入参数为向量的函数句柄,简单地采用@方法似乎是行不通的。以上采用的方法是利用函数matlabFunction,定义变量('Var')为向量[x(1),x(2)],从而将符号变量f转化为函数句柄func。另一种可能更加普适(但更加麻烦)的方法参见官方参考页的示例或者matlab中函数fsolve的help文档,通过定义一个函数文件来实现这一操作(函数function文件和函数句柄是等价的)。
函数fsolve提供了一些可以作为输出设置的options选项。options的设置如下:
1 2 3 | options = optimoptions('fsolve', 'Display', opt1, 'PlotFcn', opt2);% opt1可以填 'none'/'off'(无额外显示)/'iter'(迭代信息表格)% opt2可以填函数 @optimplotfirstorderopt 绘制一阶极值条件随迭代的变化 |
现在,尝试使用'iter'和'@optimplotfirstorderopt选项:
1 2 3 4 5 6 7 8 9 10 | options = optimoptions('fsolve', 'Display', 'iter', 'PlotFcn', @optimplotfirstorderopt);solution = fsolve(func, [0,0], options);% 除了上述输出,还有了另外的输出: Norm of First-order Trust-region Iteration Func-count f(x) step optimality radius 0 3 0.385335 0.503 1 1 6 0.0336737 0.642449 0.206 1 2 9 0.000110235 0.122659 0.0162 1.61 3 12 8.13142e-11 0.00681475 1.13e-05 1.61 4 15 4.11698e-22 7.0962e-06 3.06e-11 1.61 |
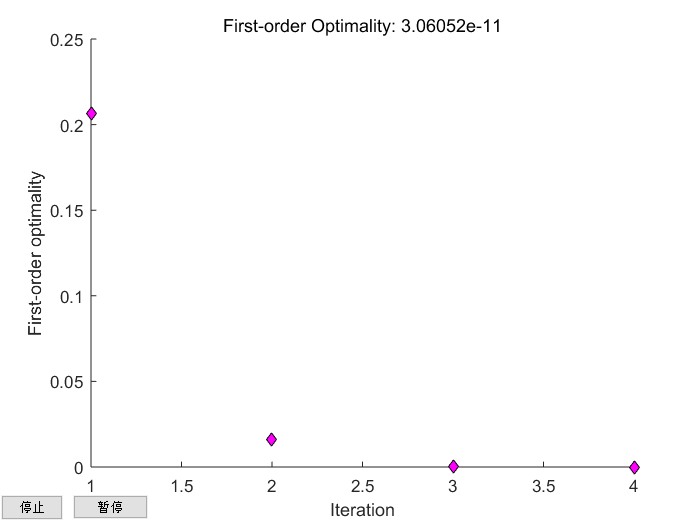
输出内容中,iteration为迭代次数,func-count为函数的总调用次数,f(x)为函数值的一个性质(暂时还没搞清楚是啥,毕竟二维映射不可能只有一个值),Norm of step应当是迭代步长(相邻迭代点间隔)的范数(模长),first order optimality 一阶优化条件,最终迭代是否终止的判据就是一阶优化条件是否足够接近零。绘图可以看出,随着迭代的进行,一阶优化条件趋于零。
理论上,fsolve函数还允许指定求解的算法,比如使用单纯信赖域,或者使用狗腿信赖域,或者使用Levenberg-Marquardt算法。但总而言之,fsolve的算法均属优化算法,也因此在这里不足以讨论完全,留待优化部分的笔记说明。
数值寻根方法
方法1:平分法bisection method
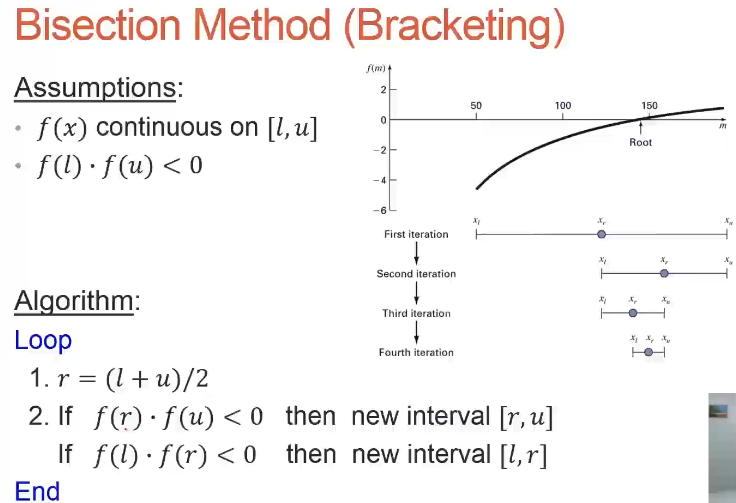
1、Assumptions:(假设)
continuous on [l,u](函数在区间内连续)
(函数有穿过x轴,即被x轴分割)
2、Algorithm(算法)
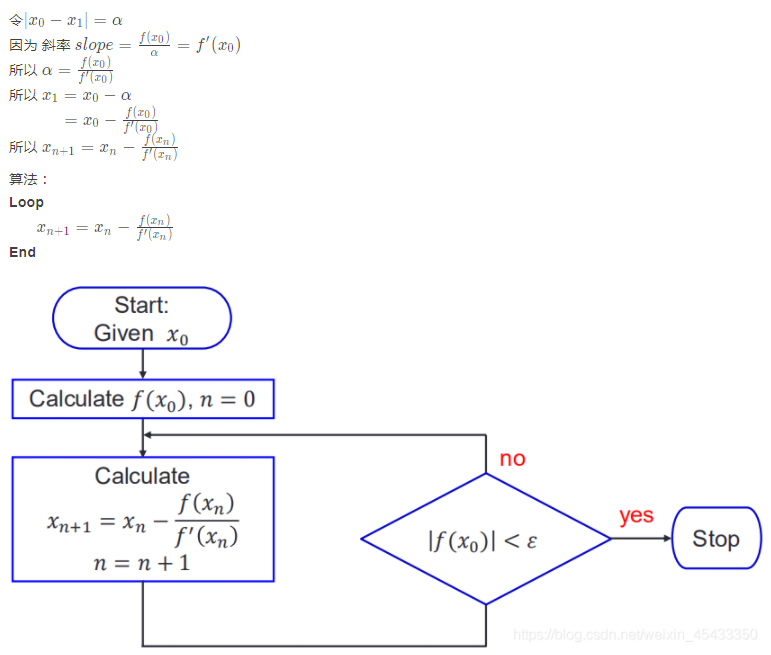
Bisection Algorithm Flowchart(等分算法流程图)
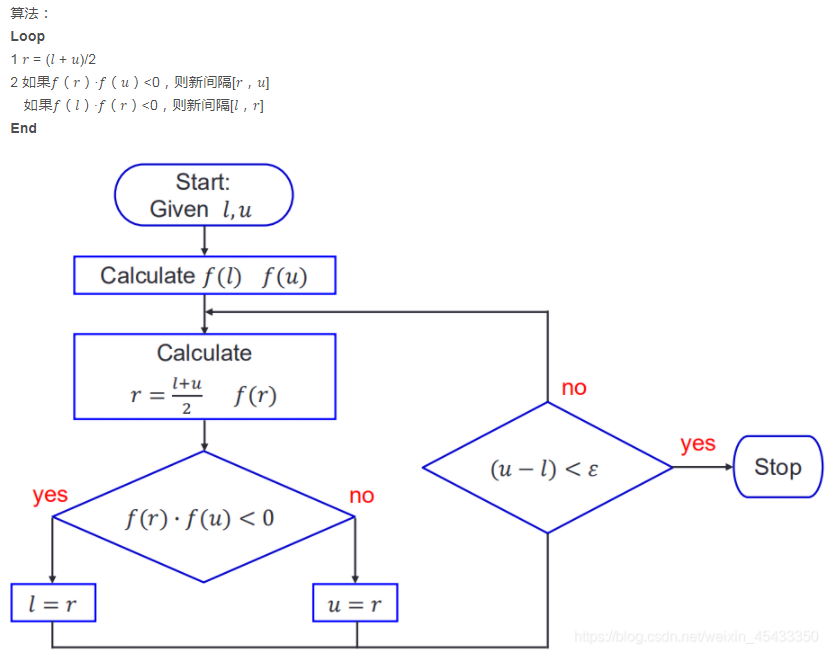
例:以函数f(x)=log_2 x的近似解为例【手算:f(x)=0时,x=1】
clear;
l = 0.000000001; %0不在log函数定义域内,取0+即可
u = 5; %取很大的整数值也可以
f1 = log2(l); %计算()
f2 = log2(u); %计算()
while (u-l) >= 0.000001 %进入循环(while的判断条件为:如果条件为真,则完成循环内操作)
r = (l + u)/2; %取中点r
f3 = log2(r); %计算中点的函数值
if f3*f2 < 0 %进入判断
l = r;
f1 = f3;
else
u = r;
f2 = f3;
end
end
disp(r) %显示找到的根
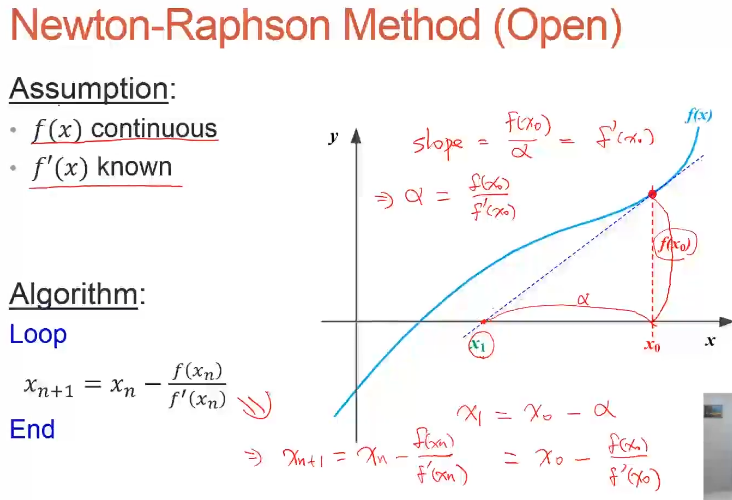
方法2:开放式方法(如牛顿-拉夫逊法Newton-Raphson method)
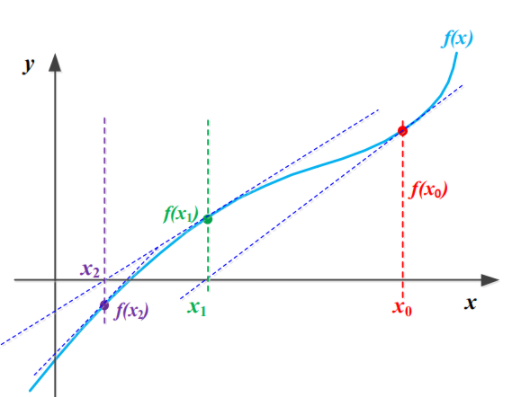
从一个或多个初始猜测点开始
是一个开放区间,没有一个具体的区间给我们。
初始假设:
函数连续;
一阶微分可求。
使用方法:
给一个初试的x0值,
计算该点的函数值,
计算该点的斜率,
找到该点的切线和x轴相交的点x1,
再以x1点继续执行上面的步骤,
重复执行直到找到解。
例:
clear;
n = 0;
x0 = 0.00000000001; %给出一个初始值
f0 = log2(x0); %求初始值的函数值
syms x; %给定一个符号变量
f = log2(x); %给定符号变量下的函数表达式
f_wf = diff(f); %求函数变量形式下的一阶微分方程表达式
while abs(f0) >= 0.00000000001 %进入循环:如果条件为真(在这里规定的一个精度值,如果是0算不出来),那继续执行
f_wf_f0 = subs(f_wf,x,x0); %求f0的微分值
x1 = x0 - f0/f_wf_f0; %算x1的值
n = n+1;
x2 = double(x1); %取双精度浮点数值类型
disp(x2); %显示每次求解,切线和x轴的交点并显示,体现计算过程
x0 = x2; %把转换数值形式后的值赋给x0,进行下一回合计算
f0 = log2(x0); %求新的斜率
end
output = sprintf('The root is: %8.5f',x0);
disp(output) %显示求得的解
===命令行窗口===
>> class11_practice1_P22
2.6328e-10
6.0708e-09
1.2093e-07
2.0471e-06
2.8862e-05
3.3056e-04
0.0030
0.0203
0.0995
0.3290
0.6947
0.9478
0.9986
1.0000
1.0000
The root is: 1.00000
4. 数值求一维函数零点函数 fzero
x = fzero(fun,x0):从x0开始,尝试求出离x0最近的 fun(x) = 0 的解,此解是 fun(x) 变号的位置,即f(x-),f(x+)异号。fzero 无法求例如 x^2 这类函数的根。
若x0是一个向量[a,b],则[a,b]即为寻根的范围:(注意与fslove()不同)

更多官方参考页:非线性函数的根 - MATLAB fzero
fzero用于求函数零点。这个函数致力于求解一维函数的零点。其基本形式:
1 | x = fzero(func, init_guess, options) % func为函数句柄,init_guess为初值,options可以包括其他要求(可缺省) |
fzero在应用上最令人高兴的是其丰富的输出内容,有利于观察迭代的结果,这用到options控制。options的控制方法为:
1 | options = optimset(A, B); % A为一个选项名,B为该选项值 |
然后将options变量带入函数即可。具体可以参见参考页,在此举两个例子,比如希望输出迭代的每一步:
1 2 3 4 | options = optimset('Display', 'iter'); % 设定'Display'选项为'iter'模式func = @(x)x^3 + x + 5;zeropt = fzero(func, 10, options);disp(zeropt); |
则有输出(节选):
1 2 3 4 5 6 7 8 9 10 11 12 13 | Func-count x f(x) Procedure 26 -4.05097 -65.5287 initial 27 -3.40338 -37.8248 interpolation 28 -2.541 -13.9473 interpolation 29 -2.541 -13.9473 bisection 30 -1.65947 -1.22938 interpolation 31 -1.57533 -0.484774 interpolation 32 -1.52086 -0.0386585 interpolation 33 -1.51616 -0.00138072 interpolation 34 -1.51598 -4.15907e-06 interpolation 35 -1.51598 -4.49535e-10 interpolation 36 -1.51598 -8.88178e-16 interpolation 37 -1.51598 -8.88178e-16 interpolation |
从中,我们可以看到每一步的x变化,f(x)的取值,甚至每一次迭代执行的操作:是二分法(bisection)或者插值类方法(interpolation)。我们还可以将迭代步骤可视化:
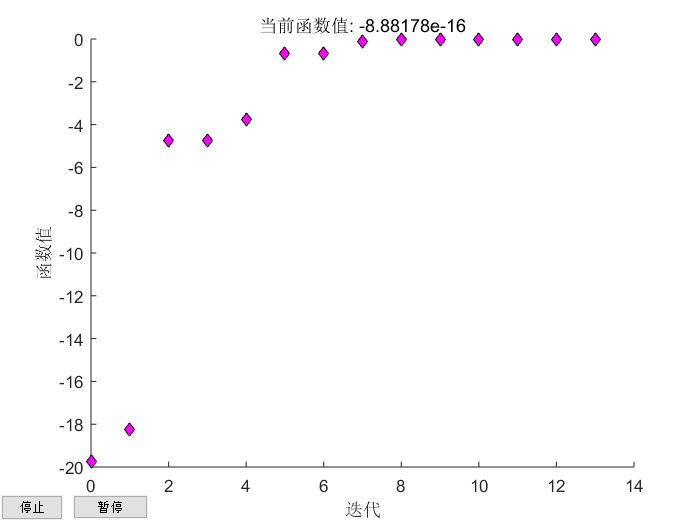
1 2 3 4 | options = optimset('PlotFcns', @optimplotfval); % 每次输出函数值func = @(x)x^3 + x + 5;zeropt = fzero(func, 0, options);disp(zeropt); |
输出图片:
在MATLAB中提供了一个fzero函数,可以用来求单变量非线性方程的根。该函数的调用格式为:z=fzero('fname',x0,tol,trace)
其中fname是待求根的函数文件名,x0为搜索的起点。一个函数可能有多个根,但fzero函数只给出离x0最近的那个根。tol控制结果的相对精度,缺省时取tol=eps,trace指定迭代信息是否在运算中显示,为1时显示,为0时不显示,缺省时取trace=0。

%画出函数图像,对该函数有个大概的印象
t=-10:0.01:10;
y=sin(t).^2.*exp(-0.1*t)-0.5*abs(t);
plot(t,y)
hold on
plot([-10 10],[0 0],'k');
%从图像我们可以看出大概在x=[-2-1 0 1 2]附近的某个值时,y为零。下面我们就用fzero来具体求出零点。
f=@(t)sin(t).^2.*exp(-0.1*t)-0.5*abs(t)
%第一种方法使用arrayfun
%x=[-2 -1 0 1 2];
%arrayfun(@(x)fzero(f,x),x)
%第二种方法,分别带入
[x1 y]=fzero(f,-2)
[x2,y]=fzero(f,-1)
[x3,y]=fzero(f,0)
[x4,y]=fzero(f,1)
[x5,y]=fzero(f,2)
arrayfun(@(x)fzero(f,x),x)
使用fzero和fsolve对单个变量方程有区别吗?
就在这里.我只想提到两者之间最直接的区别:
07000 can be used to solve for the zero of a single variable equation. However, 07001 will find the zero if and only if the function crosses the x-axis.
这是一个简单的例子:考虑函数f = x ^ 2.该函数对于x的所有实数值都是非负的.这在x = 0时有一个根.我们将匿名函数定义为f =@(x)x.^2;并尝试使用这两种方法找到根.
使用fsolve:
options=optimset('MaxIter',1e3,'TolFun',1e-10);
fsolve(f,0.1,options)
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the selected value of the function tolerance, and
the problem appears regular as measured by the gradient.
<stopping criteria details>
ans =
1.9532e-04
不是零,而是接近.
使用fzero:
fzero(f,0.1)
Exiting fzero: aborting search for an interval containing a sign change
because NaN or Inf function value encountered during search.
(Function value at -1.37296e+154 is Inf.)
Check function or try again with a different starting value.
ans =
NaN
它找不到零.
考虑函数f =@(x)x.^3的另一个例子;穿过x轴并且在x = 0时具有根.
fsolve(f,0.1)
ans =
0.0444
fzero(f,0.1)
ans =
-1.2612e-16
在这种情况下,fsolve也不会返回0.即使使用我在上面定义的选项,也只能通过fsolve获得0.0017.但是,fzero的答案在机器精度范围内是正确的!答案的差异不是因为算法效率低下.这是因为他们的目标不同.
fzero有一个明确的目标:找到零!简单.那里没有含糊之处.如果它穿过x轴,则为零,它将找到它(仅限实数).如果它不交叉,它会发出呜呜声.
但是,fsolve的范围更广.它旨在解决非线性方程组.通常,您无法找到这些方程的精确解,并且必须设置容差级别,在此范围内您愿意接受解决方案作为答案.因此,需要手动设置许多选项和公差来按摩确切的根.当然,你有更好的控制,但为了找到单个var方程的零,我认为这是一个痛苦.在这种情况下我可能会使用fzero(假设它穿过x轴).
除了这个主要差异之外,在实现和使用的算法方面存在差异.为此,我将向您介绍有关这些功能的在线文档(请参阅上面的链接).
单元非线性方程可用fzero,多元非线性方程可用fsolve.对比:
[x,fval,exitflag,output]=fzero(fun,x0)
[x,fval,exitflag,output]=fsolve(fun,x0)
【例1】单元非线性方程求解:计算sin(x)在3附近的零点(可以间接求π).
解:主函数
[x,fval,exitflag,output]=fzero('sin(x)',3)
解得:
x =
3.1416
【例2】单元非线性方程求解:求

方法1—解:fun013.m
f=@(x)x^3-2*x-5
主函数
[X1,fval,exitflag,output]=fzero(f,2)
解得:
X1 = 2.0946
方法2—解:主函数
C=[1 0 -2 -5];
X1=roots(C);
for i=1:3
if imag(X1(i))==0
disp(X1(i))
end
end
解得:X2= 2.0946
【例3】多元非线性方程(组)求解:

解:fun014.m
function f=fun014(x)
f=[2*(x(1))^2-x(2)+1; -(x(1))^2+2*x(2)-5]
主函数
clear
clc
x0=[0,0];
[x,fval]=fsolve(@fun014,x0)
解得:
x =
1.0000 3.0000
5. 数值求多项式零点函数 roots
官方参考页:多项式根 - MATLAB roots
除了求多项式根啥也干不了的一个函数,输入也和其他求根函数迥异。roots的标准形式如下,输入一个行向量,返回一个double型的列向量:
1 | r = roots(p); % 其中,p为一个行向量,里面依次为多项式降次排序时各次项系数(若无该次则写0) |
roots也不是一无是处。相比于fzero和fsolve这样的函数,roots可以给出多项式的所有解,包括实数解和复数解:
1 2 3 4 5 | p = roots([1, 0, 0, -1]) % 命令行输入p = % 命令行输出三个解,其中一对共轭复根,一个实根 -0.5000 + 0.8660i -0.5000 - 0.8660i 1.0000 + 0.0000i |
6 常微分方程初值问题的数值解法
龙格-库塔法的实现
基于龙格-库塔法,MATLAB提供了求常微分方程数值解的函数,一般调用格式为:
[t,y]=ode23('fname',tspan,y0)
[t,y]=ode45('fname',tspan,y0)
其中fname是定义f(t,y)的函数文件名,该函数文件必须返回一个列向量。tspan形式为[t0,tf],表示求解区间。y0是初始状态列向量。t和y分别给出时间向量和相应的状态向量。
例 设有初值问题,试求其数值解,并与精确解相比较(精确解为y(t)=)。
(1) 建立函数文件funt.m。
function yp=funt(t,y)
yp=(y^2-t-2)/4/(t+1);
(2) 求解微分方程。
t0=0;tf=10;
y0=2;
[t,y]=ode23('funt',[t0,tf],y0); %求数值解
y1=sqrt(t+1)+1; %求精确解
t'
y'
y1'
y为数值解,y1为精确值,显然两者近似。
7. 函数极值
MATLAB提供了基于单纯形算法求解函数极值的函数fmin和fmins,它们分别用于单变量函数和多变量函数的最小值,其调用格式为:
x=fmin('fname',x1,x2)
x=fmins('fname',x0)
这两个函数的调用格式相似。其中fmin函数用于求单变量函数的最小值点。fname是被最小化的目标函数名,x1和x2限定自变量的取值范围。fmins函数用于求多变量函数的最小值点,x0是求解的初始值向量。
MATLAB没有专门提供求函数最大值的函数,但只要注意到-f(x)在区间(a,b)上的最小值就是f(x)在(a,b)的最大值,所以fmin(f,x1,x2)返回函数f(x)在区间(x1,x2)上的最大值。
例 求f(x)=x3-2x-5在[0,5]内的最小值点。
(1) 建立函数文件mymin.m。
function fx=mymin(x)
fx=x.^3-2*x-5;
(2) 调用fmin函数求最小值点。
x=fmin('mymin',0,5)
x=
0.8165
8.多项式计算
多项式求值:polyval(p,x)
多项式卷积:conv(a,b)
多项式求导:polyder(p,n)
多项式积分:polyint(p,k)
多项式求根:roots(p)
多项式拟合:polyfit(x,y,n)

可以用向量p = [1 0 -2 -5]表示.
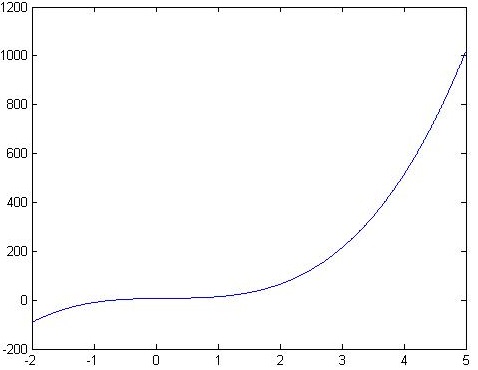
多项式求值:polyval()
使用polyval(p, x)可以计算多项式p在x的每个点处的值.
a = [9,-5,3,7];
x = -2:0.01:5;
f = polyval(a,x);
plot(x,f);
多项式的乘法:conv()使用conv(p1, p2)函数可以对两个向量p1和p2进行卷积相乘,用于计算多项式的乘法.
例如多项式: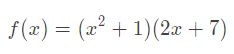
可以使用conv()函数得到展开后的多项式:p = conv([1 0 1], [2 7])得到p = [2 7 2 7].
and its derivative for
2、Hint:conv()
答案代码:
hold on;
a = [5 -7 5 10];
%x^3的系数要为5才能绘制老师的答案,别问我怎么知道的
b = [0 4 12 -3];
c = conv(a,b);%卷积和多项式乘法
x = -2:0.1:1;
f = polyval(c,x);%多项式计算值
%绘制f(x)函数
plot(x,f,'--b');
m=polyval(polyder(c),x);%polyder()求微分
%绘制f'(x)函数
plot(x,m,'-r');
xlim([-2,1])
ylim([-800,800])
legend('f(x)','f''(y)');
hold off;
box on多项式的数值运算
多项式的因式分解:roots()
使用roots(p)函数可以对多项式p进行因式分解,即求表达式值为0的根.
p = roots([1 -3.5 2.75 2.125 -3.875 1.25])
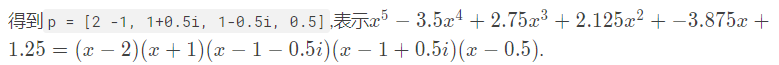
Polynomial Differentiation:polyder()(多项式微分)
1、Given
(1)What is the derivative of the function ?(函数的微分是什么)
(2)What is the derivative of the function value of ?
示例代码:
p = [5 0 -2 0 1]; q = polyder(p) polyval(q,7)%或者polyval(polyder(p),7)

Given
(1)What is the integral of the function with a constant of 3?
(2)What is the derivative of the function value of ?
示例代码:
p = [5 0 -2 0 1]; polyint (p,3)%当常数项为3时,求f(x)的积分 polyval(polyint (p,3),7)%求∫f(7)的值
9.数值微分
求差分:diff()使用diff(X, n)计算向量X的n阶差分,n默认为1.
x = [1 2 5 2 1]; diff(x); % 得到 [1 3 -3 -1] diff(x,1); % 得到 [1 3 -3 -1] diff(x,2); % 得到 [2 -6 2]
求导数:diff(y)./diff(x)
使用导数的定义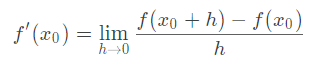
可以计算函数在某点的近似导数.
x0 = pi/2; h = 0.1; x = [x0 x0+h]; y = [sin(x0) sin(x0+h)]; m = diff(y)./diff(x) % 得到 m = -0.005
h的取值越小,得到的近似导数越精确.
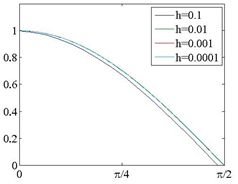
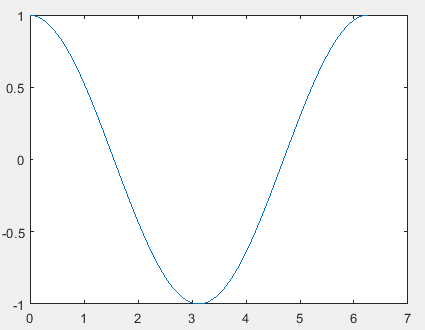
下面计算y=sin(x)的导数:
x=linspace(0,2*pi,200);
y=sin(x);
dy=diff(y)./diff(x); %数组dy的元素个数比数组x的长度少1
plot( x(1:end-1) , dy ) %dy的图像显示就是cos(x)的图像。
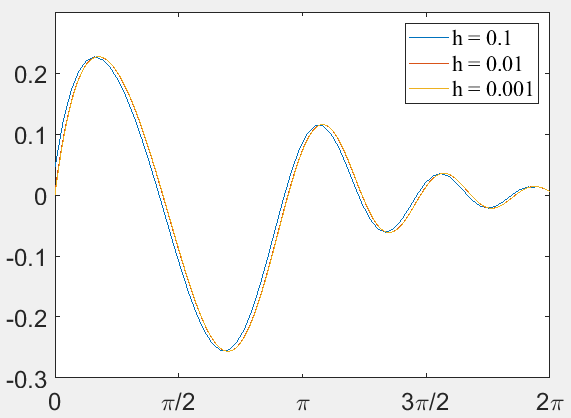
%尝试不同的步长,利用diff(y) ./ diff(x)计算出来的导数,光滑程度也不同。
g = colormap(lines);
hold on;
for i = 1:3
x = 0:power(10,-i):2 * pi; %分别采用不同步长
y = exp(-x) .* sin(power(x,2) ./ 2);
m = diff(y) ./ diff(x);
plot(x(1:end-1),m,'Color',g(i,:)); %采用不同的颜色输出
end
hold off
set(gca,'XLim',[0,2*pi]);
set(gca,'YLim',[-0.3,0.3]);
set(gca,'FontSize',18);
%set(gca,"FontName",'symbol');%R2018不用设置字体
set(gca,'XTick',0:pi/2:2*pi);
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'});
h = legend('h = 0.1','h = 0.01','h = 0.001');
set(h,'FontName','Times New Roman');
box on
下面程序计算f=x^3的一阶和二阶导数的值.
x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x); % 计算一阶导数
m2 = diff(m)./diff(x(1:end-1)); % 计算二阶导数
plot(x,y,x(1:end-1),m,x(1:end-2),m2);
xlabel('x'); ylabel('y');
legend('f(x) =x^3','f''(x)','f''''(x)', 4);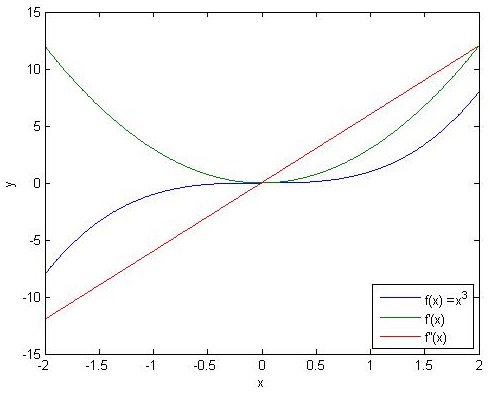
练习:
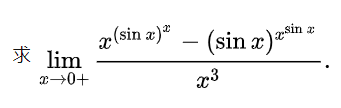
10.数值积分
数值积分原理
有三种常见算法用于计算数值积分: 矩形法,梯形法,抛物线法,它们分别把微分区间的图形视为矩形,梯形,抛物线以计算面积.
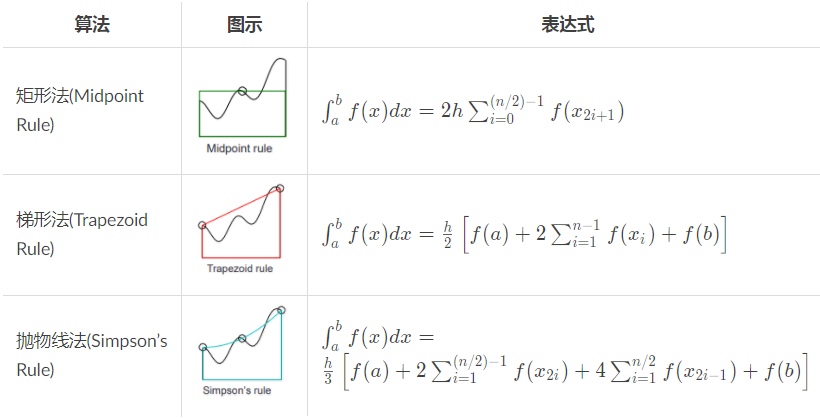
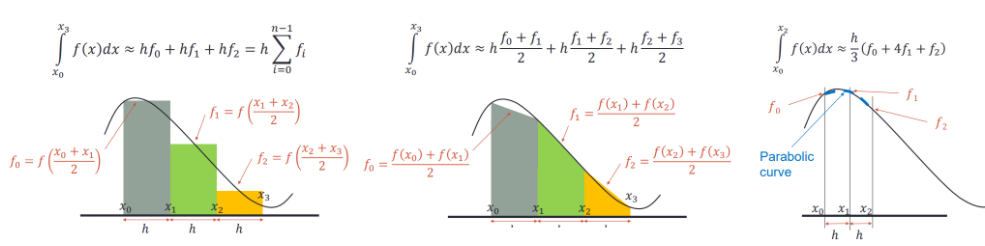
下面分别使用三种方法计算f=4x^3在区间0-2内的积分.
% 使用矩形法计算近似积分
clear all;
clc;
h=0.05;
x=0:h:2;
midpoint=(x(1:end-1)+x(2:end))./2; %求积分也就是求面积,算出每个中间点
y=4*midpoint.^3; % 用中间点带入到积分中,得出y值;
s=sum(h*y) %求出用宽度 h和高度 y的乘积并相加
%如果要精度更高,可以把 h 取小
或者:
h = 0.05; %缩小步距可以让偏差值更小
x = 0:h:2;
midpoint =(x+h/2);
y = 4 * midpoint(1:end-1) .^ 3;
s = sum(h * y);
s
% 使用梯形法计算近似积分
clear all; clc;
h = 0.05;
x = 0:h:2;
y=4*x.^3;
trapezoid = (y(1:end-1)+y(2:end))/2;
s = h*sum(trapezoid) % 得到 15.2246
clear all; clc; %trapz()来计算梯形数值积分
h=0.05;
x=0:h:2;
y=4*x.^3;
s=h*trapz(y) %trapz()来计算梯形数值积分
% 使用抛物线法计算数值积分,辛普森公式
s = h/3*(y(1)+2*sum(y(3:2:end-2))+4*sum(y(2:2:end))+y(end)) % 得到 15.8240
数值积分函数:integral()
integral(),integral2(),integral3()分别对函数在xmin至xmax间进行一重,二重,三重积分.
它们的第一个参数都应该是一个函数句柄,下面例子演示他们的用法:

clear all;
clc;
y=@(x) 1./(x.^3-2*x-5); %%有一个输入数
integral(y,0,2)
f=@(x,y) y.*sin(x)+x.*cos(y); %%有两个输入数
integral2(f,pi,2*pi,0,pi)
f=@(x,y,z) y.*sin(x)+z.*cos(y); %%有三个输入数
integral3(f,0,pi,0,1,-1,1)
integral
数值积分
语法
q = integral(fun,xmin,xmax)
q = integral(fun,xmin,xmax,Name,Value)
说明
q = integral(fun,xmin,xmax) 使用全局自适应积分和默认误差容限在xmin至 xmax间以数值形式为函数 fun 求积分。
q = integral(fun,xmin,xmax,Name,Value) 指定具有一个或多个 Name,Value对组参数的其他选项。例如,指定 'WayPoints',后跟实数或复数向量,为要使用的积分器指示特定点。
广义积分
创建函数  。计算 x=0至 x=Inf的积分。
。计算 x=0至 x=Inf的积分。
fun = @(x) exp(-x.^2).*log(x).^2;q = integral(fun,0,Inf)q = 1.9475
参数化函数
创建带有一个参数  的函数
的函数  。计算在 c=5时,计算从 x=0 至 x=2 的积分。
。计算在 c=5时,计算从 x=0 至 x=2 的积分。
fun = @(x,c) 1./(x.^3-2*x-c);q = integral(@(x)fun(x,5),0,2)q = -0.4605
练习:用多种方法求解积分

方法1:
y=@(x) (x.^2-x+1)./(x+3); z1=integral(y,0,10)
运行代码得到:
z1 =
29.0624
方法2:符号运算
syms x
y=(x^2-x+1)/(x+3);
answer=int(y,x,0,10) %直接求定积分
vpa(answer)
运行代码得到:
answer =
log(302875106592253/1594323) + 10
ans =
29.062381894314551580557148660356
方法3:符号运算
syms x
y=(x^2-x+1)/(x+3) ;
z=int(y,x) %先算出不定积分
answer=subs(z,x,10)-subs(z,x,0)
vpa(answer)
运行代码得到:
z =
13*log(x + 3) - 4*x + x^2/2
answer =
13*log(13) - 13*log(3) + 10
ans =
29.062381894314551580557148660356
方法4:数值计算
h=0.01;
x=0:h:10;
X_mid=(x(1:end-1)+x(2:end))/2; %求积分也就是求面积,算出每个中间点
y=(X_mid.^2-X_mid+1)./(X_mid+3); % 用中间点带入到积分中,得出y值;
s=sum(h*y) %求出用宽度 h和高度 y的乘积并相加
运行代码得到:
s =
29.0624