统计、拟合、插值
1.统计
描述性统计(Descriptive Statistics)
描述性统计主要研究数据的中心趋势(Central Tendency)和变异(Variation).

中心趋势(Central Tendency)
| 函数 | 作用 |
|---|---|
mean() | 计算平均值 |
median() | 计算中位数 |
mode() | 计算众数 |
prctile() | 计算百分位数 |
max() | 计算最大值 |
min() | 计算最小值 |

X = [1 3 5 5 5 5 7 9 9 9 10 13 14]; prctile(X, 0); % 数据的0%分位数为 0 prctile(X, 50); % 数据的50%分位数为 7 prctile(X, 100); % 数据的100%分位数为 14 prctile(X, 12.6); % 数据的12.6%分位数为 3.2760
综合实例2:中位数与均值的区别
>> x=[1.1,1.2,1.3,1.4,1.5,3,12,50,99]
x =
1.1000 1.2000 1.3000 1.4000 1.5000 3.0000 12.0000 50.0000 99.0000
>> y1=median(x) %中位数
y1 =
1.5000
>> y2=mean(x) %均值
y2 =
18.9444
%矩阵时=====================
a=randi(100,9,5)'
md1=median(a)
md2=median(a,2)
md_all=median(a,'all')
me1=mean(a)
me2=mean(a,2)
me_all=mean(a,'all')
运行上面代码:
a =
8 24 13 19 24 42 5 91 95
50 49 34 91 37 12 79 39 25
41 10 14 95 96 58 6 24 36
83 2 5 17 65 74 65 46 55
30 75 19 69 19 37 63 79 9
md1 =
41 24 14 69 37 42 63 46 36
md2 =
24
39
36
55
37
md_all =
37
me1 =
42.4000 32.0000 17.0000 58.2000 48.2000 44.6000 43.6000 55.8000 44.0000
me2 =
35.6667
46.2222
42.2222
45.7778
44.4444
me_all =
42.8667
下列函数绘制统计图表:
| 函数 | 作用 |
|---|---|
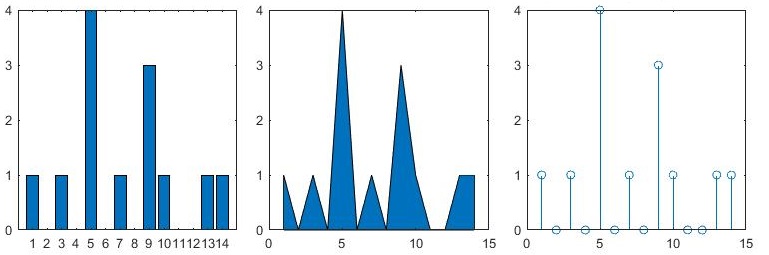
bar() | 绘制条形图 |
stem() | 绘制针状图 |
area() | 绘制填充图 |
boxplot() | 绘制箱线图 |
x = 1:14; freqy = [1 0 1 0 4 0 1 0 3 1 0 0 1 1]; subplot(1,3,1); bar(x,freqy); xlim([0 15]); subplot(1,3,2); area(x,freqy); xlim([0 15]); subplot(1,3,3); stem(x,freqy); xlim([0 15]);
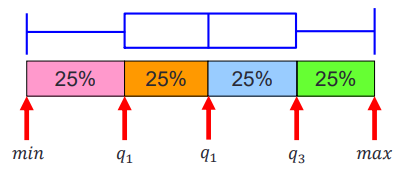
箱线图可以突出显示数据的四分位点.
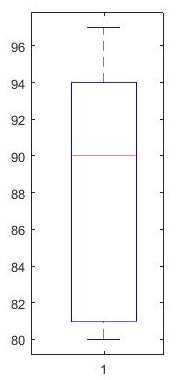
marks = [80 81 81 84 88 92 92 94 96 97]; boxplot(marks) prctile(marks, [25 50 75]) % 得到 [81 90 94]
变异(Variation)
离散程度
| 函数 | 作用 |
|---|---|
std() | 计算数据的标准差 |
var() | 计算数据的方差 |

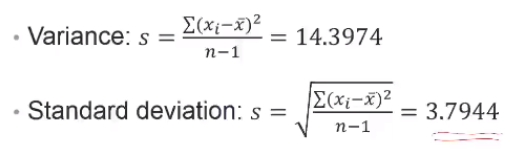
X = [1 3 5 5 5 5 7 9 9 9 10 13 14]; std(X); % 得到 3.7944 var(X); % 得到 14.3974
偏度(Skewness)
| 函数 | 作用 |
|---|---|
skewness() | 计算数据的偏度 |
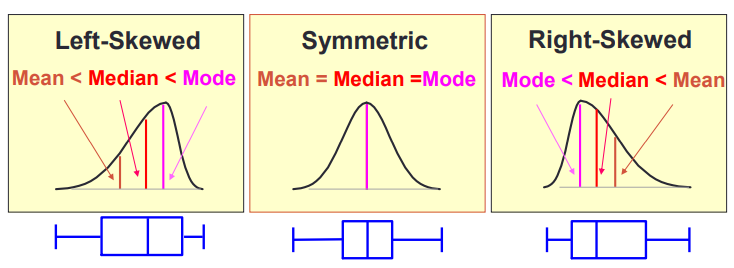
偏度反映数据的对称程度
数据左偏时,其偏度小于0.
数据完全对称时,其偏度等于0.
数据右偏时,其偏度大于0.
X = randn([10 3]); % 构造10*3的矩阵
X(X(:,1)<0, 1) = 0; % 将第一列数据右偏
X(X(:,3)>0, 3) = 0; % 将第二列数据左偏
boxplot(X, {'Right-skewed', 'Symmetric', 'Left-skewed'});
skewness(X); % 得到 [0.5162 -0.7539 -1.1234]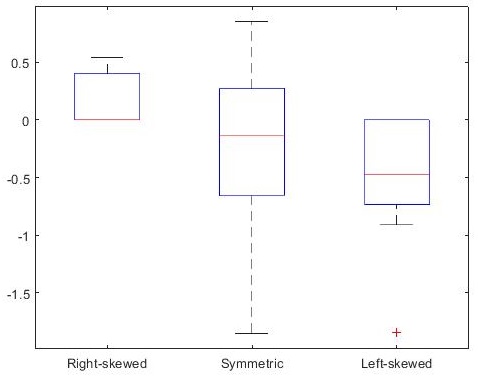
峰度(Kurtosis)
| 函数 | 作用 |
|---|---|
kurtosis() | 计算数据的峰度 |
峰度(Kurtosis)表征概率密度分布曲线在平均值处峰值的高低.直观来看,峰度反映了峰部的尖度.

统计推断(Inferential Statistics)
推论统计的核心即为假设检验.下列函数用于进行假设检验.
| 函数 | 作用 |
|---|---|
ttest() | 进行T检验 |
ztest() | 进行Z检验 |
ranksum() | 进行秩和检验 |
signrank() | 进行符号秩检验 |
load examgrades x = grades(:,1); y = grades(:,2); [h,p] = ttest(x,y);
执行上述程序,得到[h p] = [0 0.9805],表示在默认显著性水平(5%)下我们没有理由拒绝x与y同分布.
2.拟合


2.1 线性回归基础:最小二乘法
(一)Simple Linear Regression(简单线性回归)
1、A bunch of data points( )are collected(收集一些二维数据点)
如体重(Height)和身高(Weith)
2、Assume and
are linearly correlated(假设x和y线性相关)
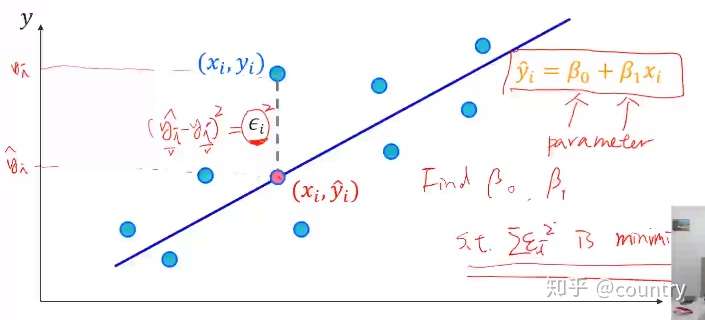
(二)Linear Regression Formulation(线性回归公式)
1、Define sum of squared errors(SSE):(定义平方误差之和)
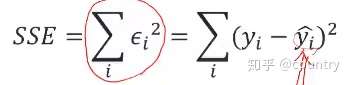
2、Given that the regression model:(假设回归模型)


(三)Solving Least-squares Problem(最小二乘问题的求解)
1、SSE is minimized when its gradient with respect to each parameter is equal to zero:(当SSE相对于每个参数的梯度等于零时,SSE最小)
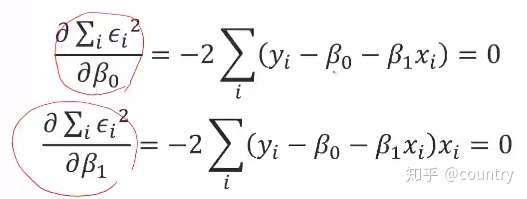
(四)Least-squares Solution(最小二乘解)
1、Suppose there exists N data points:(假设存在N个数据点:)
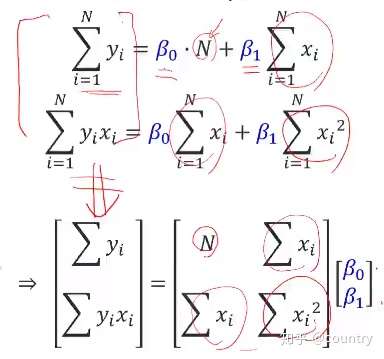
通过求解上述方程,可以得到B0,B1
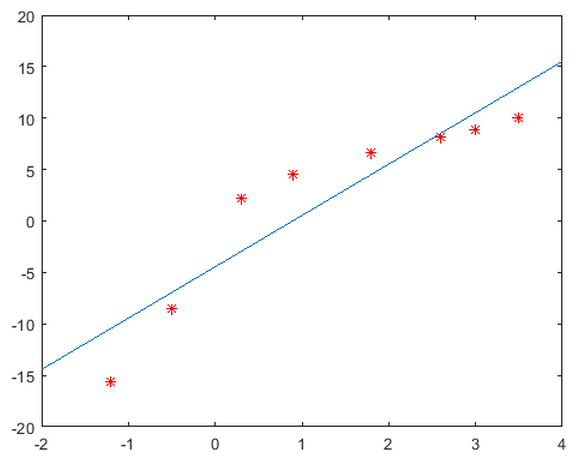
例:
clear
x = [-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y = [-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
N=length(x);
L=[sum(y) ; sum(x.*y)] ;
R=[N , sum(x) ; sum(x) , sum(x.^2)] ;
b=inv(R)*L;
b0=b(1)
b1=b(2)
x2=-2:0.1:4;
y2=b1*x2+b0;
plot(x,y,'*r',x2,y2)
2.2 matlab内置的多项式拟合函数polyfit()
p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数,该阶数是 y 中数据的最佳拟合(在最小二乘方式中)。p 中的系数按降幂排列,p 的长度为 n+1。
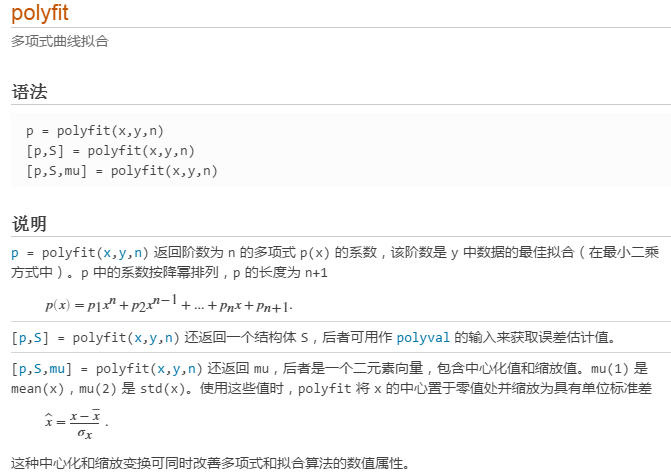
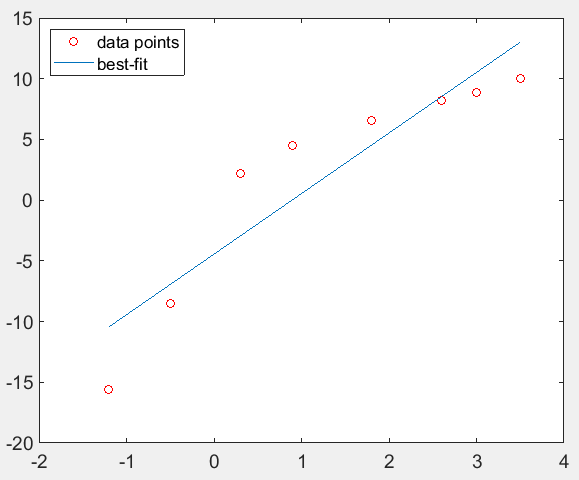
例:一次拟合练习
%一次拟合,设y=b1*x+b0
x = [-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y = [-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
fit = polyfit(x,y,1);%order,1次方的多项式
%poly会产生两个值fit(1)和fit(2)对应斜率和截距
%% 绘制图形
xfit = x(1):0.1:x(end);
%即xfit = [-1.2 -1.1 -1.0 ... 3.5]
yfit = fit(1) * xfit + fit(2);
%即y = ax + b
plot(x,y,'ro',xfit,yfit);
set(gca,'FontSize',14);
legend('data points','best-fit','Location','northwest');
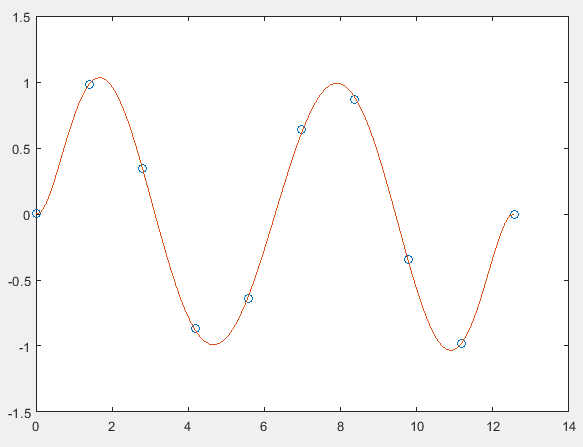
例:将多项式与三角函数拟合
%在区间 [0,4*pi] 中沿正弦曲线生成 10 个等间距的点。
x = linspace(0,4*pi,10);
y = sin(x);
%使用 polyfit 将一个 7 次多项式与这些点拟合。
p = polyfit(x,y,7);
%在更精细的网格上计算多项式并绘制结果图。
x1 = linspace(0,4*pi);
y1 = polyval(p,x1);
figure
plot(x,y,'o')
hold on
plot(x1,y1)
hold off
p =
-0.0001 0.0028 -0.0464 0.3702 -1.3808 1.9084 -0.1141 0.0002
使用polyfit(x, y, n)函数对数据x和y进行n次多项式拟合.
x = [-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y = [-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
figure('Position',[50 50 1500 400]);%可绘制区域的位置和大小
for i = 1:3
subplot(1,3,i);
p = polyfit(x,y,i);%多项式曲线拟合
%i = 1:3 分别画出了1次拟合,2次拟合,3次拟合
%拟合阶数越高,平均差值越小
xfit = x(1):0.1:x(end);
yfit = polyval(p,xfit);%多项式计算
plot(x,y,'ro',xfit,yfit);
set(gca,'FontSize',14);
ylim([-17,11]);
legend('Data points','Fitted curve','Location','southeast');
end


2)相关系数函数:corrcoef( )
corrcoef( ),用来衡量两个变量自己的相关度。


x=randn(1,1000);
y=randn(1,1000);
corrcoef(x,y ) %因为x,y都是随机序列,所以彼此之间的相关度几乎为0。
ans =
1.0000 -0.0280
-0.0280 1.0000
3)多元线性拟合:regress()使用regress(y, X)函数对数据X和y进行多元线性回归.
load carsmall;
y = MPG; x1 = Weight; x2 = Horsepower; % 导入数据集
X = [ones(length(x1),1) x1 x2]; % 构建增广X矩阵
b = regress(y,X); %是求系数,y=b(1)+b(2)*x1+b(3)*x2;在求的过程会把NaN的值去掉,也就是无效值
% 下面是绘图语句
x1fit = min(x1):100:max(x1); %求x1fit的点。按从小到大就可以知道range是多少,然后每隔100取一个点
x2fit = min(x2):10:max(x2); %求x2fit的点。每隔10个取一个点
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);
YFIT = b(1)+b(2)*X1FIT+b(3)*X2FIT;
scatter3(x1,x2,y,'filled');
hold on;
mesh(X1FIT,X2FIT,YFIT);
hold off;
xlabel('Weight');
ylabel('Horsepower');
zlabel('MPG');
view(50,10);

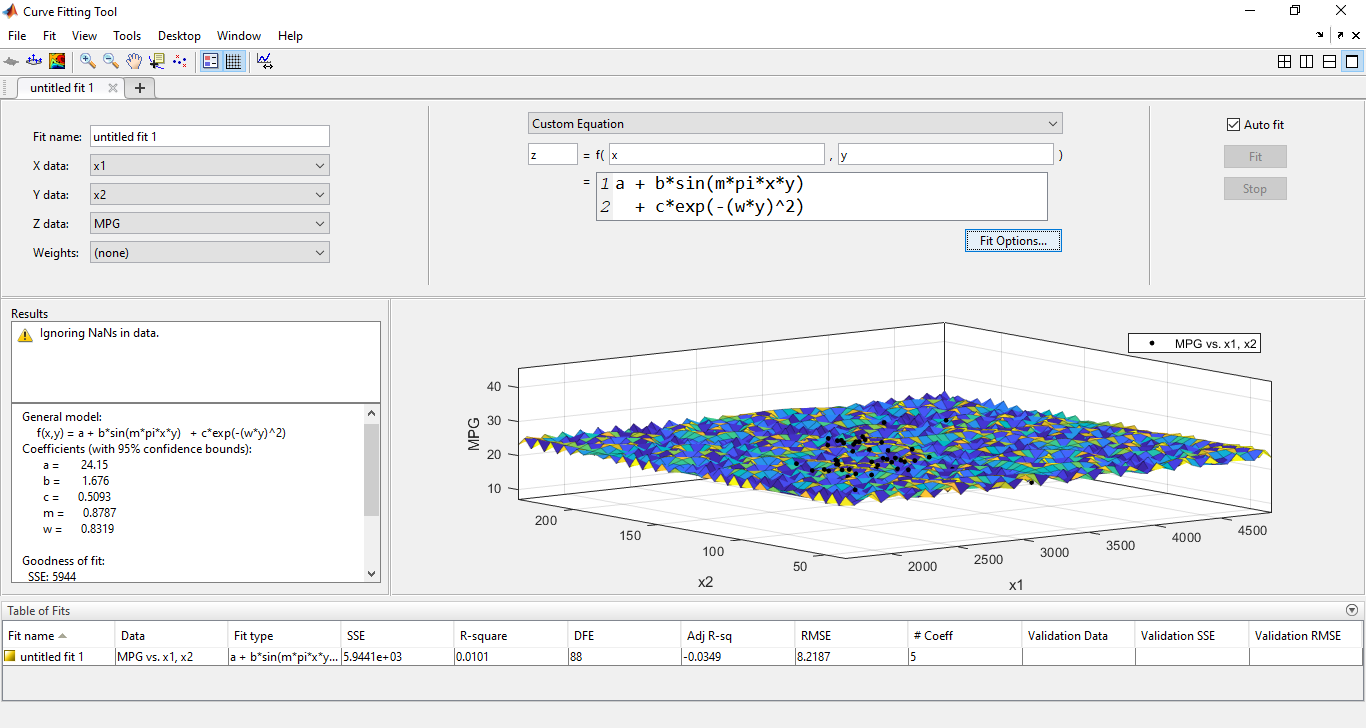
4)非线性拟合_曲线拟合工具箱cftool
对于非线性拟合,需要使用曲线拟合工具箱.在命令窗口输入cftool()打开曲线拟合工具箱.
将需要拟合的数据载入到工作区后,使用 cftool 命令调用工具箱,再选择相应数据和拟合选项进行拟合。
工具条:
第一个“main plot”,拟合曲线
第二个“Residuals plot”,残差图
第三个“Contour plot”,轮廓图
第七个“Data cursor”,进行数据提示
第八个“Exclude outliers”,剔除异常值
拟合选项:
Custom Equations:用户自定义的函数类型;
Exponential:指数逼近,有2种类型, a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x);
Fourier:傅立叶逼近,有8种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w);
Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(-((x-b1)/c1)^2);
Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving;
Polynomial:多形式逼近,有9种类型;
Power:幂逼近,有2种类型,a*x^b 、a*x^b + c;
Rational:有理数逼近,分子、分母各有五种类型;
Smoothing Spline:平滑样条;
Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x + c1)
Weibull:威布尔逼近,只有一种类型a*b*x^(b-1)*exp(-a*x^b)
3.插值
插值的概念:比如给定一组数据,自变量数组X为1*100数据,记录一年中的其中100天的日期编号,数组V为1*100数据,记录这100天中午的气温。插值就是用某种数学方法,找到一个函数(或者一族分段函数),使这个函数穿过所有的100个数据点。然后其余的365-100=265天的数据记作Xq,把xq代入前面得到的函数,算出对应的每天的温度y了。 y=interp1(x,v,xq)



3.1 一维插值
下列函数均与一维插值有关:
| 函数 | 作用 |
|---|---|
interp1(x,v)或interp1(x,v,xq) | 线性插值 |
spline(x,v)或spline(x,v,xq) | 三次样条插值 |
pchip(x,v)或pchip(x,v,xq) | 三次Hermite插值 |
mkpp(breaks,coefs) | 生成分段多项式 |
ppval(pp,xq) | 计算分段多项式的插值结果 |
3.1.1 线性插值interp1

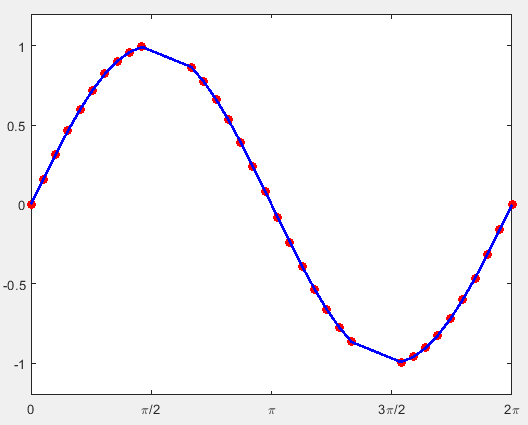
例:基于粗略采样的正弦函数进行插值
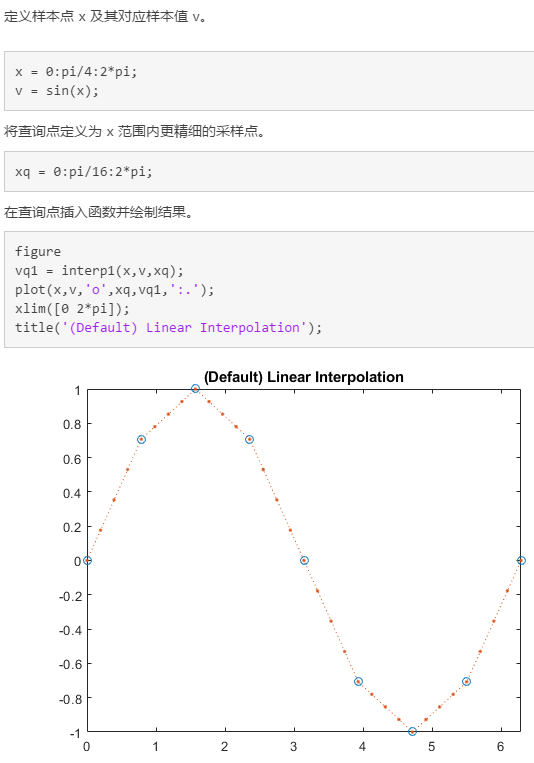
下面例子演示使用interp1(x, v, xq)进行线性插值和使用spline(x, v, xq)进行三次样条插值.各参数意义如下:
x,v: 待插值样本点.
xq: 查询点,函数返回在这些点处的插值结果.
%% 构造分散点
clear
x = linspace(0,2 * pi,40); %在0到2pi之间生成间隔相同的40个点
x_m = x;
x_m([11:13,28:30]) = NaN; %手动将11-13,28-30这6个点变为空,制造下图中的断点
y_m = sin(x_m);
%% 绘制图形
plot(x_m,y_m,'ro','MarkerFaceColor','r');
xlim([0,2*pi]);
ylim([-1.2,1.2]);
box on;
%set(gca,'FontName','symbol','FontSize',16);高版本不需要这一句
set(gca,'XTick',0:pi/2:2*pi);
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'});
%% 内插
m_i = ~isnan(x_m);
%'~':表示取非,这里是将右边判断空值所形成的数组取非后赋值给左边
%isnan():确定哪些数组元素为 NaN
y_i = interp1(x_m(m_i),y_m(m_i),x);
%interp1():一维数据插值(表查找)
hold on;
plot(x,y_i,'-b','LineWidth',2);
注意:
(1)‘~’表示取非,这里是将右边判断空值所形成的数组取非后赋值给左边
(2)TF= isnan(A)返回一个逻辑数组,其中的1(true) 对应A中的NaN元素,0(false) 对应其他元素。如果A包含复数,则isnan(A)中的1对应实部或虚部为NaN值的元素,0对应实部和虚部均非NaN值的元素。

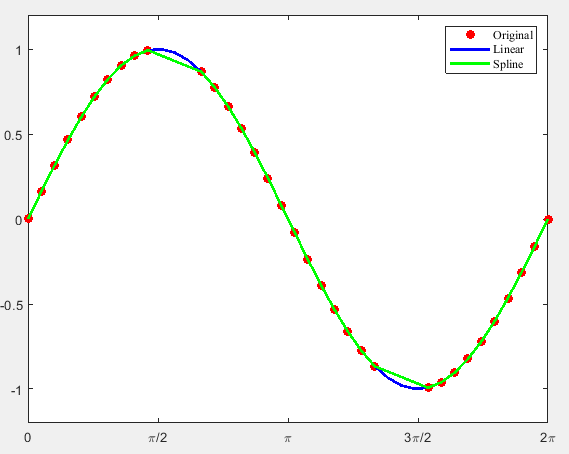
3.1.2 三次样条插值 Spline Interpolation:spline()
x = linspace(0,2 * pi,40);
x_m = x;
x_m([11:13,28:30]) = NaN;
y_m = sin(x_m);
plot(x_m,y_m,'ro','MarkerFaceColor','r'); %绘制散点图
xlim([0,2*pi]);
ylim([-1.2,1.2]);
box on;
%set(gca,'FontName','symbol','FontSize',16); 高版本不需要这一句
set(gca,'XTick',0:pi/2:2*pi);
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'});
%% 内插
m_i = ~isnan(x_m);
y_i1 = spline(x_m(m_i),y_m(m_i),x); %使用内插值线段连接
y_i2 = interp1(x_m(m_i),y_m(m_i),x); %使用样条差值连接
hold on;
plot(x,y_i1,'-b','LineWidth',2);%
plot(x,y_i2,'-g','LineWidth',2);
hold off;
h = legend('Original','Linear','Spline');
set(h,'FontName','Times New Roman');
三次样条插值的原理在每两个样本点之间用两两相切的三次函数曲线来插值.若spline()方法不指定查询点,则返回一个结构体,其中封装了插值三次函数的系数.使用mkpp(breaks, coefs)可以创建一个类似的结构体,使用ppval(pp, xq)可以计算查询点的插值结果.

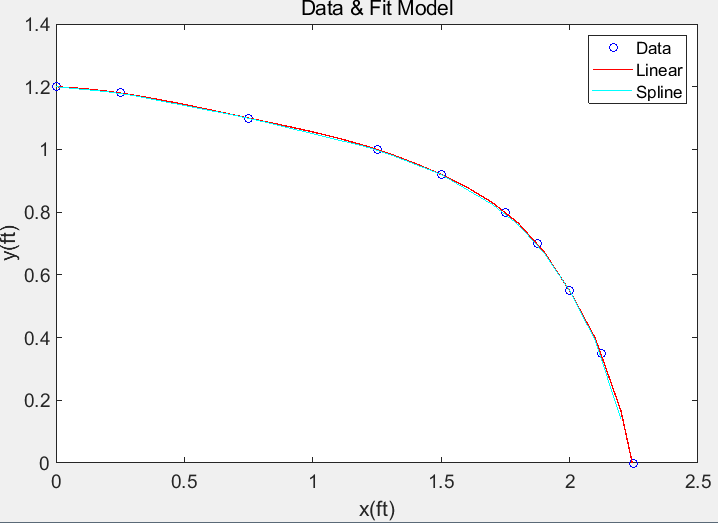
练习:用直线和三次样条拟合数据
x = [0 0.25 0.75 1.25 1.5 1.75 1.875 2 2.125 2.25];
y = [1.2 1.18 1.1 1 0.92 0.8 0.7 0.55 0.35 0];
x_i = 0:0.1:2.5;
hold on
plot(x,y,'bo');%绘制散点图
xlim([0,2.5]);
ylim([0,1.4]);
box on;
y_i1 = interp1(x,y,x_i); %使用内插值线段连接
y_i2 = interp1(x,y,x_i,'spine'); %使用样条差值连接
plot(x_i,y_i2,'r','linewidth',1);
plot(x_i,y_i1,'c');
xlabel('x(ft)');
ylabel('y(ft)');
title('Data & Fit Model');
set(gca,'fontsize',14);
legend('Data','Linear','Spline')
hold off
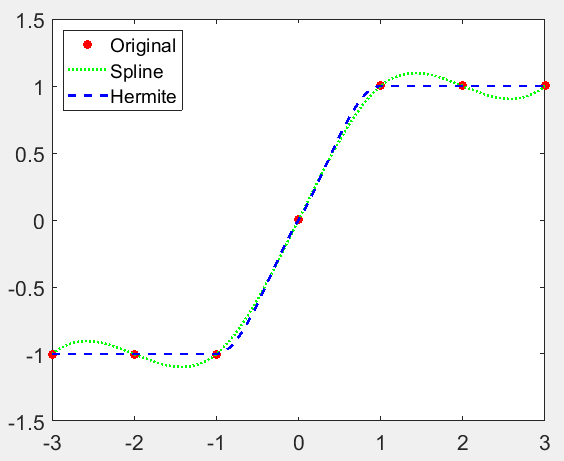
3.1.3 pchip(x, y, xq)
Hermite Polynomial,埃尔米特多项式,可以进行三次Hermite插值,该算法同样以三次函数进行插值,但得到的曲线更平缓.
最大的不同在于,埃尔米特多项式在点和点连接曲线不会片离连接的线段
x = -3:3;
y = [-1 -1 -1 0 1 1 1];
t = -3:.01:3;
s = spline(x,y,t);%spline多项式
p = pchip(x,y,t);%埃尔米特多项式
hold on;
plot(x,y,'ro','MarkerFaceColor','r');
plot(t,s,':g','LineWidth',2);
plot(t,p,'--b','LineWidth',2);
hold off;
box on;
set(gca,'FontSize',16);
h = legend('Original','Spline','Hermite','Location','northwest');
%注意,标的顺序与绘图的先后顺序相同
3.1.4 数据插值的 'method' 选择
3.2 二维插值
使用interp2()可以进行二维插值,向其method参数传入字符串可以指定插值算法.

| 方法 | 说明 | 连续性 |
|---|---|---|
'linear' | (默认)在查询点插入的值基于各维中邻点网格点处数值的线性插值. | C0 |
'spline' | 在查询点插入的值基于各维中邻点网格点处数值的三次插值.插值基于使用非结终止条件的三次样条. | C2 |
'nearest' | 在查询点插入的值是距样本网格点最近的值. | 不连续 |
'cubic' | 在查询点插入的值基于各维中邻点网格点处数值的三次插值.插值基于三次卷积. | C1 |
'makima' | 修改后的Akima三次Hermite插值.在查询点插入的值基于次数最大为3的多项式的分段函数,使用各维中相邻网格点的值进行计算.为防过冲,已改进 Akima 公式. | C1 |
% 构建样本点 xx = -2:.5:2; yy = -2:.5:3; [x,y] = meshgrid(xx,yy); xx_i = -2:0.1:2; yy_i = -2:0.1:3; [x_i,y_i] = meshgrid(xx_i,yy_i); z = x.*exp(-x.^2-y.^2); % 线性插值 subplot(1, 2, 1); z_i = interp2(xx,yy,z,x_i,y_i); surf(x_i,y_i,z_i); hold on; plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on; % 三次插值 subplot(1, 2, 2); z_ic = interp2(xx,yy,z,x_i,y_i, 'spline'); surf(x_i,y_i,z_ic); hold on; plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on;


========================================
========================================
========================================
1. 一元多项式拟合
介绍两种方法:调用系统函数 polyfit,左除法。两种方法结果相同,查看 polyfit 帮助文档,polyfit 函数实际上使用的算法就是左除。

clear;clc;close all;
% 产生拟合数据
rng('default');
x = 1:50;
y = -0.3*x + randn(1, 50);
% 用 1 次多项式来拟合
p = polyfit(x, y, 1);
% 计算拟合值
y1 = polyval(p, x);
% 绘图
plot(x,y,'o', x, y1)
legend('data','linear fit')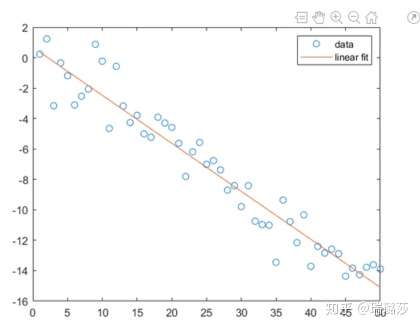
% 用左除的方法 p1 = [x', ones(length(x), 1)] \ y'; % 结果对比 disp(num2str(1000000*[p; p1']));
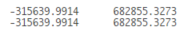
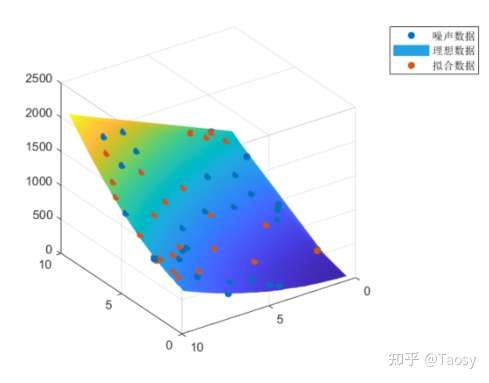
2. 二元多项式拟合
基于一元多项式拟合的左除方法,进一步推广到二元多项式拟合,对比左除法和调用系统函数 lsqcurvefit 结果,两者基本一致。
clear; clc; close all; % 曲面方程:f(x,y) = a20*x.^2 + a02*y.^2 + a11*x.*y + a10*x + a01*y + a00 x = 0.1 : 0.1 : 5; y = 0.1 : 0.1 : 5; [X, Y] = meshgrid(x, y); % 建立曲面模型,假设未知参数都是 1 Z = X.^2 + Y.^2 + X.*Y + X + Y + 1; % 绘制模型曲面 surf(X, Y, Z); shading interp

% 添加噪声
rng('default');
ratio = 1;
Z1 = Z + ratio*randn(size(Z));
% 随机选择 100 个点来做拟合
xPos = randi(50, 100, 1);
yPos = randi(50, 100, 1);
xfit = x(xPos)';
yfit = y(yPos)';
zfit = zeros(100, 1);
for i = 1:100
zfit(i) = Z1(xPos(i), yPos(i));
end
% 绘制带有噪音的模型曲面和用来拟合的离散点
surf(X, Y, Z1);
shading interp
hold on
scatter3(xfit, yfit, zfit, 50, 'MarkerFaceColor', [0 0 0]);
hold off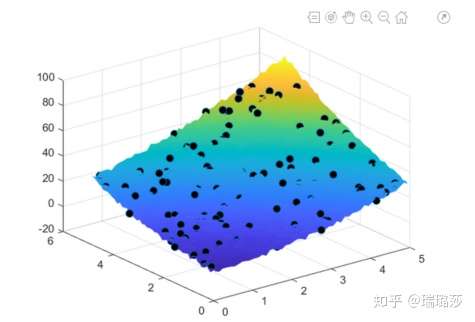
% 两种方式求解
% 1. 用 lsqcurvefit 函数求解
func = @(var,x) var(1)*x(:,1).^2 + var(2)*x(:,2).^2 + var(3)*x(:,1).*x(:,2) + var(4)*x(:,1) + var(5)*x(:,2) + var(6);
val = lsqcurvefit(func, rand(1, 6), [xfit, yfit], zfit);
% 拟合值
zFit = func(val, [xfit, yfit]);
% 2. 用左除的方法求解
xfit2 = xfit.^2;
yfit2 = yfit.^2;
xyfit = xfit.*yfit;
A = [xfit2, yfit2, xyfit, xfit, yfit, ones(100, 1)];
val2 = A \ zfit;
% 拟合值
zFit2 = func(val2, [xfit, yfit]);
% 绘制拟合点结果
plot(zfit, zFit, 'o', zfit, zFit2, '*');
legend('lsqcurvefit', 'left-divide')
xlabel('data');
ylabel('fitting');
title('data VS fitting');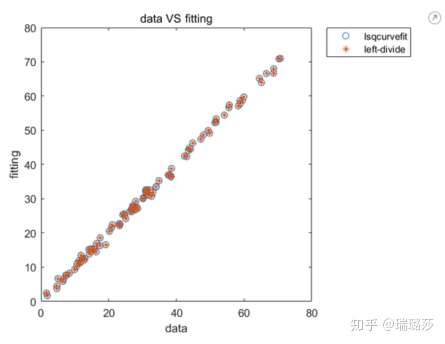
% 结果对比 disp(num2str(1000000*[val; val2']));

【秘籍】
了解一元多项式拟合的算法本质,推广到多元多项式形式,对于这类问题,左除是一个很好方法。
=============================================
重点介绍基于最小二乘的 Levenberg-Marquardt 实现方法和代码实现
线性拟合
多项式拟合
多元线性拟合
多元多项式拟合
非线性拟合
代码仓库:
线性拟合
模型: ;
已知一系列 和
,求解未知参数
和
;
求解方法:polyfit、左除;
多项式拟合
模型: ;
已知一系列 和
,求解未知参数
;
求解方法:polyfit、左除;
多元线性拟合
模型: ;
求解方法:regress、左除;
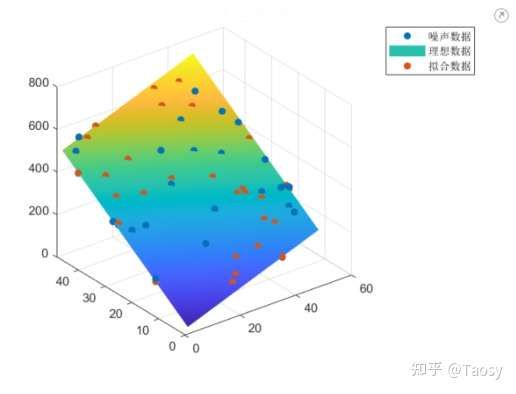
多元多项式拟合
模型: ;
求解方法:lsqcurvefit、nlinfit、regress、左除;
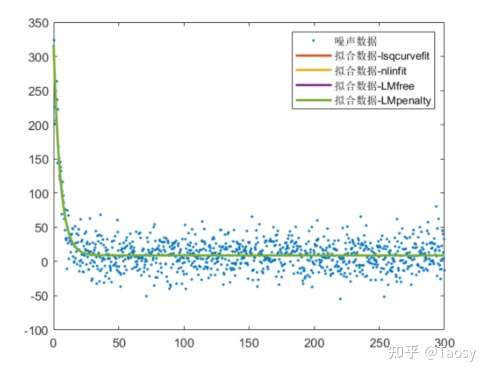
非线性拟合
模型: ;
求解方法:lsqcurvefit、nlinfit、高斯牛顿法、Levenberg-Marquardt;
模型:
残差:
目标函数:
模型函数分别对A、B、C求偏导数得到 Jacobi 矩阵:
目标函数对A、B、C求偏导数得到梯度矩阵:
计算目标函数的 Hessian 矩阵:
高斯牛顿法计算更新步长:
Levenberg-Marquardt 更新步长和正则化参数:
障碍罚函数约束,构造一个辅助函数来求解最优化问题,假设约束条件为 A、B、C 大于 0:
原目标函数变为:
迭代步长:
无约束最优化,求解问题变换形式,然后按照正常方式求解:
代码实现部分
clear;clc;close all;
%%%%%%%%%%%%%%%%%%%% 线性拟合 %%%%%%%%%%%%%%%%%%%%
% 保证结果可重复
rng('default');
% 生成数据
len = 20;
x = linspace(0, 10, len);
y = 2*x + 2;
% 添加噪声
y_noise = y + randn(1, len);
% 调用 polyfit 函数
p = polyfit(x, y_noise, 1)
% 拟合结果 y_fit = polyval(p, x); % 左除 pp = [x', ones(len, 1)] \ y_noise'

% 显示结果
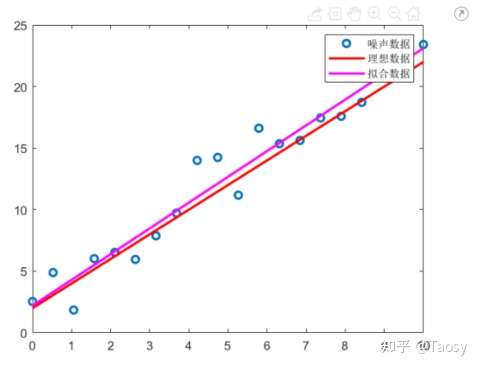
figure;
plot(x, y_noise, 'o', 'LineWidth', 2);
hold on
plot(x, y, 'r', 'LineWidth', 2);
plot(x, y_fit, 'm', 'LineWidth', 2);
hold off
legend('噪声数据', '理想数据', '拟合数据');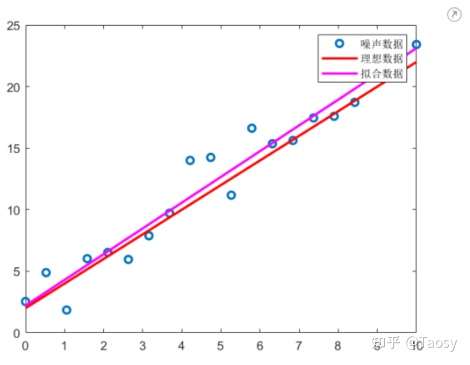
%%%%%%%%%%%%%%%%%%%% 多项式拟合 %%%%%%%%%%%%%%%%%%%%
% 保证结果可重复
rng('default');
% 生成数据
len = 40;
x = linspace(-10, 10, len);
y = 2*x.^2 + 2*x + 2;
% 添加噪声
y_noise = y + 5*randn(1, len);
% 调用 polyfit 函数
p = polyfit(x, y_noise, 2)
% 拟合结果 y_fit = polyval(p, x); % 左除 pp = [x.^2', x', ones(len, 1)] \ y_noise'

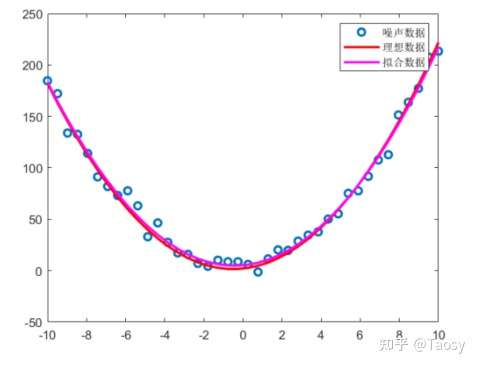
% 显示结果
figure;
plot(x, y_noise, 'o', 'LineWidth', 2);
hold on
plot(x, y, 'r', 'LineWidth', 2);
plot(x, y_fit, 'm', 'LineWidth', 2);
hold off
legend('噪声数据', '理想数据', '拟合数据');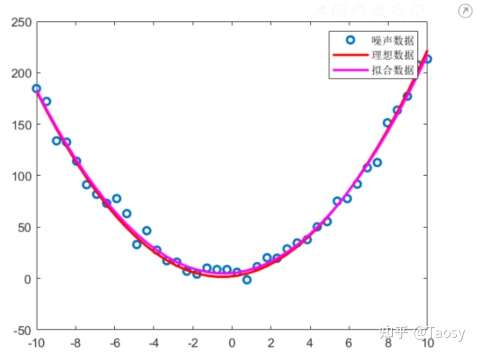
%%%%%%%%%%%%%%%%%%%% 多元线性拟合 %%%%%%%%%%%%%%%%%%%%
% 保证结果可重复
rng('default');
% 生成数据
len = 50;
x = randi(50, len, 1);
y = randi(50, len, 1);
f = 5*x + 10*y + 2;
% 添加噪声
f_noise = f + 5*randn(len, 1);
% 调用 regress 函数
X = [x, y, ones(len, 1)];
p = regress(f_noise, X)
% 拟合结果 f_fit = p(1)*x + p(2)*y + p(3); % 左除 pp = X \ f_noise

% 显示结果
figure;
scatter3(x, y, f_noise, 'filled');
hold on
[xx, yy] = meshgrid(x, y);
surf(xx, yy, 5*xx + 10*yy + 2);
shading interp
scatter3(x, y, f_fit, 'filled');
hold off
legend('噪声数据', '理想数据', '拟合数据');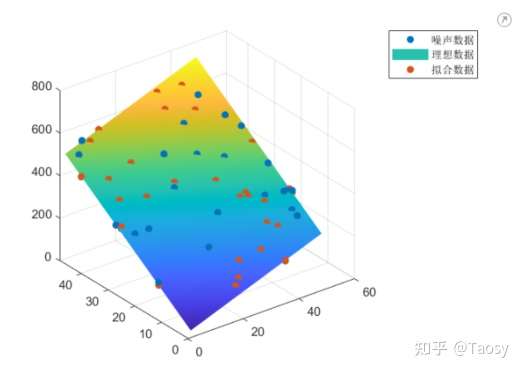
%%%%%%%%%%%%%%%%%%%% 多元多项式拟合 %%%%%%%%%%%%%%%%%%%%
% 保证结果可重复
rng('default');
% 生成数据
len = 50;
x = randi(50, len, 1) / 5;
y = randi(50, len, 1) / 5;
fun = @(p, x, y) p(1)*x.^2 + p(2)*y.^2 + p(3)*x.*y + p(4)*x + p(5)*y + p(6);
p0 = [5, 10, 5, 10, 10, 2];
f = fun(p0, x, y);
% 添加噪声
f_noise = f + 10*randn(len, 1);
[xx, yy] = meshgrid(x, y);
ff = fun(p0, xx, yy);
% 调用 lsqcurvefit
func = @(var, x) var(1)*x(:,1).^2 + var(2)*x(:,2).^2 + var(3)*x(:,1).*x(:,2) + var(4)*x(:,1) + var(5)*x(:,2) + var(6);
p = lsqcurvefit(func, ones(1, 6), [x, y], f_noise)
% 拟合结果 f_fit = func(p, [x, y]); % 调用 nlinfit pp = nlinfit([x, y], f_noise, func, ones(1, 6))

% 调用 regress X = [x.^2, y.^2, x.*y, x, y, ones(len, 1)]; ppp = regress(f_noise, X)

% 左除 pppp = X \ f_noise

% 显示结果
figure;
scatter3(x, y, f_noise, 'filled');
hold on
[xx, yy] = meshgrid(x, y);
surf(xx, yy, fun(p, xx, yy));
shading interp
view([-145 -30]);
scatter3(x, y, f_fit, 'filled');
hold off
legend('噪声数据', '理想数据', '拟合数据');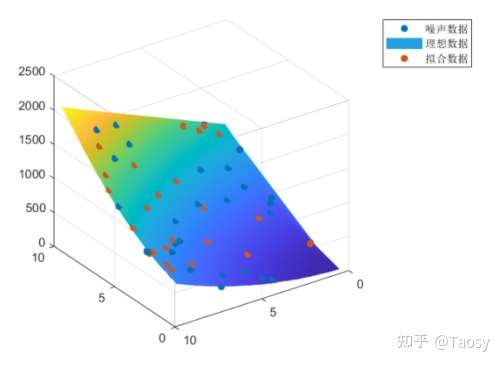
%%%%%%%%%%%%%%%%%%%% 非线性拟合 %%%%%%%%%%%%%%%%%%%%
% 保证结果可重复
rng('default');
% 生成数据
len = 1000;
x = linspace(0.1, 300, len)';
y = 300*exp(-x/5) + 10;
% 添加噪声
y_noise = y + 20*randn(len, 1);
% 调用 lsqcurvefit
func = @(p, x) p(1)*exp(-x/p(2)) + p(3);
% 选择合适的初始值
p0 = [100, 2 1];
p = lsqcurvefit(func, p0, x, y_noise)
% 拟合结果 y_fit_lsq = func(p, x); % 调用 nlinfit pp = nlinfit(x, y_noise, func, p0)

y_fit_nlin = func(pp, x); % Levenberg-Marquardt 求解 p1 = LSFittingExpFree(x, y_noise)

p2 = LSFittingExpPenalty(x, y_noise)

fit1 = func(p1, x);
fit2 = func(p2, x);
% 显示结果
figure;
plot(x, y_noise, '.', 'LineWidth', 2);
hold on
plot(x, y_fit_lsq, 'LineWidth', 2);
plot(x, y_fit_nlin, 'LineWidth', 2);
plot(x, fit1, 'LineWidth', 2);
plot(x, fit2, 'LineWidth', 2);
hold off
legend('噪声数据', '拟合数据-lsqcurvefit', '拟合数据-nlinfit', '拟合数据-LMfree', '拟合数据-LMpenalty');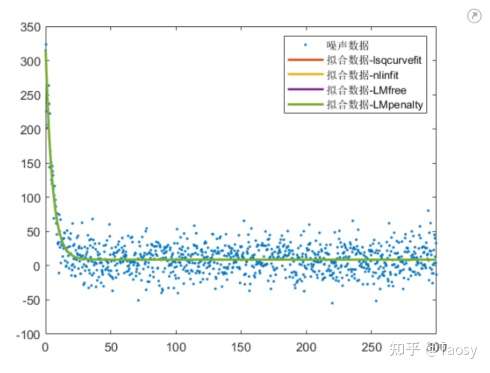
function result = LSFittingExpFree(x, y)
% Levenberg_Marquardt LS Fitting
% 按列排
x = x(:);
y = y(:);
M = length(x);
% Least Squares Minimization
rng('default');
% 初始值
a = sqrt(rand);
b = sqrt(rand);
c = sqrt(rand);
% 变量个数
nParam = 3;
% 残差
r = y - (a^2 * exp(-x / b^2) + c^2);
% 目标函数
f = r'*r;
% 正则化因子初值
lambda = 1;
% 迭代次数
it = 0;
% 更新标记
updateFlag = true;
% 最大迭代次数
maxIter = 100;
% 迭代计算
while it < maxIter
it = it + 1;
if updateFlag
Ja = 2 * a * exp(-x / b^2);
Jb = 2 * a^2 * x .* exp(-x / b^2) / b^3;
Jc = 2 * c * ones(M, 1);
J = [Ja, Jb, Jc];
g = -2 * J' * r;
H = 2 * (J'*J);
end
Hess = H + lambda * eye(nParam);
s = -Hess \ g;
a1 = a + s(1);
b1 = b + s(2);
c1 = c + s(3);
r1 = y - (a1^2 * exp(-x / b1^2) + c1^2);
f1 = r1'*r1;
fdr = (f - f1) / f;
if fdr > 0
a = a1;
b = b1;
c = c1;
f = f1;
r = r1;
lambda = 0.1 * lambda;
updateFlag = true;
else
lambda = 10 * lambda;
updateFlag = false;
end
if max(abs(s)) < 1e-6
disp(['达到收敛条件,迭代次数:' num2str(it)]);
break;
elseif it == maxIter
disp('达到最高迭代次数,可能不收敛;');
end
end
result = [a^2, b^2, c^2];
end
function result = LSFittingExpPenalty(x, y)
% Levenberg_Marquardt LS Fitting
% 按列排
x = x(:);
y = y(:);
M = length(x);
% 初始值
a0 = rand;
b0 = rand;
c0 = rand;
% 变量个数
nParam = 3;
% 残差
r0 = y - (a0 * exp(-x / b0) + c0);
% 障碍罚函数的收缩系数个数
numLoop = 5;
% 最大迭代次数
maxIter = 100;
% 障碍罚函数收缩系数
mu = 10;
k = 0;
while k < numLoop
k = k + 1;
mu = mu * 0.1;
% Least Squares Minimization
a = a0;
b = b0;
c = c0;
r = r0;
% 目标函数值
f = r'*r - mu * (log(a) + log(b) + log(c));
% 正则化因子初值
lambda = 1;
% 迭代次数
it = 0;
% 更新标记
updateFlag = true;
% 迭代计算
while it < maxIter
it = it + 1;
if updateFlag
Ja = exp(-x / b);
Jb = a * x .* exp(-x / b) / b^2;
J = [Ja, Jb, ones(M, 1)];
g = -2 * J' * r - mu * [1/a; 1/b; 1/c];
H = 2 * (J'*J) - mu * diag([-1/a^2, -1/b^2, -1/c^2]);
end
s = -(H + lambda * eye(nParam)) \ g;
while a + s(1) < 0 || b + s(2) < 0 || c + s(3) < 0
s = 0.5 * s;
end
a1 = a + s(1);
b1 = b + s(2);
c1 = c + s(3);
r1 = y - (a1 * exp(-x / b1) + c1);
f1 = (r1'*r1) - mu * (log(a1) + log(b1) + log(c1));
fdr = (f - f1) / f;
if fdr > 0
a = a1;
b = b1;
c = c1;
f = f1;
r = r1;
lambda = 0.1 * lambda;
updateFlag = true;
else
lambda = 10 * lambda;
updateFlag = false;
end
if max(abs(s)) < 1e-6
disp(['达到收敛条件,迭代次数:' num2str(it)]);
break;
elseif it == maxIter
disp('达到最高迭代次数,可能不收敛;');
end
end
history.a(k) = a;
history.b(k) = b;
history.c(k) = c;
history.ssr(k) = r'*r;
end
[~, minIndex] = min(history.ssr);
a = history.a(minIndex);
b = history.b(minIndex);
c = history.c(minIndex);
result = [a, b, c];
end=============================================
参考资料:
(1)https://www.bilibili.com/video/BV17B4y1u7b9?spm_id_from=333.999.0.0