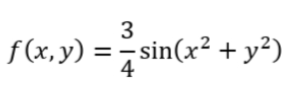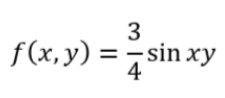1、统计图表常用绘图函数:area(x,y) , stem(x,y) , stairs(x,y)
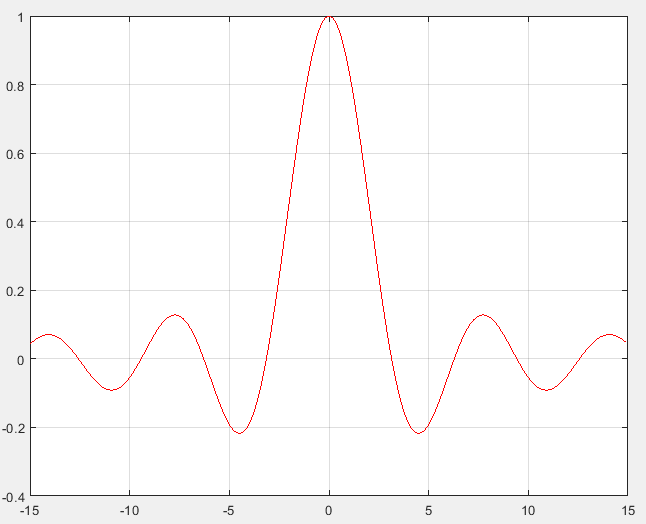
作为对比,先来看普通的plot(x,y)绘图效果
x=-15:0.13:15;
y=(sin(x)./x);
plot(x,y,'r')
grid on
area(x,y) 面积图
x=-15:0.13:15;
y=(sin(x)./x);
area(x,y)
grid on

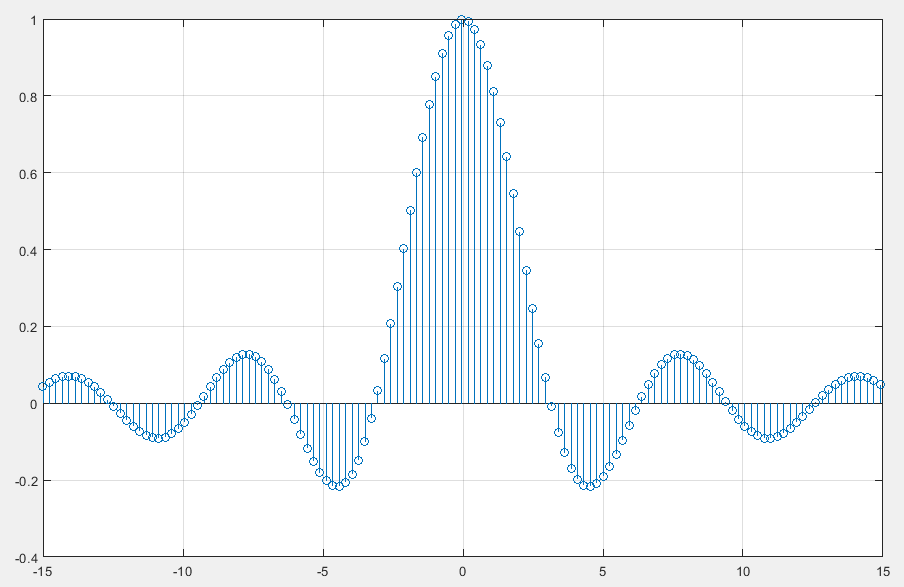
stem(x,y) : 离散序列针状图(火柴棍图):
x=-15:0.23:15;
y=(sin(x)./x);
stem(x,y)
grid on
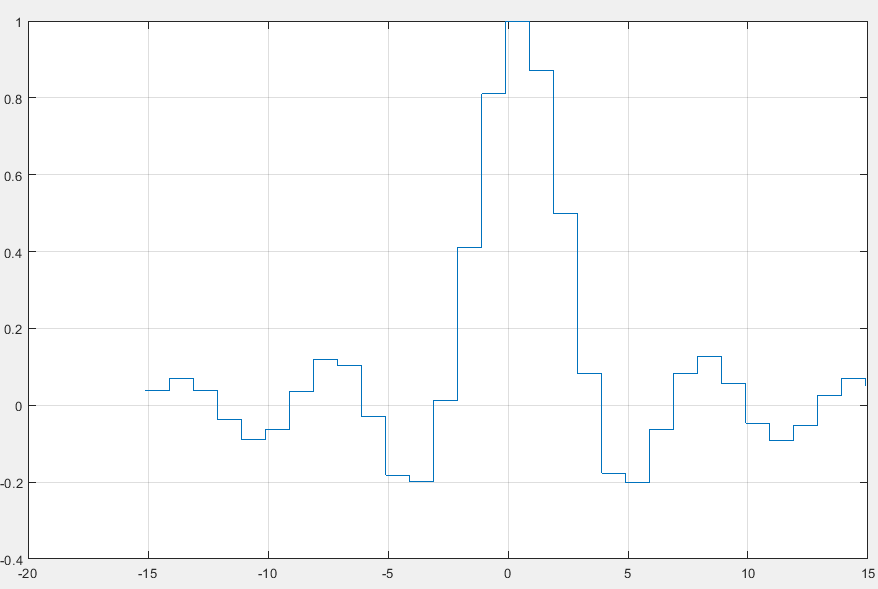
stairs(x,y): 阶梯图
x=-15.1 : 1 :15;
y=(sin(x)./x);
stairs(x,y)
grid on
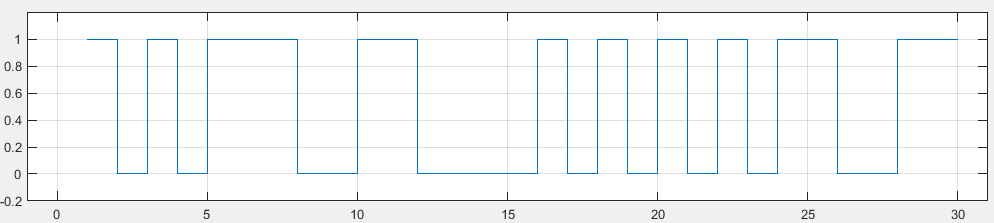
可以利用stairs(x)绘制二进制波形图。
x=randi( [0,1],1,30 );
stairs(x)
grid on
axis( [-1 31 -0.2 1.2] )
hist:直方图(累计分布图)
hist,直方图也被称为频数直方图,它用来显示数据集的分布情况。在MATLAB中绘制直方图的函数是hist,用法是hist(y,x),表示以向量x的各个元素为统计范围,绘制y的分布情况。
用法1:n=hist(Y); 默认用法,把数据均匀分成10个区间进行统计,并绘制频数分布图。
y=randn(1,10000);
n=hist(y) %返回10个区间中,每个区间内的数据的数量。
hist(y) %绘制直方图。
默认十个等间隔区间,并返回每个范围内的y的元素个数作为一行向量,如下图:
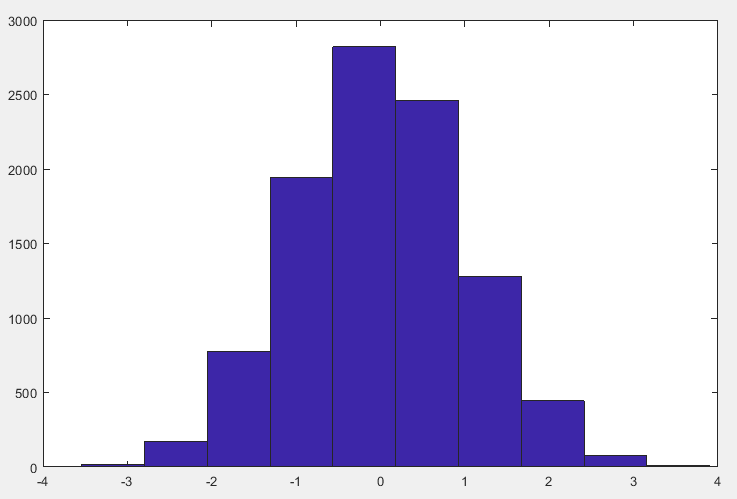

用法2:n=hist(Y,M); 把数据分成M个均匀区间进行统计。
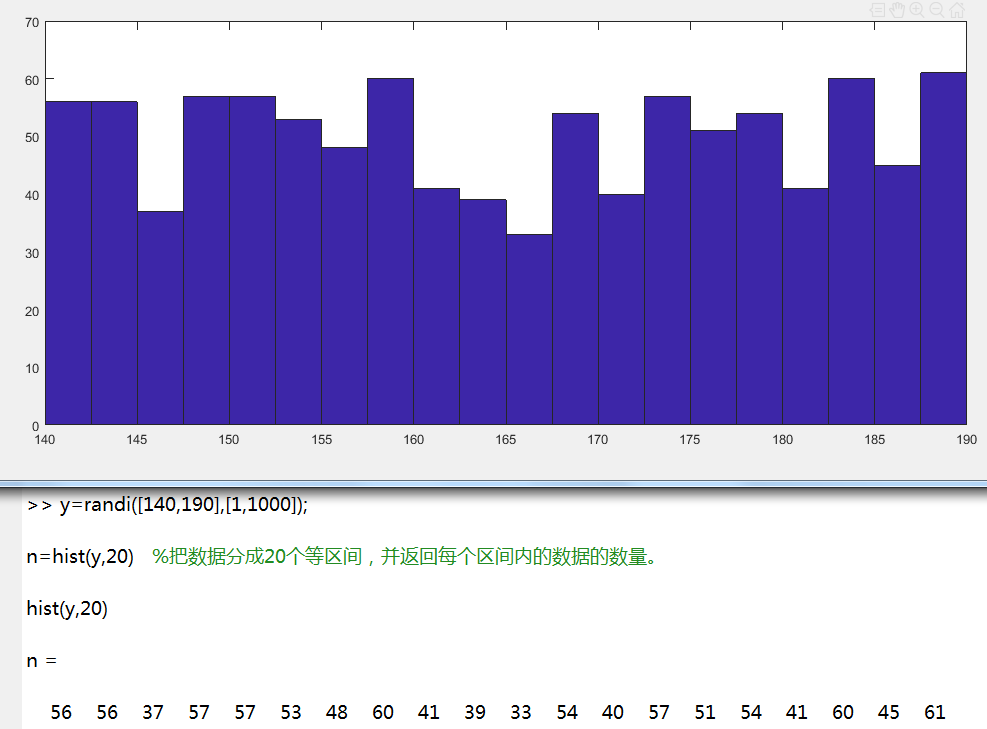
y=randi([140,190],[1,1000]); %随机生产身高分布
%把数据分成20个等区间,并返回每个区间内的数据的数量。
hist(y,20)
用法3:n=hist(y,x); 把数据按照数组x的中的每个值为中心,进行频数统计。
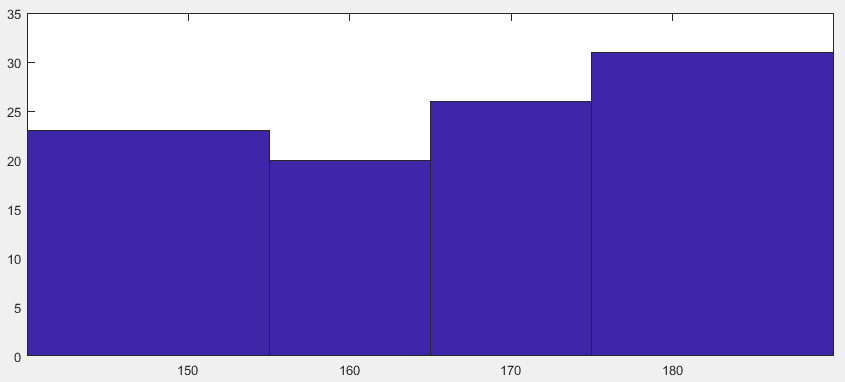
y=randi( [140,190] ,[1,100] ); %随机生产身高分布
x=[150, 160, 170, 180];
hist(y,x) %把数据按照x中的元素为中心,进行频数统计,返回每个区间内的数据数量
%第1个分组是(-inf,155],第2个是(155,165], 第3个是(165,175),第4个是(175,inf)
Histogram() 直方图

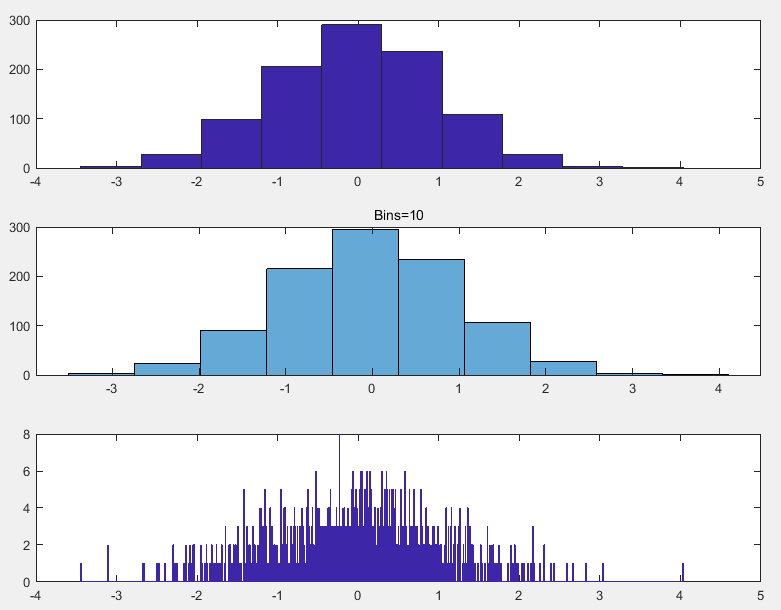
clear;
y=randn(1,1000); %成生一个1 *1000 的符号正态随机的矩阵
subplot(3,1,1);
hist(y,10); %分成10个BIN,Y轴表示在每个BIN中的元素个数
subplot(3,1,2);
histogram(y,10);
title('Bins=10');
subplot(3,1,3);
hist(y,1000);
饼图:pie(X,explode)
使用pie()和pie3()
可以绘制二维和三维的饼图.向其传入一个bool向量表示每一部分扇区是否偏移.
pie(X,explode) 将扇区从饼图偏移一定位置。explode 是一个由与 X 对应的零值和非零值组成的向量或矩阵。pie 函数仅将对应于 explode 中的非零元素的扇区偏移一定的位置。如果 X 为 categorical 数据类型,则 explode 可以是由对应于类别的零值和非零值组成的向量,或者是由要偏移的类别名称组成的元胞数组。通过将对应的 explode 元素设置为 1 来偏移第饼图扇区。
clear;
a=[10 5 20 30];
subplot(2,2,1); pie(a);
subplot(2,2,2); pie(a,[0 0 0 1]);
subplot(2,2,3); pie3(a,[0 0 0 1]);
subplot(2,2,4); pie(a,[1 1 1 1]);

bar()/bar3()/barh()/bar3h()
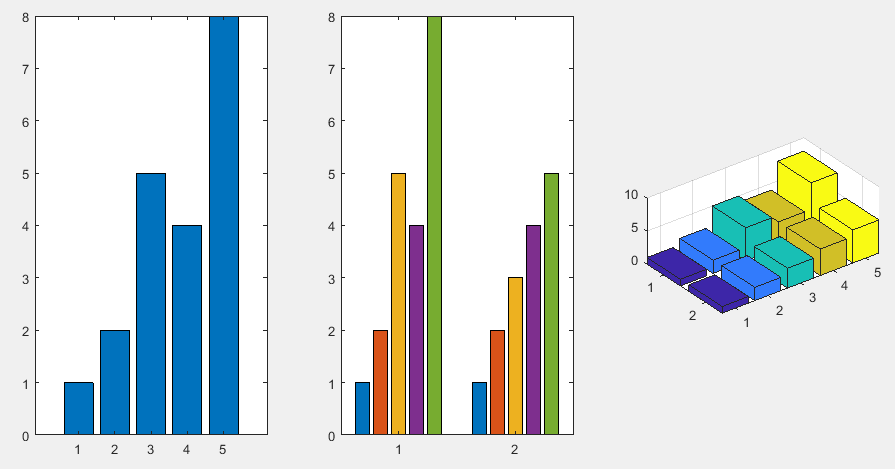
x=[1 2 5 4 8]; y=[x;1:5];
subplot(1,3,1); bar(x); %x 中的每个元素对应一个条形。
subplot(1,3,2); bar(y); %y 中的每个元素对应一个条形。如果 y 是矩阵,则 bar 根据 y 中的行对条形分组。
subplot(1,3,3); bar3(y); %会生成三维图
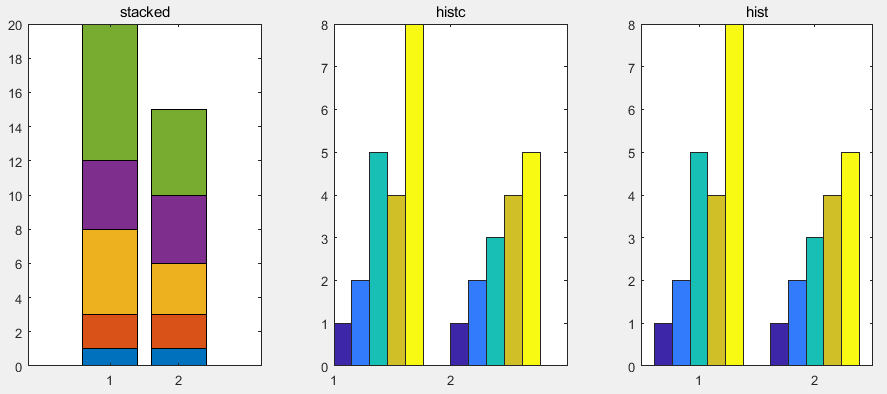
x=[1 2 5 4 8]; y=[x;1:5];
subplot(1,3,1); bar(y,'stacked');
title('stacked');
subplot(1,3,2); bar(y,'histc');
title('histc');
subplot(1,3,3); bar(y,'hist');
title('hist');
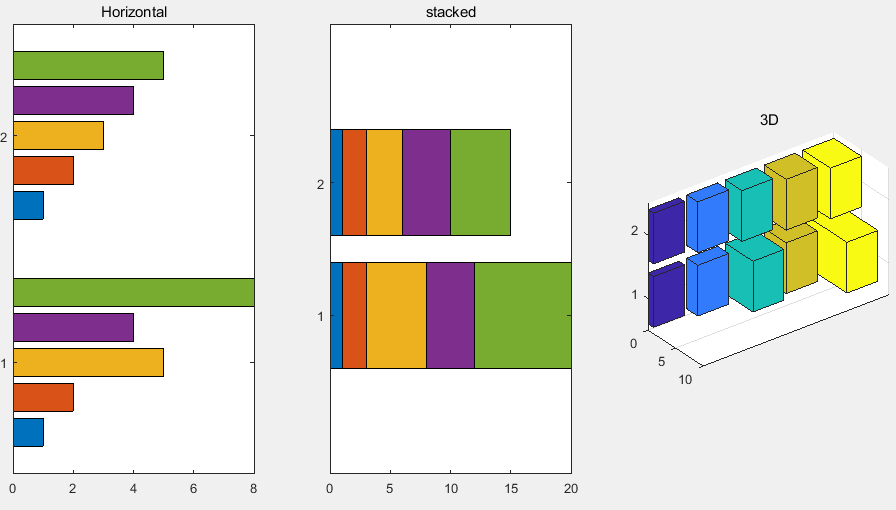
x=[1 2 5 4 8]; y=[x;1:5];
subplot(1,3,1);
barh(y);
title('Horizontal');
subplot(1,3,2);
barh(y,'stacked');
title('stacked');
subplot(1,3,3);
bar3h(y);
title('3D');
scatter()散点图
语法
scatter(x,y) 在向量 x和 y指定的位置创建一个包含圆形的散点图。该类型的图形也称为气泡图。
scatter(x,y,sz)指定圆大小。要绘制大小相等的圆圈,请将 sz指定为标量。要绘制大小不等的圆,请将 sz指定为长度等于 x和 y的长度的向量。
scatter(x,y,sz,c)指定圆颜色。要以相同的颜色绘制所有圆圈,请将 c 指定为颜色名称或 RGB 三元组。要使用不同的颜色,请将 c指定为向量或由 RGB 三元组组成的三列矩阵。scatter(___,'filled') 填充圆形。可以将 'filled'选项与前面语法中的任何输入参数组合一起使用。
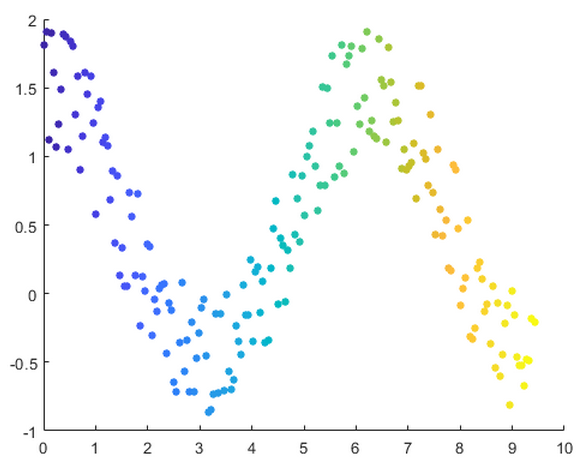
例:创建散点图
创建 x 为 0 和
之间的 200 个等间距值。创建 y为带随机干扰的余弦值。然后,创建一个散点图。
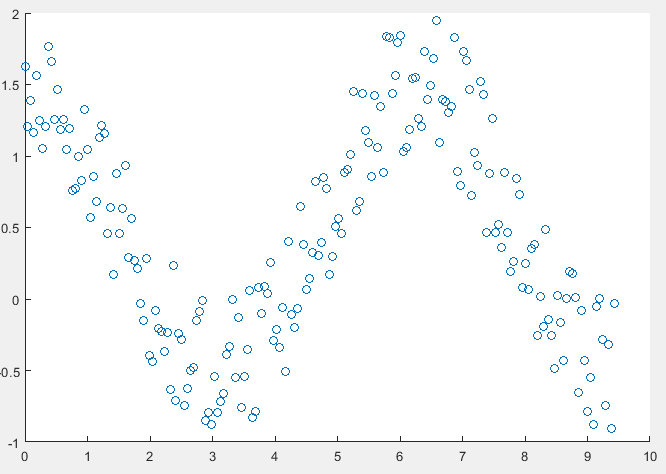
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
scatter(x,y)
改变圆圈大小
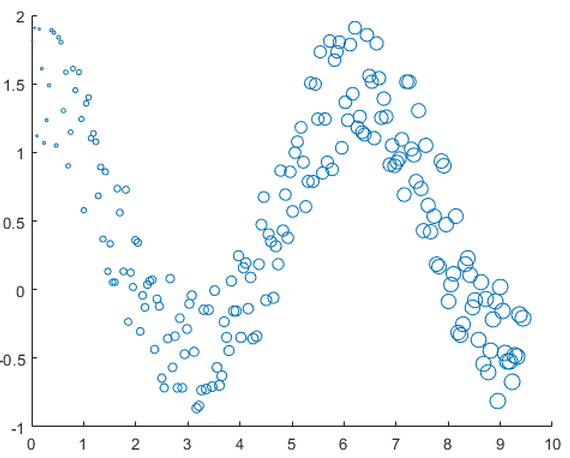
使用大小不同的圆圈创建一个散点图。以平方磅为单位指定大小
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
sz = linspace(1,100,200);
scatter(x,y,sz)
改变圆圈颜色
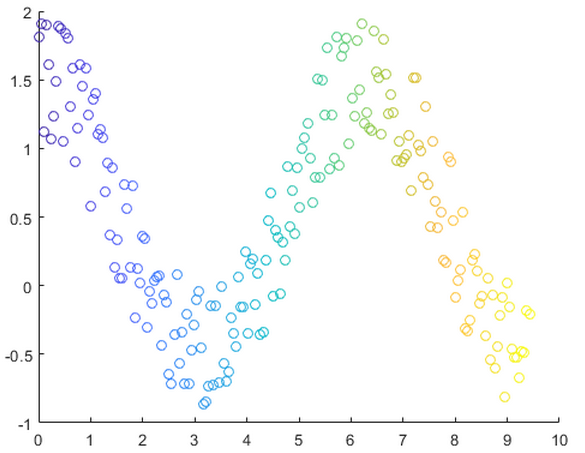
创建一个散点图并改变圆圈的颜色。
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
c = linspace(1,10,length(x));
scatter(x,y,[],c)
填充标记
创建一个散点图并填充标记。
scatter使用标记边的颜色填充每个标记。
x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);
sz = 25;
c = linspace(1,10,length(x));
scatter(x,y,sz,c,'filled')
其它统计图表:
boxplot()load carsmallboxplot(MPG, Origin);
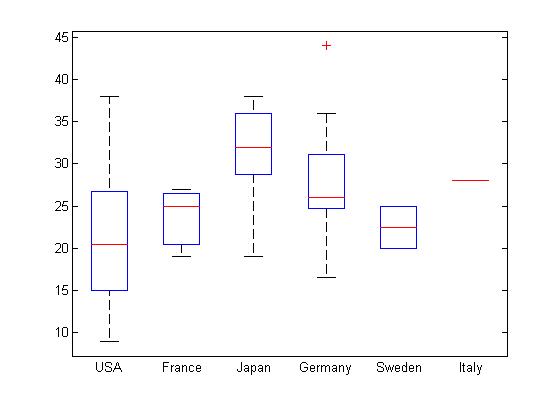
errorbar()
x=0:pi/10:pi; y=sin(x);e=std(y)*ones(size(x));errorbar(x,y,e)
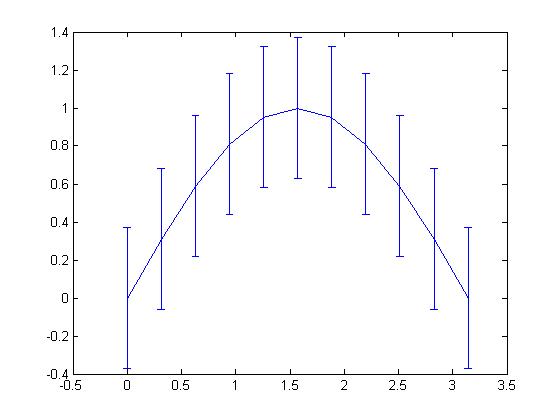
矢量图1:罗盘图compass()
compass(x,y):x,y是n维向量,显示n个箭头,箭头的起点为原点,箭头位置为(x(i),y(i)).
compazz(z):参量z为n维复数向量,命令显示n个箭头,箭头起点为原点,箭头位置为(real(z),image(z))。
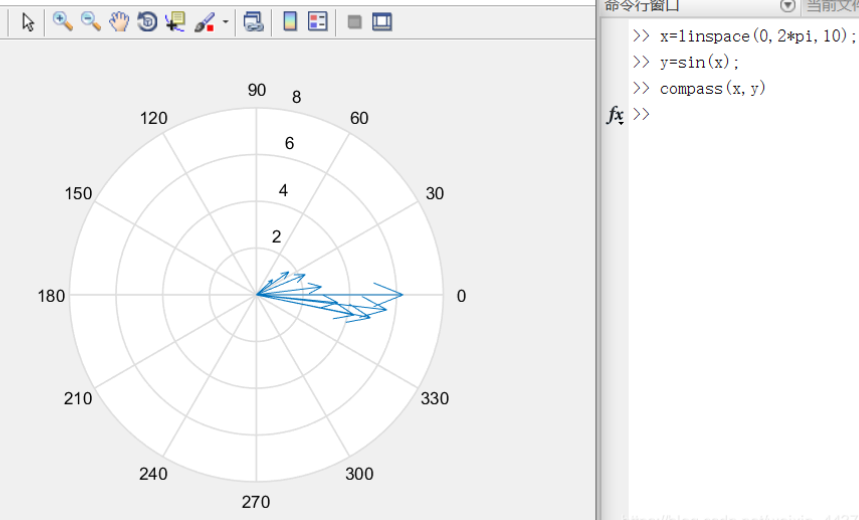
矢量图2:箭头图(速度图)quiver()


2、绘制简单动画效果图
(1)使用pause命令实现逐点查看绘图过程:
pause(a)表示程序暂停a秒后继续执行;
如果只用 pause,不加参数a,这样的意思是程序暂停,按任意键程序继续执行。
比较下面两段程序:
x=linspace(0,7,70);
y=sin(x);
figure()
for ii=1:70
plot(x(ii),y(ii),'r*')
axis([0 8 -1.2 1.2])
grid on
hold on %思考一下,这里为什么要加hold on命令,如果不加会如何?
pause %按任意键程序继续执行
end
x=linspace(-12,12,101);
y=(sin(x)./x);
figure()
for ii=1:101
plot(x(ii),y(ii),'r*')
axis([-13 13 -0.3 1.1])
grid on
hold on
pause(0.1) %程序暂停0.1秒后继续执行
end
Lissajous 曲线的动画演示
随着常数 m 和 n 的变化,参数方程 x = sin(m · t), y = sin(n · t) 将会画出一系列漂亮的曲线。法国物理学家 Jules Antoine Lissajous 曾在 1857 年研究过这类曲线,因此人们把它叫做 Lissajous 曲线。
这个动画展示的是 m = 13, n = 18 时的 Lissajous 曲线。
请编程实现。
t=0:0.001:7;
x=sin(13*t);
y=sin(18*t);
plot(x,y)
(2)质点动画——动态彗星图:
质点动画由comet、comet3函数产生质点动画,分别对应二维和三维坐标下的质点。首先求解出质点完整的运动轨迹坐标x,y(三维时还有z),将x,y作为输入参数使用comet或comet3直接绘制动点。
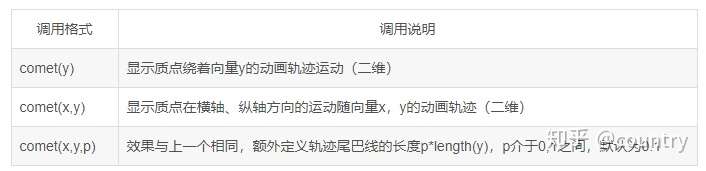
comet3函数的使用方法与comet相似。
2维的comet
例1:
t = 0 : 0.01 : 2*pi ;
x = cos(2*t).*(cos(t).^2) ;
y = sin(2*t).*(sin(t).^2) ;
comet(x,y) ;
例2:
clf;
clear;
grid on;
vx = 100*cos(1/4*pi);
vy = 100*sin(1/4*pi);
t = 0:0.02:15;
dx = vx*t;
dy = vy*t-9.8*t.^2/2;
comet(dx, dy);
3维的comet3
t = -10*pi : pi/250 : 10*pi ;
x = (cos(2*t).^2).*sin(t) ;
y = (sin(2*t).^2).*cos(t) ;
comet3(x,y,t) ;
%首先可以构建多个运行轨迹,之后取各轨迹上一个点作为动点,通过不断更新点的位置,就可以得%到多沿条曲线运动点的动画;以一个圆轨道和椭圆轨道上两个运动点为例,代码如下:
% 沿曲线线运动的多个图形动画
figure
% 圆轨迹
t1 = linspace(0,2*pi,200);
x1 = cos(t1);y1 = sin(t1);
plot(x1,y1,'LineWidth',1.5)
hold on
% 椭圆轨迹
t2 = linspace(0,4*pi,400);
x2 = 3*cos(t2);y2 = 1.5*sin(t2);
plot(x2,y2,'LineWidth',1.5)
xlim([-4,4])
axis equal,axis manual,axis off
ax = gca;
hold on
% 圆轨迹上的运动点
p1 = plot(x1(1),y1(1),'ro','MarkerFaceColor','r','MarkerSize',10);
% 椭圆轨迹上的运动点
p2 = plot(x2(1),y2(1),'go','MarkerFaceColor','g','MarkerSize',14);
hold off
% 绘制多体运动动画
for k = 1:length(x1)
p1.XData = x1(k);p1.YData = y1(k);
p2.XData = x2(2*k-1);p2.YData = y2(2*k-1);
drawnow
end
首先,创建运动轨迹,并限定显示区域,使用hgtransform 函数创建变换对象组父级作为运动轨迹;之后绘制运动的图形,使用makehgtform 函数创建变换矩阵,通过将变换矩阵指定给父级变换对象的Matrix属性就可以将变换应用于图形对象,实现运动的图形,此处为沿水平直线轨迹运动;沿水平直线轨迹运动动画实现代码如下:
% 运动轨迹
figure
x0 = linspace(-2*pi,2*pi,200);
y0 = zeros(size(x0));
plot(x0,y0)
xlim([-2*pi,2*pi])
axis manual
ax = gca;
h = hgtransform('Parent',ax);
hold on
% 运动的图形
x=linspace(-6*pi,2*pi,400);
y=sin(x);
plot(x,y,'o','Parent',h);
hold off
% 绘制动画
for k = 2:length(x0)
m = makehgtform('translate',x0(k)-x0(1),y0(k)-y0(1),0);
h.Matrix = m;
drawnow
pause(0.01)
end
3.其他二维绘图函数
(1)双y轴图线:plotyy()函数
plotyy(X1,Y1,X2,Y2)
双坐标轴绘图,在同一个坐标轴中画出两个函数的图像,即X1,Y1和X2,Y2。并且[AX,H1,H2] = plotyy(...)是这个函数的返回值,AX是坐标轴句柄,H1和H2分别是两个函数句柄。(通过句柄我们就可以操纵相应的对象)
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
[AX,H1,H2] = plotyy(x,y1,x,y2);
set(get(AX(1),'Ylabel'),'String','Left Y-axis')
set(get(AX(2),'Ylabel'),'String','Right Y-axis')
title('Labeling plotyy');
set(H1,'LineStyle','--'); set(H2,'LineStyle',':');
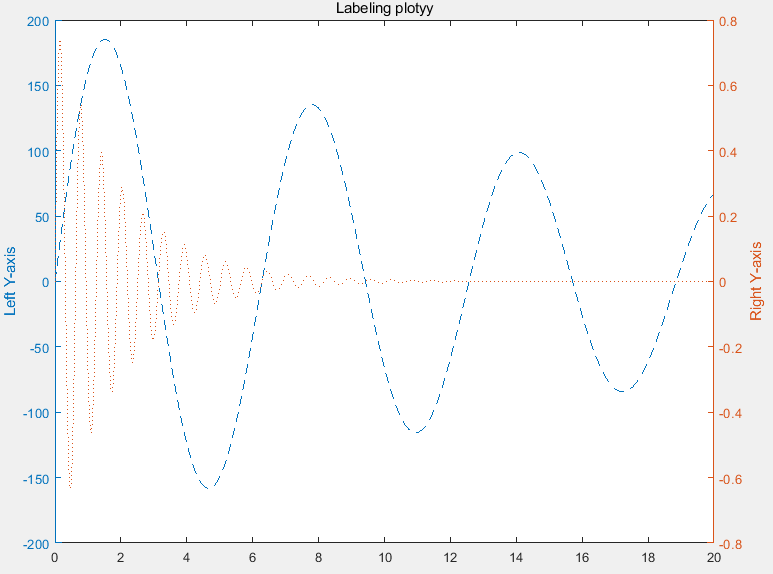

yyaxis()函数的使用:
clear;
clc;
x=0:0.01:20;
y1=200*exp(-0.05*x).*sin(x);
y2=0.8*exp(-0.5*x).*sin(10*x);
yyaxis left %先设置左边Y轴的信息
plot(x,y1,'--');
ylabel('Left Y-axis');
hold on
yyaxis right %设置右边Y轴的信息
plot(x,y2,':r');
ylabel('Right Y-axis');
title('Labeling plotyy');
semilogx()/semilogy()/loglog()
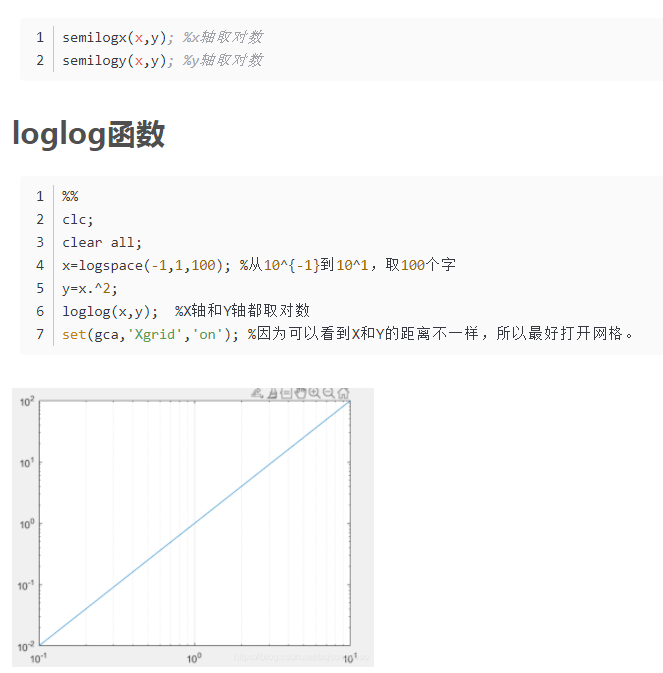
(2)极坐标图线
polar()函数 绘制极坐标或者柱坐标
polar(theta ,r ,lineSpec)
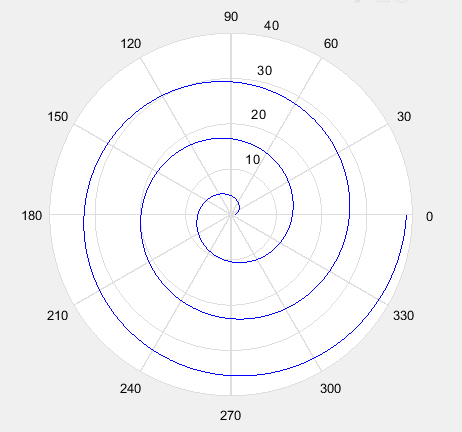
前面说的都是一些常规的直角坐标的图形,我们当然可以在matlab中画出由极坐标或者柱坐标表示的图形。例如著名的阿基米德螺旋线: r = a + b* theta
theta= linspace(0,6*pi,500);
r = 1 + 2*theta;
polar(theta,r,'b-');
theta= linspace(0,2*pi,300);
r = 2 + sin(6*theta);
polar(theta,r,'m-');
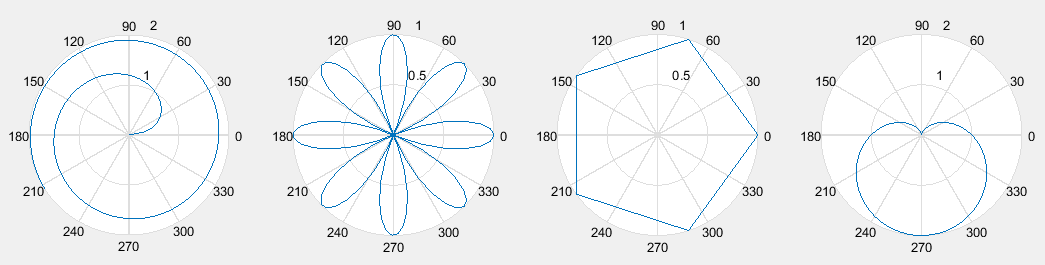
% 螺旋线
x = 1:100; theta = x/10; r = log10(x);
subplot(1,4,1); polar(theta,r);
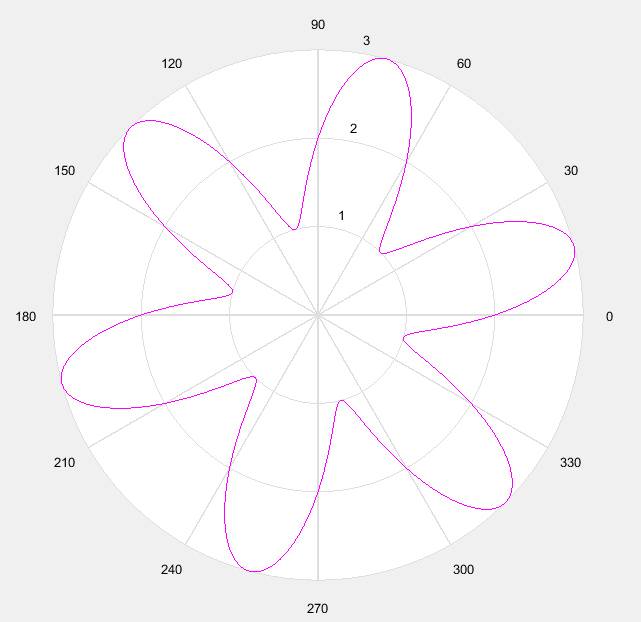
% 花瓣
theta = linspace(0, 2*pi); r = cos(4*theta);
subplot(1,4,2); polar(theta, r);
% 五边形
theta = linspace(0, 2*pi, 6); r = ones(1,length(theta));
subplot(1,4,3); polar(theta,r);
% 心形线
theta = linspace(0, 2*pi); r = 1-sin(theta);
subplot(1,4,4); polar(theta , r);
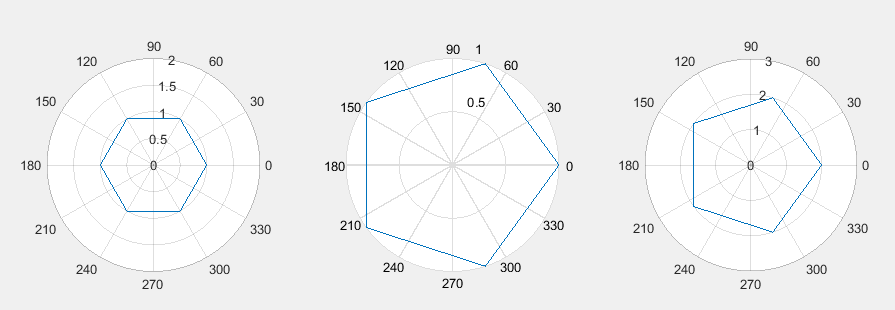
六边形:
clear; 分钟
theta=linspace(0,2*pi,7);
r=ones(1,length(theta));
subplot(1,3,1);polarplot(theta,r);
theta=linspace(0,2*pi,6); r=ones(1,length(theta));
subplot(1,3,2); polar(theta,r);
subplot(1,3,3);
r=[ones(1,length(theta))*2] %将半径变大,则图形也变大
polarplot(theta,r);
(3)fplot()函数
fplot(function, limit,lineSpec)
在我们画图时,很有可能提前不知道函数是怎么样随着自变量变化的,有时候画出来的图形可能达不到我们想要的效果。简单的说,通过fplot()函数中的自适应算法,在画图时,在函数图像密集的地方自变量取值间隔小,在函数图像平坦的地方函自变量取值间隔大,这样就很方便的保证了画图的质量。
其中function如果直接写成函数fplot('x.^2',[2,4]),matlab会提出警告。因此此处应指的是匿名函数即fun = @(arg1,arg2,...) expr,arg是参数,expr可以是一个表达式,也可以是两个表达式,需要用[ ],两个表达式中间用,隔开。例如
f = @(x) [ 2*cos(x)./x , x.^2 ] ;
fplot( f,[-20 , 20] )
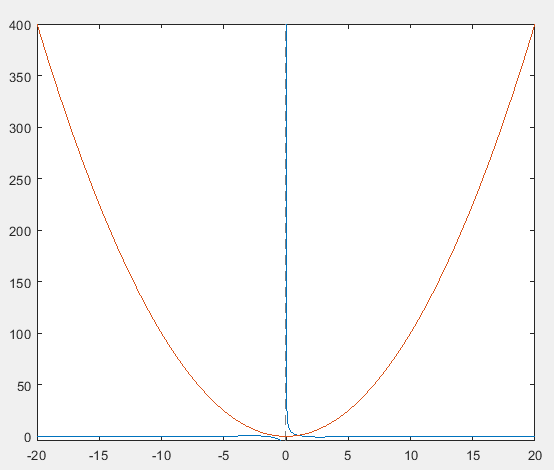
便可以画出在区间2~4上两个函数图像。
limit可以是二维向量[xmin,xmax],也可以是四维向量[xmin,xmax,ymin,ymax]
lineSpec是指定函数的线型,颜色和标记符号。
注意输入的函数必须为单一变量。
(3)ezplot()函数 (主要用于隐函数绘图)
Matlab提供了一个ezplot函数绘制隐函数图形。用法如下:
① 对于函数f=f(x),ezplot的调用格式为:
ezplot(f),在默认区间(-2pi,2pi)绘制图形。
ezplot(f,[a,b]),在区间(a,b)绘制
② 对于隐函数f=f(x,y),ezplot的调用格式为;
ezplot(f),在默认区间(-2pi,2pi),(-2pi,2pi)绘制f(x,y)=0的图形。
ezplot(f,[xmin,xmax,ymin,ymax]);在区间 绘制图形。
ezplot(f,[a,b]),在区间(a,b),(a,b)绘制
③ 对于参数方程x=x(t),y=y(t),ezplot函数的调用格式为:
ezplot(x,y),在默认区间 绘制x=x(t),y=y(t)图形。
ezplot(x,y,[tmin,tmax]),在区间(tmin,tmax)绘制x=x(t),y=y(t)图形。
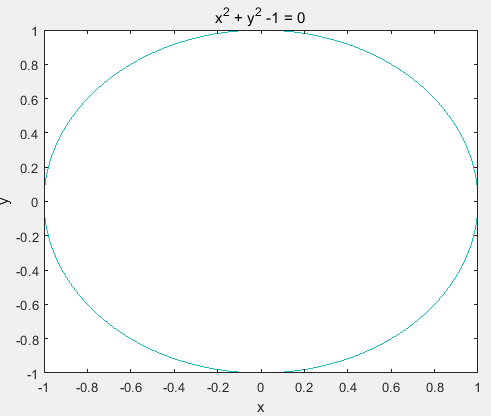
例:
ezplot( ' x^2 + y^2 -1 ' , [-1,1] );
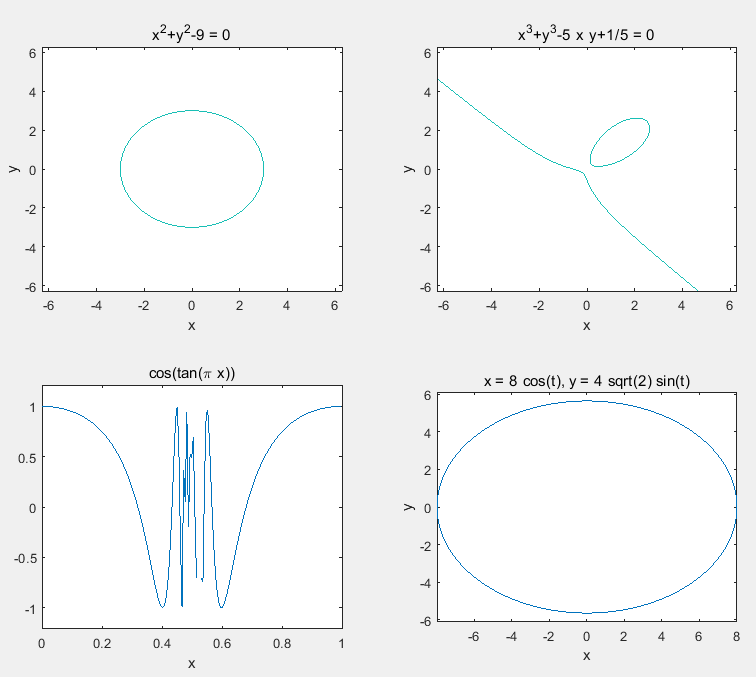
subplot(2,2,1);
ezplot('x^2+y^2-9'); %这里我没有定义自变量范围,系统自动设置
subplot(2,2,2);
ezplot('x^3+y^3-5*x*y+1/5') %系统自动设置自变量范围
subplot(2,2,3);
ezplot('cos(tan(pi*x))',[0,1]); %设定自变量范围0-1
subplot(2,2,4);
ezplot('8*cos(t)','4*sqrt(2)*sin(t)',[0,2*pi]); %设定自变量范围0-2*pi
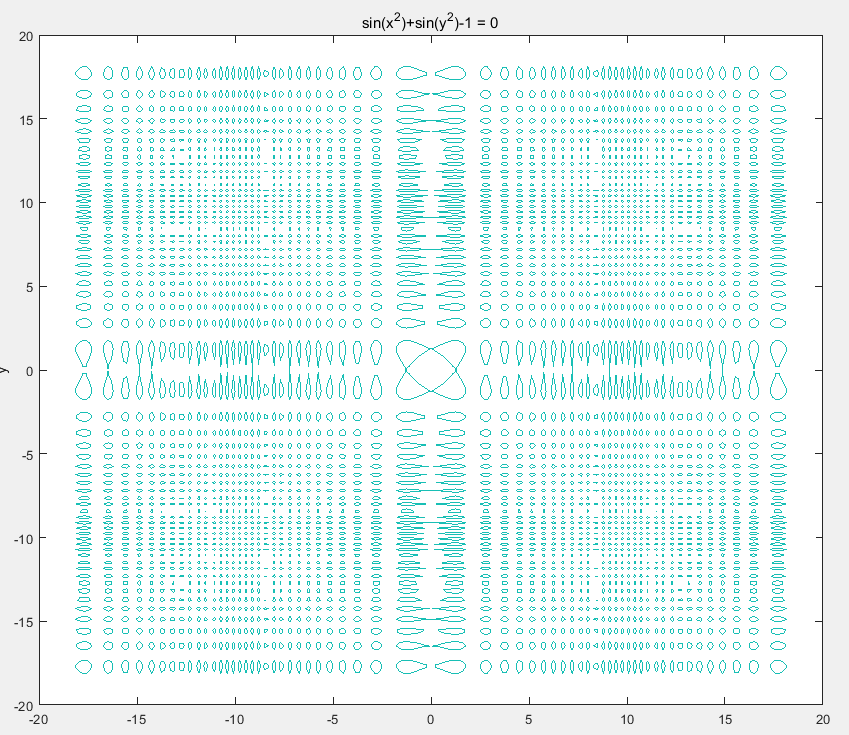
使用ezplot()、ezmesh函数绘制复杂函数图像:sin(x²)+sin(y²)=1
ezplot('sin(x^2)+sin(y^2)-1',[-20,20])
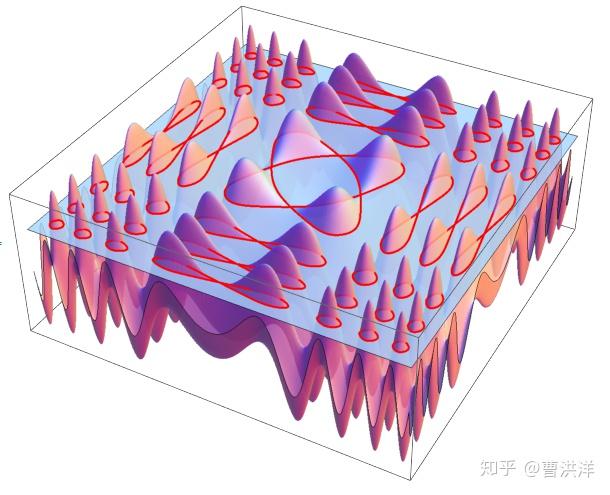
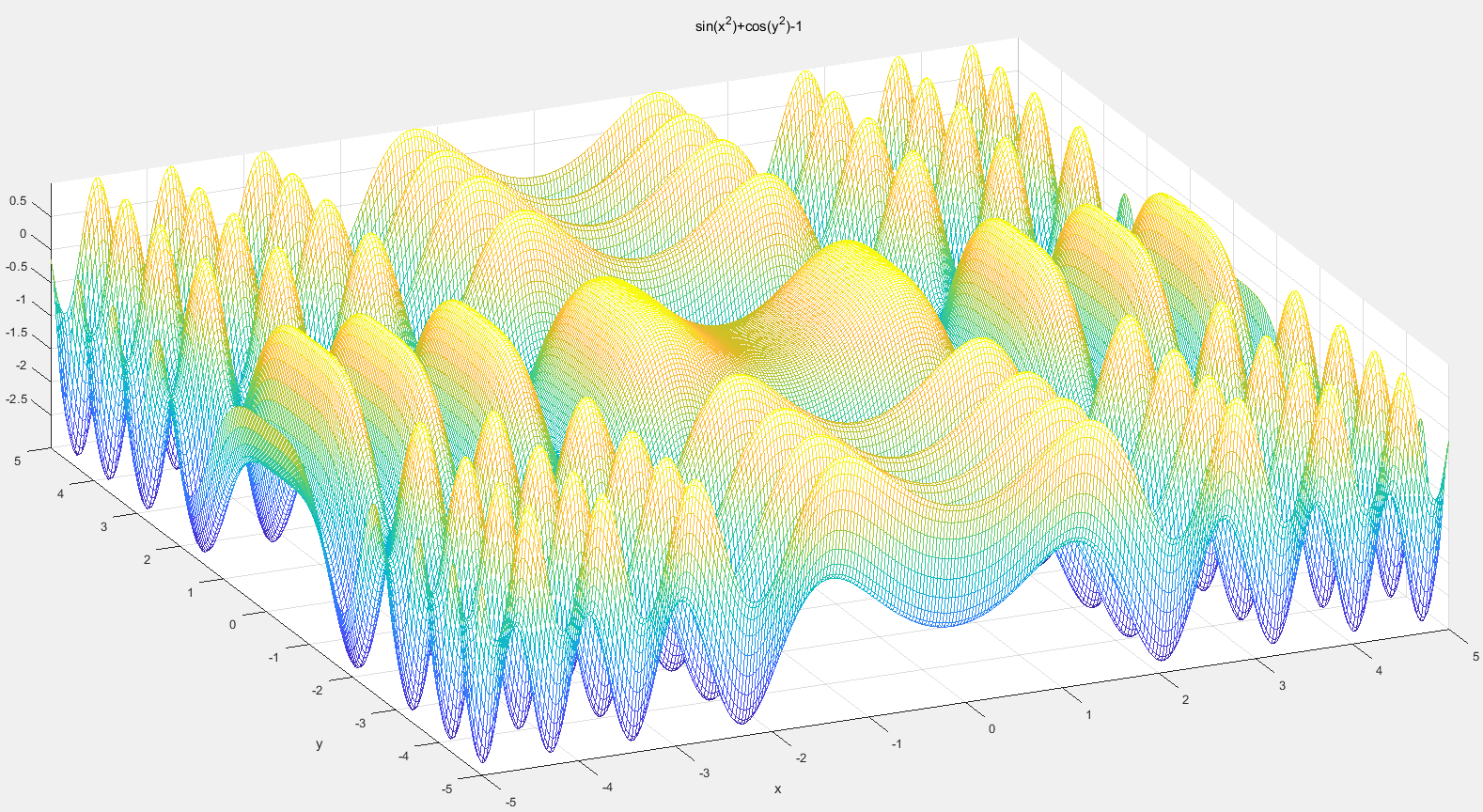
ezmesh('sin(x^2)+cos(y^2)-1',[-5 ,5] ,300)
绘制函数 sin(x²+y²)=cos(x*y)的图像
ezplot('sin(x^2+y^2)-cos(x*y)',[-10,10])
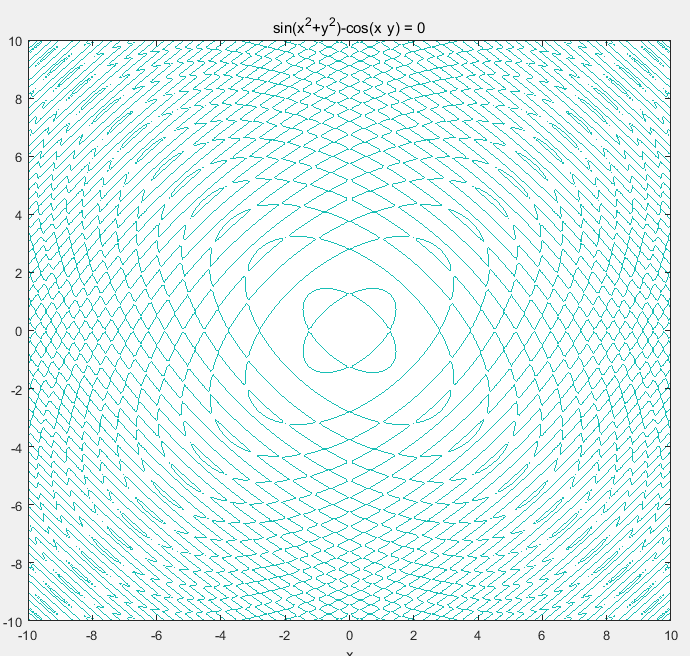
ezmesh('sin(x^2+y^2)-cos(x*y)',[-7,7],500)
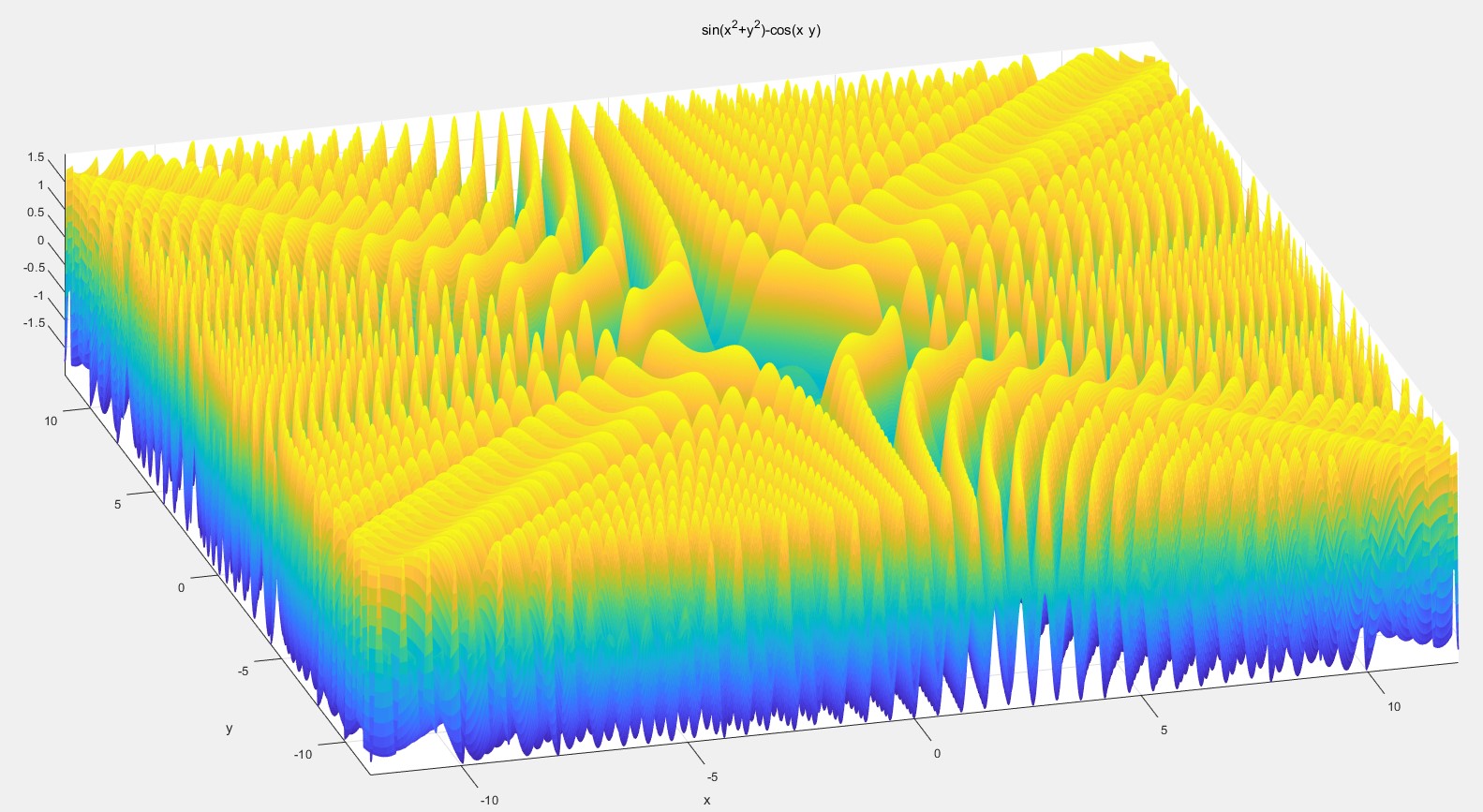
fimplicit(绘制隐函数图像)
说明示例:
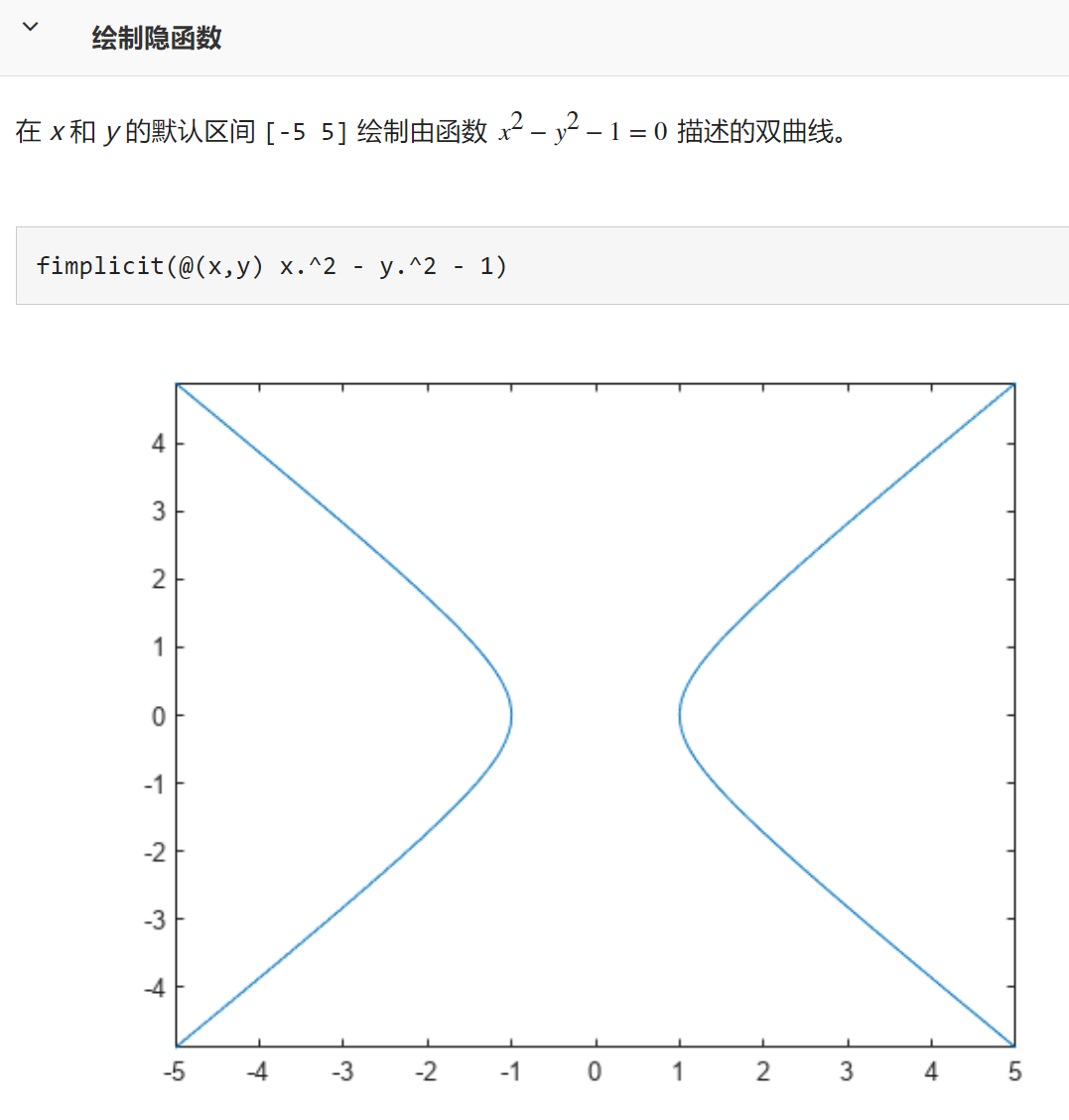
fimplicit(f) 在默认区间 [-5 5](对于 x 和 y)上绘制 f(x,y) = 0 定义的隐函数。
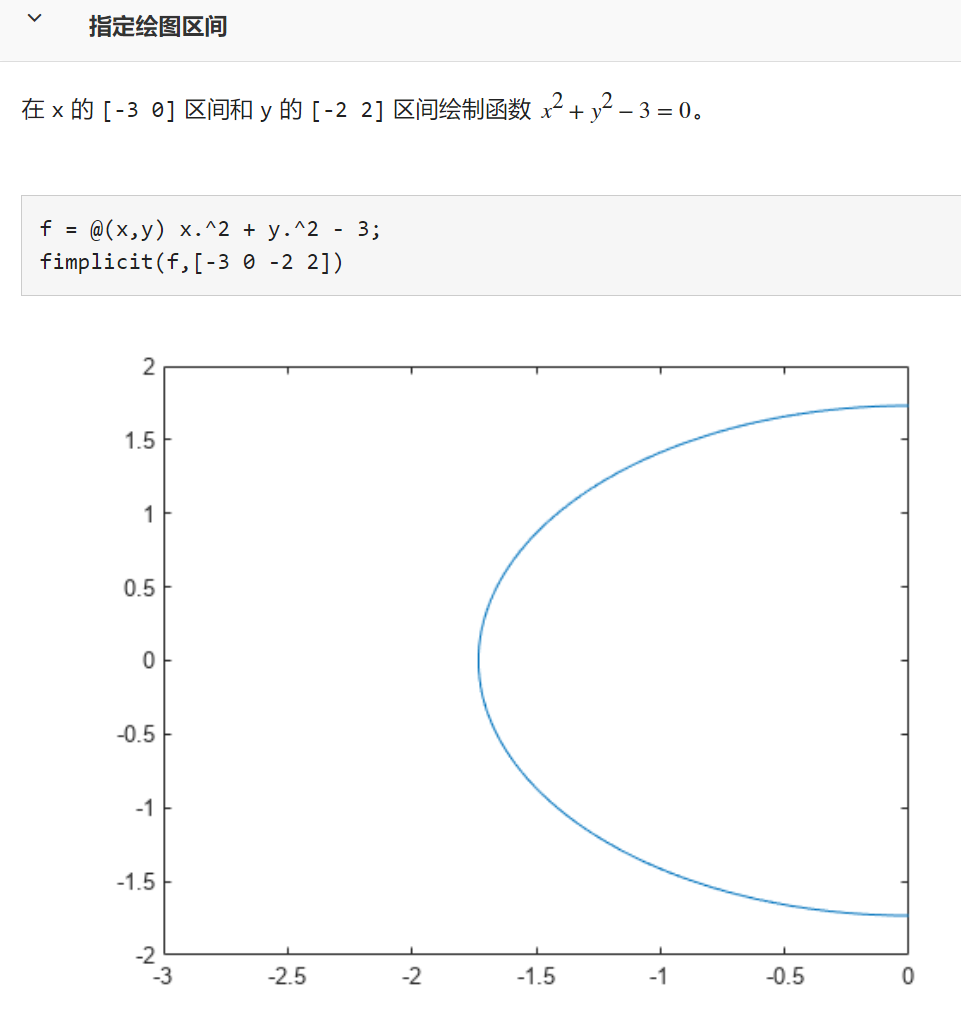
fimplicit(f,interval) 为 x 和 y 指定绘图区间。
fimplicit(ax,___) 将在 ax 指定的坐标区中,而不是在当前坐标区中绘制图形。将坐标区指定为第一个输入参数,先于上述任何输入参数。
fimplicit(___,LineSpec) 指定线型、标记符号和线条颜色。例如,'-r' 绘制一根红色线条。
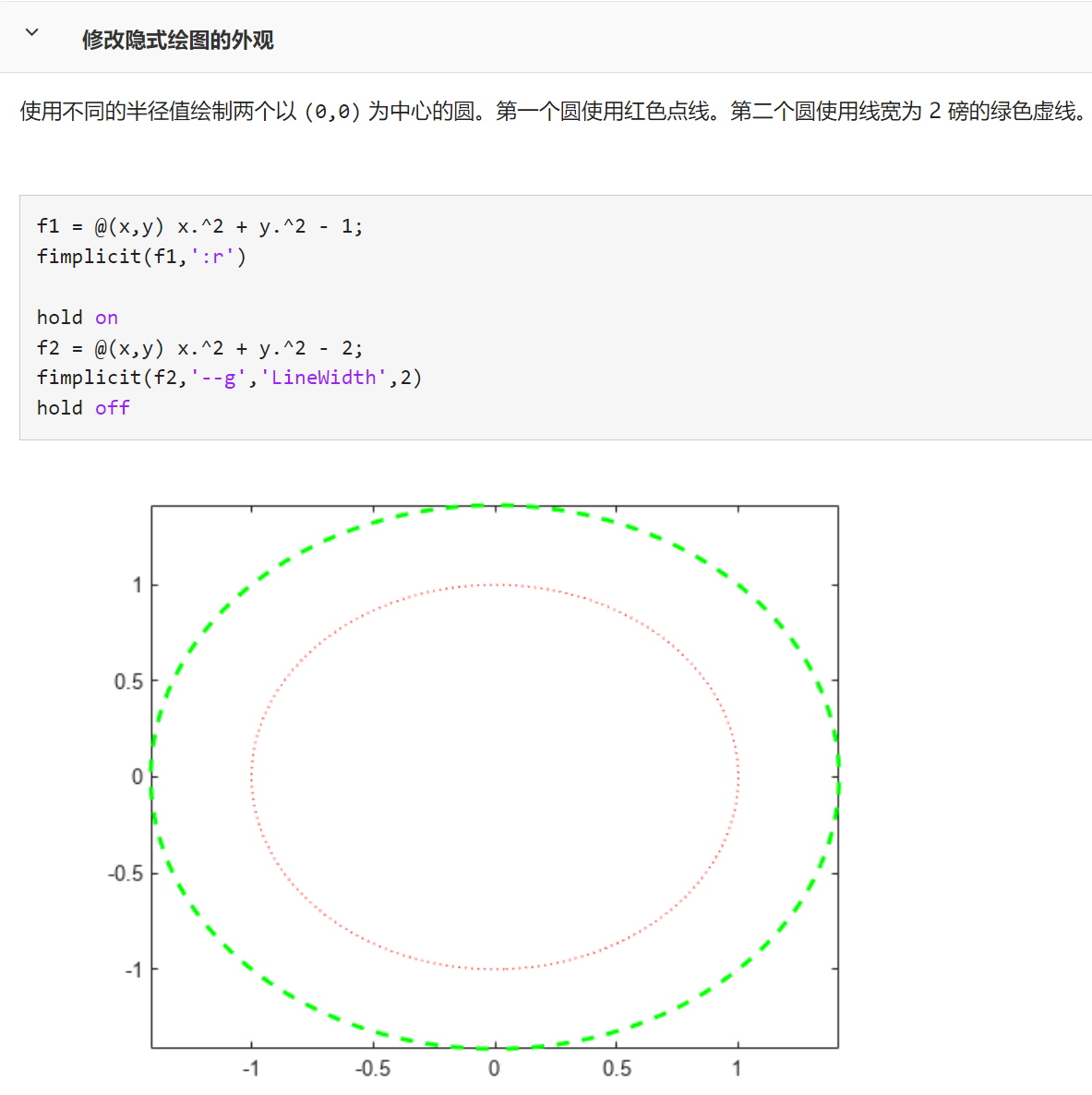
fimplicit(___,Name,Value) 使用一个或多个名称-值对组参数指定线条属性。例如,'LineWidth',2 指定 2 磅的线宽。
fp = fimplicit(___) 返回 ImplicitFunctionLine 对象。使用 fp 可在创建线条后访问和修改线条属性。有关属性列表,请参阅 ImplicitFunctionLine 属性。
close all;clc;
hold on;
fimplicit(@(x,y)(x-2).^2+(y-3+2.*x).^2-5,[1.5,5 -8,3]);
fimplicit(@(x,y)2.*(x-3).^2+(y./3).^2-4,[1.5,5 -8,3]);
hold off;
% 将两个椭圆和求得的交点绘制在同一图形中
fun=@(x)[(x(1)-2).^2+(x(2)-3+2.*x(1)).^2-5,2.*(x(1)-3).^2+(x(2)./3).^2-4];
[x,f,h]=fsolve(fun,[2,2])
[x,f,h]=fsolve(fun,[3.5,-5])
[x,f,h]=fsolve(fun,[4,-4])
hold on;
plot([1.6581 1.7362 3.4829 4.0287],[1.8936 -2.6929 -5.6394 -4.1171],'ro');
fimplicit(@(x,y)(x-2).^2+(y-3+2.*x).^2-5);
fimplicit(@(x,y)2.*(x-3).^2+(y./3).^2-4);
hold off;
-------------------------------------------------------
综合练习:
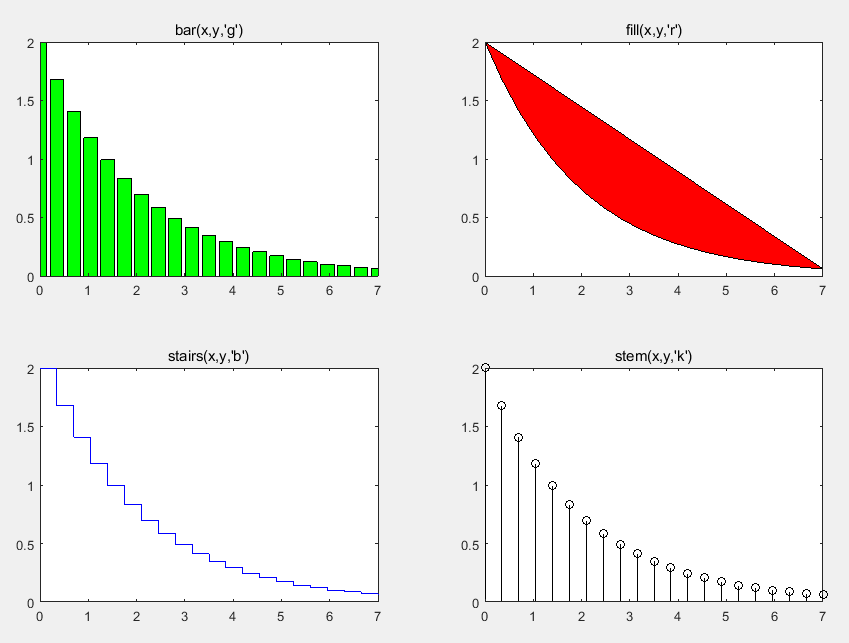
x=0:0.35:7;
y=2*exp(-0.5*x);
subplot(2,2,1); bar(x,y,'g');
title('bar(x,y,''g'')'); axis([0, 7, 0 ,2]);
subplot(2,2,2); fill(x,y,'r');
title('fill(x,y,''r'')'); axis([0, 7, 0 ,2]);
subplot(2,2,3); stairs(x,y,'b');
title('stairs(x,y,''b'')'); axis([0, 7, 0 ,2]);
subplot(2,2,4); stem(x,y,'k');
title('stem(x,y,''k'')'); axis([0, 7, 0 ,2]);
%%上述代码运行后的输出图像如下:
=======================================
实例:花式浪漫爱心(一)
matlab代码:
clear; clc; close all;
% NOTICE: Your MATLAB version should be at least R2019a !
% --------------------------- functions -------------------------------
f = @(x, y, z)(x.^2 + 2.25*y.^2 + z.^2 - 1).^3 - ...
x.^2.* z.^3 - 0.1125*y.^2.*z.^3;
g = @(x, y, z)(sqrt(x.^2+y.^2)-2.5).^2 + z.^2 - 0.4^2;
% -------------------------- generate data ----------------------------
t = linspace(-5, 5);
[x1, y1, z1] = meshgrid(t);
[x2, y2, z2] = meshgrid(t);
val1 = f(x1, y1, z1);
val2 = g(x2, y2, z2);
[p1, v1] = isosurface(x1, y1, z1, val1, 0);
[p2, v2] = isosurface(x2, y2, z2, val2, 0);
% --------------------------- basic plot ------------------------------
figure()
subplot(1, 1, 1)
h = patch('faces',p1,'vertices',v1,'facevertexcdata',jet(size(v1,1)),...
'facecolor','w','edgecolor','flat'); hold on;
patch('faces',p2,'vertices',v2,'facevertexcdata',jet(size(v2,1)),...
'facecolor','w','edgecolor','flat');
grid on; axis equal; axis([-3,3,-3,3,-1.5,1.5]); view(3)
title(["$(x^2+\frac{9}{4}y^2+z^2-1)^3-x^2z^3-\frac{9}{80}y^2z^3=0$",...
"$(\sqrt{x^2+y^2}-R)^2 +z^2 = r^2$"],'Interpreter','latex','position',[3.3,4])
warning('off');
% 请在此处进行您的演讲!% 请在此处进行您的演讲!
T = suptitle("$I\ Love\ U\ !$");
% 请在此处进行您的演讲!% 请在此处进行您的演讲!
set(T,'Interpreter','latex','FontSize',24)
% -------------------------- generate gif -----------------------------
pic_num = 1;
for i = 1:20
v1 = 0.98 * v1;
set(h, 'vertices', v1); drawnow;
F = getframe(gcf);
I = frame2im(F);
[I,map]=rgb2ind(I,256);
if pic_num == 1
imwrite(I,map,'BeatingHeart.gif','gif','Loopcount',inf,'DelayTime',0.05);
else
imwrite(I,map,'BeatingHeart.gif','gif','WriteMode','append','DelayTime',0.05);
end
pic_num = pic_num + 1;
end
for i = 1:20
v1 = v1 / 0.98;
set(h, 'vertices', v1); drawnow;
F = getframe(gcf);
I = frame2im(F);
[I,map] = rgb2ind(I,256);
imwrite(I,map,'BeatingHeart.gif','gif','WriteMode','append','DelayTime',0.05);
pic_num = pic_num + 1;
end
% ----------------------------- dynamic -------------------------------
while true
for i = 1:20
v1 = 0.98 * v1;
set(h, 'vertices', v1); drawnow;
end
for i = 1:20
v1 = v1 / 0.98;
set(h, 'vertices', v1); drawnow;
end
end
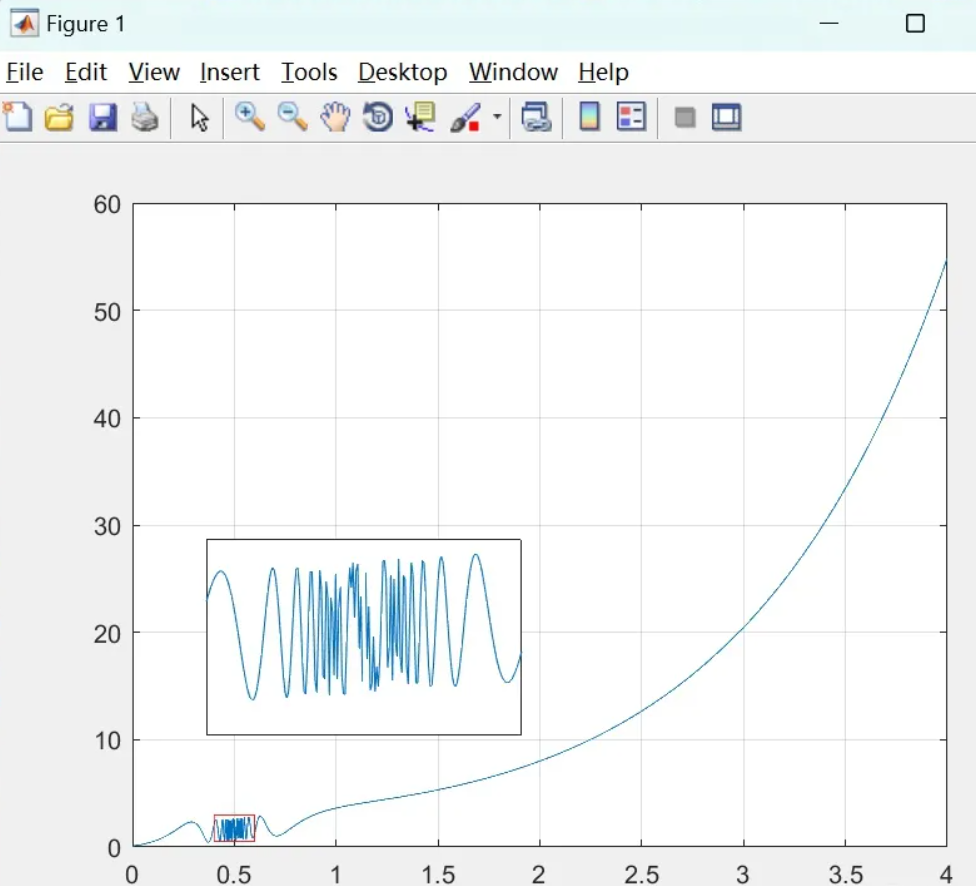
Matlab怎么画局部放大图?
x = 0:0.001:4; % total x-axis
y = exp(x)+sin(1./(x-0.5));
% sub region to enlarge
x1 = 0.4:0.0001:0.6;
y1 = exp(x1)+sin(1./(x1-0.5));
% main figure
figure;
plot(x, y);
grid on;
rectangle('Position', [min(x1) 0.5 max(x1)-min(x1) 2.5], 'EdgeColor', 'r'); % mark the region to enlarge
% sub figure
sub = axes('Position', [0.20, 0.25, 0.30, 0.25]); % location of the sub figure
plot(x1, y1);
xlim([min(x1), max(x1)]);
set(sub, 'xtick', [], 'ytick', []);
========================================
========================================
作业1:
根据绘图知识点的学习,自己设计6个数学函数,然后以2行3列的
方式把6个函数图像以子图的方式输出,并尽量装饰图像(比如,设计图像的
线条颜色,线型,线宽等,增加xlabel,title, grid on,axis等控制命令等)。
并要使用以下绘图命令:plot,fplot,ezplot,ezmesh,polar,area(x,y) ,
stem(x,y) , stairs(x,y)等绘图命令
作业2:采用ezmesh和ezplot分别画出下面两个函数的三维和二维图像。
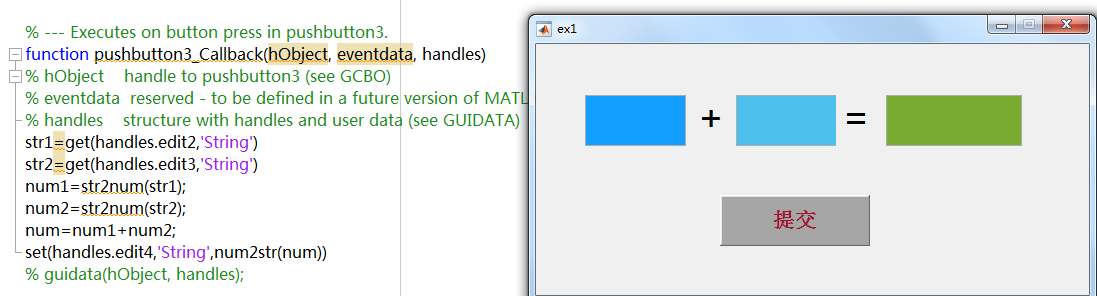
3.采用GUIDE的方式设计一个加法器 (1)界面的要求: 包括3个动态文本窗口(其中2个用于接收输入数字,1个用于显示加法结果), 2个静态文本窗口(一个“+”号,一个‘=’号),1个按钮。然后通过双击各个控件, 来更改控件的属性(如文字大小,颜色,背景颜色等);并先保存文件。 (2)设置按钮(pushbutton)的回调函数,过程为:用get()函数接收动态文本 窗口edit1和edit2的‘string’属性的内容(既,输入的数字),然后把接收的 数字从字符状态,转换为数值状态;然后把两个数值相加,再把相加的和转换为字符 状态,再通过set()函数,设置edit3的string’属性的内容(既,把数字的和,赋值给 ‘string’属性); (3)保存gui,然后运行测试。效果类似如下:
(4)如果有学有余力,可以试着做一个减法,乘法,等计算器。