作业3:求任意给定的一个五位正整数的个位、十位、百位，千位、万位。
效果如下：
要求应用两种方法。
课程作业与答案
上一节
下一节
第一章作业
1.5
作业1：
创建一个计算三角形面积的脚本文件。运行此脚本时，用input函数要求对方输入三角形的三个边长，然后输出三角形面积。
clear
a = input ('请输入三角形第1个边长 a = ');
b = input ('请输入三角形第2个边长 b = ');
c = input ('请输入三角形第3个边长 c = ');
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
fprintf('输入的三角形面积为：%.3f \n',s)
1.7
作业1：编程实现把任何一个输入的2*2的矩阵a变成10*10的矩阵y
要求效果如下：
、
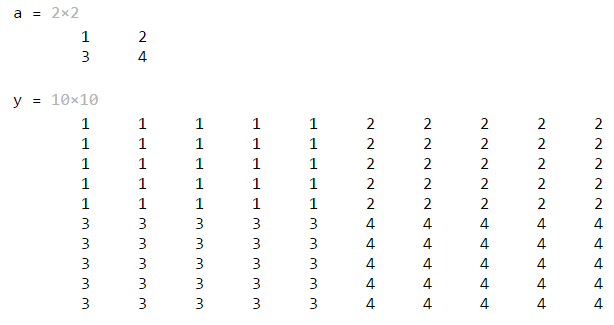提示，有两种方法。
方法1采用repmat函数；
方法2采用如下索引方式
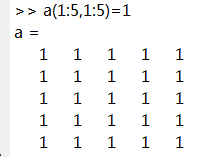
% 方法1采用repmat函数；
clear
a=[1,2;3,4]
y=zeros(10) %初始化y，占一个10*10的位置先
y(1:5,1:5)=repmat(a(1,1),5,5);
y(1:5,6:10)=repmat(a(1,2),5,5);
y(6:10,1:5)=repmat(a(2,1),5,5);
y(6:10,6:10)=repmat(a(2,2),5,5);
y
% 方法2采用如下索引方式
clear
a=[1,2;3,4]
y=ones(10)
y(1:5,1:5)=a(1,1);
y(1:5,6:10)=a(1,2);
y(6:10,1:5)=a(2,1);
y(6:10,6:10)=a(2,2);
y
作业2：
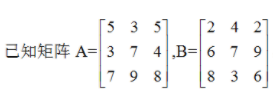
（1）先把A和B按纵向合成为一个6*3的矩阵C，然后再把C的3个列向量串接成一个18*1的列向量D，然后把D再变为一个1*18的行向量E。
（2）把上一步得到的行向量E，采用reshape函数变形为一个2*9的新矩阵F；
（3）采用cat（）函数把A和B合并成一个3*3*2的三维数组G。
clear
A=[5 3 5;3 7 4;7 9 8]
B=[2 4 2;6 7 9;8 3 6]
C=[A;B]
D=C(:)
E=D'
F=reshape(E,2,9)
G=cat(3,A,B)
作业3：（1）创建一个5*10*3的随机整数三维数组，要求所有元素都是1-150之间的整数，且不许重复（提示：使用randperm函数）；（2）先求每一面中的最大值和最小值，再求整个矩阵的最大值和最小值；
clear
x=randperm(150)
y=reshape(x,5,10,3)
y1_max=max(y(:,:,1),[],'all')
y2_max=max(y(:,:,2),[],'all')
y3_max=max(y(:,:,3),[],'all')
y1_min=min( min(y(:,:,1)) )
y2_min=min( min(y(:,:,2)) )
y3_min=min( min(y(:,:,3)) )
y_max=max(y(:))
y_min=min(y(:))
%以上采用三种方法求最值，细心体会
作业4：（1）创建5*10的符合正态分布（均值为0）的随机矩阵a。（2）分别对a矩阵的行方向进行升序排序得到矩阵B，再对B矩阵的列方向降序排序得到矩阵C。（3）求这个C矩阵所有元素之和，以及元素的平均值。
clear
a=randn(5,10)
B=sort(a,2)
c=sort(B,1,'descend')
c_sum=sum(c(:))
c_mean=c_sum/numel(c) %或者 c_mean=mean(c(:))
作业5：（1）创建5*5的魔方矩阵；（2）对这个矩阵先进行顺时针90°的旋转，再上下翻转；（3）验证得到的这个新矩阵的，各行之和，各列之和，左对角线之和（提示：需要把对角线元素一个个都索引出来，作为一个行向量，再来求和），右对角线之和，看看这些和是否相等？
%参考答案
m0=magic(5)
m1=rot90(m0,-1)
m2=flipud(m1)
dig_l=diag(m2)
dig_r=diag( rot90(m2) )
sum(m2,1)
sum(m2,2)
sum(dig_l)
sum(dig_r)
m0 =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
m1 =
11 10 4 23 17
18 12 6 5 24
25 19 13 7 1
2 21 20 14 8
9 3 22 16 15
m2 =
9 3 22 16 15
2 21 20 14 8
25 19 13 7 1
18 12 6 5 24
11 10 4 23 17
dig_l =
9
21
13
5
17
dig_r =
15
14
13
12
11
ans =
65 65 65 65 65
ans =
65
65
65
65
65
ans =
65
ans =
65
作业6：生成一个400*400像素的纯色图（颜色调节到自己喜欢的状态）。提示，采用ones()/cat() 等函数生成400*400*3的三维数组，作为RGB三个通道的数据，然后用imshow()函数显示这个数组。
clear
kr=0.78;
kg=0.11;
kb=0.39;
r=ones(400)*kr;
g=ones(400)*kg;
b=ones(400)*kb;
pic=cat(3,r,g,b);
imshow(pic)
1.8
作业1：
（1）创建一个5行4列的元胞数组，要求：第一行是4个字符串，依次为：'姓名'，'籍贯'，'学号'，'电话'；第2-5行分别是4个具体同学的实例。
（2）创建好之后，显示输出（celldisp）该元胞数组内容，并画出(cellplot)其结构。
（3）分别对具体某个学生的姓名或者学号、电话等，进行索引。
作业2：
创建一个4行5列的元胞数组，此元胞数组中的每一个单元都是一个字符串（假设为网站中用户注册时分配的初始用户名），此字符串长度为6，这6个字母是从62个字符（26个字母的大小写，加上10个数字字符）中随机选择的。
提示：
>> x='a':1:'z'
x =
'abcdefghijklmnopqrstuvwxyz'
>> x( [randi(26,1,3)] )
ans =
'vxd'
或：
x='a':1:'z'
y=x( [randperm(26)] )
y(1:3)
x =
'abcdefghijklmnopqrstuvwxyz'
y =
'mnideoywjbukzacsthrpxqvlfg'
ans =
'mni'
练习1：对随机矩阵a=randn(10,10),如何计算矩阵a中处于-1到+1之间的元素总数目？
%
%方法1
a=randn(10,10)
y=(a>-1)&(a<1)
z=a(y)
numel(z)
%方法2
y=(a>-1)&(a<1)
sum(y(:))
练习2: 模拟50个同学某门课的期末成绩（随机分布在30-100之间），找出不及格的人数，以及占班级总人数的百分比。再把50-59分的分数置为60。
n=50
s=randi([30,100],1,n)
y=s<60
z=sum(y)
z/n
y2=(s>=50)&(s<=59)
s(y2)=60
1.10
作业1：（1）采用随机函数randn()生成一个10*10的随机矩阵A，假设x为A中的任意一个元素，采用逻辑索引等方法找出A中所有满足：-1<x<-0.5，以及0.5<x<1的元素，把这些元素给y。
（2）求出，数组y的元数的总数。
（3）把A中满足（1）中要求的元素替换成0；
作业2：利用蒙特卡洛法计算圆周率
步骤：
（1）先用rand函数生成方形区域内的n个点的所有横坐标组成的数组x（1*n的数组），再生成这n个点的纵坐标组成的数组y（1*n的数组）；并用plot(x,y,'*')画出这n个点的图像；
（2）计算所有的n个点和圆心的距离r（r也是一个1*n的数组）；
（3）判断每个点的r与设定的圆的半径r0=1的大小逻辑关系，计算位于圆内的点数m。
（4）利用公式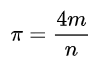
，计算pi的值。
提示：如何确定数组x=rand(1,20)中大于0.8的元素的个数,以及所有大于0.8的元素之和？
x=rand(1,20)
y=(x>0.8) %大小关系的逻辑判断，得到一个1*20的逻辑数组
y_num=sum(y) %求这个逻辑数组的和（所有1的和`），既为符号要求的点数
z=x(y) %使用逻辑数组y索引出x中符合要求的元素，给z
z_num=sum(z) %算出z中所有元素之和
作业3.设x=randi(10,3,10); y=randi([5,20],5,10);求x与y的交集、并集，并用unique（）函数对x和y进行瘦身。
1.11
作业1：通过学习本节的知识，编程生成一个4*4网格的随机彩色图，既共16个单元格（每个单元格子大小为100*100像素）。每次运行代码，都能得到不同颜色分布的随机图案。
参考：3*3时的情况
方法1：
%膨胀法（把小图的每个像素点膨胀后填充到大图的对应区域内）
clear all
k=3; %设置网格为k*k
n=100; %设置膨胀倍数n
rgb1=rand(k,k,3); %原始的k*k像素的3通道小彩图
imshow(rgb1)
%下面开始膨胀操作。
rgb=zeros( k*n , k*n , 3 ); %初始化rgb三维数组，初始值都设为0
rgb(1:100,1:100,:) =repmat(rgb1(1,1,:),100,100) ;
rgb(1:100,101:200,:)=repmat(rgb1(1,2,:),100,100) ;
rgb(1:100,201:300,:)=repmat(rgb1(1,3,:),100,100);
rgb(101:200,1:100,:) =repmat(rgb1(2,1,:),100,100);
rgb(101:200,101:200,:)=repmat(rgb1(2,2,:),100,100);
rgb(101:200,201:300,:)=repmat(rgb1(2,3,:),100,100);
rgb(201:300,1:100,:) =repmat(rgb1(3,1,:),100,100);
rgb(201:300,101:200,:)=repmat(rgb1(3,2,:),100,100);
rgb(201:300,201:300,:)=repmat(rgb1(3,3,:),100,100);
imshow(rgb)
方法2：
组合法（先生成9个100*100的随机纯色块，然后拼接成一个3*3的九宫格）
clear all
n=100; %设置每个基础色块的像素值
o=ones( n , n , 3 ); %初始化rgb三维数组，初始值都设为0
rgb11=o.*rand(1,1,3); %对每个色块随机染色。
rgb12=o.*rand(1,1,3);
rgb13=o.*rand(1,1,3);
rgb21=o.*rand(1,1,3);
rgb22=o.*rand(1,1,3);
rgb23=o.*rand(1,1,3);
rgb31=o.*rand(1,1,3);
rgb32=o.*rand(1,1,3);
rgb33=o.*rand(1,1,3);
rgb=[rgb11,rgb12,rgb13;rgb21,rgb22,rgb23;rgb31,rgb32,rgb33];
imshow(rgb)
答案：
clear all
n=100; %设置每个基础色块的像素值
o=ones( n , n , 3 ); %初始化rgb三维数组，初始值都设为0
rgb11=o.*rand(1,1,3); %对每个色块随机染色。
rgb12=o.*rand(1,1,3);
rgb13=o.*rand(1,1,3);
rgb14=o.*rand(1,1,3);
rgb21=o.*rand(1,1,3);
rgb22=o.*rand(1,1,3);
rgb23=o.*rand(1,1,3);
rgb24=o.*rand(1,1,3);
rgb31=o.*rand(1,1,3);
rgb32=o.*rand(1,1,3);
rgb33=o.*rand(1,1,3);
rgb34=o.*rand(1,1,3);
rgb41=o.*rand(1,1,3);
rgb42=o.*rand(1,1,3);
rgb43=o.*rand(1,1,3);
rgb44=o.*rand(1,1,3);
rgb=[rgb11,rgb12,rgb13,rgb14;
rgb21,rgb22,rgb23,rgb24;
rgb31,rgb32,rgb33,rgb34;
rgb41,rgb42,rgb43,rgb44];
imshow(rgb)
作业2：（1）采用randi([1,300],[10,15])生成一个10*10的随机整数矩阵A；（2）采用逻辑索引的方法，索引出矩阵A中所有可以被3整除的元素；（3）并计算出上一步索引出的元素的总数；(4)找出A中所有不能被3整除也不能被7整除的元素的总数；（5）把A中所有可以被3整除的元素替换成0。
答案：
%（1）采用randi([1,300],[10,10])生成一个10*10的随机整数矩阵A；
clear
A=randi([1,300],[10,10])
%（2）采用逻辑索引的方法，索引出矩阵A中所有可以被3整除的元素；
y1= (mod(A,3)==0)
z=A(y1)
%（3）并计算出上一步索引出的元素的总数；
numel(z)
% (4)找出A中所有不能被3整除也不能被7整除的元素的总数；
y2=(mod(A,3)~=0)&(mod(A,7)~=0)
sum(y2(:))
%（5）把A中所有可以被3整除的元素替换成0。
A(y1)=0
方法1，采用num2str函数以及字符数组的方法。
方法2，采用fix（）等函数方法。
% 方法1：采用num2str函数以及字符数组的方法。
x=32487;
y=num2str(x)
fprintf('个位数为%s, 十位数为%s, 百位数为%s, 千位数为%s, 万位数为%s,\n',y(5),y(4),y(3),y(2),y(1))
% 方法2：采用fix（）等函数方法。
x=32487
y1=fix(x/10000);
y2=fix(x/1000)-y1*10; %y2=mod(fix(x/1000),10)
y3=fix(x/100)-y1*100-y2*10;
y4=fix(x/10)-y1*1000-y2*100-y3*10;
y5=x-y1*10000-y2*1000-y3*100-y4*10;
fprintf('个位数为%d, 十位数为%d, 百位数为%d, 千位数为%d, 万位数为%d, \n',y5,y4,y3,y2,y1)
% 方法3：采用fix/mod等函数方法。
x=32487
y1=mod(x,10)
y2=mod(fix(x/10),10)
y3=mod(fix(x/100),10)
y4=mod(fix(x/1000),10)
y5=mod(fix(x/10000),10)
fprintf('个位数为%d, 十位数为%d, 百位数为%d, 千位数为%d, 万位数为%d, \n',y1,y2,y3,y4,y5)
作业4:(1)利用randn()函数生成一个5*10的矩阵A，用ceil处理A得到矩阵x，用 floor处理A得到矩阵y，用round处理A得到矩阵z，用fix处理A得到矩阵t;
(2)计算x+y-(z+t);
A=randn(5,10)
x=ceil(A)
y=floor(A)
z=round(A)
t=fix(A)
x+y-(z+t)
第二章作业
作业1.邮件地址切片器
目的：编写一个脚本，可以从用户给出的邮箱地址中获取用户名和域名。
如果用户输入的邮箱不符合规则，则输出：邮箱格式有误。如果邮箱格式正确，则给出用户名和域名。
效果如下：
（1）如果输入的邮箱（需要单引号引住）格式有误，即：帐号+@+域名，这三者缺少一个，则输出“邮箱格式有误！
（2）如果邮箱格式正确，则输出邮箱的账号和域名。
提示：邮箱地址一般是帐号@域名的格式，就是帐号+@+域名，这三个部分组成。可以使用@作为分隔符，将地址分为分为两个字符串。如果这三个部分，缺少任何一部分，则认为邮箱格式有误。可以使用strfind()等函数，加上if判断,,以及判断数组是否为空的函数isempty( )等.
clear
s=input('请输入你的邮箱(email) :')
L= ? %得到字符串s的长度
num_at= ? %判断输入的字符串里面的“@”的数量num_at，是否超过了2个
if ? %如果“@”超过2个，或者等于0个，或者“@”在开头，或者“@”在末尾
fprintf('邮箱格式有误！\n' );
else
s1= ? %把账号部分切片出来给s1
s2= ? %把域名部分切片出来给s2
fprintf('帐号为%s,域名为%s \n',s1,s2);
end
答案：
%方法1
clear
s=input('请输入你的邮箱(email) :')
L= length(s) %得到字符串s的长度
num_at= sum( s=='@') %判断输入的字符串里面的“@”的数量num_at
if num_at>=2|num_at==0|s(1)=='@'|s(end)=='@'
%如果“@”超过2个，或者等于0个，或者“@”在开头，或者“@”在末尾
fprintf('邮箱格式有误！\n' );
else
k=strfind(s,'@');
s1=s(1:k-1);
s2=s(k+1:L);
fprintf('帐号为%s,域名为%s \n',s1,s2);
end
%方法2
clear
s=input('请输入你的邮箱(email) :')
L=length(s);
k=strfind(s,'@');
num_at=length(k); %判断输入的字符串里面的“@”是否超过了2个
if isempty(k)|k==1|k==L|num_at>=2
fprintf('邮箱格式有误！\n' );
else
s1=s(1:k-1);
s2=s(k+1:L);
fprintf('帐号为%s,域名为%s \n',s1,s2);
end
2.3
作业：
设定一个分数标准： 0-59：E级 60-69：D级 70—79：C级 80—89：B级 90-100：A级； 按照这个分数标准对输入的成绩进行等级评判（即，输出这个分数对对应的等级）。
（1）用if语句实现
（2）用switch语句实现
答案：
%用if语句实现
clear
score=37
if score>=90&score<=100
fprintf('成绩为A级 \n');
elseif score>=80&score<89
fprintf('成绩为B级 \n');
elseif score>=70&score<79
fprintf('成绩为C级 \n');
elseif score>=60&score<69
fprintf('成绩为D级 \n');
else
fprintf('成绩为E级 \n');
end
%用switch语句实现，方式1
clear
score=97
k=fix(score/10)
switch k
case {9,10}
fprintf('成绩为A级 \n');
case {8}
fprintf('成绩为B级 \n');
case {7}
fprintf('成绩为C级 \n');
case {6}
fprintf('成绩为D级 \n');
otherwise % 或者写成 case {0 1 2 3 4 5}
fprintf('成绩为E级 \n');
end
%用switch语句实现，方式2
clear
score=97
switch score
case num2cell(90:100)
fprintf('成绩为A级 \n');
case num2cell(80:89)
fprintf('成绩为B级 \n');
case num2cell(70:79)
fprintf('成绩为C级 \n');
case num2cell(60:69)
fprintf('成绩为D级 \n');
otherwise % 或者写成 case num2cell(0:59)
fprintf('成绩为E级 \n');
end
2.4
作业1：制作一个成绩计算程序。
（1）第1步，用input函数，让对方依次输入任意两个0-100之间的数，分别赋给变量X_ps和 X_qm。 其中变量X_ps, X_qm分别表示平时分和期末卷面分，S_zf表示总分。要求判断输入的X_ps和 X_qm是否在0-100之间，如果不在，则输出警告，并要求对方重新输入正确的数值.....直到满足两个数都在0-100之间。
（2）第2步，根据上一步得到的平时分和期末分，计算总分S_zf，公式如下：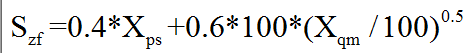
（3）第3步，采用if或者 switch语句执行以下动作：
当总分S_zf在90-100这个区间时，输出：您的平时分为：*** 卷面分为:*** 总分为：*** 成绩优秀。
当总分S_zf在70-89.9这个区间时，输出：您的平时分为：*** 卷面分为:*** 总分为：*** 成绩良好。
当总分S_zf在60-69.9这个区间时，输出：您的平时分为：*** 卷面分为:*** 总分为：*** 成绩及格。
当总分S_zf在0-59.9这个区间时，输出： 您的平时分为：*** 卷面分为:*** 总分为：*** 等着补考吧。
（提示：需要用到while循环、 if或者 switch分支，fprintf格式输出，数值的大于、小于、与或非等逻辑判断语句。）
clear
while 1
X_ps=input('请输入你的平时分：');
X_qm=input('请输入你的期末考试分：');
if X_ps>100 | X_ps<0 | X_qm>100 | X_qm<0
fprintf('输入有误，输入的分数应该在0-100之间.请重新输入 \n')
else
break
end
end
S_zf=0.4*X_ps+0.6*100*(X_qm/100)^0.5;
if S_zf>=90
fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 成绩优秀. \n' ,X_ps,X_qm, S_zf);
elseif S_zf>=70&S_zf<90
fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 成绩良好. \n',X_ps,X_qm, S_zf);
elseif S_zf>=60&S_zf<70
fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 成绩及格. \n',X_ps,X_qm, S_zf);
elseif S_zf<60
fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 等着补考吧. \n',X_ps,X_qm, S_zf);
end
%方法2：采用switch模式
% switch fix(S_zf/10)
% case {9,10}
% fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 成绩优秀. \n' ,X_ps,X_qm, S_zf);
% case {7,8}
% fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 成绩良好. \n',X_ps,X_qm, S_zf);
% case {6}
% fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 成绩及格. \n',X_ps,X_qm, S_zf);
% otherwise
% fprintf('您的平时分为：%5.2f 卷面分为:%5.2f 总分为：%5.2f 等着补考吧. \n',X_ps,X_qm, S_zf);
% end
作业2：计算三角形面积
创建一个计算三角形面积的脚本文件。运行此脚本时，用input函数要求对方输入三角形的三个边长，然后输出三角形面积。要求判断输入的三个边长是否满足三角形的基本要求（三角形总是满足任意两边和大于第三边），不满足则要求重新输入。
clear
while 1
a = input ('请输入三角形第1个边长 a = ');
b = input ('请输入三角形第2个边长 b = ');
c = input ('请输入三角形第3个边长 c = ');
if (a+b)>c&(a+c)>b&(b+c)>a
fprintf('这是一个合理的三角形\n')
break
else
fprintf('输入的三个边长构不成三角形，请重新输入 \n')
end
end
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
fprintf('输入的三角形周长为：%.3f ， 面积为：%.3f \n',a+b+c,s)
作业3：对数组x=randi([1,99],5,20),按行查找，把每一行第一个能被7整除的数找出来，输出该数，然后停止查找该行，进入下一行继续查找。
提示：需要用到双重的嵌套(while或for)循环，以及break语句等。。
%方法1：
clear
x=randi([1,99],5,20)
[row,col]=size(x)
taget=7;
for n=1:row
for m=1:col
if mod(x(n,m),taget)==0
fprintf('在第%d行的第%d列，找到首个能被%d整除的数，这个数是%d \n',n,m,taget,x(n,m))
break
end
end
end
%方法2：
clear
x=randi([1,99],5,20)
[row,col]=size(x)
taget=7;
n=1;
m=1;
while n<=row
while m<=col
if rem(x(n,m),taget)==0
fprintf('In row %d ,col %d ,find the number your wanted is %d \n',n,m,x(n,m))
break
end
m=m+1;
end
m=1;
n=n+1;
end
%方法3：
clear
x=randi([1,99],5,20)
[row,col]=size(x)
taget=7;
n=1;
m=1;
while n<=row
if rem(x(n,m),taget)==0
fprintf('In row %d ,col %d ,find the number your wanted is %d \n',n,m,x(n,m))
n=n+1;
m=1;
continue
end
m=m+1;
end
作业4：用while循环求解e的值。
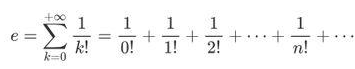
任务1：编程计算e的值，要求当最后一项的值1/n!<0.000001时结束计算，并输出此时算出的e值（用vpa函数显示e的精确值）。
任务2 : 如果要计算出e的小数点后10的精确值，如要算到多少项目？
提示1：如果要求计算出的e的值精确到小数点后10位，则其和真实的exp(1)之间的差要小于0.0000000001.
提示2，编程时可能会用到阶乘，MATLAB里阶乘的函数为 factorial( )
当n>=1时，factorial(n) 等价于 prod([1:n])
如12的阶乘：
factorial(12) % 12的阶乘已经很大了
ans =
479001600
%任务1
clear
my_e=0;
n=0;
while (1/factorial(n))>0.000001
my_e=my_e+1/factorial(n);
n=n+1;
end
vpa(my_e,10)
%任务2
clear
my_e=0;
n=0;
while abs(my_e-exp(1))>0.00000000001
my_e=my_e+1/factorial(n);
n=n+1;
end
fprintf('my_e is:%.15f ,exp(1) is :%.15f ,n is %d \n',my_e,exp(1),n-1)
2.5
作业1：编程输出类似如下的乘法口诀表
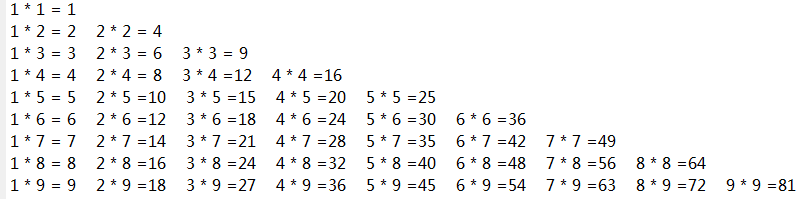
答案：
for n=1:9
for m=1:n
fprintf('%d * %d =%d ',n,m,n*m)
end
fprintf('\n')
end
作业2：求100-999之间的全部水仙花数。
水仙花数是指：一个三位数，其各位数字立方和等于该数本身。例如：370=33+73+03.这就说明370是一个水仙花数。
方法1：循环
for i=1:9
for j=0:9
for k=0:9
num=i*100+j*10+k;
if i^3+j^3+k^3==num
fprintf('找到一个水仙花数，为%d \n',num)
end
end
end
end
方法2：循环
for n=100:999
n_str=num2str(n);
i =str2num(n_str(1));
j =str2num(n_str(2));
k=str2num(n_str(3));
if i^3+j^3+k^3==n
fprintf('找到一个水仙花数，为%d \n',n)
end
end
方法3：向量化编程
x=100:999;
x_1=fix(x/100);
x_2=fix(x/10)-x_1*10;
x_3=fix(x)-x_1*100-x_2*10;
loc=(x==(x_1.^3+x_2.^3+x_3.^3));
x(loc)
作业3：信用卡校验
当你输入信用卡号码的时候，有没有担心输错了而造成损失呢？其实可以不必这么担心，因为并不是一个随便的信用卡号码都是合法的，它必须通过Luhn算法来验证通过。
该校验的过程：
1、从卡号最后一位数字开始，逆向将奇数位(1、3、5等等)相加,得到s1
2、从卡号最后一位数字开始，逆向将偶数位数字，先乘以2（如果乘积为两位数，则将其减去9），再求和,得s2
3、将奇数位总和加上偶数位总和，既s=s1+s2,得出的s应该可以被10整除！如果S不能被10整除，则卡号是错误的。
例如，卡号：5432123456788881
逆向奇数位为 4 2 2 4 6 8 8 1 和 = 35
逆向偶数位乘以2（有些要减去9）的结果：1 6 2 6 1 5 7 7，求和 = 35。
最后 35 + 35 = 70 可以被10整除，则认定校验通过。
请编写一个程序，从标准输入获得卡号，然后判断是否校验通过。
通过显示：“成功”，否则显示“失败”。
比如，输入：356827027232780
程序输出：成功
答案：
x=input('请输入卡号，并以单引号引住这串数字：')
y=x([end:-1:1]) %把字符数组x反向后给y
s_even=0; %偶数位的和的计数器
s_odd=0; %奇数位的和的计数器
L=length(x);
for n=1:2:L %处理奇数位
t1=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
s_odd=s_odd+t1;
end
for n=2:2:L %处理偶数位
t2=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
if t2*2>9
k=t2*2-9;
else
k=t2*2;
end
s_even=s_even+k;
end
total=(s_odd+s_even)
if mod(total,10)==0
fprintf('卡号正确 \n');
else
fprintf('卡号错误 \n');
end
作业4：计算圆周率
利用下列的公式求圆周率PI的值。至少选择以下公式中的2个编程计算圆周率的值。（注意，如果公式里出现阶乘，不要计算太多项，否则计算时间会过长）
这里给出第一个公式的求解代码：
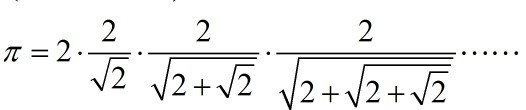
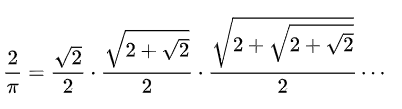
%代码如下：
clear
t=1/2;
x1=sqrt(t);
y1=sqrt(t+t*x1);
for ii=1:20
x1=x1*y1;
y1=sqrt(t+t*y1);
end
p1=2/x1; %p1为我们用公式计算的圆周率
vpa(p1) %vpa显示p1的精确值
vpa(pi,50) %作为对比，用vpa显示真实的π的前50位
计算前20项，已经精确到小数点后12位。
提示：以下公式编程时可能会用到阶乘，MATLAB里阶乘的函数为 factorial( )
factorial(n) 等价于 prod([1:n])
factorial(12) % 12的阶乘已经很大了
ans =
479001600
===============================================
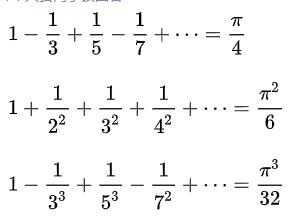
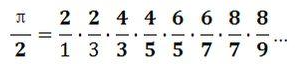
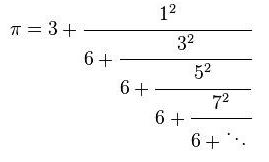
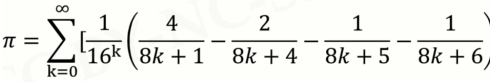
作业5：采用for循环生成如下随机n*m格的彩图
功能1：可以自定义n和m的数量，以及每个格子的像素
功能2：通过循环、pause()函数等技巧，来让如上的随机彩图每隔2秒钟刷新一次，刷新得最终次数自己来确定。需要固定图像，既，需要在imshow后面加hold on命令，以保证每次刷新图像的时候，图像位置固定。
....
imshow(rgb2)
hold on
程序暂停功能——pause()函数使用例子：
x=linspace(0,9,10);
y=sin(x);
for k=1:10
fprintf('当x=%f ,时，对应的y=%f ', x(k),y(k) )
pause()
end
clear all
k=3; %设置网格为k*k
n=100; %设置膨胀倍数n
rgb1=rand(k,k,3); %rgb1的初始化
rgb2=zeros(k*n,k*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k %ii代表行
for jj=1:k %JJ代表列
rgb2((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = repmat(rgb1(ii , jj , : ) ,n ,n );
end
end
imshow(rgb2)
答案：
clear all
k1=input('请输入彩图的行数（1-10之间的正整数）：')
k2=input('请输入彩图的列数（1-10之间的正整数）：')
n=input('请输入每个单元格的像素值（50-100之间的正整数）：')
m=input('请输入彩图的刷新次数（1-100之间的正整数）：')
for t=1:m %刷新m次，每次都重新生成新的随即彩图
rgb1=rand(k1,k2,3); %rgb1的初始化
rgb2=zeros(k1*n,k2*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k1 %ii代表行
for jj=1:k2 %JJ代表列
rgb2((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = repmat(rgb1(ii , jj , : ) ,n ,n );
end
end
imshow(rgb2) %显示彩图rgb2
hold on %保持彩图窗口不动
pause(2) %持续2秒
end
作业1：编程输出类似如下的乘法口诀表
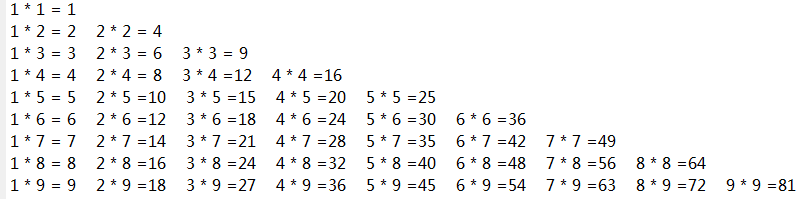
答案：
for n=1:9
for m=1:n
fprintf('%d * %d =%d ',n,m,n*m)
end
fprintf('\n')
end
作业2：求100-999之间的全部水仙花数。
水仙花数是指：一个三位数，其各位数字立方和等于该数本身。例如：370=33+73+03.这就说明370是一个水仙花数。
答案：
方法1：循环
for i=1:9
for j=0:9
for k=0:9
num=i*100+j*10+k;
if i^3+j^3+k^3==num
fprintf('找到一个水仙花数，为%d \n',num)
end
end
end
end
方法2：循环,使用str2num,num2str..
for n=100:999
n_str=num2str(n);
i =str2num(n_str(1));
j =str2num(n_str(2));
k=str2num(n_str(3));
if i^3+j^3+k^3==n
fprintf('找到一个水仙花数，为%d \n',n)
end
end
方法3：向量化编程
x=100:999;
x_1=fix(x/100);
x_2=fix(x/10)-x_1*10;
x_3=fix(x)-x_1*100-x_2*10;
loc=(x==(x_1.^3+x_2.^3+x_3.^3));
x(loc)
方法3：向量化编程--采用mod()函数
x=100:999;
x_1=mod( fix(x/100),10);
x_2=mod( fix(x/10),10);
x_3=mod( x,10);
loc=(x==(x_1.^3+x_2.^3+x_3.^3));
x(loc)
作业3：信用卡校验
当你输入信用卡号码的时候，有没有担心输错了而造成损失呢？其实可以不必这么担心，因为并不是一个随便的信用卡号码都是合法的，它必须通过Luhn算法来验证通过。
该校验的过程：
1、从卡号最后一位数字开始，逆向将奇数位(1、3、5等等)相加,得到s1
2、从卡号最后一位数字开始，逆向将偶数位数字，先乘以2（如果乘积为两位数，则将其减去9），再求和,得s2
3、将奇数位总和加上偶数位总和，既s=s1+s2,得出的s应该可以被10整除！如果S不能被10整除，则卡号是错误的。
例如，卡号：5432123456788881 （其逆向为：1888876543212345）
逆向奇数位为 1 8 8 6 4 2 2 4 ，求和 = 35
逆向偶数位乘以2（有些要减去9）的结果：7 7 5 1 6 2 6 1，求和 = 35。
最后 35 + 35 = 70 可以被10整除，则认定校验通过。
请编写一个程序，从标准输入获得卡号，然后判断是否校验通过。
通过显示：“卡号正确”，否则显示“卡号错误”。
比如，输入：356827027232780
程序输出：卡号正确
提示答案：
x=input('请输入卡号，并以单引号引住这串数字：')
y=x([end:-1:1]) %把字符数组x反向后给y
s_even=0; %偶数位的和的计数器
s_odd=0; %奇数位的和的计数器
for n=1:2:L %处理奇数位
t1=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
？？
end
for n=2:2:L %处理偶数位
t2=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
？？
end
total=(s_odd+s_even)
if ？？
fprintf('卡号正确 \n');
else
fprintf('卡号错误 \n');
end
==================================================================
答案：
x=input('请输入卡号，并以单引号引住这串数字：') %x='123467863265136'
y=x([end:-1:1]) %把字符数组x反向后给y
s_even=0; %偶数位的和的计数器
s_odd=0; %奇数位的和的计数器
L=length(x);
for n=1:2:L %处理奇数位
t1=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
s_odd=s_odd+t1;
end
for n=2:2:L %处理偶数位
t2=str2num(y(n)); %需把字符数组y里面的每个元素转为数字格式
if t2*2>9
k=t2*2-9;
else
k=t2*2;
end
s_even=s_even+k;
end
total=(s_odd+s_even)
if mod(total,10)==0
fprintf('卡号正确 \n');
else
fprintf('卡号错误 \n');
end
作业4：计算圆周率
利用下列的公式求圆周率PI的值。至少选择以下公式中的3个编程计算圆周率的值。（注意，如果公式里出现阶乘，不要计算太多项，否则计算时间会过长）
这里给出第一个公式的求解代码：
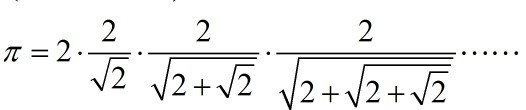
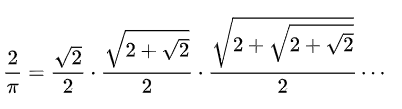
%代码如下：
clear
t=1/2;
x1=sqrt(t);
y1=sqrt(t+t*x1);
for ii=1:20
x1=x1*y1;
y1=sqrt(t+t*y1);
end
p1=2/x1; %p1为我们用公式计算的圆周率
vpa(p1) %vpa显示p1的精确值
vpa(pi,50) %作为对比，用vpa显示真实的π的前50位
计算前20项，已经精确到小数点后12位。
提示：以下公式编程时可能会用到阶乘，MATLAB里阶乘的函数为 factorial( )
factorial(n) 等价于 prod([1:n])
factorial(12) % 12的阶乘已经很大了
ans =
479001600
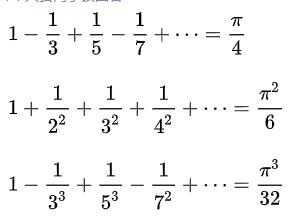
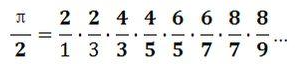
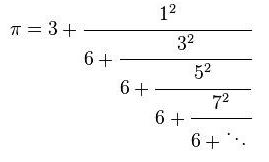
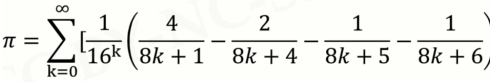
作业5：采用for循环生成如下随机n*m格的彩图
功能1：可以自定义n和m的数量，以及每个格子的像素
功能2：通过循环、pause()函数等技巧，来让如上的随机彩图每隔2秒钟刷新一次，刷新得最终次数自己来确定。需要固定图像，既，需要在imshow后面加hold on命令，以保证每次刷新图像的时候，图像位置固定。
....
imshow(rgb2)
hold on
程序暂停功能——pause()函数使用例子：
x=linspace(0,9,10);
y=sin(x);
for k=1:10
fprintf('当x=%f ,时，对应的y=%f ', x(k),y(k) )
pause()
end
clear all
k=3; %设置网格为k*k
n=100; %设置膨胀倍数n
rgb1=rand(k,k,3); %rgb1的初始化
rgb2=zeros(k*n,k*n,3); %rgb2的初始化
%下面开始膨胀操作。
for ii=1:k %ii代表行
for jj=1:k %JJ代表列
？
end
end
imshow(rgb2)
答案：
clear all
k1=input('请输入彩图的行数（1-10之间的正整数）：')
k2=input('请输入彩图的列数（1-10之间的正整数）：')
n=input('请输入每个单元格的像素值（50-100之间的正整数）：')
m=input('请输入彩图的刷新次数（1-100之间的正整数）：')
rgb=zeros(k1*n,k2*n,3); %rgb的初始化
for t=1:m %刷新m次，每次都重新生成新的随即彩图
for ii=1:k1 %ii代表行
for jj=1:k2 %JJ代表列
rgb((ii-1)*n+1:ii*n , (jj-1)*n+1:jj*n , : ) = ones(n ,n ,3).*rand(1,1,3);
end
end
imshow(rgb) %显示彩图rgb
hold on %保持彩图窗口不动
pause(2) %持续2秒
end
文字谜：山青与水秀x美=秀水与青山
其中“山青与水秀美”为1-9中的其中6个不同的数字，把这个6个数字编程找出来。
%方法1
A=[1:9]
for x1=A
for x2=setdiff(A,x1)
for x3=setdiff(A,[x1,x2])
for x4=setdiff(A,[x1,x2,x3])
for x5=setdiff(A,[x1,x2,x3,x4])
for x6=setdiff(A,[x1,x2,x3,x4,x5])
s1=x1*10000+x2*1000+x3*100+x4*10+x5;
k=x6;
s2=x5*10000+x4*1000+x3*100+x2*10+x1;
if s1*k==s2
fprintf('%d*%d = %d \n',s1,k,s2)
end
end
end
end
end
end
end
%方法2
for n=12345:50000
k1=n;
s=num2str(n);
k2=str2num(s([end:-1:1]));
for d=2:9
if k1*d==k2
n
d
break
end
end
end
作业：图像的马赛克处理
马赛克的原理，就是把一个区域内的所有像素的值统一成一个值，消除像素之间的差异性。
要求：（1）先把一张彩色图片转换成灰度图。（2）把图片的行数和列数截取为100的整数倍，比如：如果图片大小为630*540，则保留为600*500。
（3）把该灰度图按照20*20像素区块进行马赛克化处理。然后显示原图与马赛克化后的对比图。
效果如下图：
clear all;
pic_rgb=imread('D:\pic1.jpg'); %读入彩色图
w=50 %设置每个马赛克块的宽度
[row,col,d]=size(pic_rgb) %测量彩色图的size
pic_r =pic_rgb(:,:,1); %抽取R通道的矩阵给变量pic_r
pic_g=pic_rgb(:,:,2); %抽取G通道的矩阵给变量pic_b
pic_b=pic_rgb(:,:,3); %抽取B通道的矩阵给变量pic_g
pic_gray=pic_r*0.299 +pic_g*0.587+pic_b*0.114; %利用心理学公式合成
row_new=fix(row/100)*100;
col_new=fix(col/100)*100;
pic_msk=pic_gray(1:row_new,1:col_new); %初始化马赛克图，即从灰度图里截取100的整数倍
for n=1:w:row_new
for m=1:w:col_new
p_tem=pic_msk(n:n+w-1,m:m+w-1);
p_tem_mean=uint8(mean(p_tem(:)));
pic_msk(n:n+w-1,m:m+w-1)=p_tem_mean;
end
end
subplot(1,2,1), imshow(pic_gray)
subplot(1,2,2), imshow(pic_msk)
2.6作业：
作业1：设计一个函数，调用此函数可以返回矩阵（或者数组）中最大值以及最小值元素和平均值等。
function [ma,mi,ma_R,ma_C,mi_R,mi_C,pjz] = mymaxmin(A)
%此函数的功能是找到矩阵中的最大值及最小值，以及这两个最值对应的坐标。
[n,m]=size(A)
........
end
输入参数A为输入的一个矩阵或者数组。
返回参数ma,mi为找到的矩阵A中的最大值与最小值。
返回参数ma,mi,ma_R,ma_C,mi_R,mi_C为最大值与最小值所对应的行号和列号。
返回参数pjz为矩阵A中的平均值。
要求：不能用matlab自带的max/min等现成的函数，要自己用for循环、if判断、>=,等方式寻找最大与最小值。
效果如下：
用正态分布的随机矩阵（20行400列）测试：
自己手写一个求数组最大值的代码，代替matlab自带的max()函数。供参考
x=randi(50,1,15)
ma=-inf
for j=1:1
for k=1:15
if x(j,k)>ma
ma=x(j,k);
end
end
end
ma
答案：
function [ma,mi,ma_R,ma_C,mi_R,mi_C,pjz] = mymaxmin(A)
%此函数的功能是找到矩阵中的最大值及最小值，以及这两个最值对应的坐标。
[m,n]=size(A);
ma=-inf;
mi=inf;
total=0;
for i=1:m
for j=1:n
if A(i,j)>ma
ma=A(i,j);
ma_R=i;
ma_C=j;
end
if A(i,j)<mi
mi=A(i,j);
mi_R=i;
mi_C=j;
end
total=total+A(i,j);
end
end
pjz=total/(m*n);
end
作业2：试着看看能否自己设计一个函数，比如命名为myfind.m, 实现matlab自带的find函数的类似功能？
function [ A_k , A_k_R , A_k_C ] = myfind(A , k , w )
%此函数的功能是找到矩阵A中的大于k（当W=1时），或者小于k（当W=0时）的元素。
.......
end
输入参数A为输入的一个矩阵或者数组。
输入参数W只能为1或者0；k=1时找到矩阵A中的大于等于k的所有元素，k=0时找到矩阵A中的小于等于k的所有元素。
返回参数 A_k , A_k_R , A_k_C为3个数组，分别记录按照要求找到的元素，以及这些元素对应的行号和列号 。
要求：
（1）不能用matlab自带的find等现成的函数，要自己用for循环、if判断、>=,等方式寻找最大与最小值。
（2）如果对方输入的参数w 不是0或者1，则要求对方重新输入正确的值。
（3）如果没有找人任何符合要求的元素，则打印输出一句话“很抱歉，没有找到符合条件的元素。”
基本测试：
输入参数有误时的测试：
答案：
function [ A_k , A_k_R , A_k_C ] = myfind(A , k , w )
%此函数的功能是找到矩阵A中的大于k（当W=1时），或者小于k（当W=0时）的元素。
while ( w~=0)&( w~=1)
fprintf('输入有误，w的值必须是0或者1 \n');
w =input('请重新输入 w =');
end
[m,n]=size(A);
A_k=[];
if w==1
fprintf('即将为您寻找矩阵%c %c %f 的所有元素。 \n' ,'A' ,'>',k);
Num=0;
for ii=1:m
for jj=1:n
if A(ii,jj)>=k
Num=Num+1;
A_k(Num)=A(ii,jj);
A_k_R(Num)=ii;
A_k_C(Num)=jj;
end
end
end
end
if w==0
fprintf('即将为您寻找矩阵%c %c %f 的所有元素。 \n' ,'A' ,'<',k);
Num=0;
for ii=1:m
for jj=1:n
if A(ii,jj)<=k
Num=Num+1;
A_k(Num)=A(ii,jj);
A_k_R(Num)=ii;
A_k_C(Num)=jj;
end
end
end
end
end
作业3：编写一个名为is_prim()的函数。调用方式为 y=is_prim(n)
此函数可以实现的功能为：对输入的一个大于1的整数n进行判断其是否是素数，如果是素数则返回y=1，否则返回y=0（并给出原因，比如该数可以分解成某两个大于1的整数的乘积）
function y = is_prime(N)
%子函数 is_prime(N)用于判断给定的数N是否是素数
%如果给定的N是素数，则返回1，否则返回0
flag=0; %用flag来记录N的因子的个数，初始值为0
m=fix(sqrt(N)); %寻找N的因子时，只需要试到fix(sqrt(N))
for k=2:m
if mod(N,k)==0 %如果能被2-m之间的某个数整除，说明找到了一个因子
flag=flag+1; %因子记录器加1
break %跳出循环，节约时间
end
end
if flag==0 %如果flag==0 ，说明前面没有找到N的因子，既N是素数，返回1
y=1;
else
y=0;
end
end
作业4：编写一个名为函数zxgbs(X1,X2)的函数，
实现求最小公倍数的功能，即调用该函数，输入两个正整数x1,x2,则返回这两个正整数的最小公倍数。如:zxgbs(10,15)，则返回y=30;
提示：两个正整数的最小公倍数，等于，这两个正整数的乘积，除以这两个正整数的最大公约数。最大公约数可以使用for循环来寻找
y = zxgbs(10,15)
function y = zxgbs(x1,x2)
%函数zxgbs(x1,x2) 用于计算x1和x2的最小公倍数
M=fix(min(x1,x2)/2); %只需计算到x1和x2中最小那个的一半即可
zdgys=1; %最大公约数初始化为1
for k=2:M
if rem(x1,k)==0&rem(x2,k)==0 %如果k能同时整除x1和x2
zdgys=k %则把最大公约数更新为k
end
end
y=x1*x2/zdgys;
end
作业5：编写一个彩色图像的马赛克处理函数
调用格式为 p_msk = mymsk( pic , w ) ，pic为输入的原始彩色图片，W为马赛克的宽度，p_msk为函数处理后输出的马赛克处理后的图片。
mymsk函数内部处理过程：
步骤1：把图片的行数和列数截取为100的整数倍，得到pic_new，比如：如果原始图片大小为630*540，则pic_new为600*500。
步骤2：把输入的彩色图片pic_new的r,g,b三个通道抽出,分别给pic_new_r, pic_new_g, pic_new_b,。
步骤3：分别把pic_new_r, pic_new_g, pic_new_b这三个灰度图,按照w*w像素区块进行马赛克化处理,得到三个马赛克化后的图；
步骤4：再把步骤3得到的三个通道的马赛克图利用cat()函数重新拼接成一个彩色图p_msk；
在主程序中调用后的效果如下图：
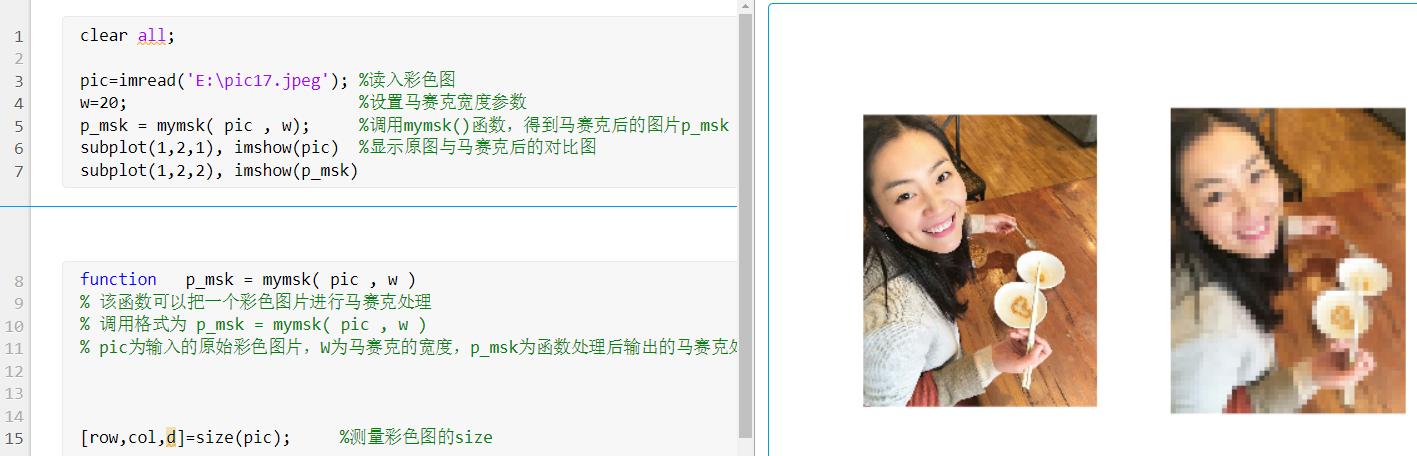
clear all;
pic=imread('E:\pic17.jpeg'); %读入彩色图
w=20; %设置马赛克宽度参数
p_msk = mymsk( pic , w); %调用mymsk()函数，得到马赛克后的图片p_msk
subplot(1,2,1), imshow(pic) %显示原图与马赛克后的对比图
subplot(1,2,2), imshow(p_msk)
function p_msk = mymsk( pic , w )
% 该函数可以把一个彩色图片进行马赛克处理
% 调用格式为 p_msk = mymsk( pic , w )
% pic为输入的原始彩色图片，W为马赛克的宽度，p_msk为函数处理后输出的马赛克处理后的图片。
[row,col,d]=size(pic); %测量彩色图的size
row_new=fix(row/100)*100;
col_new=fix(col/100)*100;
pic_new=pic(1:row_new,1:col_new,:); %初始化马赛克图，即从灰度图里截取100的整数倍
pic_new_r = pic_new(:,:,1); %抽取R通道的矩阵给变量pic_r
pic_new_g = pic_new(:,:,2); %抽取G通道的矩阵给变量pic_b
pic_new_b = pic_new(:,:,3); %抽取B通道的矩阵给变量pic_g
for n=1:w:row_new
for m=1:w:col_new
p_tem_r=pic_new_r(n:n+w-1,m:m+w-1); %抠出当前处理的20*20的区域给p_tem
p_tem_mean_r=uint8(mean(p_tem_r(:))); %求p_tem中的平均值，然后再转换成uint8格式
pic_new_r(n:n+w-1,m:m+w-1)=p_tem_mean_r; %把这个平均值重新赋值给当前的20*20区域
p_tem_g=pic_new_g(n:n+w-1,m:m+w-1); %抠出当前处理的20*20的区域给p_tem
p_tem_mean_g=uint8(mean(p_tem_g(:))); %求p_tem中的平均值，然后再转换成uint8格式
pic_new_g(n:n+w-1,m:m+w-1)=p_tem_mean_g; %把这个平均值重新赋值给当前的20*20区域
p_tem_b=pic_new_b(n:n+w-1,m:m+w-1); %抠出当前处理的20*20的区域给p_tem
p_tem_mean_b=uint8(mean(p_tem_b(:))); %求p_tem中的平均值，然后再转换成uint8格式
pic_new_b(n:n+w-1,m:m+w-1)=p_tem_mean_b; %把这个平均值重新赋值给当前的20*20区域
end
end
p_msk=cat(3,pic_new_r,pic_new_g,pic_new_b);
end
作业：素数问题
（1）编写函数求解给定整数N之内的所有素数；
要求：采用主函数与子函数的模式，子函数is_prime(K)用来判断k是否是素数，如果是，则返回1，否则返回0；主函数则用来遍历2-N之间的每一个整数，如果该数是素数则记录到数组中，并且计数器加1，最终函数返回记录了N之内的所有素数的数组，以及素数的个数。
以下为（1）的提示性代码，供参考；
function [prime,num] = prime_N(N) %主函数prime_N()
%此函数用于找出给定的N之内的所有素数
% 函数[prime,num] = prime_N(N) 中，返回的数组prime记录了N之内的所有素数，
%num记录了N之内的素数的总数。
num=0; %Num记录发现的素数的个数，初始值为0
%采用for循环，挨个判断2-N之间的每一个数是否为素数。
%判断某个数是否为素数的任务通过调用子函数is_prime() 完成。
end
function y = is_prime(N) %子函数is_prime()
%子函数is_prime(N)用于判断给定的数N是否是素数
%如果给定的N是素数，则返回1，否则返回0
flag=0; %用flag来记录N的因子的个数，初始值为0
m=fix(sqrt(N)); %寻找N的因子时，只需要试到fix(sqrt(N))
%for循环来历遍2-m之间的所有数，如果N能被2-m之间的某个数整除，说明找到了一个因子，则因子记录器flag加1，并跳出循环
%如果flag==0 ，说明前面没有找到N的因子，既N是素数，返回1，否则返回0
end
调用效果如下：
（2）编写脚本文件，通过调用prime_N（）函数，找出1000之内的所有孪生素数对，并输出这些孪生素数对。
% 该问的提示性代码：
N=1000;
[prime,num] = prime_N(N)
total=0;
for k=1:num-1
if ？？
total=total+1;
fprintf('找到一对孪生素数:%d , %d \n' ,prime(k), prime(k+1) );
end
end
fprintf('%d 之内共找到%d对孪生素数 \n' ,N, total );
效果如下：
答案：
%调用代码
N=1000;
[prime,num] = prime_N(N)
total=0;
for k=1:num-1
if prime(k+1)-prime(k)==2
total=total+1;
fprintf('找到一对孪生素数:%d , %d \n' ,prime(k), prime(k+1) );
end
end
fprintf('%d 之内共找到%d对孪生素数 \n' ,N, total );
=======================================================
%函数代码
function [prime,num] = prime_N(N) %主函数
%此函数用于找出给定的N之内的所有素数
% 函数[prime,num] = prime_N(N) 中，返回的数组prime记录了N之内的所有素数，
%num记录了N之内的素数的总数。
while N<2|mod(N,1)~=0 %用于保证输入的参数N必为大于1的正整数
N=input('请输入一个大于等于2的正整数')
end
num=0; %Num记录发现的素数的个数，初始值为0
for k=2:N
if is_prime(k)==1 %调用子函数prime_pd(k)，来判断k是否为素数
num=num+1; %如果是素数，则计数器加1
prime(num)=k; %并把素数k存到数组 prime中
end
end
end
function y = is_prime(N)
%子函数 is_prime(N)用于判断给定的数N是否是素数
%如果给定的N是素数，则返回1，否则返回0
flag=0; %用flag来记录N的因子的个数，初始值为0
m=fix(sqrt(N)); %寻找N的因子时，只需要试到fix(sqrt(N))
for k=2:m
if mod(N,k)==0 %如果能被2-m之间的某个数整除，说明找到了一个因子
flag=flag+1; %因子记录器加1
break %跳出循环，节约时间
end
end
if flag==0 %如果flag==0 ，说明前面没有找到N的因子，既N是素数，返回1
y=1;
else
y=0;
end
end
3X+1猜想：
%版权：gdcp_ccl_20210601
clear all
N=input('input='); %比如6171
N=abs( fix(N) ); %或者： N=uint32(N) ; 防止有人输入的数有小数点，或者是负数。
m=[]; %用数组m来存储3x+1序列中的各个数
k=1; %k表示数组m的下标，初始值为1
m(k)=N; %显然，数组m中的第一个元素为N
%生成3x+1序列
while m(k)~=1 %如果数组m中当前元素不为1，则继续，否则停止计算
if mod(m(k),2)~=0 %如果当前元素为奇数，则乘三加一
m(k+1)=3*m(k)+1;
else %如果当前元素为偶数，则除2
m(k+1)=m(k)/2;
end
k=k+1; %下标加1，把下一个元素当成“当前”元素。
end
%计算3x+1序列中的长度,最大值，最大值和输入值之间的比例
L=numel(m);
m_max=max(m);
Ratio=m_max/N;
%输出3x+1序列，每行10个
for k=1:L
fprintf('%8d',m(k))
if mod(k,10)==0 %每输出10个，回车一次
fprintf('\n')
end
end
fprintf('\n')
%输出3x+1序列的相关参数
fprintf('数字%d的3x+1序列长度 = %d \n', N,L );
fprintf('数字%d的3x+1序列中的最大值 = %d \n', N,m_max );
fprintf('数字%d的3x+1序列中的最大值与初始值的比值为 = %d \n', N,Ratio );
plot(m,'*-') %画出该数字的3x+1序列的图
作业4：编写一个中值滤波函数：zzlb() , 用于滤除图像的椒盐噪声
%以下代码为提示性代码：
function pic_new=zzlb(pic_old)
% 本函数可以对充满椒盐噪声的图像进行滤波，返回滤除椒盐噪声后的干净图像
%函数pic_new=zzlb(pic_old)中，输入参数pic_old为含有椒盐噪声的原始图像（uint8格式）
%函数返回值pic_new则为消除了椒盐噪声后的干净图像
[n,m,d]=size(pic_old) %获取图像pic_old的维度
%判断d等1还是等于3？如果等于1，则pic_old为灰度图，执行以下操作
%对pic_old进行边界填充，得到膨胀了一圈的图像pic2（n+2行，m+2列）
%采用双层for循环，对pic2进行中值滤波，得到滤波后的干净图像pic3
%把pic3瘦一圈，变成n行m列后，赋值给pic_new
for i=2:n+1
for j=2:m+1
..........
..........
..........
%如果d=3,则表示pic_old为彩色图，这时，需要对RBG每一个通道都进行上述类似的中值滤波，
%得到3个滤波后的2维数组，再合并成一个3维数组，即彩色的pic_new
..........
..........
..........
end
========================================
答案：
function p_new = zzlb(p_noise)
% 本函数可以对充满椒盐噪声的图像进行滤波，返回滤除椒盐噪声后的干净图像
%函数pic_new=zzlb(p_noise)中，输入参数p_noise为含有椒盐噪声的原始图像（uint8格式）
%函数返回值pic_new则为消除了椒盐噪声后的干净图像
%版权：gdcp_ccl_2021_05_25
p_new =p_noise; %p_noise用于被观察，修改则在p_new上进行，两者功能分开
[row,col,d]=size(p_noise); %测量输入图像的尺寸
if d==1
%对原始图像p_noise边界填充生成胖一圈的图像p，在p上进行历遍操作
p=[ p_noise(1,1) , p_noise(1,:) , p_noise(1,col);
p_noise(:,1) , p_noise , p_noise(:,col);
p_noise(row,1), p_noise(row,:) , p_noise(row,col)];
for n=2:row+1 %在新图p的2到row+1行，2到col+1列的区域历遍（即原图范围）
for m=2:col+1
if p(n,m)==255|p(n,m)==0 %如果当前点为极端值（0或255）
tem=p(n-1:n+1,m-1:m+1); %以当前点为中心，构建一个3*3的临时矩阵
md=median(tem(:)); %找出这个矩阵所有元素的中位数
p_new(n-1,m-1)=md; %则用刚才找到的中位数代替该极端值
end
end
end
end
if d==3 %如果是rgb彩图，则拆解成三个通道，对每个通道分别进行中值滤波
p_new(:,:,1) = zzlb(p_noise(:,:,1)); %红通道递归调用zzlv函数，进行降噪
p_new(:,:,2) = zzlb(p_noise(:,:,2)); %绿通道递归调用zzlv函数，进行降噪
p_new(:,:,3) = zzlb(p_noise(:,:,3)); %蓝通道递归调用zzlv函数，进行降噪
end
end
调用和使用上述函数，示例：
p_noise=imread('D:\matlab2021\pic\yujinxiang_rgb_saltpepper.png');
p_new = zzlb(p_noise);
subplot(1,2,1),imshow(p_noise);
subplot(1,2,2),imshow(p_new);
如果不扩边，则答案：
%调用代码
p_noise=imread('C:\Users\Administrator\Desktop\p2.png'); %读入带噪点的图像，作为矩阵给p_noise
p_new = zzlb(p_noise); %用zzlb函数处理带噪声的图像p_noise，生成干净的图像给p_new
subplot(1,2,1),imshow(p_noise); %子图1，显示原始的带噪声的图像p_noise
subplot(1,2,2),imshow(p_new); %子图2，显示干净的图像p_new
========================================================
%函数代码
function p_new = zzlb(p_noise)
% 本函数可以对充满椒盐噪声的图像进行滤波，返回滤除椒盐噪声后的干净图像
%函数pic_new=zzlb(p_noise)中，输入参数p_noise为含有椒盐噪声的原始图像（uint8格式）
%函数返回值pic_new则为消除了椒盐噪声后的干净图像
p_new =p_noise; %p_noise用于被观察，修改则在p_new上进行，两者功能分开
[row,col,d]=size(p_noise); %测量图像的尺寸
if d==1 %灰度图时的处理方式
for n=2:row-1 %在p_noise的2到row-1行、2到col-1列的区域历遍
for m=2:col-1
if p_noise(n,m)==255|p_noise(n,m)==0 %如果当前点为极端值（0或255），既噪声。
tem=p_noise(n-1:n+1,m-1:m+1); %以当前点为中心，构建一个3*3的临时矩阵
md=median(tem(:)); %找出这个矩阵所有元素的中位数
p_new(n,m)=md; %则用刚才找到的中位数代替该极端值
end
end
end
end
if d==3 %如果是rgb彩图，则拆解成三个通道，对每个通道分别进行中值滤波
p_new(:,:,1) = zzlb(p_noise(:,:,1)); %红通道递归调用zzlv函数，进行降噪
p_new(:,:,2) = zzlb(p_noise(:,:,2)); %绿通道递归调用zzlv函数，进行降噪
p_new(:,:,3) = zzlb(p_noise(:,:,3)); %蓝通道递归调用zzlv函数，进行降噪
end
end
作业所用含椒盐噪声图像如下：
3X+1猜想：
%版权：gdcp_ccl_20210601
clear all
N=17 %比如17
m=[]; %用数组m来存储3x+1序列中的各个数
k=1; %k表示数组m的下标，初始值为1
m(k)=N; %显然，数组m中的第一个元素为N
%生成3x+1序列
while m(k)~=1 %如果数组m中当前元素不为1，则继续，否则停止计算
if mod(m(k),2)~=0 %如果当前元素为奇数，则乘三加一
m(k+1)=3*m(k)+1;
else %如果当前元素为偶数，则除2
m(k+1)=m(k)/2;
end
k=k+1; %下标加1，把下一个元素当成“当前”元素。
end
%计算3x+1序列中的长度,最大值，最大值和输入值之间的比例
L=numel(m);
m_max=max(m);
Ratio=m_max/N;
%输出3x+1序列，每行10个
fprintf('数字%d的3X+1序列如下： \n ',N)
for k=1:L
fprintf('%8d',m(k))
if mod(k,10)==0 %每输出10个，回车一次
fprintf('\n ')
end
end
fprintf('\n')
%输出3x+1序列的相关参数
fprintf('数字%d的3x+1序列长度 = %d \n ', N,L );
fprintf('数字%d的3x+1序列中的最大值 = %d \n ', N,m_max );
fprintf('数字%d的3x+1序列中的最大值与初始值的比值为 = %d \n ', N,Ratio );
plot(m,'*-') %画出该数字的3x+1序列的图
第三章作业
第四章作业
