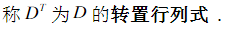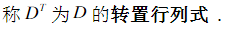暂无搜索结果
-
1 线性方程组
-
1.1 线性方程组的基本概念
-
1.2 高斯消元法与阶梯型
-
1.3 线性方程组的等价与初等变换
-
1.4 矩阵
-
1.5 齐次线性方程组
-
1.6 二阶行列式
-
1.7 三阶行列式
-
2 集合与映射
-
2.1 集合的基本概念
-
2.2 集合之间的运算
-
2.3 集合的乘积和基数
-
2.4 映射的基本概念
-
2.5 映射的合成
-
2.6 逆映射
-
2.7 对换
-
2.8 置换的分解
-
2.9 例子
-
2.10 置换的符号
-
2.11 偶置换与奇置换
-
2.12 置换在函数上的作用
-
2.13 等价关系
-
2.14 商映射与序关系
-
2.15 数学归纳法
-
2.16 整数的算术(上)
-
2.17 整数的算术(下)
-
3 矩阵
-
3.1 向量和向量空间
-
3.2 线性组合和线性相关
-
3.3 一些性质
-
3.4 基
-
3.5 维数
-
3.6 行秩、列秩的定义及性质
-
3.7 线性方程组的可解性准则
-
3.8 重新理解线性方程组
-
3.9 线性映射
-
3.10 矩阵的运算
-
3.11 矩阵乘积的秩
-
3.12 矩阵的转置
-
3.13 单位矩阵和纯量矩阵
-
3.14 可逆矩阵
-
3.15 一些计算
-
3.16 初等矩阵
-
3.17 逆矩阵的计算
-
3.18 线性方程组的解空间
-
3.19 解空间的基础解系
-
4 行列式
-
4.1 平行六面体的体积与行列式
-
4.2 行列式的若干性质
-
4.3 广义行列式函数
-
4.4 行列式按一行或一列的元素展开
-
4.5 准三角方阵的行列式
-
4.6 方阵乘积的行列式
-
4.7 例子
-
4.8 可逆矩阵的行列式判别准则
-
4.9 克拉默法则
-
4.10 矩阵的子式与矩阵的秩的联系
-
5 群、环、域
-
5.1 运算
-
5.2 结合律的性质
-
5.3 幂与倍数
-
5.4 可逆元素
-
5.5 群的定义和例子
-
5.6 循环群
-
5.7 元素的阶
-
5.8 循环群的子群
-
5.9 同态与同构
-
5.10 例子与结论
-
5.11 半群的乘法表以及群与对称
-
5.12 环的定义和例子
-
5.13 整数的剩余类环
-
5.14 零因子、整环
-
5.15 同态
-
5.16 域的定义,例子
-
5.17 素域
-
5.18 域的特征
-
5.19 任意域上的线性方程组
-
6 复数和多项式
-
6.1 复数域
-
6.2 矩阵模型
-
6.3 复平面、棣莫弗公式
-
6.4 共轭
-
6.5 实数域二次扩张的唯一性
-
6.6 有理数域的二次扩张
-
6.7 复数的初等几何
-
6.8 尺规作图与二次扩张
-
6.9 定义
-
6.10 一些术语
-
6.11 多项式的取值
-
6.12 带余除法
-
6.13 多元多项式
-
6.14 多元单项式的字典序
-
6.15 若干术语
-
6.16 整除的初等性质
-
6.17 最大公因子和最小公倍元
-
6.18 欧几里得环的唯一因子分解性
-
6.19 整系数多项式的因式分解
-
6.20 整环的分式域
-
6.21 欧几里得环的分式域
-
6.22 有理函数域
-
7 多项式的根
-
7.1 根与线性因子
-
7.2 韦达公式
-
7.3 多项式的导数与根的重数
-
7.4 重因子
-
7.5 多项式函数
-
7.6 代数基本定理的叙述和一些引理
-
7.7 代数基本定理的证明
-
7.8 实系数多项式的虚根
-
7.9 复数域和实数域上的最简分式
-
7.10 实系数多项式的根(上)
-
7.11 实系数多项式的根(中)
-
7.12 实系数多项式的根(下)
-
7.13 斯图姆定理的证明
-
7.14 正根的个数与系数的关系
-
7.15 多项式根的近似计算
-
7.16 整系数多项式的有理根
-
7.17 对称多项式的定义与例子
-
7.18 对称多项式的基本定理
-
7.19 待定系数法
-
7.20 一元四次方程的求根问题
-
7.21 判别式
-
7.22 解三次方程
-
7.23 结式(上)
-
7.24 结式(下)
-
8 复习
-
8.1 复习(一)
-
8.2 复习(二)
-
8.3 复习(三)
-
8.4 复习(四)
-
9 阅读
-
10 问卷调查
转置行列式

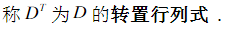

选择班级