考虑平板和带中心圆孔板承受二端均匀拉伸的情况。

图4.20中平板受拉时，中截面aa由于二端对称性仍保持在aa处，截面bb则移至b'b'，截面aa与bb间的任一线段都发生了相同的伸长。如图4.20（a）所示。其线应变为：

ε=bb′/ab=const.

这一结果可以由实验测量截面a、b间线段长度的改变而证明；或直接用电阻应变片测量截面aa上的应变，更精确地证明截面aa上各点的应变ε=const.。

弹性小变形时材料服从虎克定律σ=Eε，故有ε=const，即正应力ε在横截面上均匀分布，如图4.20（b），且

 σ=FN/A=σave

即均匀拉压变形时横截面应力σ等于平均应力σave。这正是前面讨论杆的拉伸与压缩时的结果。

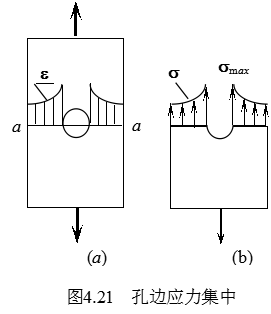
再考虑图4.21中带中心圆孔的平板受拉。此时，沿截面aa上各点测得的应变ε如图4.21(a)所示。ε显然不再是均匀分布的，孔边最大值为ε=εmax。同样可由虎克定律知截面aa上的应力分布也不是均匀的，如图4.21(b)所示，越靠近孔边，应力越大。孔边最大应力为：

σmax=ktσave           ---(4-8)

式中kt>1，是孔边最大应力与平均应力之比，称为弹性应力集中系数。一些常见细节形式的弹性应力集中系数可由手册查出，圆孔边的应力集中系数kt=3。

这一类在构件几何形状改变的局部出现的应力增大现象，称为应力集中。发生应力集中的区域称为应力集中区。当σmax在弹性范围内时，应力集中区最大应力由(4-8)式给出。

在截面几何发生突然改变的位置，如孔、缺口、台阶等处，通常都有应力集中发生。几何改变越剧烈，应力集中越严重。故在必须改变构件几何时，应尽可能用圆弧过渡以减小应力集中的程度。应力集中常常是构件出现裂纹（甚至发生破坏）的重要原因，应当引起注意。