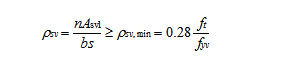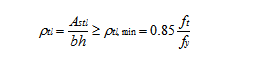7.3 纯扭构件的承载力计算
7.3.1矩形截面纯扭构件的开裂扭矩计算
纯扭构件裂缝出现前处于弹性阶段工作,构件变形及钢筋应力均很小。因此可忽略钢筋对开裂扭矩的影响,按素混凝土构件计算。由材料力学可知,矩形截面匀质弹性材料构件在扭矩作用下,截面中各点均产生剪应力τmax,其分布规律如图7-6。最大剪应力τmax发生在截面长边的中点,与该点剪应力作用相对应的主拉应力σtp和主压应力σcp分别与构件轴线成45°方向,其大小均为τmax。当主拉应力σtp超过混凝土的抗拉强度时,混凝土将沿主压应力方向开裂,并发展成螺旋形裂缝。
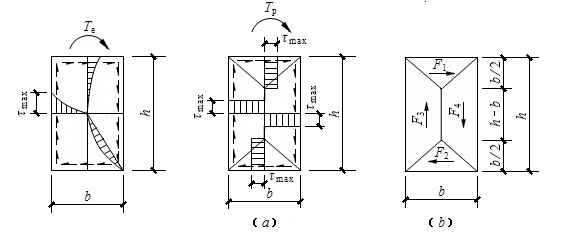
图7-6 矩形截面弹性状态的剪应力分布 图7-7矩形截面塑性状态的剪应力分布
①按照弹性理论:当最大扭剪应力τ或最大主拉应力σtp 达到混凝土抗拉强度ft时的扭矩即为开裂扭矩Tcr :
Tcr =ftWte (7-2)
式中:Wte——截面的受扭弹性抵抗矩,Wte =ab2h;
b、h ——分别为矩形截面的短边和长边尺寸;
a——系数,h/b=1.0时,a =0.208;h/b≈µ时,a =0.33。
②按照塑性理论:当截面某一点的应力到达极限强度时,构件进入塑性状态。该点应力保持在极限应力,而应变可继续增长,荷载仍可增加,直到截面上的应力全部到达材料的极限强度,构件才到达极限承载力。图7-7为矩形截面纯扭构件在全塑性状态时的剪应力分布。截面上的剪应力分为四个区域,分别计算其合力及所组成的力偶,取t =ft,可求得总扭矩T为
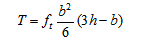 (7-3)
(7-3)
③弹塑性理论:实际上,混凝土既非弹性材料,又非理想塑性材料,而是介于两者之间的弹塑性材料,为了实用,开裂扭矩可按全塑性状态的截面应力分布计算,而将混凝土抗拉强度适当降低。根据试验资料,《结构规范》取混凝土抗拉强度降低系数为0.7,故开裂扭矩的计算式为
Tcr = 0.7 ftWt (7-5)
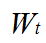 为截面受扭塑性抵抗矩,
为截面受扭塑性抵抗矩, 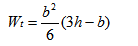
3.矩形截面纯扭构件的承载力计算
承载力计算时采用变角空间桁架模型:忽略中间部分混凝土的抗扭作用,存在螺旋形斜裂缝的混凝土管壁通过纵筋和箍筋的联系形成空间桁架作用抵抗外扭矩。斜裂缝间的混凝土可设想为斜压杆,纵筋为受拉弦杆,箍筋为受拉腹杆。假定桁架节点为铰接,在每个节点处,斜向压力由纵筋和箍筋的拉力所平衡。不考虑裂缝面上的骨料咬合力及钢筋的销栓作用。由于混凝土斜压杆与构件轴线的倾斜角φ,不一定等于45°,而是与配筋强度比z 有关,如图7-8所示。
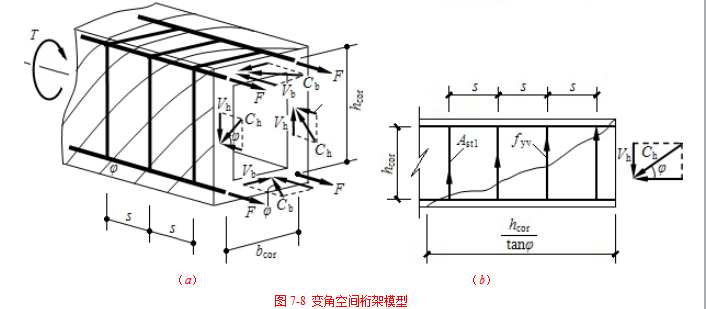
钢筋混凝土纯扭构件试验研究结果表明,构件的抗扭承载力由混凝土的抗扭承载力Tc和钢筋(纵筋和箍筋)的抗扭承载力Ts两部分组成,《规范》考虑到设计应用上的方便,采用略为偏低的表达式
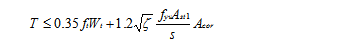 (7-14)
(7-14)
式中:T——扭矩设计值; ft——混凝土的抗拉强度设计值;
Wt——截面的抗扭塑性抵抗矩; fyv——箍筋抗拉强度设计值;
Ast1——箍筋单肢截面面积;s——箍筋间距;Acor——截面核心部分的面积;
z——抗扭纵筋与箍筋的配筋强度比。《混凝土结构设计规范》取z 为0.6≤z≤1.7,当z>1.7 时,取z=1.7。设计中,一般取z=1.0~1.2。
钢筋混凝土矩形截面纯扭构件的配筋计算步骤:先假定z 值,然后按式(7-14)和式(7-1)分别求得箍筋和纵筋用量。
4. T形、工形截面纯扭构件的承载力计算
处理思路:对T形和工字形截面的纯扭构件,可将腹板和翼缘分别进行受扭计算。将整个截面划分为多个矩形截面,并将扭矩T按各个矩形分块的受扭塑性抵抗矩分配,以求得各个矩形分块所承担的扭矩。
划分原则:首先满足腹板矩形截面的完整性,然后再划分受压翼缘或受拉翼缘,如图7-10。所划分的矩形截面抗扭塑性抵抗矩,按表7-1的近似值取用。
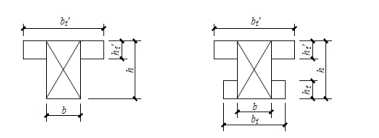
图7-10 T形和工字形截面划分矩形截面方法
表7-1 T形和工字形截面抗扭塑性抵抗矩

所承担的扭矩。当已知腹板、受压翼缘和下翼缘的受扭塑性抵抗矩Wtw、Wtf和Wtf' 时,则各矩形截面所承担的扭矩:为了简化计算,按各矩形截面的受扭塑性抵抗矩的比例来分配截面总扭矩,以确定各矩形截面
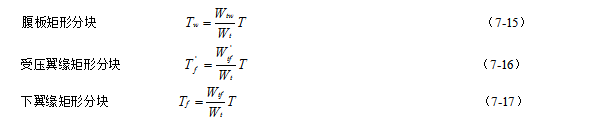
式中:Wt = Wtw+ W 'tf + Wtf ;
T——带翼缘截面所承受的扭矩设计值;
Tw、T'f 、Tf ——分别为腹板、受压翼缘和下翼缘的扭矩设计值。
 5.箱形截面纯扭构件的承载力计算
5.箱形截面纯扭构件的承载力计算
试验表明,具有一定壁厚的箱形截面的受扭承载力与实心截面基本相同。因此,箱形截面受扭承载力公式可以在矩形截面受扭承载力公式的基础上,对Tc项乘以壁厚修正系数αh得出。具体表达式为
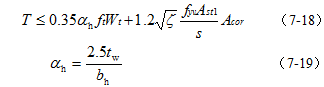
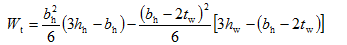 (7-20)
(7-20)
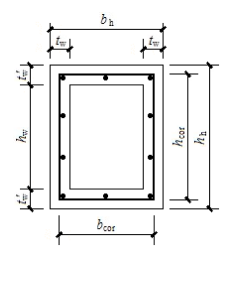
式中:αh——箱形截面壁厚系数,当αh
>1.0时,取αh =1.0;
tw——箱形截面壁厚,其值不应小于bh /7;
hh、bh ——箱形截面的长边和短边尺寸;
hw——箱形截面腹板高度。
6.构造要求
(1)截面尺寸
为了防止构件发生超配筋破坏,截面尺寸应符合如下条件:
T≤0.2βc fc Wt (7-21)
(2)最小配筋率
当T≤0.7ftWt时,截面处于抗裂状态,因此可不进行抗扭承载力计算,按配筋率的下限及构造要求配筋。纯扭构件最小配筋率原则上应根据T=Tcr的条件得出。《结构规范》规定抗扭箍筋的配筋率应满足
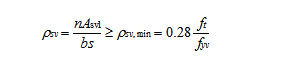 (7-22)
(7-22)
相应地,抗扭纵筋的最小配筋率应满足
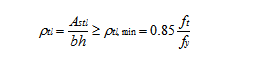 (7-23)
(7-23)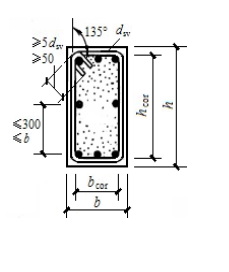
(3)钢筋布置
图7-12为受扭构件的配筋形式及构造要求。由于扭矩引起的剪应力在截面四周最大,并为满足扭矩变号的要求,抗扭钢筋应由抗扭纵筋和抗扭箍筋组成。抗扭纵筋应沿截面周边均匀对称布置,且截面四角处必须放置,其间距不应大于200mm,也不应大于截面宽度b,抗扭纵筋的两端应按受拉钢筋锚固长度要求锚固在支座内。
抗扭箍筋必须采用封闭形式并沿截面周边布置。当采用复合箍筋时,位于截面内部的箍筋不应计入受扭所需的箍筋面积。每边都能承担拉力,故箍筋末端弯钩应大于135°(采用绑扎骨架时),且弯钩端平直长度应大于5dsv(dsv为箍筋直径)和50mm,以使箍筋未端锚固于截面核心混凝土内。抗扭箍筋的直径和最大间距应满足第5章对箍筋的有关规定。
1. 下面哪一条不属于变角度空间桁架模型的基本假定:( A )。
A. 平均应变符合平截面假定;B. 混凝土只承受压力;
C. 纵筋和箍筋只承受拉力;D. 忽略核心混凝土的受扭作用和钢筋的销栓作用;
2. 钢筋混凝土受扭构件中受扭纵筋和箍筋的配筋强度比0.6<ζ<1.7说明,当构件破坏时,( A )。
A. 纵筋和箍筋都能达到屈服;B.仅箍筋达到屈服;
C.仅纵筋达到屈服;D. 筋和箍筋都不能达到屈服。
3. 对受扭构件中抗扭纵筋(B )的说法不正确。
A. 应尽可能均匀地沿截面周边对称布置
B. 在截面的四角可以设抗扭纵筋也可以不设抗扭纵筋
C. 在截面的四角必须设抗扭纵筋
D. 抗扭纵筋间距不应大于300mm,也不应大于截面短边尺寸
4. 对受扭构件中的箍筋,正确的叙述是( C )。
A. 箍筋可以是开口的,也可以是封闭的
B. 箍筋必须封闭且焊接连接,不得搭接
C. 箍筋必须封闭,但箍筋的端部应做成的弯钩,弯钩未端的直线长度不应小于5d和50mm。
D. 箍筋必须采用螺旋箍筋。
【案例】
【7-1】钢筋混凝土矩形截面纯扭构件,承受的扭矩设计值T=20kN×m。截面尺寸b´h=250mm´500mm,混凝土强度等级为C30,纵筋采用HRB335级钢筋,箍筋采用HPB300级钢筋。求此构件所需配置的受扭纵筋和箍筋。
【解】本题属于设计类。
(1)基本参数
查表可知,C30混凝土fc=14.3N/mm2,ft=1.43N/mm2,βc=1.0;HRB335级钢筋fy=300N/mm2,HPB300级钢筋fyv=270N/mm2;
一类环境,c=20mm,bcor=b–2c=200mm,hcor=h–2c=450mm,Acor=200´450=90000mm2。
(2)验算截面尺寸

【作业】
1. 钢筋混凝土矩形截面纯扭构件,截面尺寸b´h=250mm´450mm,一类环境,承受的扭矩设计值T=18kN×m。混凝土强度等级为C30,纵筋采用HRB335级钢筋,箍筋采用直径8mm的HPB300级钢筋。求此构件所需配置的受扭纵筋和箍筋。
2.钢筋混凝土工字形截面纯扭构件,截面尺寸如图7-14示,承受的扭矩设计值
T=28.65kN×m。混凝土强度等级为C30,纵筋采用HRB335级钢筋,箍筋采用HPB300级钢筋。求此构件所需配置的受扭纵筋和箍筋。
3.受扭构件的配筋有哪些构造要求?
4.受扭构件中,受扭纵向钢筋为什么沿截面四周对称放置,并且四角必须放置?
5. 在抗扭计算中如何避免少筋破坏?
6. 抗扭纵筋配筋率与抗弯纵筋配筋率计算有何区别?
7. 纯扭构件承载力计算公式中 的物理意义是什么?起什么作用?
的物理意义是什么?起什么作用?
彩色混凝土——绚丽缤纷的色彩专家
与清水混凝土的素雅朴实相比,绿色混凝土更像一个20出头的小姑娘,爱打扮、花枝招展是它的独特之处。这样的特点也让彩色混凝土被广泛应用于室外装饰、景点改造等公共场所。
不仅如此,彩色混凝土还能使水泥地面永久地呈现各种色泽、图案、质感,逼真地模拟自然的材质和纹理,随心所欲地勾划各类图案,而且愈久弥新,使人们能够轻松地实现建筑物与人文环境、自然环境和谐相处、融为一体。
目前,彩色混凝土已广泛运用于市政步道、园林小路、城市广场、高档住宅小区、停车场、商务办公大楼、户外运动场所(羽毛球场馆、篮球场馆等)。
彩色混凝土的优势:
众口难调,有人喜欢清新素颜的清水混凝土,自然也就有人欣赏多彩艳丽打扮精致的彩色混凝土了。想要体现一个国家或者城市的特色和风格,提升整个城市的形象,这个时候彩色混凝土就充分发挥了其美化城市和诱导交通的作用,她不仅可以与道路周围的建筑艺术完美的协调在一起,更能显示一个现代化都市的气派和魅力。



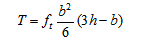
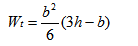

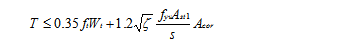


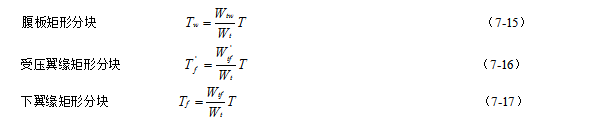

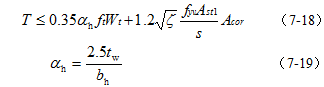
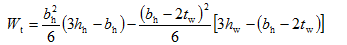 (7-20)
(7-20)