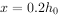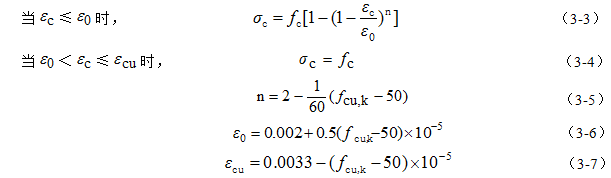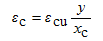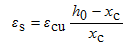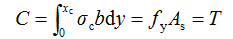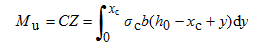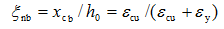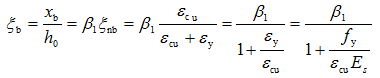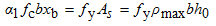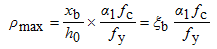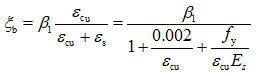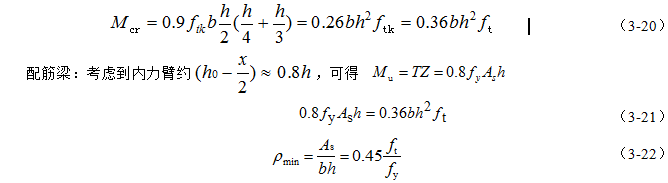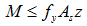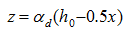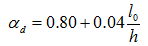3.3 受弯构件正截面承载力计算原理

大家好！这一讲我们学习受弯构件的正截面承载力计算原理。包括4个知识点：①是受弯构件正截面承载力的基本假定；②是基本方程；③是等效矩形应力图；④是适筋梁与超筋梁的界限。

学习要求是：掌握正截面承载力计算的基本假定、适筋梁与超筋梁的界限；理解基本方程的建立方法和等效矩形应力图的原理。

3.3.1 基本原理

 知识点1.基本假定

基于受弯构件的破坏特征分析，正截面承载力计算以图3-6中III_a的应力应变分布作为依据。

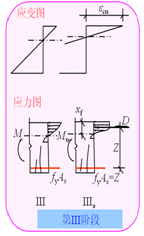
为简化起见，在承载力计算时引入下列四个基本假定：

（1）截面平均应变保持平面；目的是可运用相似三角形原理推到截面上任意一点的应变。

（2）不考虑混凝土的抗拉强度；因为其对弯矩的贡献很小；

（3）混凝土受压的应力与应变关系曲线按下列规定取用（如图3-10），其数学表达式为：

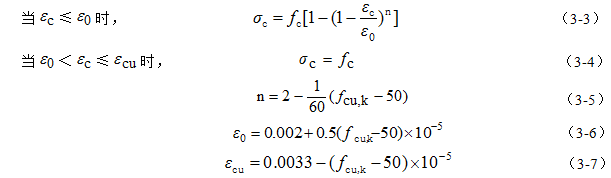
式中：σ_c ——混凝土压应变为ε_c时的压应力；

f_c——混凝土轴心抗压强度设计值；

ε_c——受压区混凝土压应变；

ε₀——混凝土压应力刚达到f_c时的混凝土压应变，当计算的ε₀小于0.002时，取0.002；

ε_cu ——混凝土极限压应变，当处于非均匀受压时，按式（3-8）计算，如计算的ε_cu值大于0.0033，

取0.0033；当处于轴心受压时取ε₀；

f_cu,k ——混凝土立方体抗压强度标准值；

n——系数，当计算的n大于2.0时，取2.0。

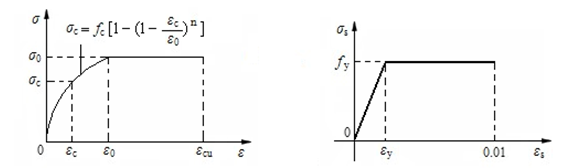
        图3-10 混凝土应力-应变计算曲线                图3-11 钢筋应力-应变计算曲线 

（4）纵向钢筋的应力应变关系曲线如图3-11所示，应力取等于钢筋应变与其弹性模量的乘积，但其值不应大于其相应的强度设计值。纵向受拉钢筋的极限拉应变取为0.01。

知识点2.基本方程

以单筋矩形截面为例，根据上述基本假定可得出截面在承载力极限状态下，受压边缘达到了混凝土的极限压应变ε_cu。若假定这时截面受压区高度为x_c，则

受压区某一混凝土纤维的压应变为 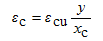                                （3-8）

受拉钢筋的应变为 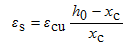                                         （3-9）

将式（3-8）计算的值代入式（3-3）或式（3-4），可得图3-12所示的截面受压区应力分布图形。

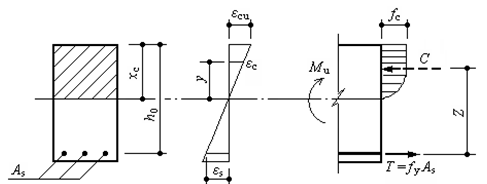
图3-12  受压区混凝土的应力图形

图3-12中，根据截面的基本平衡条件：C=T，得

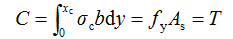                   （3-10）

此时，截面所能抵抗的弯矩，即截面受弯承载力M_u为

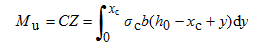                                          （3-13）

式中：Z——C与T之间的距离，称为内力臂。

活学活用以上方法和基本方程，会成为创新的源泉

知识点3.等效矩形应力图

利用上述公式虽然可以计算出截面的抗弯承载力，但计算过于复杂，尤其是当弯矩已知而需确定受拉钢筋的截面面积时，必须经多次试算才能获得满意的结果。因此，需要对受压区混凝土的应力分布图形作进一步的简化。可用图3-13所示的等效矩形应力图形来代替受压区混凝土的曲线应力图形。

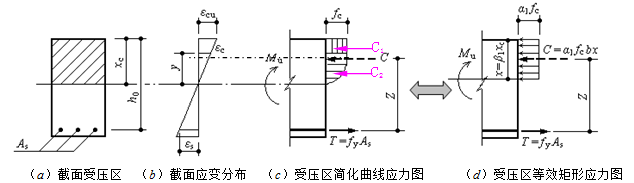
图3-13  等效矩形应力图形的换算

用等效矩形应力图形代替实际曲线应力分布图形时，应满足两个等效条件：①保持原来受压区混凝土压应力合力C的大小不变；②保持原来受压区混凝土压应力合力C的作用点不变。

    等效矩形应力图由无量纲参数α₁和β₁来确定。等效矩形应力图的受压区高度为β₁x_c，受压混凝土强度为α₁f_c，此处x_c为受压区实际高度。β₁和α₁称为等效矩形应力图系数，系数α₁是受压区混凝土矩形应力图的应力值与混凝土轴心抗压强度设计值的比值；系数β₁是矩形应力图受压区高度x与中和轴高度x_c的比值。《规范》建议应力图系数β₁和α₁按表3-2采用。表中数值之间的按直线内插法取用。

                表3-2  受压混凝土的简化应力图形系数β₁和α₁值                

3.3.2适筋梁与超筋梁少筋梁的界限

知识点4.适筋和超筋破坏的界限条件

比较适筋梁和超筋梁破坏，两者的差异在于：前者破坏始自受拉钢筋；后者则始自受压区混凝土。显然，当梁的钢筋级别和混凝土强度等级确定之后，总存在一个特定的配筋率ρ_max，使得钢筋应力到达屈服强度的同时，受压区边缘纤维应变也恰好到达混凝土受弯时极限压应变值，发生“界限破坏”，即适筋梁与超筋梁的界限。鉴于安全和经济的考虑，在实际工程中不允许采用超筋梁，那么这个特定配筋率ρ_max实质上就限制了适筋梁的最大配筋率。梁的实际配筋率ρ＜ρ_max时，破坏始自受拉筋的屈服；ρ＞ρ_max时，破坏始自受压区混凝土的压碎；ρ=ρ_max时，受拉钢筋应力到达屈服强度的同时压区混凝土压碎而使截面破坏。

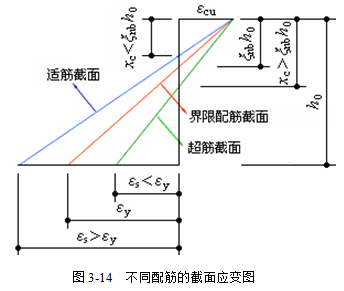
为了防止发生超筋破坏，要求配筋率不超过界限配筋率ρ_max值，或控制ξ不超过界限相对受压区高度ξ_b，其值可根据平截面假定求得。

（1）使用有明显屈服点钢筋的受弯构件

根据给定的混凝土极限压应变ε_cu和平截面假定可知，适筋和超筋的界限破坏，即钢筋达到屈服（ε_y=f_y /E_s）同时混凝土发生受压破坏（ε_c=ε_cu）的相对中和轴高度ξ_nb为（图3-14）：

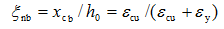                      （3-16）

由x=β₁ x _c的关系，则界限相对受压区高度ξ_b为：

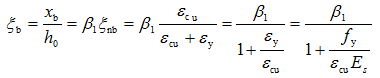                    （3-17a）

由式（3-17a）可知，对不同的钢筋级别和不同混凝土强度等级有着不同的ξ_b值，见表3-3。

                            表3-3  钢筋混凝土构件配有屈服点钢筋的ξ_b值 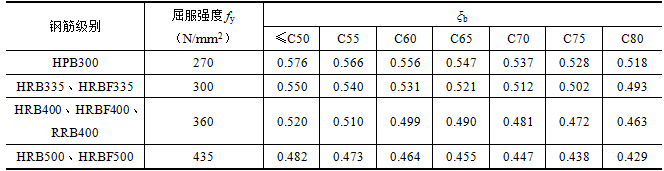                                  当相对受压区高度ξ≤ξ_b时，属于适筋梁；相对受压区高度ξ＞ξ_b时，属于超筋梁。当ξ=ξ_b时，可求出界限破坏时的特定配筋率，即适筋梁的最大配筋率ρ_max值。由图3-13c，取，x=x_b，A_s=ρ_maxbh₀，则

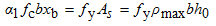                  （3-18）

故 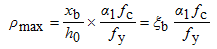                                              （3-19）

   为了方便，将配置具有明显屈服点钢筋的普通钢筋混凝土受弯构件的最大配筋率整理如表3-4。

                                表3-4 受弯构件的最大配筋率ρ_max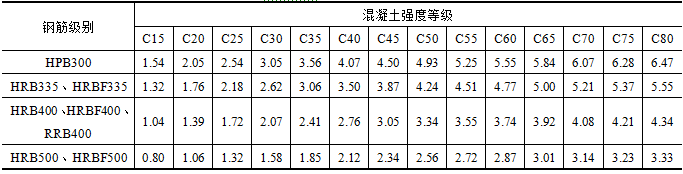（%）               （2）使用无明显屈服点钢筋的受弯构件

对于碳素钢丝、钢绞线、热处理钢筋及冷轧带肋钢筋等无明显屈服点的钢筋，取对应于残余应变为0.002时的名义屈服点应力σ_0.2作为抗拉强度设计值。

根据平截面变形的假设，用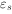代替式（3-17a）中的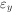，可以求出使用无明显屈服点钢筋的受弯构件的界限相对受压区高度ξ_b的计算式：

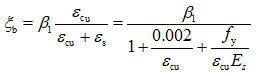                    （3-17b）

5.适筋和少筋破坏的界限条件

为了避免发生少筋破坏形态，必须确定构件的最小配筋率ρ_min。

最小配筋率是少筋梁与适筋梁的界限配筋率。配有最小配筋率ρ_min钢筋混凝土梁的抗弯承载力M_u应等于同样截面、同一强度等级的素混凝土梁的开裂弯矩M_cr。

对素混凝土梁：考虑到混凝土的塑性系数0.9及材料分项系数1.4，开裂弯矩计算公式为

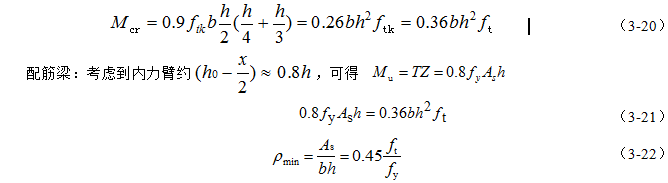
由上式可知，ρ_min与混凝土抗拉强度及钢材强度有关。《规范》在综合考虑温度、收缩应力的影响及以往的设计经验基础上，对最小配筋率ρ_min规定如下：

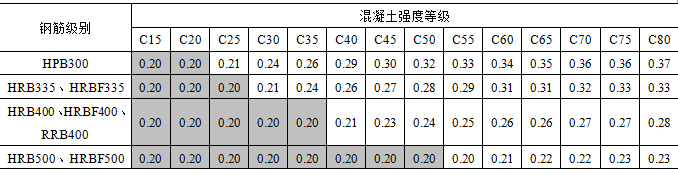
①受弯构件、偏心受拉、轴心受拉构件，其一侧纵向受拉钢筋的配筋率不应小于0.2%和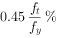中的较大值；据此，不同混凝土强度等级和不同钢筋级别的最小配筋率如表3-5所示，图中灰色区域为0.2%起控制作用的范围。

②卧置与地基上的混凝土板，板的受拉钢筋的最小配筋率可适当降低，但不应小于0.15%。

                                                                           表3-5 受弯构件的最小配筋率ρ_min（%）

                     6.经济配筋率

受弯构件在截面高宽比合适的情况下，可根据材料价格和施工费用可以确定出不同配筋率时的造价，从而得出经济配筋率。实践经验表明，当ρ在最经济配筋率附近波动时，总造价的波动很小。所以，设计时，ρ可在经济配筋率区间取值，板的经济配筋率约为0.3%～0.8%，单筋矩形截面的经济配筋率约为0.6%～1.5%，T形截面的经济配筋率约为0.9%～1.8%。

1. 比照矩形截面的方程，推导圆形截面的正截面承载力计算公式。

2. 确定等效矩形应力图的原则是什么？

       讲一讲深受弯构件的正截面承载力计算方法，这是很多教科书中所不讲的。

3.2.6  深受弯构件的正截面受弯承载力计算

钢筋混凝土受弯构件根据其跨高比的不同，可分为三种类型：

浅梁：l₀/h>5;

短梁： l₀/h=2(2.5)~5；

深梁：l₀/h≦2（简支单跨梁），l₀/h≦2.5（多跨连续梁）。

式中，h为梁截面高度；l₀ 为梁的汁算跨度.可取l_c 和l_n 两者中较小值；l_c 为支座中心线之间的距离；l_n为梁的净跨。

    浅梁在实际工程中应用较多，可称为一般受弯构件。短梁和深梁又称为深受弯构件。深受弯构件的承载力巨大，故而广泛应用于建筑土程、水工、港工、铁路、公路、市政等土木工程中，如双肢柱肩梁、框支剪力墙、剪力墙连梁、梁板式筏形基础反梁、箱形基础箱梁、高层建筑转换层大梁、浅仓侧板、矿井井架大梁以及高桩码头横梁等。

    简支深梁的内力计算与一般梁相同，但连续深梁的内力值及沿跨长的分布规律与一般连续梁不同，其跨中正弯矩比一般连续梁的偏大，而支座负弯矩却偏小，且随跨高比和跨数而变化。因此，在工程设计中，连续深梁的内力应由二维弹性分析确定，且不宜考虑内力重分布，具体计算方法可采用弹性有限元或其他方法。《规范》考虑了相对受压区高度和跨高比的影响，给出了深受弯构件的正截面受弯承载力计算公式

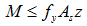                       （3-67）

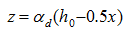                  （3-68）

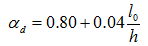                 （3-69）

    当l₀<h时，取内力臂Z=0.6 l₀ 。

式中 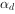——深受弯构件内力臂修正系数；

      x——截面受压区高度，当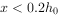时，取