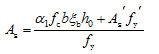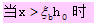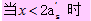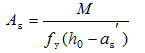3.5双筋矩形截面受弯构件的正截面承载力计算

    大家好！这一讲我们学习双筋矩形截面受弯构件的正截面承载力计算。包括2个知识点：一个是双筋矩形截面承载力计算的基本原理；另一个是工程应用——截面设计和截面复核。

学习要求是：掌握双筋矩形截面正截面承载力计算的基本原理；掌握其工程应用。

3.5.1正截面承载力计算原理

1.双筋矩形截面梁的应用范围

双筋矩形截面受弯构件是指在截面的受拉区和受压区都配有纵向受力钢筋的矩形截面梁。工程上在下列情况下采用双筋梁：

1）弯矩很大，按单筋矩形截面计算所得的x＞x_b，而梁的截面尺寸和混凝土强度等级受到限制，不能提高时；

2）梁在不同荷载组合下（如地震）承受变号弯矩作用时。在结构的抗震设计中，梁端存在变号弯矩，一般将梁端设计成双筋截面，这样既能满足承受变号弯矩的要求，又能提高截面的延性，减少截面开裂和构件变形；

3）在抗震设计中为提高截面的延性或由于构造原因，要求梁必需配置一定比列的纵向钢筋时。

试验表明，双筋矩形截面破坏时的受力特点与单筋矩形截面类似。双筋矩形截面梁与单筋矩形截面梁的区别在于受压区配有纵向受压钢筋，因此只要掌握梁破坏时纵向受压钢筋的受力情况，就可与单筋矩形截面类似建立计算公式。

由于纵向受拉钢筋和受压钢筋数量和相对位置的不同，梁在破坏时它们可能达到屈服，也可能未达到屈服。与单筋矩形截面梁类似，双筋矩形截面梁也应防止脆性破坏，使双筋梁破坏从受拉钢筋屈服开始，故必须满足条件x≤x_b。而梁破坏时受压钢筋应力取决于其应变ε¢_s，由图3-19可知：

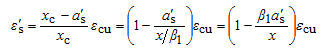            （3-32）

若取a'_s=0.5x，则由平截面假定可得受压钢筋的压应变ε'_s=(1-0.5β₁)ε_cu。当混凝土强度等级为C80时，由ε_cu =0.003 ，β₁=0.74，得：ε'_s=0.00189；其它级别的混凝土对应的ε'_s更大，对于HPB300、HRB335和HRB400级钢筋，其相应的压应力σ'_s已达到抗压强度设计值f '_y。因此双筋矩形截面梁计算中，纵向受压钢筋的抗压强度采用f '_y的必要条件是：

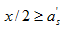                              （3-33）

式中：a'_s——截面受压区边缘到纵向受拉钢筋合力作用点之间的距离。

式（3-33）含义是：受压钢筋位置应不低于矩形应力图中受压区的重心。若不满足上式规定，则表明受压钢筋离中和轴太近，受压钢筋压应变ε'_s过小，致使σ'_s达不到f '_y。

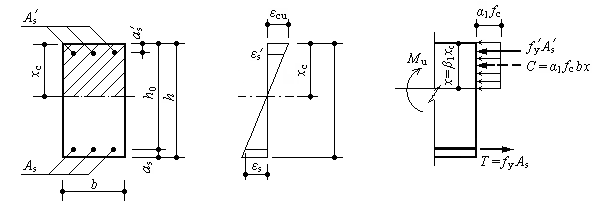
                           图3-19  双筋矩形截面受弯构件正截面承载力计算简图

2.基本公式及适用条件

（1）基本公式

双筋矩形截面受弯构件正截面承载力计算简图如图3-19所示。

根据力的平衡条件可得

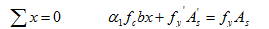                         （3-34）

根据力矩的平衡条件可得

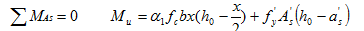              （3-35）

（2）适用条件

应用上述计算公式时，必须满足以下条件：

1）为了防止超筋破坏，保证构件破坏时纵向受拉钢筋首先屈服，应满足

ξ≤ξ_b，或x≤ξ_bh₀，或r≤r_max

2）为了保证受压钢筋在构件破坏时达到屈服强度，应满足x/2≥a'_s。

当条件2）不满足时，受压钢筋应力还未达到f '_y，因应力值未知，精确计算比较复杂。可近似地取x/2=a'_s，并对受压钢筋的合力作用点取矩（图3-20），则正截面承载力可直接根据下式确定：

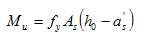                      （3-36）

值得注意的是，按上式求得的A_s可能比不考虑受压钢筋而按单筋矩形截面计算的A_s还小，这时应按单筋矩形截面的计算结果配筋。

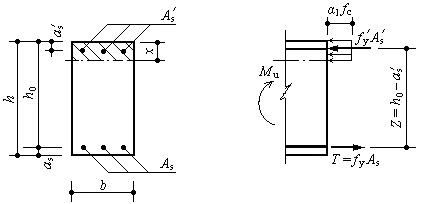
图3-20  x/2<a'_s时双筋矩形截面受弯构件正截面承载力计算简图

3.计算公式的应用

双筋矩形截面受弯构件正截面承载力计算包括截面设计和截面复核两类问题。

（1）截面设计

双筋矩形截面受弯构件的正截面设计，一般是受拉、受压钢筋A_s和A¢_s均未知，都需要确定。有时由于构造等原因，受压钢筋截面面积A¢_s已知，只要求确定受拉钢筋截面面积A_s。截面设计时，令M=M_u，分两种情况讨论。

情形Ⅰ：已知截面的弯矩设计值M、构件截面尺寸b´h、混凝土强度等级和钢筋级别，求受拉钢筋截面面积A_s和受压钢筋截面面积A¢_s。

求解A_s、A¢_s和x三个未知量，只有式（3-34）和（3-35）两个基本计算公式，需补充一个条件才能求解。在截面尺寸和材料强度确定的情况下，当（A_s+A¢_s）最小时最节约钢材。一般情况下，取f_y=f_y¢。

由式（3-35）得

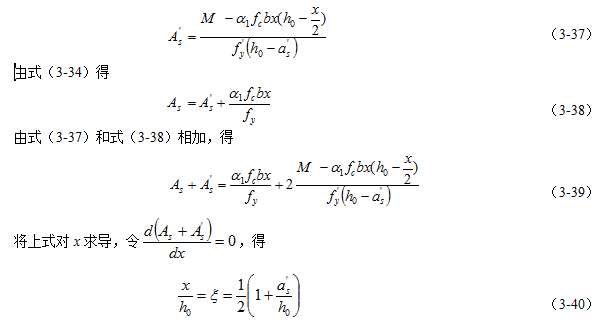
对于HRB335、HRB400级钢筋以及常用的a_s¢/h₀值的情况下，由式（3-40）得x≥x_b，根据适筋公式适用条件，取x=x_b。对于HPB300级钢筋，在混凝土强度等级小于C50时，若仍取x=x_b，则钢筋用量会略有增加，此时可取x=0.55。

当取x=x_b时，则由式（3-35）得

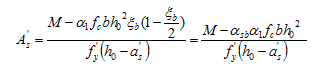             （3-41）

如果 A¢_s≤0，说明不需要配置受压钢筋，可按单筋梁计算受拉钢筋A_s。若A¢_s>0，则由式（3-34）得

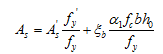                                 （3-42）  

       情形Ⅱ：已知截面的弯矩设计值M、截面尺寸b×h、混凝土强度等级和钢筋级别、受压钢筋截面面积A¢_s，求构件受拉钢筋截面面积A_s。

方程组中只有A_s和x两个未知数，可直接求解。由式（3-35）得

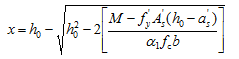          （3-43）

在求出受压区高度x以后，应注意验算适用条件是否满足。

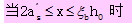，代入式（3-35）得

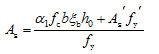                      （3-44）

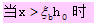，说明给定的A¢_s不足，应加大截面尺寸或按A¢s未知的情况1分别求As及As¢。

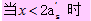，说明As¢过大, 受压钢筋应力达不到f_y¢，式 (3－34), (3－36)已不适用, 应按式（3-45）计算受拉钢筋截面面积A_s。

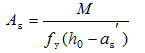                            （3-45）

（2）截面复核

已知截面弯矩设计值M，截面尺寸b×h、混凝土强度等级和钢筋级别，受拉钢筋A_s和受压钢筋A¢_s，复核正截面受弯承载力M_u是否足够。

复核步骤：

由式（3-34）确定x，若x满足适用条件，则代入式（3-35）确定受弯承载力M_u；若x/2＜a¢_s，则按式（3-36）确定M_u；若x＞ξ_bh₀，则取ξ=ξ_b，代入式（3-35）确定M_u；

将截面受弯承载力M_u与截面弯矩设计值M进行比较，若M_u≥M，则说明截面承载力足够，构件安全；反之，若M_u＜M，则说明截面承载力不够，构件不安全，需重新设计，直至满足要求为止。

3.5.2工程应用案例

1. 什么是双筋截面？在什么情况下才采用双筋截面？双筋截面中的受压钢筋和单筋截面中的架立钢筋有何不同？双筋梁中是否还有架立钢筋？

2. 双筋矩形截面受弯构件正截面承载力计算的基本公式及适用条件是什么？为什么要规定适用条件？

3. 双筋矩形截面受弯构件正截面承载力计算为什么要规定x³2a_s’？当x<2a_s’应如何计算？

4. 某框架结构的主梁，截面尺寸为b×h=250mm×600mm，处于一类环境。选用C20混凝土和HRB335级钢筋，承受弯矩设计值M=320kN·m。由于构造等原因，在受压区已经配有2根直径为20的受压钢筋（A¢_s=628mm²），试求所需受拉钢筋面积。

生态混凝土——环保小能手

生态混凝土的原理是通过材料筛选、添加功能性添加剂，采用一种特殊工艺制造出来新型产品。它本身所具备的特殊结构和功能，不仅能够减少环境负荷，更在提高生态环境的协调方面做出了重大贡献。

目前，这种新型混凝土主要适用于边坡治理（包括河流、湖泊、水库堤坝以及道路两侧的边坡治理）等方面。

生态混凝土的优势：

生态混凝土也可以称作“植被混凝土”、“绿化混凝土”等。它不仅能够适应绿色植物的生长，更具有一定的防护功能。作为混凝土界的环保小能手，生态混凝土有着极高的透水性、承载力以及良好的装饰效果，保护了人类赖以生存的自然环境不再遭受破坏。相信今后生态混凝土的发展方向也会在日常生活中逐渐广泛应用开来。
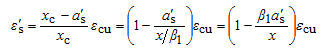
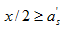
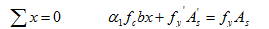
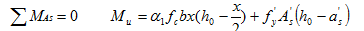
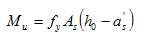
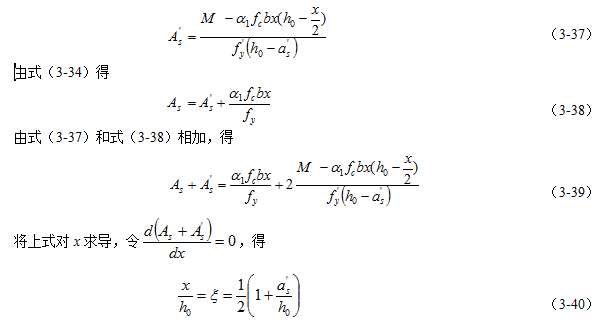
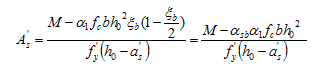
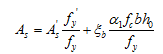
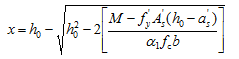
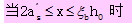