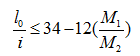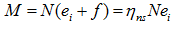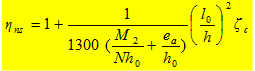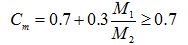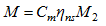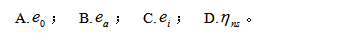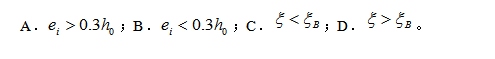5.4二阶弯矩对承载力的影响
钢筋混凝土偏心受压构件在偏心轴向力的作用下将产生弯曲变形,使临界截面的轴向力偏心距增大。图5-19为一两端铰支柱,在其两端作用偏心轴向力,在此偏心轴向力的作用下,柱将产生弯曲变形,在临界截面处将产生最大挠度,因此,临界截面的偏心距由ei增大到ei+f,弯矩由Nei增大到N(ei+f),这种现象称偏心受压构件的纵向弯曲,也称二阶效应。对于长细比小的柱,即所谓“短柱”,由于纵向弯曲很小,一般可以忽略不计;对于长细比大的柱,即所谓“长柱”,纵向弯曲的影响则不能忽略。
钢筋混凝土长柱在纵向弯曲的作用下,可能发生两种形式的破坏。一是“失稳破坏”,二是“材料破坏”。所谓“失稳破坏”是指长细比较大的柱,其纵向弯曲效应随轴向力呈非线性增长,构件发生侧向失稳破坏;“材料破坏”是指破坏时材料达到极限强度。考虑纵向弯曲作用的影响,在同等条件下长柱的承载能力低于短柱的承载能力。
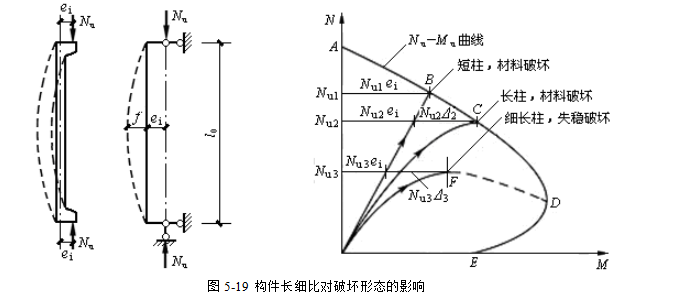 纵向弯曲效应对具有不同长细比的钢筋混凝土柱的影响分析,偏心受压构件的M–N关系曲线见图5-19。当构件为短柱时,纵向弯曲效应可以忽略,偏心距保持不变,截面的弯距与轴力呈线性关系,沿直线达到破坏点,破坏属于“材料破坏”。当构件为长柱时,纵向弯曲效应不能忽略,随着轴力的增大,纵向弯曲引起的偏心距呈非线性增大,截面的弯距也随着偏心距的增大呈非线性增大,如OC线所示。在长细比不是很大的情况下,也发生“材料破坏”于C点;当长细比很大的情况下,纵向弯曲效应非常明显,当轴向力达到一定值时(F点),由于纵向弯曲引起的偏心距急剧增大,微小的轴力增量可引起不收敛的弯矩增量,导致构件侧向失稳破坏。由图可见,在初始偏心距相同的情况下,不同的长细比,偏心受压构件所能承受的极限压力是不同的,长细比越大,纵向弯曲效应越明显,轴力越小。
纵向弯曲效应对具有不同长细比的钢筋混凝土柱的影响分析,偏心受压构件的M–N关系曲线见图5-19。当构件为短柱时,纵向弯曲效应可以忽略,偏心距保持不变,截面的弯距与轴力呈线性关系,沿直线达到破坏点,破坏属于“材料破坏”。当构件为长柱时,纵向弯曲效应不能忽略,随着轴力的增大,纵向弯曲引起的偏心距呈非线性增大,截面的弯距也随着偏心距的增大呈非线性增大,如OC线所示。在长细比不是很大的情况下,也发生“材料破坏”于C点;当长细比很大的情况下,纵向弯曲效应非常明显,当轴向力达到一定值时(F点),由于纵向弯曲引起的偏心距急剧增大,微小的轴力增量可引起不收敛的弯矩增量,导致构件侧向失稳破坏。由图可见,在初始偏心距相同的情况下,不同的长细比,偏心受压构件所能承受的极限压力是不同的,长细比越大,纵向弯曲效应越明显,轴力越小。
因此,在偏心受压构件承载能力分析中不能忽略纵向弯曲的影响,而且要防止发生“失稳破坏”。纵向弯曲影响的实质是临界截面的偏心距和弯矩大于初始偏心距和柱端弯矩。纵向弯曲引起的弯矩称二阶弯矩,其大小与构件两端的弯矩情况和构件的长细比有关。
弯矩作用平面内截面对称的偏心受压构件,当同一主轴方向的杆端弯矩比M1/M2≦0.9、且轴压比不大于0.9时,若构件的长细比满足式(5-12)的要求时可不考虑轴向压力在该方向挠曲杆件中产生的附加弯矩影响,否则应按截面的两个主轴方向分别考虑轴向压力在挠曲杆件中产生的附加弯矩影响。
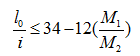 (5-12)
(5-12)
式中M——分别为已考虑侧移影响的偏心受压构件两端截面按弹性分析确定的对同一主轴组合弯矩设计值,绝对值较大端为M2,绝对值较小端为M1,当构件按单曲率弯曲时M1/M2取正值,否则取负值。
l0 ——构件计算长度,可近似取偏心受压构件相应主轴方向上下支撑点之间的距离;
i ——偏心方向的截面回转半径。
1.弯矩增大系数
(1)两端弯矩相等的受压柱
对于两端铰支且两端作用有相等的轴向力,偏心距也相同的偏心受压柱,如图5-20所示。构件在弯矩的作用下,会产生侧向挠度,构件各截面的弯矩随之增大,并产生新的附加侧向挠度。在构件中点的侧向挠度最大,二阶弯矩最大,因此构件的中点截面为临界截面。设计时应将临界截面的内力值做为内力控制值。其弯矩为
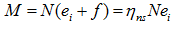 (5-13)
(5-13)
ηns为弯矩增大系数,《规范》给出的计算公式为
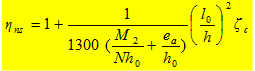 (5-15)
(5-15)
式中:ζc——偏心受压构件的截面曲率修正系数,ζc=0.5fcA/N,当ζc>1.0时取1.0;
l0 ——构件的计算长度,按表5-1或表5-2中有关规定取值;
h ——截面高度,对环形截面取外径d;对圆形截面取直径d;
h0——截面有效高度,对环形截面取h0= r2+ rs;对圆形截面取h0= r+ rs;
r、r2、rs——分别为圆形截面的半径、圆环的外径、钢筋中心所在圆周的半径;
A——受压构件的截面面积,对于T形和I形截面,均取A =bh +2(b'f -b) h'f 。
当偏心受压构件的长细比l0/h≤5或l0/d≤5或l0/i≤17.5时,可不考虑纵向弯曲对偏心距的影响,取ηns=1.0。
(2)两端弯矩不相等的受压柱
构件两端的弯矩不相等但符号相同时,最大挠度不发生在中点,增大后的杆件中部弯曲有可能超过柱端控制截面的弯矩。当两端弯矩M1/M2>0.9时,在该柱两端相同方向、几乎相同大小弯矩作用下将产生最大的偏心距,这时需考虑偏心距调整系数,《规范》规定偏心距调整系数Cm采用下面公式计算:
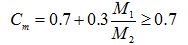 (5-16)
(5-16)
式中 M1 ,M2——分别为已考虑侧移影响的偏心受压构件两端截面按弹性分析确定的对同一主轴组合弯矩设计值,绝对值较大端为M2,绝对值较小端为M1,当构件按单曲率弯曲时取正值,否则取负值。
两端弯矩不相等但符号相反时,构件产生反弯点,纵向弯曲引起的二阶弯矩也有反弯点,因此,二阶弯矩可能并不使构件的最大弯矩发生变化,或仅有较小的增加。为了简化计算,《规范》偏于安全地取式(5-15)作为各类构件通用的弯矩增大系数。
上述分析中没有考虑柱有侧移,而实际的偏心受压柱会发生侧移。有侧移的情况下,偏心受压柱的挠曲线与无侧移柱的不同,二阶弯矩增大,一般在结构整体分析中考虑。
2.柱的计算长度
(1)刚性屋盖的单层房屋排架柱、露天吊车柱和栈桥柱,其计算长度按表5-1采用;
(2)一般多层房屋中的梁柱为刚接的框架结构,各层柱的计算长度按表5-2采用;
(3)当水平荷载产生的弯距设计值占总弯距设计值的75%以上时,框架柱的计算长度可按下列公式计算,取其中的较小值:
l0=[1+ 0.15(ψu+ ψl)]H (5-17(a))
l0=(2+ 0.2ψmin ) H (5-17(b))
式中:ψu、ψl——为柱的上端、下端节点处交汇的各柱线刚度之和与交汇的各梁线刚度之和的比值;
ψmin ——比值ψu、ψl中的较小值;
H——柱的高度,按表5-2采用。
3.柱的控制截面弯矩设计值计算方法
除排架柱结构外的偏心受压构件,在其偏心方向上考虑轴向压力在挠曲杆件中产生的附加弯矩后控制截面的弯矩设计值,按下列公式计算:
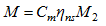 (5-18)
(5-18)
当Cmηns小于1.0时取1.0;对于剪力墙及核心筒,可取Cmηns等于1.0。
1. 偏心受压构件计算中,通过哪个因素来考虑二阶偏心矩的影响( D )。
2. 判别大偏心受压破坏的本质条件是:( C )。
【作业】
1.偏心受压短柱和长柱有何本质的区别?偏心距增大系数的物理意义是什么?
2.附加偏心距ea的物理意义是什么?如何取值?
P-δ与P-Δ效应
编辑删除
混凝土柱计算长度系数与结构二阶效应有着密切的关系,混凝土结构的二阶效应由两部分组成:P-δ效应与P-Δ效应。P-δ效应是指由于构件在轴压力作用下,自身发生挠曲引起的附加效应,可称之为构件挠曲二阶效应;P-Δ效应是指由于结构的水平变形而引起的重力二阶效应,结构发生的水平绝对侧移越大,P-Δ效应越显著,若结构的水平变形过大,则有可能因重力二阶效应而导致结构失稳。
P-δ效应与P-Δ效应具有很强的非线性特征,准确分析现阶段还有困难,主要分析方法有:
1、P-Δ效应计算:
(1)等效几何刚度的有限元法:即由重力二阶效应产生的内力反算出结构的几何刚度,再将其与结构本身的总刚集合,最终形成等效刚度矩阵。
(2)折减弹性抗弯刚度的有限元法:即采用折减的等效刚度,近似的考虑钢筋混凝土结构中各类构件在极限状态时因结构开裂而导致刚度减小现象,使分析结果与设计状态尽可能一致;《混凝土结构设计规范》引入了该方法,第7.3.12条规定,当采用考虑二阶效应的弹性分析方法时,宜在结构分析中对钢筋混凝土构件的弹性抗弯刚度乘以下列折减系数:梁取0.4,柱取0.6,对未开裂的剪力墙和核心筒取0.7,对已开裂的剪力墙和核心筒0.45。
(3)结构位移和构件内力增大系数法:即对不考虑重力二阶效应的分析结果乘以增大系数,近似考虑重力二阶效应。《高规》5.4.2与5.4.3条做了相关规定。
(4)等效水平力的有限元迭代法:根据楼层重力荷载,以及楼层在水平荷载作用下产生的层间位移,计算出考虑效应的近似等效水平荷载向量,然后对结构的有限元方程进行迭代求解,直到迭代结构收敛,得到最终的位移和相应的构件内力。
2、P-δ效应计算:
(1)采用考虑二阶效应的弹性分析方法(即折减弹性抗弯刚度的有限元法),直接计算出结构构件各控制截面的内力设计值;
(2)偏小距增大系数法:短柱可不考虑,长柱则要考虑;
3、程序采用的方法:
目前程序是按照高规的规定执行的,将两种效应分开考虑:P-Δ效应采用等效刚度的有限元近似方法计算;P-δ效应采用偏心距增大系数近似计算。也就是说,无论用户是否选择考虑P-Δ效应,程序总是按规范要求考虑柱长度系数η,计算偏心距增大系数,以保证设计安全,至于是否需要考虑P-Δ效应,则需从计算结果中的刚重比进行计算,需要进行二次计算。