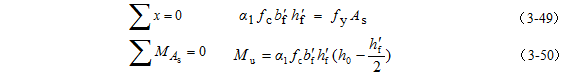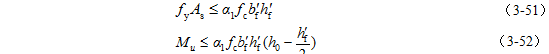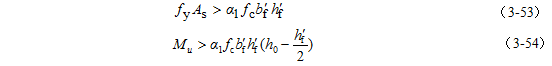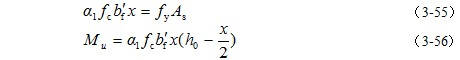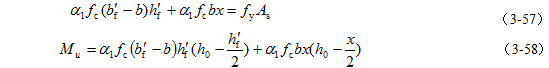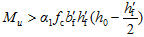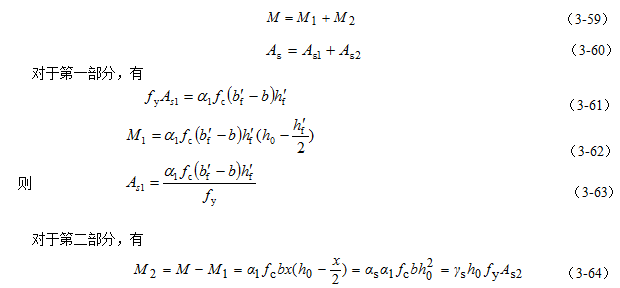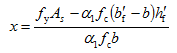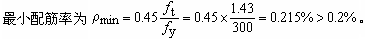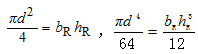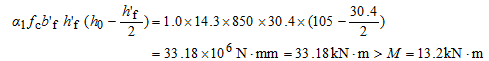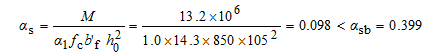3.6  T形截面受弯构件的正截面受弯承载力计算

    大家好！这一讲我们学习T形截面受弯构件的正截面承载力计算。包括2个知识点：一个是T形截面承载力计算的基本原理；另一个是工程应用——截面设计和截面复核。

学习要求是：掌握T形截面正截面承载力计算的基本原理；掌握其工程应用。

3.6.1正截面承载力计算原理

 1. T形截面的由来

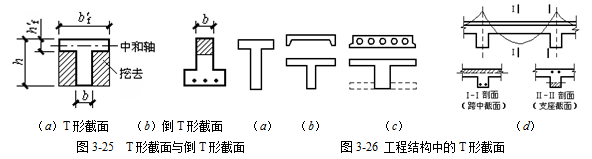
矩形截面受弯构件进入破坏阶段以后，大部分受拉区混凝土已退出工作，对极限承载力的贡献很小。所以，正截面承载力计算时，不考虑混凝土的抗拉强度。既然如此，将矩形截面构件受拉区两侧的部分混凝土去掉，将原有纵向受拉钢筋集中布置在梁肋中，形成T形截面，其极限承载能力不受影响，同时还能节省混凝土，减轻构件自重，产生一定的经济效益。如图3-25所示的T形截面中，伸出部分称为翼缘(b¢_f -b)×h¢_f ，中间部分称为梁肋（b×h）。

T形截面受弯构件广泛应用于工程实际中。例如：①独立T形梁、工字形截面梁，如屋面梁、吊车梁；②现浇肋梁楼盖的梁与楼板浇筑在一起形成T形梁；③槽形板、双T屋面板、薄腹屋面梁以及预制空心板等（图3-26）。如果翼缘在梁的受拉区，则为倒T形截面梁（图3-26b），计算受弯承载力时应按宽度为b的矩形截面计算。现浇肋梁楼盖连续梁的支座附近截面就是倒T形截面（图3-26d），该处承受负弯矩，使截面下部受压（II-II剖面），翼缘（上部）受拉，而跨中（I-I剖面）则按T形截面计算。

2.T形截面的翼缘计算宽度

T形截面翼缘参与受压。试验研究与理论分析证明，翼缘的压应力分布不均匀，离梁肋越远应力越小（图3-27a、c），可见翼缘参与受压的有效宽度是有限的。为简化计算，在设计T形截面梁时应将翼缘限制在一定范围内，并假定混凝土的压应力在b¢_f范围内均匀分布，这个宽度称为翼缘的计算宽度b¢_f。

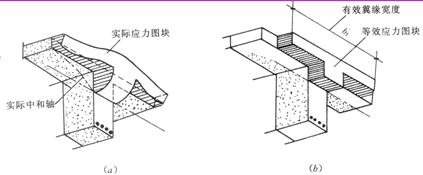
图3-27   T形截面应力分布图 

《规范》规定了T形及倒L形截面受弯构件翼缘计算宽度b¢_f的取值，考虑到b¢_f与翼缘厚度、梁跨度和受力状况等因素有关，应按表3-8中规定各项的最小值采用。 

                        表3-8  T形和倒L形截面受弯构件翼缘计算宽度b¢_f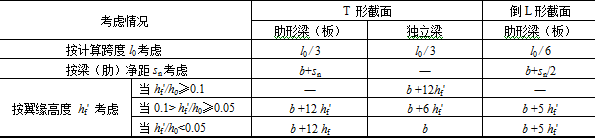                                      

3.基本公式及适用条件

1）T形截面的两种类型及判别条件

T形截面受弯构件正截面受力的分析方法与矩形截面的基本相同，不同之处在于需要考虑受压翼缘的作用。根据中和轴是否在翼缘内，将T形截面分为以下两种类型：

①第一类T形截面：中和轴在翼缘内，即x≤h_f'；

②第二类T形截面：中和轴在梁肋内，即x＞h_f'。

要判断中和轴是否在翼缘中，首先应对中和轴在翼缘与梁肋交界处，即x=h_f' 处的界限情况进行分析（图3-29）。

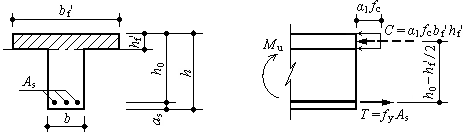
图3-29   x=h_f'时的T形截面

 根据力的平衡条件

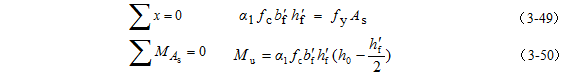
对于第一类T形截面，有x≤h_f'，则

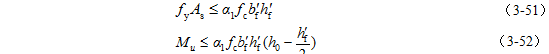
对于第二类T形截面，有x＞h_f'，则

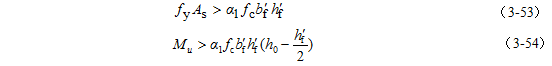
以上即为T形截面受弯构件类型判别条件。但应注意不同设计阶段采用不同的判别条件：

1）在截面设计时，由于A_s未知，采用式（3-52）和式（3-54）进行判别；

2）在截面复核时，A_s已知，采用式（3-51）和式（3-53）进行判别。

2、第一类T形截面承载力的计算公式

由于不考虑受拉区混凝土的作用，其承载力主要取决于受压区的混凝土，故第一类T形截面的承载力与梁宽为b_f' 矩形截面完全相同，计算公式为

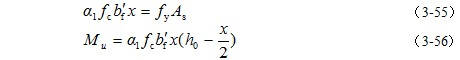
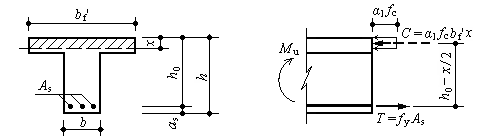
图3-30  第一类T形截面

适用条件：

1）x≤ξ_bh₀。由于T形截面的h_f' 较小，而第一类T形截面中和轴在翼缘中，故x值较小，该条件一般都可满足，不必验算。

2）A_s≥ρ_minbh。应该注意的是，最小配筋面积按ρ_minbh而不是ρ_minb_f'h。

对于工字形截面和倒T形截面，应满足A_s≥ρ_min[bh+(b_f -b)h_f]

3、第二类T形截面承载力的计算公式

第二类T形截面的中和轴在梁肋中，可将该截面分为伸出翼缘和矩形梁肋两部分，如图3-31所示，则计算公式根据平衡条件得

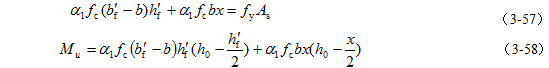
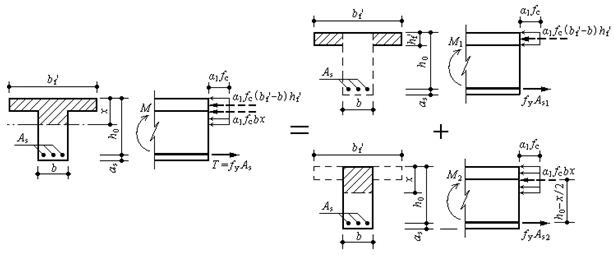
图3-31  第二类T形截面

适用条件：

1）x≤ξ_bh₀；

2）A_s≥ρ_min[bh+(b_f -b)h_f]。该条件一般都可满足，不必验算。

3.6.3.计算公式的工程应用

（1）截面设计

已知：截面弯矩设计值M、截面尺寸、混凝土强度等级和钢筋级别，求受拉钢筋截面面积A_s。

设计步骤：

首先判别截面类型，按相应的公式计算，最后验算适用条件。

当满足时，为第一类T形截面，按梁宽为b_f'的单筋矩形截面计算。

当满足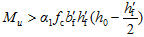时，为第二类T形截面，根据式（3-57）和式（3-58）计算。若将翼缘伸出部分视作双筋矩形截面中的受压钢筋，可以看出第二类T形截面与双筋矩形截面相似（图3-31），因此也可按双筋矩形截面计算方法分析，有

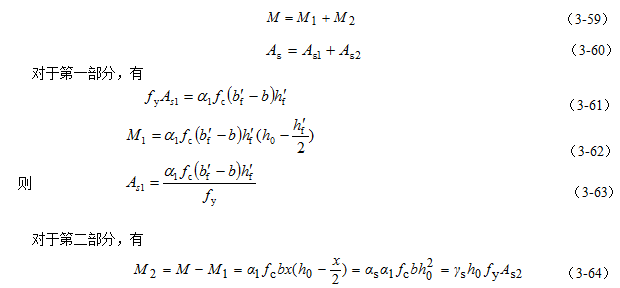
与梁宽为b的单筋矩形截面一样，根据式（3-64）确定α_s，查表3-8得相应的γ_s，则

                                                               （3-65）

验算x≤ξ_bh₀。

（2）截面复核

已知：截面弯矩设计值M，截面尺寸、受拉钢筋截面面积A_s、混凝土强度等级及钢筋级别，求

正截面受弯承载力M_u是否足够。

复核步骤：

首先判别截面类型，根据类型的不同，选择相应的公式计算，最后验算适用条件。

当满足式（3-51）时，为第一类T形截面，按b_f'×h的单筋矩形截面受弯构件复核方法进行；当

满足式（3-53）时，为第二类T形截面，有

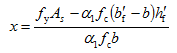                         （3-66）

验算适用条件：若x≤ξ_bh₀，则将x代入式（3-56）得M_u；若x＞ξ_bh₀，则令x=ξ_bh₀计算。若M_u≥M，则承载力足够，截面安全。

3.6.2工程应用案例

【实例3-7】已知预制空心楼板如图3-32a所示。选用C30混凝土和HRB335级钢筋，承受弯矩设计值M=13.2kN·m。试计算所需配置的纵向受力钢筋。

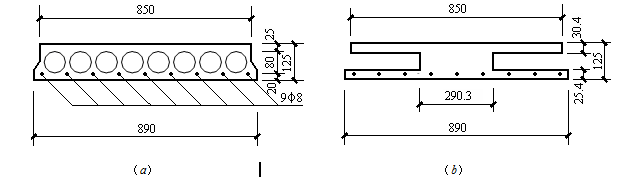
图3-32  【例3-7】图

【解】本例题属于截面设计类。

（1）设计参数 

查附表1-2和1-6及表3-2～3-7可知，C30混凝土f_c=14.3N/mm²，f_t=1.43N/mm²；HRB335级钢筋f_y=300N/mm²；α₁=1.0，α_sb=0.399，ξ_b=0.55；

查附表3-2，一类环境，c=15mm，则a_s=c+d/2=20mm，h₀=h–20=105mm；

（2）将圆孔空心板换算为工字形截面

根据截面面积不变、截面惯性矩不变的原则，先将圆形孔转换为矩形孔。取圆孔直径为d，换算后矩形孔宽为b_R、高为h_R，则

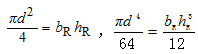
换算后工字形截面尺寸如图3-32b所示。

（3）计算钢筋截面面积

1）截面类型判别

当x=h'_f时

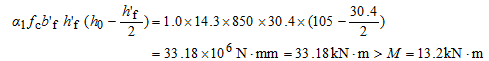
因此，属于第一类截面类型，可以按矩形截面b'_f×h=850mm×125mm计算。

2）求受拉钢筋的面积A_s

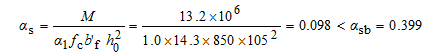
查表3-8，γ_s=0.948，则

符合适用条件。

（4）选配钢筋及绘配筋图

受拉钢筋选用9B8(A_s=453mm²)，配筋简图如图3-32a所示。

【例3-8】已知T形截面梁，截面尺寸和配筋如图3-34所示。选用C25混凝土，试求该截面所能承受的最大弯矩。

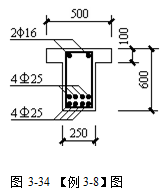
【解】本例题属于截面复核类。

（1）设计参数

查附表1-2和1-6及表3-2～3-7可知，C25混凝土f_c=11.9N/mm²；HRB335级钢筋f_y=300N/mm²；α₁=1.0，α_sb=0.399，ξ_b=0.550；

查附表3-2，一类环境，c=20mm，则a_s=c+d_sv+d+e/2=20+8+25+25/2=65.5mm，取值65mm，h₀=h–65=535mm；a′_s=c+d_sv+d/2=20+8+16/2=36mm，取a′_s=35mm。

A_s=3927mm²，A'_s=402mm²。

（2）截面类型判别

1.第二类T形截面受弯构件正截面承载力计算的基本公式及适用条件是什么？为什么要规定适用条件？

一、相关学习平台

1.中国建筑结构网:

http://www.buildingstructure.com.cn/

2. 混凝土结构设计论坛：

http://bbs.co188.com/forum-170-1.html

3.常用结构小软件

http://xman.six168.com/index.php

二、相关制度法规

1.建筑标准分享网

http://www.bzfxw.com/soft/sort025/1.html

2.混凝土结构设计规范GB 50010-2010

http://www.bzfxw.com/soft/sort025/sort035/35172338.html

三、相关教材阅读

1.《混凝土结构》（第五版）上册：混凝土结构设计原理，东南大学、天津大学、同济大学三校合编，中国建筑工业出版社，2012.8；

2.《混凝土结构设计原理》（第四版），沈蒲生主编， 高等教育出版社，2012.2；

3.混凝土结构设计规范（GB 50010-2010），中华人民共和国住房和城乡建设部主编，中国建筑工业出版社，2011年。