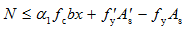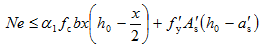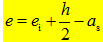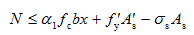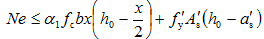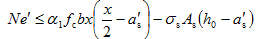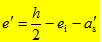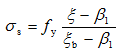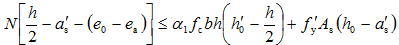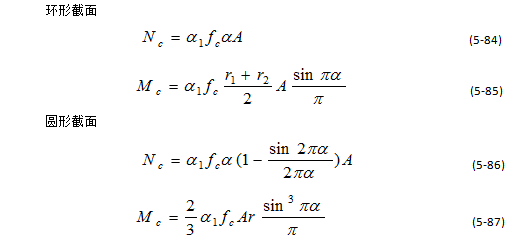5.5偏心受压构件正截面承载力的计算原理

矩形截面偏心受压构件正截面承载力计算采用与受弯构件正截面承载力计算相同的基本假定，用等效矩形应力图形代替混凝土压区的实际应力图形。

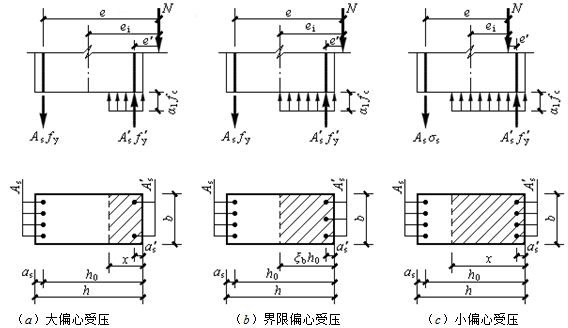
图5-23 矩形截面偏心受压构件正截面承载能力计算图式

1.大偏心受压构件

承载能力极限状态时，大偏心受压构件中的受拉和受压钢筋应力都能达到屈服强度，根据截面力和力矩的平衡条件（图5-23a），大偏心受压构件正截面承载能力计算的基本公式为

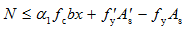                  （5-19）

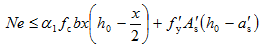      （5-20）

式（5-20）为向远离轴向力一侧钢筋（受拉钢筋）取矩的平衡条件，e为轴向力至受拉钢筋合力点的距离，按下式计算：

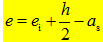                       （5-21）

为了保证受压钢筋A_s' 应力到达f_y' 及受拉钢筋A_s应力达到f_y，构件截面的相对受压区高度应符合下列条件：

2a_s' ≤x≤ξ_bh₀                           （5-22）

2.小偏心受压构件

根据截面力和力矩的平衡条件（图5-23（c）），可得矩形截面小偏心受压构件正截面承载能力计算的基本公式为

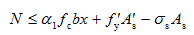                 （5-24）

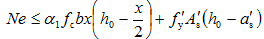        （5-25）

或 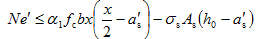                             （5-26）

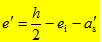                              （5-27）

式中：e'——轴力到受压钢筋合力点之间的距离；

σ_s——远离轴向力一侧钢筋的应力。理论上可按应变的平截面假定求出，但计算过于复杂。可按下式近似计算：

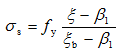                    （5-28）

按上式算得的钢筋应力应符合下列条件：

-f _y' ≤σ_s≤f _y                          （5-29）

当ξ≥2β₁-ξ_b时，取σ_s= -f _y'。当相对偏心距很小且A_s′ 比A_s大得很多时，也可能在离轴向力较远的一侧的混凝土先被压坏，称为反向破坏。为了避免发生反向压坏，对于小偏心受压构件除按式（5-24）和式（5-25）或式（5-26）计算外，还应满足下述条件：

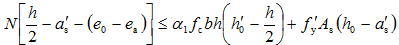 （5-30）

1.试画出矩形截面大偏心受压构件的受力简图,列出承载力计算方程式。

2. 试画出矩形截面小偏心受压构件的受力简图,列出承载力计算方程式。

 【作业】

1. 试推导矩形截面小偏心受压构件中远离轴向力一侧钢筋的应力σ_s的表达式。

知识拓展-环形和圆形截面偏心受压构件正截面承载力计算

土木工程中许多构筑物采用环形或圆形截面。管柱、烟囱、塔身、电线杆、桩、支柱等。环形或圆形截面偏心受压构件正截面承载力计算的基本假定和基本原理与矩形截面偏心受压构件基本相同。

当环形截面受到偏心压力作用时，中性轴一般已进入截面的空心部分，其受压区面积类似于T 形截面的翼缘，如图5-38(a)所示。当受压区高度很小时，混凝土应力图形强度的取值对截面承载力的影响很小。当圆形截面受到偏心压力作用时，受压区面积为弓形，理论上其等效矩形应力图形的强度将低于截面宽度不变的矩形截面情况。为简化计算，《规范》均取等效矩形应力图形的应力值与矩形及T 形截面相同，仍取为。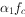

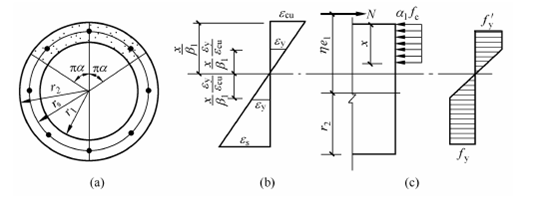
图5-38 环形截面偏心受压构件

当纵向钢筋的根数不少于6 根时，一般纵向受力钢筋均沿周边均匀配置，为计算方便起见一般将纵向钢筋的总面积换算为面积为A_s、半径为r_s的钢环。

1. 混凝土受压区面积A_c

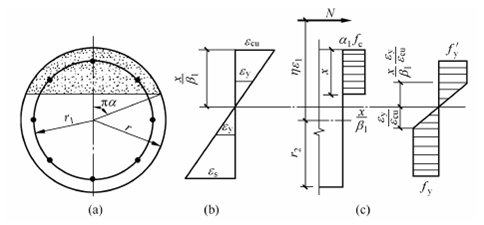
图5-39 圆形截面偏心受压构件

2. 基本公式

当构件受到偏心压力作用时，受压区混凝土受到的合力N_c及其对截面中心的力矩M_c为：

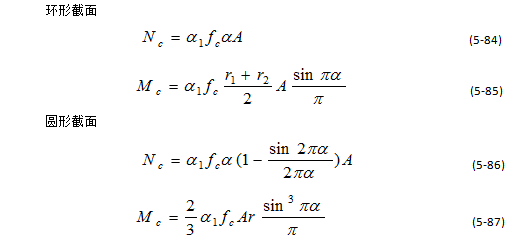
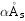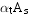钢环中应力一般存在有矩形分布的塑性区及三角形分布的弹性区(如图5-38(c)及图5-39(c)所示)。为了简化计算，可将受压区及受拉区钢环的梯形应力分布近似地简化为应力值为f_y’和f_y的等效矩形应力分布。等效矩形应力分布的受压区及受拉区钢环面积分别为及。经简化后，可导出钢环承担的轴力N_s及其对截面中心力矩M_s为：

 基本公式(5-90)～式(5-93)可用于进行截面承载力的复核，但用于计算截面的纵向配筋面积将出现超越方程，异常复杂，需用迭代方法求解，不便于设计应用。为此可利用一些实用设计手册的计算图表进行设计。