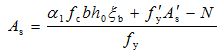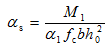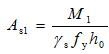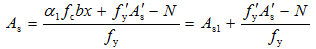5.6不对称配筋偏心受压构件的正截面承载力计算

1.截面设计

（1）偏心受压类别的初步判别

判别两种偏心受压类别的基本条件是：ξ≤ξ_b为大偏心受压；ξ＞ξ_b为小偏心受压。但在截面配筋计算时， A_s′ 和A_s为未知，受压区高度ξ也未知，因此也就不能利用ξ来判别。  

工程设计时，可近似按下面的方法进行初步判别：

当e_i≤0.3h₀时，为小偏心受压；

当e_i＞0.3h₀时，可先按大偏心受压计算。

（2）大偏心受压构件的配筋计算

情形I：受压钢筋A_s′ 及受拉钢筋A_s均未知

两个基本公式（5-19）及式（5-20）中有三个未知数：A_s′、A_s及x，故不能得出唯一解。为了使总的截面配筋面积（A_s+ A_s′）最小，和双筋受弯构件一样，可取x=ξ_bh₀，则由式（5-20）可得：

           （5-31）

按式（5-31）算得A_s′ 应不小于ρ'_minbh，否则可取A_s′=ρ'_minbh，按A_s′为已知的情况计算。将式（5-31）求出的A_s′ 代入式（5-19）可得：

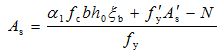              （5-32）

按上式求出的A_s应不小于ρ_minbh。

情形II：受压钢筋A_s′ 为已知，求A_s

当A_s′ 为已知时，式（5-19）及式（5-20）中有两个未知数A_s及x可求得唯一解。由式（5-20）可知Ne有两部分组成：M'= f _y' A_s′(h₀- a_s')及M₁= Ne -M'=α₁ f_c bx(h₀-x/2)。

M₁为压区混凝土与对应的部分受拉钢筋A_s1所组成的力矩。与单筋矩形受弯截面构件相似，有

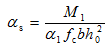                 （5-33）

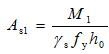                  （5-34）

将A_s′ 及A_s1代入式（5-20）中可写出总的受拉钢筋面积A_s的计算公式：

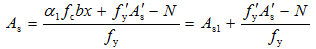 （5-35）

应该指出的是，如果α_s≥α_smax，则说明已知的A_s′ 尚不足，需按A_s′ 为未知的情况重新计算。如果x＜2a'_s，可近似取x=2a'_s，对A_s′ 的合力中心取矩，可求得

               （5-36）

（3）小偏心受压构件的配筋计算

由小偏心受压承载能力计算的基本公式可知，有两个基本方程，但要求三个未知数：A_s′、A_s和x，因此，仅根据平衡条件也不能求出唯一解，需要补充一个使钢筋的总用量最小的条件求ξ。但对于小偏心受压构件要找到与经济配筋相对应的ξ值需用试算逼近法求得，计算较为复杂。小偏心受压应满足ξ＞ξ_b和-f _y'≤σ_s≤f _y两个条件。当纵筋A_s的应力达到受压屈服时（σ_s = -f _y'），由式（5-28）可求得此时的受压区高度为

ξ_cy=2β₁-ξ_b                            （5-37）

当ξ_b＜ξ＜ξ_cy时，A_s不屈服，为了使用钢量最小，可按最小配筋率配置A_s，取A_s=ρ_minbh。因此，小偏心受压配筋计算可采用如下近似方法：

①首先假定A_s=ρ_minbh，并将A_s值代入基本公式中求ξ和σ_s。若σ_s为负值，说明钢筋处于受压状态，取A_s=ρ'_minbh重新代入基本公式中求ξ和σ_s。若满足ξ_b＜ξ＜ξ_cy的条件，则直接利用式（5-25）求出A_s′；

②如果h/h₀＞ξ≥ξ_cy，说明A_s钢筋已屈服，取σ_s = -f _y'，利用小偏压基本公式求A_s′ 和A_s。并验算反向破坏的截面承载能力；

③如果ξ≥h/h₀，取ξ=h/h₀和σ_s= -f _y'，利用小偏压基本公式求A_s′ 和A_s。并验算反向破坏的截面承载能力。

按上述方法计算的A_s应满足最小配筋率的要求。

2.截面承载力复核

当构件截面尺寸、配筋面积A_s及A_s′，材料强度及计算长度均已知，要求根据给定的轴力设计值N（或偏心距e₀）确定构件所能承受的弯矩设计值M（或轴向力N）时，属于截面承载力复核问题。一般情况下，单向偏心受压构件应进行两个平面内的承载力计算，即弯矩作用平面内的承载力计算及垂直于弯矩作用平面内的承载力计算。

（1）给定轴向力设计值N，求弯矩设计值M或偏心距e₀

由于截面尺寸、配筋及材料强度均为已知，故可首先按式（5-23）算得界限轴向力N_b。如满足N≤N_b的条件，则为大偏心受压的情况，可按大偏心受压正截面承载能力计算的基本公式求x和e，由求出的x和弯矩增大η_ns，根据公式（5-21）求出偏心距e₀，最后求出弯距设计值M=Ne₀。

如N＞N_b，则为小偏心受压情况，可按小偏心受压正截面承载能力计算的基本公式求x和e，采取与大偏心受压构件同样的步骤求弯距设计值M=Ne₀。

（2）给定偏心距e₀，求轴向力设计值N

根据e₀先求初始偏心距e_i。当e_i≥0.3h₀时，可按大偏心受压情况，求ζ_c和弯矩增大系数η_ns，再将e_i和η_ns代入公式（5-21）中求e。求出e后，将给定的截面尺寸、材料强度、配筋面积和e等参数代入基本公式，求解x和N，并验算大偏心受压的条件是否满足。如满足x≤ξ_bh₀，为大偏心受压，计算的N即为截面的设计轴力；若不满足，则按小偏心的情况计算。

当e_i＜0.3h₀时，则属小偏心受压，将已知数据代入小偏心受压基本公式中求解x及N。当求得N≤α₁ f_c bh时，所求得的N即为构件的承载力；当N＞α₁ f_c bh时，尚需按式（5-20）求不发生反向压坏的轴向力N，并取较小的值作为构件的正截面承载能力。

（3）垂直弯矩作用平面的承载力计算

当构件在垂直于弯矩作用平面内的长细比较大时，除了验算弯矩作用平面的承载能力外，还应按轴心受压构件验算垂直于弯矩作用平面内的受压承载力。这时应取截面高度b计算稳定系数φ，按轴心受压构件的基本公式计算承载力N。无论截面设计还是截面校核，都应进行此项验算。

1.怎样进行不对称配筋矩形截面偏心受压构件正截面受压承载力的设计与复核？

2. 某矩形截面偏心受压构件的截面尺寸为400×500mm，处于一类环境，柱的计算长度为3.6m，选用C30混凝土和HRB400级钢筋，承受轴力设计值为N=380kN，弯矩设计值为M₁=M₂=230kN·m。求该柱的截面配筋A_s和A_s′。

1.试画出矩形截面大偏心受压构件的受力简图,列出承载力计算方程式。

2.试画出矩形截面小偏心受压构件的受力简图,列出承载

3.某矩形截面偏心受压构件的截面尺寸为400×500mm，处于一类环境，柱的计算长度为3.6m，选用C30混凝土和HRB400级钢筋，承受轴力设计值为N=380kN，弯矩设计值为M₁=M₂=230kN·m。求该柱的截面配筋A_s和A_s′。

4.已知一偏心受压构件，处于一类环境，截面尺寸为500×500mm，柱的计算长度为4.5m，选用C35混凝土和HRB400级钢筋，承受轴力设计值为N=1200kN，A_s=1256mm²， A_s′=1016mm²，求该柱能承受的弯矩设计值。

吸音混凝土——隔绝噪音的有力武器

吸音混凝土顾名思义就是一种可以针对外部产生的噪音采取隔音或者吸音的物质。它具有连续、多孔的内部结构。与普通的密实混凝土不同的是，这种新型混凝土能够直接的面对噪音源。

吸音混凝土的优势：

吸音混凝土的开发就是为了减少交通噪音，同时，它也适应于机场、高速公路、高速铁路两侧，地铁等易产生噪音的一些公共场所，它不仅能够明显地减低交通噪音，更能改善出行环境以及公共交通设施周围的居住环境。