一、直方图(Histogram)
直方图(Histogram)又称频数直方图,由一系列宽度相等、长度不等的长方形来展示特征的频数情况。长方形的宽度表示组距(数据范围的间隔),长度表示在给定间隔内的频数(或频率)与组距的比值,以长方形的面积来表示频数(或频率)。由于分组数据具有连续性,直方图的长方形通常是连续排列的。直方图可以比较直观地展现特征内部数据,便于分析其分布情况。
#例 垂直柱状图 df.plot.bar

#例 叠加柱状图 stacked=True

#例: 水平叠加柱状图 df.plot.barh

#示例 柱状图
import matplotlib.pyplot as plt
import numpy as np
n = 12
X = np.arange(n)
Y1 = (1 - X/float(n)) * np.random.uniform(0.5,1.0,n)
Y2 = (1 - X/float(n)) * np.random.uniform(0.5,1.0,n)
#facecolor:表面的颜色;edgecolor:边框的颜色
plt.bar(X,+Y1,facecolor = '#9999ff',edgecolor = 'white')
plt.bar(X,-Y2,facecolor = '#ff9999',edgecolor = 'white')
#描绘text在图表上
# plt.text(0 + 0.4, 0 + 0.05,"huhu")
for x,y in zip(X,Y1):
#ha : horizontal alignment
#va : vertical alignment
plt.text(x + 0.01,y+0.05,'%.2f'%y,ha = 'center',va='bottom')
for x,y in zip(X,Y2):
# ha : horizontal alignment
# va : vertical alignment
plt.text(x+0.01,-y-0.05,'%.2f'%(-y),ha='center',va='top')
plt.xlim(-.5,n)
plt.yticks([])
plt.ylim(-1.25,1.25)
plt.yticks([])
plt.show()
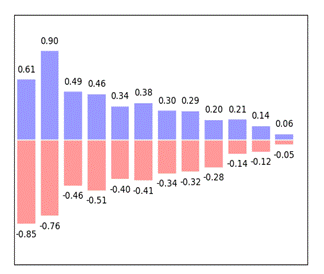
柱状图
二、条形图(Bar Chart)
条形图(Bar Chart)也是由一系列宽度相等、高度不等的长方形来展示特征的频数情况。但条形图主要展示分类数据,一个长方形代表特征的一个类别,长度代表该类别的频数,宽度没有数学意义。相较于面积,肉眼对于高度要敏感许多,故能很好显示数据间的差距。条形图不同类别之间是有空隙的。
三、饼图(Pie Graph)
饼图(Pie Graph)用于表示不同类别的占比情况,通过弧度大小来对比各种类别。饼图通过将一个圆饼按照类别的占比划分成多个区块,整个圆饼代表数据的总量,每个区块(圆弧)表示该分类占总体的比例大小。饼图可以比较清楚地反映出部分与部分、部分与整体之间的比例关系,易于每个类别相对于总数的大小。但因为对于面积大小的不敏感,某些情况下效果不是很好。

四、箱线图
箱线图的上边缘为最大值,下边缘为最小值,但范围不超过盒型各端加1.5倍IQR(四分位距,即上四分位数与下四分位数的极差)的距离。超出上下边缘的值即视为异常值。
如下灰色框里的就是箱形图(英文:Box plot):又称为盒须图、盒式图、盒状图或箱线图,是一种用作显示一组数据分散情况资料的统计图。因型状如箱子而得名。
箱形图最大的优点就是不受异常值的影响,可以以一种相对稳定的方式描述数据的离散分布情况。
五数概括法:即用下面的五个数来概括数据(最小值;第1四分位数(Q1);中位数(Q2);第3四分位数(Q3);最大值),箱形图与之类似。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = [1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000, 2100]
df = pd.DataFrame(data)
df.plot.box(title="hua tu")
plt.grid(linestyle="--", alpha=0.3)
plt.show()

五数概括法:描述数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = [1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000, 2100]
df = pd.DataFrame(data)
print(df.describe())
data = [1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000, 2100]
df = pd.DataFrame(data)
print(df.describe())
df.plot.box(title="hua tu")
plt.grid(linestyle="--", alpha=0.3)
plt.show()
'''输出结果:
count 10.000000 # 条数
mean 1650.000000 # 均值
std 302.765035 # 标准差
min 1200.000000 # 最小值
25% 1425.000000 # 下四分位
50% 1650.000000 # 中位数
75% 1875.000000 # 上四分位
max 2100.000000 # 最大值
'''
价值
1 直观明了地识别数据批中的异常值 箱线图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的耐抗性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不会影响箱形图的数据形状,箱线图识别异常值的结果比较客观。由此可见,箱线图在识别异常值方面有一定的优越性。
2 利用箱线图判断数据批的偏态和尾重
对于标准正态分布的样本,只有极少值为异常值。异常值越多说明尾部越重,自由度越小(即自由变动的量的个数);
而偏态表示偏离程度,异常值集中在较小值一侧,则分布呈左偏态;异常值集中在较大值一侧,则分布呈右偏态。
3 利用箱线图比较几批数据的形状
同一数轴上,几批数据的箱线图并行排列,几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。如上图,可直观得看出第三季度各分公司的销售额大体都在下降。
局限性:不能精确地衡量数据分布的偏态和尾重程度;对于批量比较大的数据,反映的信息更加模糊以及用中位数代表总体评价水平有一定的局限性


