实变函数与泛函分析

张祖锦

目录

  • 2025版
    • ● 简明课件
    • ● 上课视频
  • 作业
    • ● 2020-2021-1作业及讲解
  • 0课程简介
    • ● 0.1自我介绍 Introduction
    • ● 0.2回忆 Riemann 积分-数学分析
    • ● 0.3构造 Lebesgue 积分-实变函数
    • ● 0.4学习实变函数与泛函分析的重要意义
    • ● 0.5实变函数与泛函分析的考核标准与学习方法
    • ● Lebesgue传记
  • 1集合
    • ● 1.1集合的表示
    • ● 1.2集合的运算
      • ● 1.2.1集族
      • ● 1.2.2并集 (union)
      • ● 1.2.3交集 (intersection)
      • ● 1.2.4交并运算律、De Morgan 律及其他
      • ● 1.2.5数学语言的集合表示
      • ● 1.2.6上、下极限集
      • ● 1.2.7单调集列
      • ● 1.2.8集合的直积 (Cartesian product)
    • ● 1.3对等与基数
      • ● 1.3.1对等的定义
      • ● 1.3.2对等的例子
      • ● 1.3.3对等的性质
      • ● 1.3.4基数的比较
    • ● 1.4可数集合
      • ● 1.4.1定义与初步例子
      • ● 1.4.2可数集的性质
      • ● 1.4.3进一步的例子
    • ● 1.5不可数集合 (uncountable set)
      • ● 1.5.1定义与例子
      • ● 1.5.2连续基数的性质
      • ● 1.5.3无最大基数定理
    • ● 本章小结
  • 2点集
    • ● 2.1度量空间, n 维欧氏空间
      • ● 2.1.1度量空间的定义与例子
      • ● 2.1.2邻域、极限及其它
    • ● 2.2聚点, 内点, 界点
      • ● 2.2.1点与集的第一类关系: 内点, 外点, 聚点
      • ● 2.2.2点与集的第二类关系: 聚点, 孤立点和外点
      • ● 2.2.3边界点要么是聚点, 要么是孤立点
      • ● 2.2.4聚点的等价刻画
      • ● 2.2.5闭包的等价刻画
      • ● 2.2.6边界与闭包的关系
      • ● 2.2.7闭包、开核的对偶关系
      • ● 2.2.8开核, 导集, 闭包保持集合的包含关系
      • ● 2.2.9导集与并运算可交换
      • ● 2.2.10导集, 边界不空的充分条件
    • ● 2.3开集, 闭集, 完备集
      • ● 2.3.1开集及其性质
      • ● 2.3.2闭集及其性质
      • ● 2.3.3开集、闭集的对偶性
      • ● 2.3.4紧集、自密集、完备集
    • ● 2.4直线上的开集, 闭集及完备集的构造
      • ● 2.4.1直线上的开集、闭集的构造
      • ● 2.4.2直线上完备集的构造
    • ● 2.5康托尔三分集
      • ● 2.5.1Cantor 三分集的构造
      • ● 2.5.2Cantor 三分集的性质
      • ● 2.5.3维数观点看 Cantor 集
    • ● 本章小结
  • 3测度论
    • ● 引言
    • ● 外测度 (outer measure)
    • ● 3.2可测集 (measurable set)
      • ● 3.2.1可测集的等价定义
      • ● 3.2.2可测集的性质1: 可测集的补, 可测集列的交与并
      • ● 3.2.3可测集的性质2: 可测集列的极限
    • ● 3.3可测集类
      • ● 3.3.1可测集的例子
      • ● 3.3.2可测集的构造
      • ● 3.3.3测度的内、外正规性
    • ● 本章小结
  • 4可测函数
    • ● 引言
    • ● 4.1可测函数及其性质
      • ● 4.1.1记号 (notations)
      • ● 4.1.2可测函数的定义及等价刻画
      • ● 4.1.3重要的可测函数类 I---连续函数类
      • ● 4.1.4重要的可测函数类 II---简单函数类
      • ● 4.1.5可测函数的四则运算
      • ● 4.1.6可测函数的极限运算
      • ● 4.1.7可测函数与简单函数的关系
      • ● 4.1.8几乎处处成立的内涵
    • ● 4.2叶戈罗夫定理
      • ● 4.2.1引言
      • ● 4.2.1Egrov 定理
      • ● 4.2.3Egrov 定理的推广
    • ● 4.3可测函数的构造
      • ● 4.3.1Lusin 定理
      • ● 4.3.2Lusin 定理的另一形式
      • ● 4.3.3可测集与可测函数的总结
    • ● 4.4依测度收敛
      • ● 4.4.1依测度收敛的定义
      • ● 4.4.2依测度收敛不能蕴含几乎处处收敛
      • ● 4.4.3几乎处处收敛不能蕴含依测度收敛
      • ● 4.4.4Riesz 定理 (依测度收敛函数列有一个子列几乎处处收敛)
      • ● 4.4.5Lebesgue 定理 (测度有限时, 几乎处处收敛蕴含依测度收敛)
      • ● 4.4.6依测度收敛的极限的唯一性 (在几乎处处意义下)
      • ● 4.4.7各种收敛态的关系总结
      • ● 4.4.8Riesz 定理的强化版本
    • ● 本章小结
  • 5积分论
    • ● 5.1黎曼积分的局限性, 勒贝格积分简介
      • ● 5.1.1Riemann 积分的局限性
      • ● 5.1.2Lebesgue 积分简介
    • ● 5.2非负简单函数的勒贝格积分
      • ● 5.2.1非负简单函数 Lebesgue 积分的定义与例子
      • ● 5.2.2非负简单函数 Lebesgue 积分的性质
    • ● 5.3非负可测函数的勒贝格积分
      • ● 5.3.1非负可测函数的 Lebesgue 积分的定义
      • ● 5.3.2非负可测函数 Lebesgue 积分的基本性质
      • ● 5.3.3非负可测函数 Lebesgue 积分的重要性质1: Levi 引理
      • ● 5.3.4非负可测函数 Lebesgue 积分的重要性质2: 逐项积分
      • ● 5.3.5非负可测函数 Lebesgue 积分的重要性质3: Fatou 引理
    • ● 5.4一般可测函数的勒贝格积分
      • ● 5.4.1一般可测函数 Lebesgue 积分的定义
      • ● 5.4.2一般可测函数 Lebesgue 积分的基本性质
      • ● 5.4.3一般可测函数 Lebesgue 积分的重要性质1:函数可积等价于其绝对值可积
      • ● 5.4.4一般可测函数 Lebesgue 积分的重要性质2:绝对连续性
      • ● 5.4.5一般可测函数 Lebesgue 积分的重要性质3:Lebesgue控制收敛及其推论
      • ● 5.4.6应用: Lebesgue 可积函数的连续函数逼近
    • ● 5.5黎曼积分和勒贝格积分
      • ● 5.5.1回忆 Riemann 积分
      • ● 5.5.2连续函数的振幅刻画
      • ● 5.5.3Riemann 可积函数的刻画
      • ● 5..5.4Lebesgue 积分是 Riemann 积分的推广
      • ● 5.5.5Lebesgue 积分是非负 Riemann 反常积分的推广
      • ● 5.5.6Lebesgue 积分不是 Riemann 反常积分的推广
    • ● 5.6勒贝格积分的几何意义, 富比尼定理
      • ● 5.6.1直积与截面
      • ● 5.6.2降维法求测度: Fubini 定理的前奏
      • ● 5.6.3非负可测函数积分的几何意义
      • ● 5.6.4Fubini 定理与累次积分
    • ● 本章小结
  • 6微分与不定积分
    • ● 6.0引言
    • ● 6.1Vitali 定理
    • ● 6.2单调函数的可微性
    • ● 6.3有界变差函数
    • ● 6.4不定积分
      • ● 6.4.1不定积分及其性质
      • ● 6.4.2绝对连续函数及其性质
      • ● 6.4.3积分与微分为互逆运算 (Lebesgue 意义下)
      • ● 6.4.4AC 函数的进一步刻画
    • ● 6.5斯蒂尔切斯积分
    • ● 6.6L-S 测度与积分
    • ● 本章小结
  • 7度量空间和赋范线性空间
    • ● 泛函分析 (functional analysis) 绪论
    • ● 7.1度量空间的进一步例子
      • ● 7.1.1度量空间, 离散度量空间
      • ● 7.1.2更多的度量空间
    • ● 7.2度量空间中的极限, 稠密集, 可分空间
      • ● 7.2.1度量空间中的极限
      • ● 7.2.2度量空间中点列收敛的等价刻画
      • ● 7.2..3度量空间中的稠密子集, 可分空间
    • ● 7.3连续映射
      • ● 7.3.1连续映射的定义
      • ● 7.3.2连续映射的三个等价刻画
    • ● 7.4柯西点列和完备度量空间
      • ● 7.4.1Cauchy 点列
      • ● 7.4.2完备度量空间
      • ● 7.4.3完备度量空间的例子
      • ● 7.4.4不是完备度量空间的例子
    • ● 7.5度量空间的完备化
      • ● 7.5.1序言, 保距映射, 等距同构
      • ● 7.5.2度量空间的完备化
    • ● 7.6压缩映射原理及其应用
      • ● 7.6.1压缩映射原理
      • ● 7.6.2压缩映射原理的应用
    • ● 7.7线性空间
      • ● 7.7.1线性空间
      • ● 7.7.2线性空间的例子
      • ● 7.7.3线性空间的相关概念
    • ● 7.8赋范线性空间和巴拿赫空间
      • ● 7.8.1赋范线性空间和巴拿赫 (Banach) 空间
      • ● 7.8.2Banach 空间的例子
      • ● 7.8.3有限维赋范线性空间
  • 8有界线性算子和连续线性泛函
    • ● 8.1有界线性算子和连续线性泛函
      • ● 8.1.1线性算子和线性泛函的定义
      • ● 8.1.2线性算子和线性泛函的例子
      • ● 8.1.3有界线性算子和连续线性泛函
      • ● 8.1.4有界线性算子和连续线性泛函的例子
    • ● 8.2有界线性算子空间和共轭空间
      • ● 8.2.1有界线性算子全体所成空间
      • ● 8.2.2共轭空间
    • ● 8.3有限秩算子
      • ● 8.3.1有限秩算子
      • ● 8.3.2有限秩算子全体是 Banach 代数的一个理想
      • ● 8.3.3商空间
      • ● 8.3.4商空间的例子
      • ● 8.3.5通过商空间将映射化为单射来处理
      • ● 8.3.6闭值域的一个充分条件
      • ● 8.3.7恒等算子的有限秩扰动不改变值域的闭性
  • 9内积空间和希尔伯特空间
    • ● 9.0引论
    • ● 9.1内积空间的基本概念
      • ● 9.1.1内积空间的定义
      • ● 9.1.2内积空间与赋范线性空间的联系
      • ● 9.1.3内积空间的例子
    • ● 9.2投影定理
      • ● 9.2.1引言
      • ● 9.2.2极小化向量定理
      • ● 9.2.3内积空间中的正交, 极小化向量的性质
      • ● 9.2.4线性空间中的代数补子空间 (直和)
      • ● 9.2.5内积空间中的正交补子空间
      • ● 9.2.6Hilbert 空间中的正交分解
    • ● 9.3希尔伯特空间中的规范正交基
      • ● 9.3.1引论
      • ● 9.3.2正交系
      • ● 9.3.3内积空间中的 Fourier 系数
      • ● 9.3.4内积空间中的 Bessel 不等式、Parseval 等式、Riemann-Lebesgue 引理
      • ● 9.3.5抽象空间中的级数论
      • ● 9.3.6内积空间中的规范正交系的完全性
      • ● 9.3.7Hilbert 空间中完全规范正交系的存在性、Hilbert 维数
    • ● 9.4希尔伯特空间上的连续线性泛函
      • ● 9.4.1Riesz 表示定理
      • ● 9.4.2Hilbert 空间中的共轭算子
    • ● 9.5自伴算子、酉算子和正规算子
      • ● 9.5.1引论
      • ● 9.5.2Hilbert 空间的自伴算子, 正规算子和酉算子
      • ● 9.5.3各算子间的关系
      • ● 9.5.4复内积空间中有界线性算子为零的充要条件
      • ● 9.5.5自伴算子的性质
      • ● 9.5.6酉算子的性质
      • ● 9.5.7正规算子的性质
  • Banach 空间中的基本定理
    • ● 本章主要讨论泛函分析的四大基本定理
    • ● 泛函延拓定理
    • ● $C[a,b]$ 的共轭空间
    • ● 共轭算子
    • ● 纲定理和一致有界性定理
    • ● 强收敛, 弱收敛和一致收敛
    • ● 逆算子定理
    • ● 闭图像定理
  • 作业及视频讲解
    • ● 1.1 集合的表示
    • ● 1.2 集合的运算
    • ● 1.3 对等与基数
    • ● 1.4 可数集合
    • ● 1.5 不可数集合
    • ● 2.1 度量空间,   n 维欧氏空间
    • ● 2.2 聚点, 内点, 完备集
    • ● 2.3 开集, 闭集, 完备集
    • ● 2.4 直线上的开集, 闭集及完备集的构造
    • ● 2.5 Cantor 三分集
    • ● 3.1 外测度
    • ● 3.2 可测集
    • ● 3.3 可测集类
    • ● 3.4 总复习题
    • ● 4.1 可测函数及其性质
    • ● 4.2 Egrov 定理
    • ● 4.3 可测函数的构造
    • ● 4.4 依测度收敛
    • ● 5.3 非负可测函数的 Lebesgue 积分
    • ● 5.4 一般可测函数的 Lebesgue 积分
    • ● 5.5 Riemann 积分和 Lebesgue 积分
    • ● 5.6 Lebesgue 积分的几何意义, Fubini 定理
    • ● 6.1 Vitali 定理 6.2 单调函数的可微性 6.3 有界变差函数 6.4 不定积分
    • ● 7.1 度量空间的进一步例子
    • ● 7.2 度量空间中的极限, 稠密集, 可分空间
    • ● 7.3 连续映射
    • ● 7.4 柯西 (Cauchy) 点列和完备度量空间
    • ● 7.5 度量空间的完备化
    • ● 7.6 压缩映射原理及其应用
    • ● 7.7 线性空间
    • ● 7.8 赋范线性空间和巴拿赫 (Banach) 空间
    • ● 8.1 有界线性算子和连续线性泛函
    • ● 8.2 有界线性算子空间和共轭空间
    • ● 8.3 有限秩算子
    • ● 9.1 内积空间的基本概念
    • ● 9.2 投影定理
    • ● 9.3 希尔伯特空间中的规范正交基
    • ● 9.4 希尔伯特空间上的连续线性泛函
    • ● 9.5 自伴算子、酉算子和正常算子
0.3构造 Lebesgue 积分-实变函数

构造 Lebesgue 积分-实变函数

Lebesgue (18750628-19410726, France)

实变函数的开创者 Lebesgue (勒贝格) 之传记 |

1、 Riemann 积分是对定义域进行分划, Lebesgue 积分则是对值域进行分划 (条条大路通罗马, 这条路更艰辛, 但风景这边独好): 当    (  表示远远小于) 时,

极限存在不? 存在的话, 就是 Lebesgue 积分!  同样是求面积, 方法不同. 浅显的说, 要数一堆面值为    毛和    元的硬币总额, Riemann 积分的思想是 一个个拿过来相加, 而 Lebesgue 积分的思想是 先将硬币整理, 面值相同的堆在一起.  

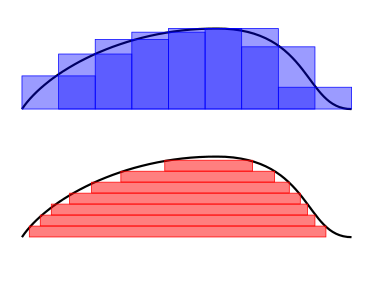
上面是 Riemann 积分的思想, 下面是 Lebesgue 积分的思想

宋诗也有云:  

2、 路很艰辛, 但还是要走 (路虽远, 不行不至; 事虽难, 不为不成)! 现在的问题是如何求    的长度. 先看个例子: 对 Dirichlet 函数而言,

那么 无理数的长度 和 有理数的长度 是多少呢?  我们将在第三章中将以前所学 长度 推广为 测度 measure, 而可定义诸多集合的测度. 更多的集合可以求面积啦.

3、 本书结构如下. 还有泛函分析呢. 这个等我们学完实变函数再说吧. 不然说了又忘记了.    

小作业: 总结下你自大学以来学过的空间 (比如线性空间, 群, 环, 域).