2.7  常用的数学函数

     前面介绍了几个常用的输入/输出函数。除了这些函数外，C语言还提供了许多具有不同功能的基本函数，比较常用的是数学函数，使用这些函数可以进行一些基本的数学运算。

     在使用数学函数之前，要求在程序开头包含头文件 math.h，

     即    #include <math.h>

     以下函数的参数类型和函数值类型均为实型：

      sqrt( x )     求x的平方根，x≥0

      pow(x,y)    求

      exp(x)       求 

      abs(x)      求x的绝对值，x为int型数。

      fabs(x)     求x的绝对值，x为 double型浮点数。

      log(x)        求x的对数，以e为底，x>0

      log10(x)    求x的对数，以10为底，x>0

      sin(x)        求x的正弦，x的单位为弧度。

      cos(x)        求x的余弦，x的单位为弧度。

      tan(x)         求x的正切，x的单位为弧度。

   度(d) --> 弧度(a)   a=pi*d/180

      rand( )       产生0~32767范围内的随机整数。

例2-14   输入一个正数x，求x的平方根。

1. #include   <stdio.h>

2. #include   <math.h>

3. main()

4. {   float x;   double  y;

5.     printf("input x:");

6.     scanf("%f", &x );

7.     y= sqrt( x );

8.     printf("sqrt(%-7.2f)=%7.2f  \n", x, y);

9. }

运行程序的结果如图2-12所示。

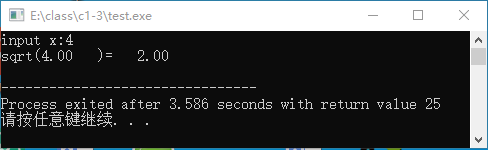
图2-12  例2-14运行结果

其中，格式符“%-7.2f”中的“-”号表示输出格式为左对齐。

例2-15   使用pow()函数求幂函数    。

1. #include <stdio.h>

2. #include <math.h>

3. main()

4. {   float a, b;   double y;

5.    printf("a=");    scanf("%f", &a );

6.    printf("b=");     scanf("%f", &b );

7.    y=pow(a, b);

8.    printf("a=%.1f, b=%.1f, a^b =%.1f\n", a, b, y );

9. }

运行上面的程序，输出结果如图2-13所示。

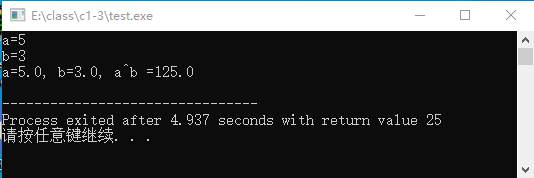
例2-16    使用pow()函数求平方根或立方根

源程序如下：

1.  #include  <stdio.h>

2. #include   <math.h>

3. main()

4. {     double   k, j;

5.       k=25;

6.       j=1.0 / 2;

7.       printf("%f, %f, %f \n", pow(k, j), sqrt(k), pow(k, 1/3.0));

8. }

 运行结果如图2-14所示。

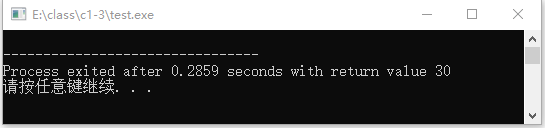
图2-14  例2-16运行结果

由例2-16可知，可利用pow()函数求某非负数的平方根或立方根。注意上面的语句:

 不能写成:

 j=1/2;

 这是因为“j=1/2”为两个整数相除，结果为整数0。应该使用以下格式：

 pow(x,0.5)   或pow(x,1.0/2)   或pow(x,1/2.0)

例2-17  三角函数的应用。

 使用三角函数时，若给定的是角度值x，则应转换为弧度 x*PI/180，其中PI为圆周率，x为实数。

源程序如下： 

1. #include <stdio.h>

2.  #include <math.h>

3.  #define PI    3.1415926

4.  main()

5. {    float x, alfa;

6.      printf("输入一个角度数:    ");

7.      scanf("%f", &x);

8.      alfa = x*PI/180;

9.      printf("弧度数为: %7.1f, 正弦函数sin(%7.1f)=%7.1f\n",alfa, alfa, sin(alfa));

10.  }

该程序运行结果如图2-15所示。

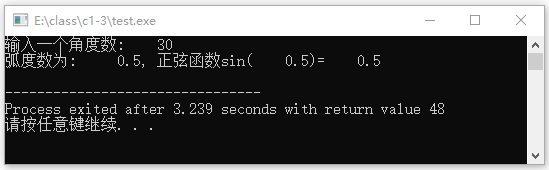
图2-15   例2-17运行结果

例2-18    计算一元二次方程的根

程序分析：

计算一元二次方程的根，相关数学公式如下：

测试案例：计算方程的根

          从键盘上输入:1,-2,-3；期望结果：x1=3，x2=-1

源程序如下：

1. #include    <stdio.h>

2. #include    <math.h>

3. main( )

4. {     float a, b, c, dlta;   double x1,   x2;

5.       scanf("%f,%f,%f", &a, &b, &c);

6.       dlta=b*b-4 * a * c;

7.       x1 = (-b + sqrt(dlta)) /( 2*a);

8.       x2 = (-b - sqrt(dlta)) /(2*a);

9.       printf("x1=%f, x2=%f\n", x1, x2);

10. }

 运行结果如图2-16所示。

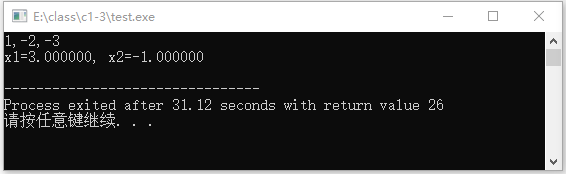
图2-16  例2-18运行结果

从以上程序运行结果分析，符合预期结果，从而验证程序正确。